9.3: Perimeter and Area
( \newcommand{\kernel}{\mathrm{null}\,}\)
Perimeter and area are two important and fundamental mathematical topics. They help you to quantify physical space and also provide a foundation for more advanced mathematics found in algebra, trigonometry, and calculus. Perimeter is a measurement of the distance around a shape and area gives us an idea of how much surface the shape covers.
Knowledge of area and perimeter is applied practically by people on a daily basis, such as architects, engineers, and graphic designers, and is math that is very much needed by people in general. Understanding how much space you have and learning how to fit shapes together exactly will help you when you paint a room, buy a home, remodel a kitchen, or build a deck.
The perimeter of a polygon is the sum of the lengths of tthe sides of the polygon.
The area is a measure of the amount of surface that polygon covers.
Find the perimeter of the given figure. All measurements indicated are inches.
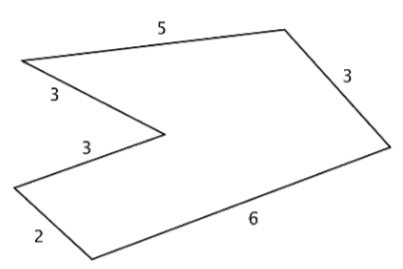
Solution
Since all the sides are measured in inches, just add the lengths of all six sides to get the perimeter.
Remember to include units.
Answer:
Find the perimeter of a triangle with sides measuring 6 cm, 8 cm, and 12 cm.
Solution
Since all the sides are measured in centimeters, just add the lengths of all three sides to get the perimeter.
Answer:
If a rectangle has length
A rectangle has a length of 8 centimeters and a width of 3 centimeters. Find the perimeter.
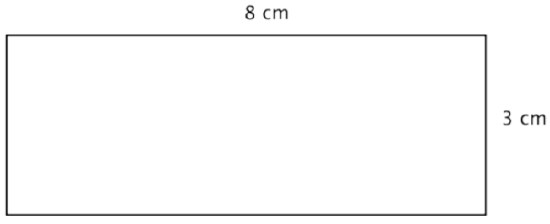
Solution
Since this is a rectangle, the opposite sides have the same lengths, 3 cm. and 8 cm. Add up the lengths of all four sides to find the perimeter.
Answer
Area of Parallelograms
The area of a two-dimensional figure describes the amount of surface the shape covers. You measure area in square units of a fixed size. Examples of square units of measure are square inches, square centimeters, or square miles. When finding the area of a polygon, you count how many squares of a certain size will cover the region inside the polygon.
Let’s look at a 4 x 4 square.
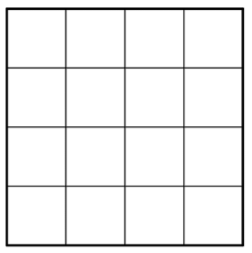
You can count that there are 16 squares, so the area is 16 square units. Counting out 16 squares doesn’t take too long, but what about finding the area if this is a larger square or the units are smaller? It could take a long time to count.
Fortunately, you can use multiplication. Since there are 4 rows of 4 squares, you can multiply
You can write “
To help you find the area of the many different categories of polygons, mathematicians have developed formulas. These formulas help you find the measurement more quickly than by simply counting. The formulas you are going to look at are all developed from the understanding that you are counting the number of square units inside the polygon. Let’s look at a rectangle.
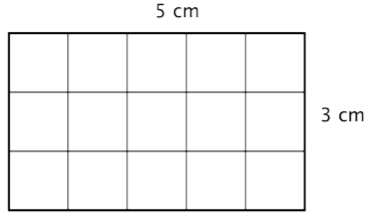
You can count the squares individually, but it is much easier to multiply 3 times 5 to find the number more quickly.
If a rectangle has length
A rectangle has a length of 8 centimeters and a width of 3 centimeters. Find the area.
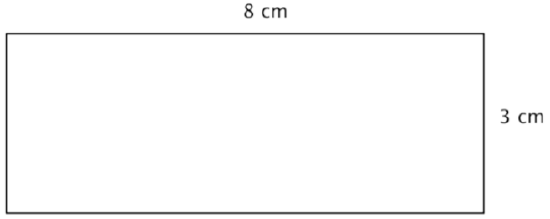
Solution
Start with the formula for the area of a rectangle, which multiplies the length times the width.
Substitute 8 for the length and 3 for the width.
Be sure to include the units, in this case, square cm.
Answer:
The formula for the area of any parallelogram (remember, a rectangle is a type of parallelogram) is the same as that of a rectangle:
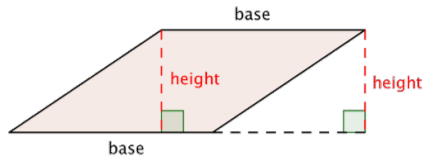
Find the area of the parallelogram.
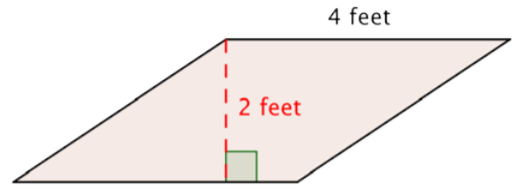
Solution
Start with the formula for the area of a parallelogram:
Substitute the values into the formula.
Multiply.
Answer: The area of the parallelogram is
Find the area of a parallelogram with a height of 12 feet and a base of 9 feet.
- Answer
-
The area of the parallelogram is
The formula for the area of a triangle can be explained by looking at a right triangle. Look at the image below—a rectangle with the same height and base as the original triangle. The area of the triangle is one half of the rectangle!
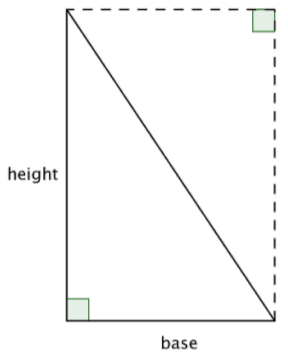
Since the area of two congruent triangles is the same as the area of a rectangle, you can come up with the formula
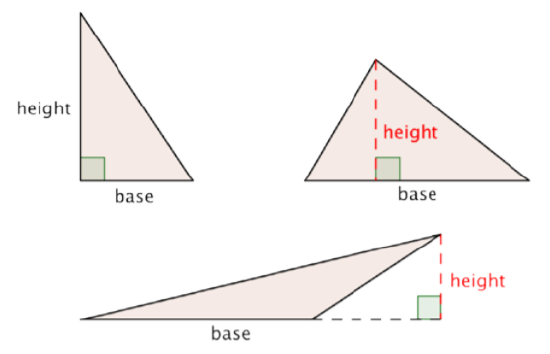
When you use the formula for a triangle to find its area, it is important to identify a base and its corresponding height, which is perpendicular to the base.
A triangle has a height of 4 inches and a base of 10 inches. Find the area.
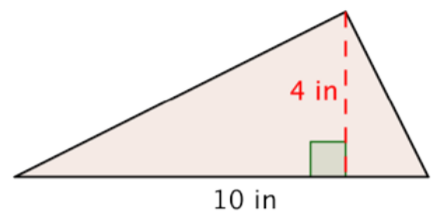
Solution
Start with the formula for the area of a triangle.
Substitute 10 for the base and 4 for the height.
Multiply.
Answer:
To find the area of a trapezoid, take the average length of the two parallel bases and multiply that length by the height:
Find the area of the trapezoid.
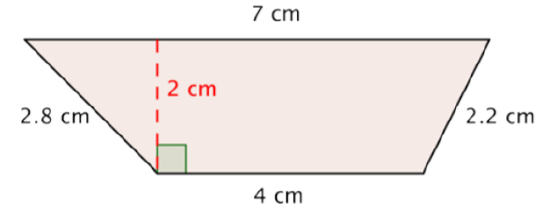
Solution
Start with the formula for the area of a trapezoid.
Substitute 4 and 7 for the bases and 2 for the height, and find A.
Answer: The area of the trapezoid is
Use the following formulas to find the areas of different shapes.
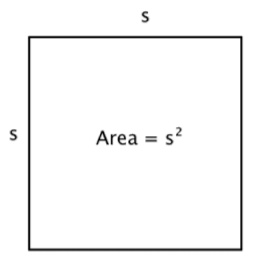
square:
rectangle:
parallelogram:
triangle:
trapezoid:
Circles are a common shape. You see them all over—wheels on a car, Frisbees passing through the air, compact discs delivering data. These are all circles.
A circle represents a set of points, all of which are the same distance away from a fixed, middle point. This fixed point is called the center. The distance from the center of the circle to any point on the circle is called the radius. The diameter is twice the radius.
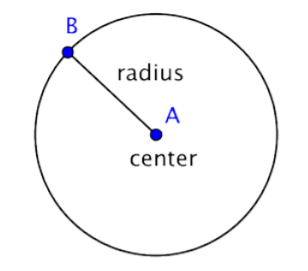
The distance around a circle is called the circumference. (Recall, the distance around a polygon is the perimeter.)
One interesting property about circles is that the ratio of a circle’s circumference and its diameter is the same for all circles. No matter the size of the circle, the ratio of the circumference and diameter will be the same. The ratio
The circumference
Find the circumference of a circle with a radius of 2.5 yards.
Solution
To calculate the circumference of a circle given a radius of 2.5 yards, use the formula
Answer: The circumference is
The area
Find the area of the circle.
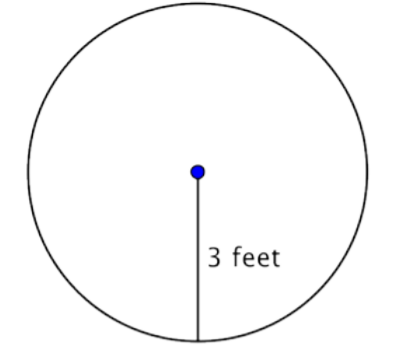
Solution
To find the area of this circle, use the formula
Answer The area is
A long time ago, a Greek mathematician named Pythagoras discovered an interesting property about right triangles: the sum of the squares of the lengths of each of the triangle’s legs is the same as the square of the length of the triangle’s hypotenuse. This property—which has many applications in science, art, engineering, and architecture—is now called the Pythagorean Theorem.
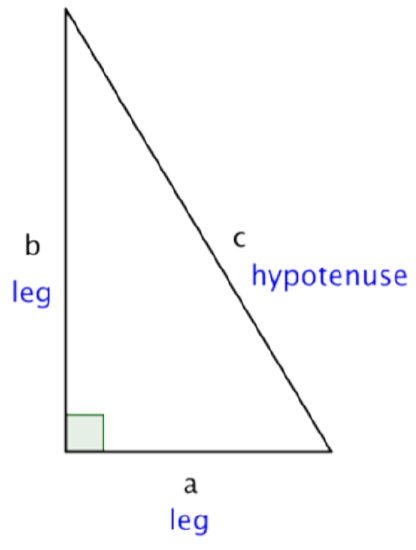
If a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse, then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
This relationship is represented by the formula:
When you see the equation
Let’s try out all of the Pythagorean Theorem with an actual right triangle.
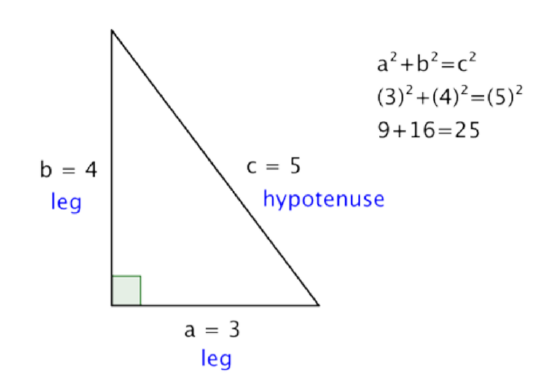
This theorem holds true for this right triangle—the sum of the squares of the lengths of both legs is the same as the square of the length of the hypotenuse. And, in fact, it holds true for all right triangles.
The Pythagorean Theorem can also be represented in terms of area. In any right triangle, the area of the square drawn from the hypotenuse is equal to the sum of the areas of the squares that are drawn from the two legs. You can see this illustrated below in the same 3-4-5 right triangle.
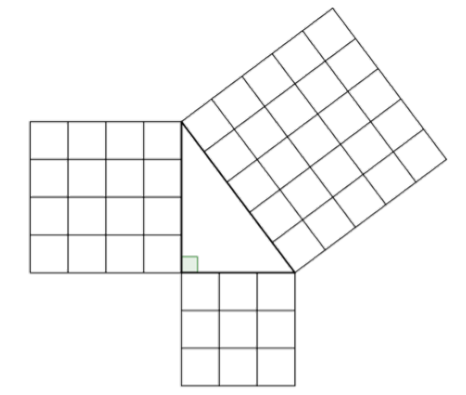
Note that the Pythagorean Theorem only works with right triangles.
Find the missing length
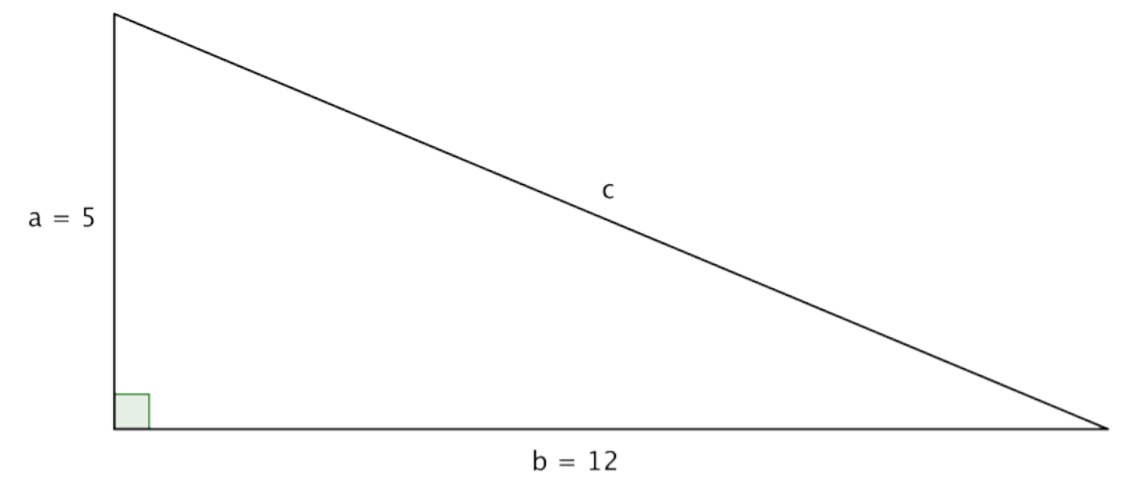
Solution
In the triangle above, you are given measures for legs a and b: 5 and 12, respectively. You can use the Pythagorean Theorem to find a value for the length of c, the hypotenuse.
The Pythagorean Theorem.
Substitute known values for a and b.
Evaluate.
Simplify. To find the value of c, think about a number that, when multiplied by itself, equals 169. Does 10 work? How about 11? 12? 13? (You can use a calculator to multiply if the numbers are unfamiliar.)
The square root of 169 is 13.
Using the formula, you find that the length of c, the hypotenuse, is 13.
Find the length of side a in the triangle below. Use a calculator to estimate the square root to one decimal place.
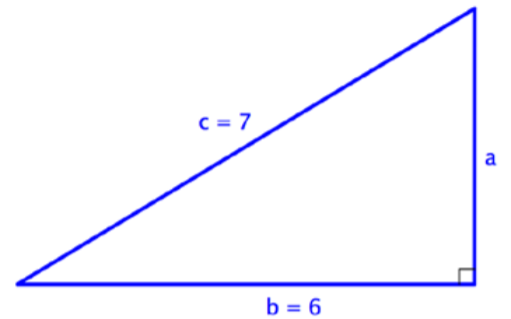
Solution
In this right triangle, you are given the measurements for the hypotenuse, c, and one leg, b. The hypotenuse is always opposite the right angle and it is always the longest side of the triangle.
To find the length of leg a, substitute the known values into the Pythagorean Theorem.
Solve for
Use a calculator to find the square root of 13. The calculator gives an answer of 3.6055…, which you can round to 3.6. (Since you are approximating, you use the symbol ≈.)
Answer: a ≈ 3.6


