9.2: Polygons
- Page ID
- 83176
A polygon is a closed plane figure with three or more straight sides called edges. An endpoint of an edge a vertex. A polygon is regular if all of its edges are the same length and all of its angles have the same measure.
Polygons each have a special name based on the number of sides they have. For example, the polygon with three sides is called a triangle because “tri” is a prefix that means “three.” Its name also indicates that this polygon has three angles. The prefix “poly” means many.
The smallest polygon you can have is a triangle, which has three sides. The table below shows and describes three classifications of triangles. Notice how the types of angles in the triangle are used to classify the triangle.
| Name of Triangle | Picture of Triangle | Description |
| Acute Triangle |  |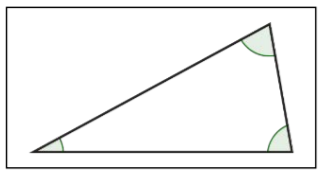
A triangle with 3 acute angles (3 angles measuring between 0° and 90°). |
| Obtuse Triangle |  |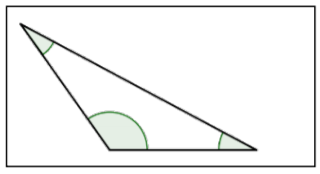
A triangle with 1 obtuse angle (1 angle measuring between 90° and 180°). |
| Right Triangle |  |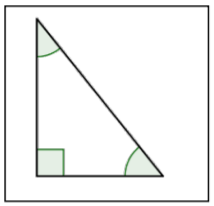
A triangle containing one right angle (1 angle that measures 90°). Note that the right angle is shown with a corner mark and does not need to be labeled 90°. |
The sum of the measures of the three interior angles of a triangle is always 180°.
This fact can be applied to find the measure of the third angle of a triangle, if you are given the other two.
A triangle has two angles that measure 35° and 75°. Find the measure of the third angle.
Solution
The sum of the three interior angles of a triangle is 180°.
35° + 75° + \(x\) = 180°
Find the value of \(x\).
110º + \(x\) = 180º
\(x\) = 180° ‒ 110º
\(x\) = 70°
Answer: The third angle of the triangle measures 70°.
One of the angles in a right triangle measures 57º. Find the measurement of the third angle.
Solution
The sum of the three angles of a triangle is 180°. One of the angles has a measure of 90° as it is a right triangle.
57° + 90° + \(x\) = 180°
Simplify.
147º + \(x\) = 180°
Find the value of \(x\).
\(x\) = 180º - 147º
\(x\) = 33º
Answer: The third angle of the right triangle measures 33°.
There is an established convention for naming triangles. The labels of the vertices of the triangle, which are generally capital letters, are used to name a triangle.
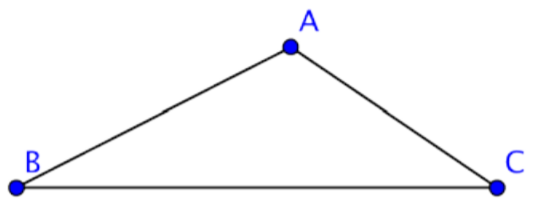
You can call this triangle ABC or ∆ABC since A, B, and C are vertices of the triangle. When naming the triangle, you can begin with any vertex. Then keep the letters in order as you go around the polygon. The triangle above could be named in a variety of ways: ∆ABC, or ∆CBA. The sides of the triangle are line segments AB, AC, and CB.
Just as triangles can be classified as acute, obtuse, or right based on their angles, they can also be classified by the length of their sides. Sides of equal length are called congruent sides. While we designate a segment joining points A and B by the notation \(\overline{AB}\), we designate the length of a segment joining points A and B by the notation AB without a segment bar over it. The length AB is a number, and the segment \(\overline{AB}\) is the collection of points that make up the segment.
Mathematicians show congruency by putting a hash mark symbol through the middle of sides of equal length. If the hash mark is the same on one or more sides, then those sides are congruent. If the sides have different hash marks, they are not congruent. The table below shows the classification of triangles by their side lengths.
| Name of Triangle | Picture of Triangle | Description |
| Equilateral Triangle |  |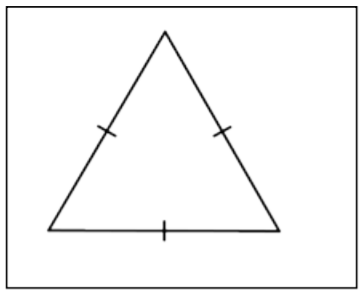
A triangle whose three sides have the same length. These sides of equal length are called congruent sides. |
| Isosceles Triangle |  |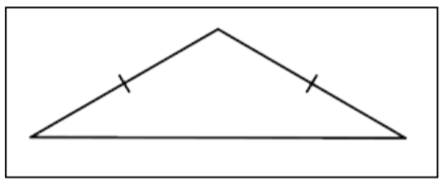
A triangle with exactly two congruent sides. |
| Scalene Triangle |  |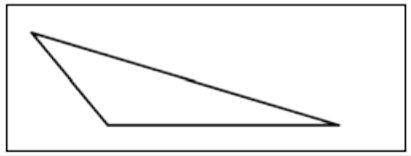
A triangle in which all three sides are a different length. |
To describe a triangle even more specifically, you can use information about both its sides and its angles.
Classify the triangle below.
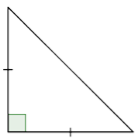
Solution
Notice what kind of angles the triangle has. Since one angle is a right angle, this is a right triangle.
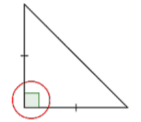
Notice the lengths of the sides. Are there congruence marks or other labels?
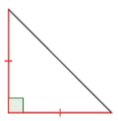
The congruence marks tell us there are two sides of equal length. So, this is an isosceles triangle.
Answer: This is an isosceles right triangle
Quadrilaterals are polygons with exactly four side.
The sum of the interior angles of any quadrilateral is 360°.
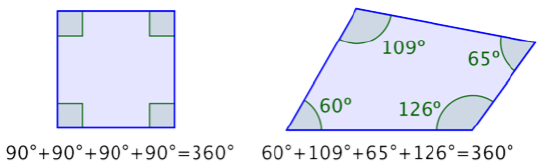
You can also use your knowledge of triangles as a way to understand why the sum of the interior angles of any quadrilateral is 360°. Any quadrilateral can be divided into two triangles as shown in the images below.
In the first image, the quadrilaterals have each been divided into two triangles. The angle measurements of one triangle are shown for each.
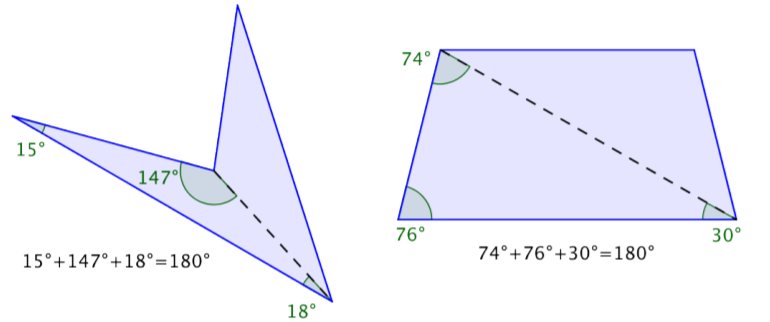
These measurements add up to 180º. Now look at the measurements for the other triangles—they also add up to 180º!
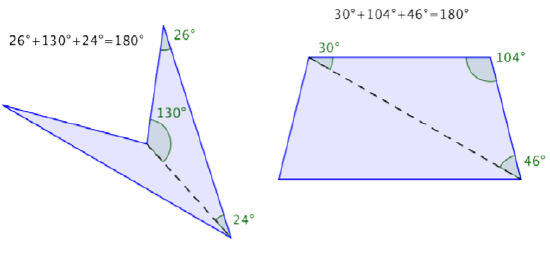
Since the sum of the interior angles of any triangle is 180° and there are two triangles in a quadrilateral, the sum of the angles for each quadrilateral is 360°.
Let’s start by examining the group of quadrilaterals that have two pairs of parallel sides. These quadrilaterals are called parallelograms. They take a variety of shapes, but one classic example is shown below.
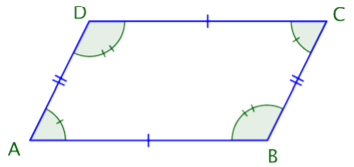
Imagine extending the pairs of opposite sides. They would never intersect because they are parallel. Notice, also, that the opposite angles of a parallelogram are congruent, as are the opposite sides. (Remember that “congruent” means “the same size.”) The geometric symbol for congruent is \(≅\), so you can write ∠A ≅ ∠C and ∠B ≅ ∠D. The parallel sides are also the same length: \(\overline{AB} ≅ \overline{DC}\) and \(\overline{BC} ≅ \overline{AD}\). These relationships are true for all parallelograms.
There are two special cases of parallelograms that will be familiar to you from your earliest experiences with geometric shapes. The first special case is called a rectangle. By definition, a rectangle is a parallelogram because its pairs of opposite sides are parallel. A rectangle also has the special characteristic that all of its angles are right angles; all four of its angles are congruent.
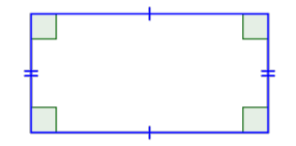
The other special case of a parallelogram is a special type of rectangle, a square. A square is one of the most basic geometric shapes. It is a special case of a parallelogram that has four congruent sides and four right angles.
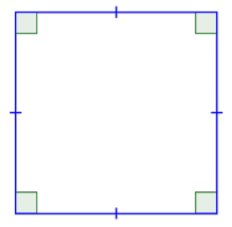
A square is also a rectangle because it has two sets of parallel sides and four right angles. A square is also a parallelogram because its opposite sides are parallel. So, a square can be classified in any of these three ways, with “parallelogram” being the least specific description and “square,” the most descriptive.
Another quadrilateral that you might see is called a rhombus. All four sides of a rhombus are congruent. Its properties include that each pair of opposite sides is parallel, also making it a parallelogram.
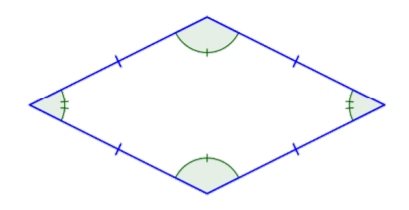
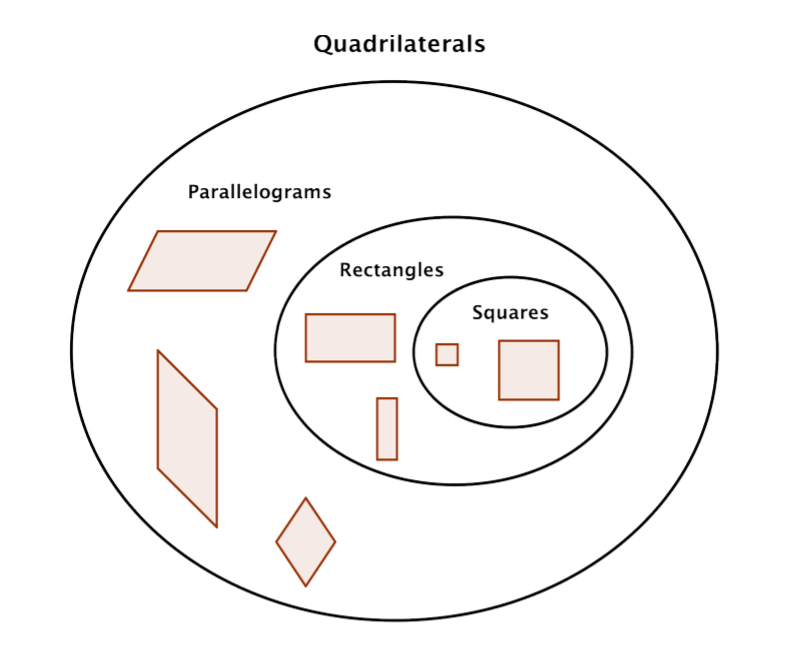
In summary, all squares are rectangles, but not all rectangles are squares. All rectangles are parallelograms, but not all parallelograms are rectangles. And all of these shapes are quadrilaterals.
The diagram below illustrates the relationship between the different types of quadrilaterals.
There is another special type of quadrilateral. This quadrilateral has the property of having only one pair of opposite sides that are parallel. Here is one example of a trapezoid.
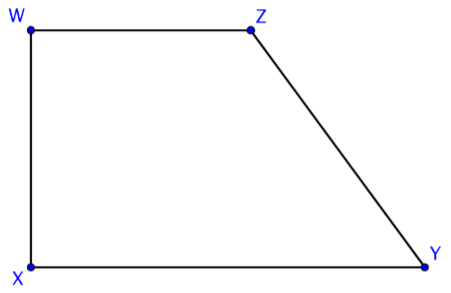
Notice that \(\overline{XY} || \overline{WZ}\), and that \(\overline{WX}\) and \(\overline{ZY}\) are not parallel. You can easily imagine that if you extended sides \(\overline{WX}\) and \(\overline{ZY}\), they would intersect above the figure.
If the non-parallel sides of a trapezoid are congruent, the trapezoid is called an isosceles trapezoid. Like the similarly named triangle that has two sides of equal length, the isosceles trapezoid has a pair of opposite sides of equal length. The other pair of opposite sides is parallel. Below is an example of an isosceles trapezoid.
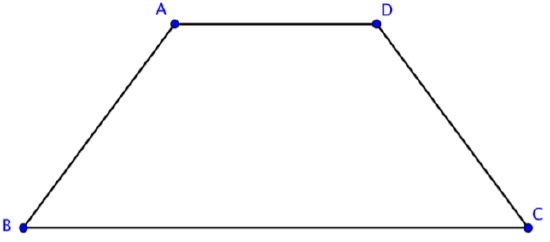
In this trapezoid ABCD, \(\overline{BC} || \overline{AD}\) and \(\overline{AB} ≅ \overline{CD}\).
Determine the measures of ∠M and ∠L.
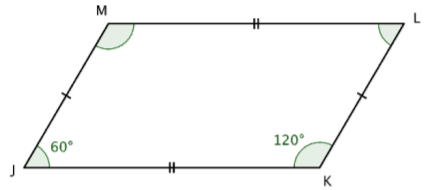
Solution
Identify opposite angles.
∠L is opposite ∠J
∠M is opposite ∠K
A property of parallelograms is that opposite angles are congruent.
∠L ≅ ∠J
∠M ≅ ∠K
Use the given angle measurements to determine measures of opposite angles.
m∠J = 60°, so m∠L = 60°
m∠K = 120°, so m∠M = 120°
Answer: m∠L = 60° and m∠M = 120°
The table below summarizes the special types of quadrilaterals and some of their properties.
| Name of Quadrilateral | Quadrilateral | Description |
|
Parallelogram |
 |
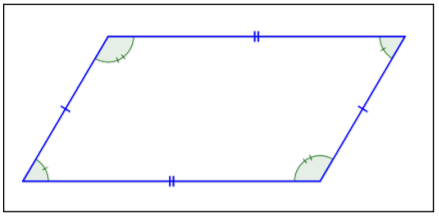2 pairs of parallel sides. Opposite sides and opposite angles are congruent. |
|
Rectangle |
 |
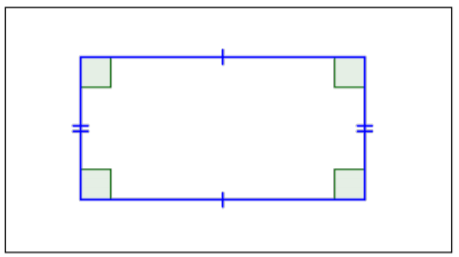2 pairs of parallel sides. 4 right angles (90°). Opposite sides are parallel and congruent. All angles are congruent. |
|
Square |
 |
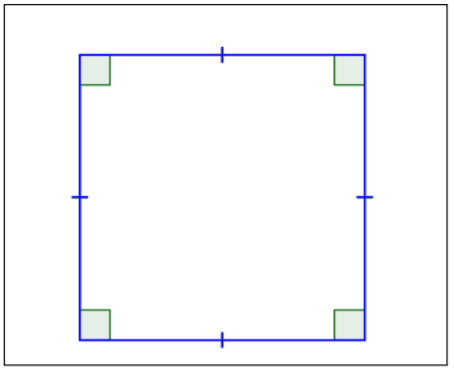4 congruent sides. 4 right angles (90°). Opposite sides are parallel. All angles are congruent. |
|
Trapezoid |
 |
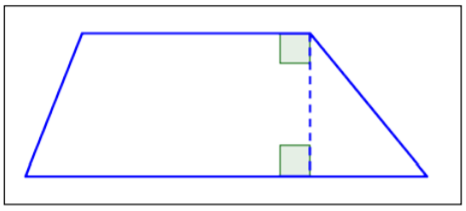Only one pair of opposite sides is parallel. |
The sum of the measures of the interior angles of a polygon having n sides is \((n-2)\times 180^{\circ}\).
If the polygon is a regular polygon, then each interior angle is \(\frac{(n-2)\times 180^{\circ}}{n}\)
What is the measure of an interior angle of a regular 12-sided polygon (dodecagon)?
Solution
Since the polygon is regular, each interior angle will have the same measure of \(\frac{(12-2)\times 180^{\circ}}{12}\) = 150°
Two polygons are similar if their corresponding sides are proportional and their corresponding angles are equal.
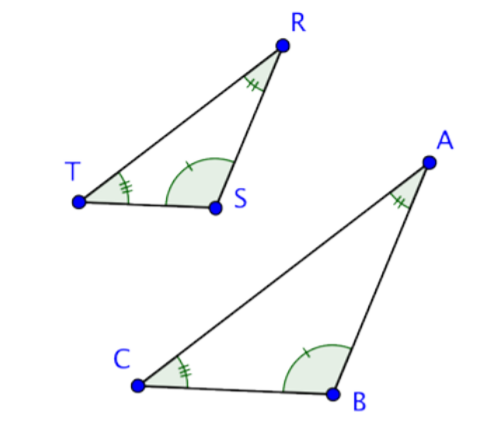OR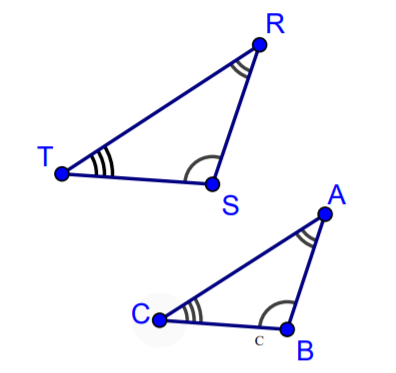 
\( \frac{\overline{AB}}{\overline{RS}} = \frac{\overline{BC}}{\overline{ST}} = \frac{\overline{AC}}{\overline{RT}} \)
∠A \(≅\) ∠R, ∠B \(≅\) ∠S, and ∠C \(≅\) ∠T
This extends to all polygons and not just triangles.
Determine if the triangles below are similar by seeing if their corresponding sides are proportional.
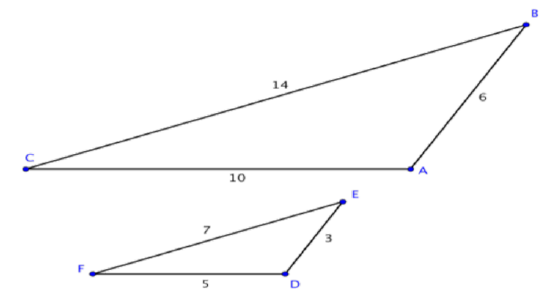
Solution
First determine the corresponding sides, which are opposite corresponding angles.
\(\overline{CA}\) ↔ \(\overline{FD}\)
\(\overline{AB}\) ↔ \(\overline{DE}\)
\(\overline{BC}\) ↔ \(\overline{EF}\)
Write the corresponding side lengths as ratios.
\( \frac{\overline{CA}}{\overline{FD}} = \frac{\overline{AB}}{\overline{DE}} = \frac{\overline{BC}}{\overline{EF}} \)
Substitute the side lengths into the ratios, and determine if the ratios of the corresponding sides are equivalent. They are, so the triangles are similar.
\( \frac{10}{5} = \frac{6}{3} = \frac{14}{7} \)
\(2 = 2 = 2\)
Answer: ∆ABC and ∆DEF are similar.
The mathematical symbol ~ means “is similar to”. So, you can write ∆ABC is similar to ∆DEF as ∆ABC ~ ∆DEF.
∆ABC and ∆XYZ are similar triangles. What is the length of side BC?
Solution
In similar triangles, the ratios of corresponding sides are proportional. Set up a proportion of two ratios, one that includes the missing side.
\(\frac{BC}{YZ} = \frac{AB}{XY}\)
Substitute in the known side lengths for the side names in the ratio. Let the unknown side length be n.
\(\frac{n}{2} = \frac{6}{1.5}\)
Solve for n using cross multiplication.
\(2 \cdot 6 = 1.5 \cdot n\)
\(12 = 1.5n\)
\(8 = n\)
Applying knowledge of triangles, similarity, and congruence can be very useful for solving problems in real life. Just as you can solve for missing lengths of a triangle drawn on a page, you can use triangles to find unknown distances between locations or objects.
When the sun is at a certain angle in the sky, a 6-foot tree will cast a 4-foot shadow. How tall is a tree that casts an 8-foot shadow?
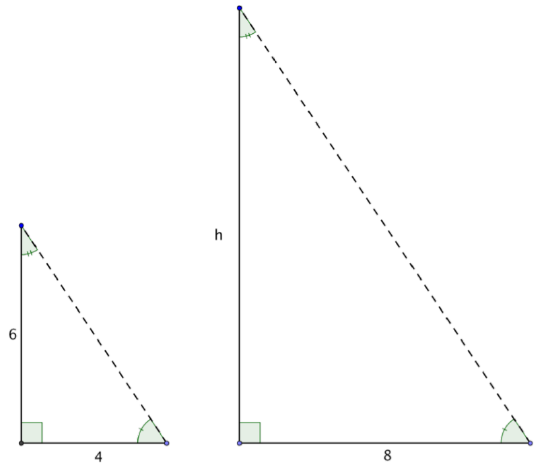
Solution
The angle measurements are the same, so the triangles are similar triangles. Since they are similar triangles, you can use proportions to find the size of the missing side.
\(\frac{\text{Tree 1}}{\text{Tree 2}} = \frac{\text{Shadow 1}}{\text{Shadow 2}}\)
Set up a proportion comparing the heights of the trees and the lengths of their shadows.
Substitute in the known lengths. Call the missing tree height h.
\(\frac{6}{h} = \frac{4}{8}\)
Solve for h using cross-multiplication.
\(6 \cdot 8 = 4h\)
\(48 = 4h\)
\(12 = h\)
Answer: The tree is 12 feet tall.