2.3: Volume of Geometric Solids

Last updated
Save as PDF

Page ID: 109871

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Identify geometric solids.
Find the volume of geometric solids.
Find the volume of a composite geometric solid.

Introduction

Living in a two-dimensional world would be pretty boring. Thankfully, all of the physical objects that you see and use every day—computers, phones, cars, shoes—exist in three dimensions. They all have length, width, and height. (Even very thin objects like a piece of paper are threedimensional. The thickness of a piece of paper may be a fraction of a millimeter, but it does exist.)

In the world of geometry, it is common to see three-dimensional figures. In mathematics, a flat side of a three-dimensional figure is called a face. Polyhedrons are shapes that have four or more faces, each one being a polygon. These include cubes, prisms, and pyramids. Sometimes you may even see single figures that are composites of two of these figures. Let’s take a look at some common polyhedrons.

Identifying Solids

The first set of solids contains rectangular bases. Have a look at the table below, which shows each figure in both solid and transparent form.

Name	Definition	Solid Form	Transparent Form
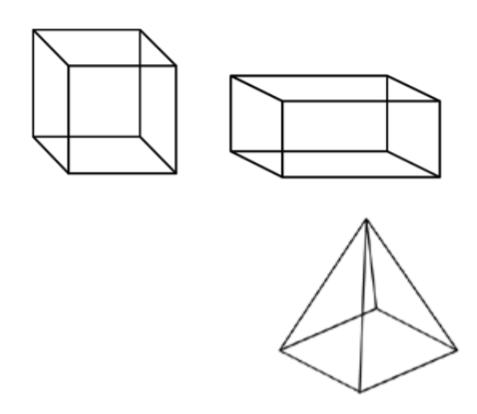
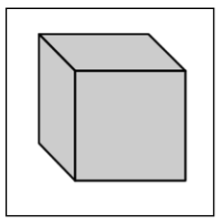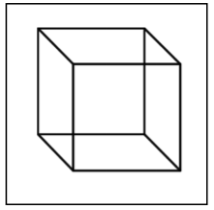Cube	A six-sided polyhedron that has congruent squares as faces.	$clipboard_e225881b438db4ecf6b003f26e618cff3.png$	$clipboard_e6ed907c23a2ed3217441eab4bc15e5a7.png$
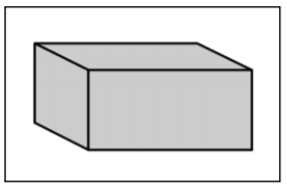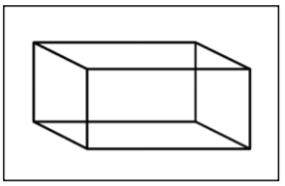Rectangular prism	A polyhedron that has three pairs of congruent, rectangular, parallel faces.	$clipboard_e9dbbb9a9a8f377a9a8cc93a696f291e2.png$	$clipboard_e470e718cdc8c0e59d200bfeaf62c1770.png$
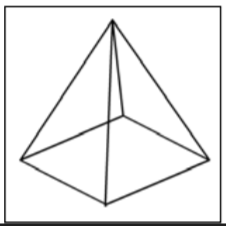Pyramid	A polyhedron with a polygonal base and a collection of triangular faces that meet at a point.	$clipboard_e6b058e3c3daf484d9b198b5fbae23cee.png$	$clipboard_e898a39a19a8fb7c8afbd30895f9e17f2.png$

Notice the different names that are used for these figures. A cube is different than a square, although they are sometimes confused with each other—a cube has three dimensions, while a square only has two. Likewise, you would describe a shoebox as a rectangular prism (not simply a rectangle), and the ancient pyramids of Egypt as…well, as pyramids (not triangles).

In this next set of solids, each figure has a circular base.

Name	Definition	Solid Form	Transparent Form
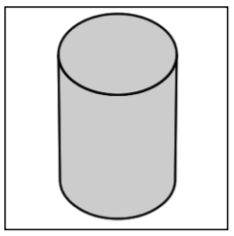
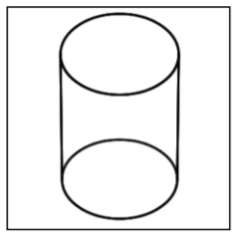
Cylinder	A solid figure with a pair of circular, parallel bases and a round, smooth face between them.	$clipboard_eec98fb61f9af0a10734644649685e8de.png$	$clipboard_ea6485c0a4c2eaacda9740cb92bcd41dd.png$
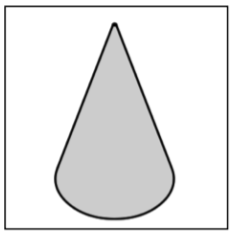
Cone	A solid figure with a single circular base and a round, smooth face that diminishes to a single point.	$clipboard_eae112320ec9d8be4cefba631f5ce4644.png$	$clipboard_ee55d8d9244e50706e72493b2e2dfc9c8.png$

Take a moment to compare a pyramid and a cone. Notice that a pyramid has a rectangular base and flat, triangular faces; a cone has a circular base and a smooth, rounded body.

Finally, let’s look at a shape that is unique: a sphere.

Name	Definition	Solid Form	Transparent Form
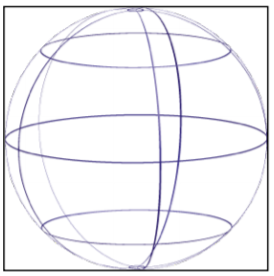Sphere	A solid, round figure where every point on the surface is the same distance from the center.	$clipboard_eb7348e12f04cc63cf41e53752e3f359c.png$	$clipboard_efbb88b3e293520d78e8e9acf8bd5b802.png$

There are many spherical objects all around you—soccer balls, tennis balls, and baseballs being three common items. While they may not be perfectly spherical, they are generally referred to as spheres.

Example $\PageIndex{1}$

A three-dimensional figure has the following properties:

It has a rectangular base.
It has four triangular faces.

What kind of a solid is it?

Solution

A rectangular base indicates that it must be a cube, rectangular prism, or pyramid.

$clipboard_e9c2230051ade57107d42bf26da5b63ef.png$

Since the faces are triangular, it must be a pyramid.

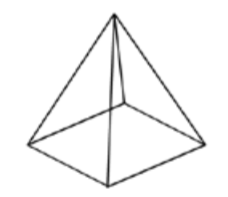
$clipboard_e894fb3858e172da03eacbeb6d1dc10ab.png$

Answer: The solid is a pyramid.

Volume

Recall that perimeter measures one dimension (length), and area measures two dimensions (length and width). To measure the amount of space a three-dimensional figure takes up, you use another measurement called volume.

To visualize what “volume” measures, look back at the transparent image of the rectangular prism mentioned earlier (or just think of an empty shoebox). Imagine stacking identical cubes inside that box so that there are no gaps between any of the cubes. Imagine filling up the entire box in this manner. If you counted the number of cubes that fit inside that rectangular prism, you would have its volume.

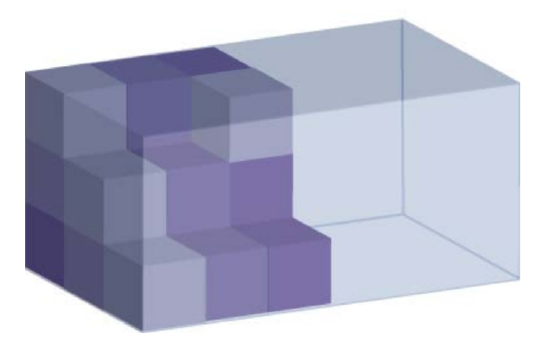
$clipboard_e4b1f1f400830085a1f317c250b539518.png$

Volume is measured in cubic units. The shoebox illustrated above may be measured in cubic inches (usually represented as $\text{in}^3$ or $\text{inches}^3$), while the Great Pyramid of Egypt would be more appropriately measured in cubic meters ($\text{m}^3$ or $\text{meters}^3$).

To find the volume of a geometric solid, you could create a transparent version of the solid, create a bunch of 1x1x1 cubes, and then stack them carefully inside. However, that would take a long time! A much easier way to find the volume is to become familiar with some geometric formulas and to use those instead.

Let’s go through the geometric solids once more and list the volume formula for each.

As you look through the list below, you may notice that some of the volume formulas look similar to their area formulas. To find the volume of a rectangular prism, you find the area of the base and then multiply that by the height.

Name	Transparent Form	Volume Formula
Cube	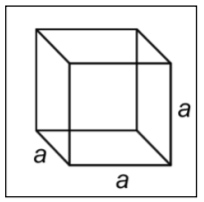$clipboard_e6ed98a1ec1dc95a879a6fddd3b0a0443.png$	$V a \cdot a \cdot a = a^3$ $a$ = the length of one side
Rectangular prism	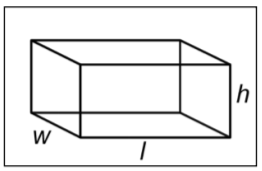$clipboard_e25e09b5b85bcd3a6443b94f681203adb.png$	$V = l \cdot w \cdot h$ $l$ = length $w$ = width $h$ = height
Pyramid	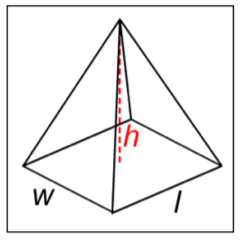$clipboard_e2264021b0bc84201ed5cf06892e143e6.png$	$V = \dfrac{l \cdot w \cdot h}{3}$ $l$ = length $w$ = width $h$ = height

Remember that all cubes are rectangular prisms, so the formula for finding the volume of a cube is the area of the base of the cube times the height.

Now let’s look at solids that have a circular base.

Name

Transparent Form

Volume Formula

Cylinder

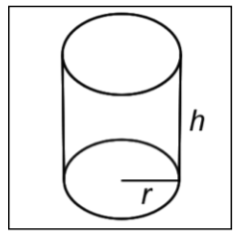$clipboard_e96b5ca11b4a4dd5cc0c267cf2bfdaa70.png$

$V = \pi \cdot r^2 \cdot h$

$r$ = radius

$h$ = height

Cone

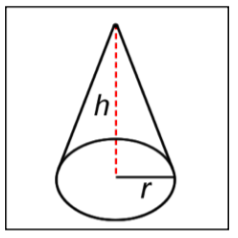$clipboard_ed0cc77e4d6c7cbe9cb87a1a6b1832af3.png$

$V = \dfrac{\pi \cdot r^2 \cdot h}{3}$

$r$ = radius

$h$ = height

Here you see the number $\pi$ again.

The volume of a cylinder is the area of its base, $\pi r^2$, times its height, $h$.

Compare the formula for the volume of a cone ($V = \dfrac{\pi \cdot r^2 \cdot h}{3}$) with the formula for the volume of a pyramid ($V = \dfrac{l \cdot w \cdot h}{3}$). The numerator of the cone formula is the volume formula for a cylinder, and the numerator of the pyramid formula is the volume formula for a rectangular prism. Then divide each by 3 to find the volume of the cone and the pyramid. Looking for patterns and similarities in the formulas can help you remember which formula refers to a given solid.

Finally, the formula for a sphere is provided below. Notice that the radius is cubed, not squared and that the quantity $\pi r^3$ is multiplied by $\dfrac{4}{3}$.

Name

Wireframe Form

Volume Formula

Sphere

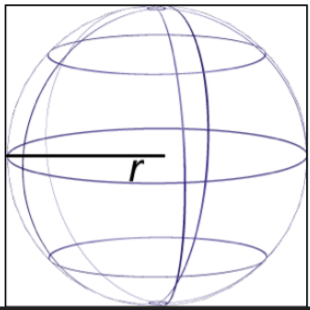$clipboard_e29828a88228afda41785f730489daec8.png$

$V = \dfrac{4}{3} \pi r^3$

$r$ = radius

Applying the Formulas You know how to identify the solids, and you also know the volume formulas for these solids. To calculate the actual volume of a given shape, all you need to do is substitute the solid’s dimensions into the formula and calculate.

In the examples below, notice that cubic units ($\text{meters}^3$, $\text{inches}^3$, $\text{feet }^3$) are used.

Example $\PageIndex{2}$

Find the volume of a cube with side lengths of 6 meters.

Solution

Identify the proper formula to use. $a$ = side length

$V = a \cdot a \cdot a = a^3$

Substitute $a = 6$ into the formula.

$V = 6 \cdot 6 \cdot 6 = 6^3$

Calculate the volume.

$6 \cdot 6 \cdot 6 = 216$

Recall, we use cubic units with volume.

Answer: Volume = $216 \text{ meters}^3$

Example $\PageIndex{3}$

Find the volume of the shape shown below.

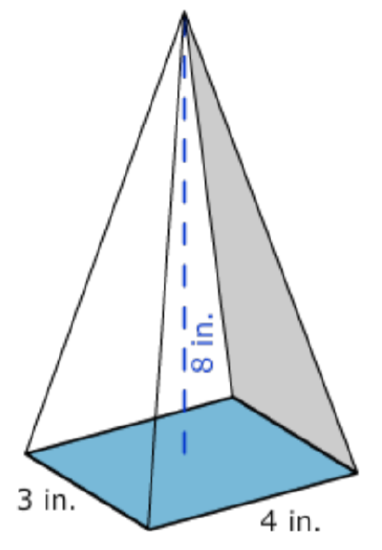
$clipboard_ee404233dc4e707fb1191005e77e385b9.png$

Solution

Identify the shape. It has a rectangular base and rises to a point, so it is a pyramid.

Identify the proper formula to use. $l$ = length, $w$ = width, and $h$ = height

$V = \dfrac{l \cdot w \cdot h}{3}$

Use the image to identify the dimensions. $4$ = length $3$ = width $8$ = height. Then substitute $l$ = 4, $w$ = 3, and $h$ = 8 into the formula.

$V = \dfrac{4 \cdot 3 \cdot 8}{3}$

Calculate the volume.

$V = \dfrac{96}{3}$

$= 32$

Answer: The volume of the pyramid is $32 \text{ inches}^3$

Example $\PageIndex{4}$

Find the volume of the shape shown below. Use $3.14$ for $\pi$, and round the answer to the nearest hundredth.

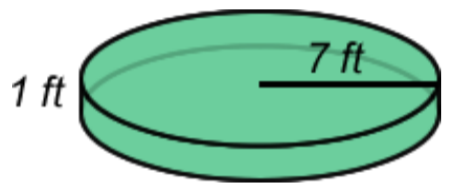
$clipboard_e905a6d40e0b2d9f835ba7e815a0c4ef6.png$

Solution

Identify the shape. It has a circular base and has uniform thickness (or height), so it is a cylinder.

Identify the proper formula to use.

$V = \pi \cdot r^2 \cdot h$

Use the image to identify the dimensions. Then substitute $r = 7$ and $h = 1$ into the formula.

$V = \pi \cdot 7^2 \cdot 1$

Calculate the volume, using $3.14$ as an approximation for $\pi$.

$V = \pi \cdot 7^2 \cdot 1$

$= 49 \pi$

$≈ 153.86$

Answer: The volume is $49 \pi$ or approximately $153.86 \text{ feet}^3$.

Try It Now 1

Find the volume of a rectangular prism that is 8 inches long, 3 inches wide, and 10 inches tall.

Composite Solids

Composite geometric solids are made from two or more geometric solids. You can find the volume of these solids as well, as long as you are able to figure out the individual solids that make up the composite shape.

Look at the image of a capsule below. Each end is a half-sphere. You can find the volume of the solid by taking it apart. What solids can you break this shape into?

$clipboard_ebe96dd1c10187389fc3d1d6a3f88b828.png$

You can break it into a cylinder and two half-spheres.

$clipboard_ef8ad539fb32500b4eaa9befd635866f1.png$

Two half-spheres form a whole one, so if you know the volume formulas for a cylinder and a sphere, you can find the volume of this capsule.

Example $\PageIndex{5}$

If the radius of the spherical ends is 6 inches, find the volume of the solid below. Use $3.14$ for $\pi$. Round your final answer to the nearest whole number.

$clipboard_e86779794caaa4e3e09cd4ddbaa6ebdd4.png$

Solution

Identify the composite solids. This capsule can be thought of as a cylinder with a half-sphere on each end.

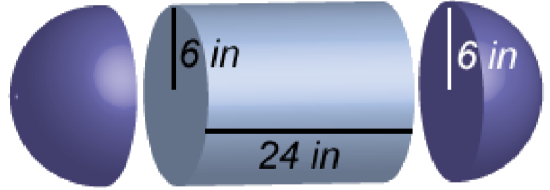
$clipboard_e2c1e3a48485ab5877ca5d46e494b1322.png$

Identify the proper formulas to use.

$\text{Volume of a cylinder: } \pi \cdot r^2 \cdot h$

$\text{Volume of a sphere: } \dfrac{4}{3} \pi r^3$

Substitute the dimensions into the formulas.

$\text{Volume of a cylinder: } \pi \cdot 6^2 \cdot 24$

$\text{Volume of a sphere: } \dfrac{4}{3} \pi \cdot 6^3$

The height of a cylinder refers to the section between the two circular bases. This dimension is given as 24 inches, so $h$ = 24. The radius of the sphere is 6 inches. You can use $r$ = 6 in both formulas.

$\text{Volume of a cylinder: } \pi \cdot 36 \cdot 24$

$= 864 \cdot \pi$

$≈ 2712.96$

Calculate the volume of the cylinder and the sphere.

$\text{Volume of a sphere: } \dfrac{4}{3} \pi \cdot 216$

$= 288 \cdot \pi$

$≈ 904.32$

Add the volumes.

$\text{Volume of capsule: } 2712.96 + 904.32 ≈ 3617.28 $

Answer: The volume of the capsule is $1152 \pi$ or approximately $3617 \text{ inches}^3$.

Example $\PageIndex{6}$

A sculptor carves a rectangular prism out of a solid piece of wood. Then, at the top, she hollows out an inverted pyramid. The solid, and its dimensions, are shown at right. What is the volume of the finished piece?

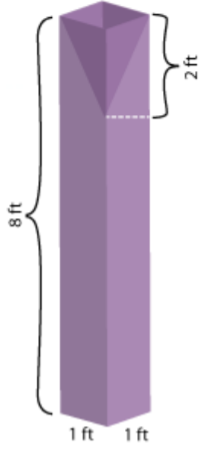
$clipboard_ebc25bb8b2530c3626ef3913029ea11dc.png$

Solution

Identify the composite solids. This sculpture can be thought of as a rectangular prism with a pyramid removed.

Identify the proper formulas to use.

$\text{Volume of rectangular prism: } l \cdot w \cdot h$

$\text{Volume of pyramid: } \dfrac{l \cdot w \cdot h}{3}$

Substitute the dimensions into the formulas, and calculate.

$\text{Volume of rectangular prism: } 1 \cdot 1 \cdot 8 = 8$

$\text{Volume of pyramid: } \dfrac{1 \cdot 1 \cdot 2}{3} = \dfrac{2}{3}$

Subtract the volume of the pyramid from the volume of the rectangular prism.

$\text{Volume of sculpture: } V = 8 - \dfrac{2}{3} $

$= 7\dfrac{1}{3}$

Answer: The volume of the sculpture is $7\dfrac{1}{3} \text{ feet}^3$.

Try It Now 2

A machine takes a solid cylinder with a height of 9 mm and a diameter of 7 mm and bores a hole all the way through it. The hole that it creates has a diameter of 3 mm. Which of the following expressions would correctly find the volume of the solid?

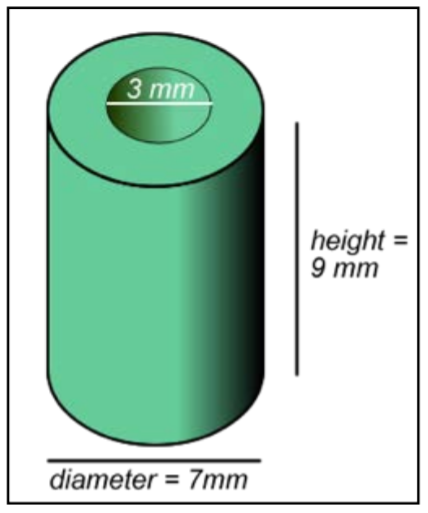
$clipboard_ec3658031a6bf6ee8eaa813433d02c5ac.png$

A) $(\pi \cdot 7^2 \cdot 9) - (\pi \cdot 3^2 \cdot 9) $

B) $(\pi \cdot 3.5^2 \cdot 9) - (\pi \cdot 1.5^2 \cdot 9) $

C) $(\pi \cdot 7^2 \cdot 9) + (\pi \cdot 3^2 \cdot 9) $

D) $(\pi \cdot 3.5^2 \cdot 9) + (\pi \cdot 1.5^2 \cdot 9) $

Summary

Three-dimensional solids have length, width, and height. You use a measurement called volume to figure out the amount of space that these solids take up. To find the volume of a specific geometric solid, you can use a volume formula that is specific to that solid. Sometimes, you will encounter composite geometric solids. These are solids that combine two or more basic solids. To find the volume of these, identify the simpler solids that make up the composite figure, find the volumes of those solids, and combine them as needed.

Note

1. $240 \text{ inches}^3 $; to find the volume of the rectangular prism, use the formula $V = l \cdot w \cdot h$, and then substitute in the values for the length, width, and height. $8 \text{ inches} \cdot 3 \text{ inches} \cdot 10 \text{ inches} = 240 \text{ inches}^3$.

2. B) $(\pi \cdot 3.5^2 \cdot 9) - (\pi \cdot 1.5^2 \cdot 9) $; you find the volume of the entire cylinder by multiplying $\pi \cdot 3.5^2 \cdot 9$, then subtract the empty cylinder in the middle, which is found by multiplying $\pi \cdot 1.5^2 \cdot 9$.

Glossary

acute triangle	An angle measuring less than 90º.
angle	A figure formed by the joining of two rays with a common endpoint.
area	The amount of space inside a two-dimensional shape, measured in square units.
circumference	The distance around a circle, calculated by the formula $C = \pi d$.
complementary angles	Two angles whose measurements add up to 90º.
cone	A solid figure with a single circular base and a round, smooth face that diminishes to a single point.
congruent	Having the same size and shape.
corresponding angles	Angles of separate figures that are in the same position within each figure.
corresponding sides	Sides of separate figures that are opposite corresponding angles.
cube	A six-sided polyhedron that has congruent squares as faces.
cylinder	A solid figure with a pair of circular, parallel bases and a round, smooth face between them.
diameter	The length across a circle, passing through the center of the circle. A diameter is equal to the length of two radii.
equilateral triangle	A triangle with 3 equal sides. Equilateral triangles also have three angles that measure the same.
face	The flat surface of a solid figure.
hypotenuse	The side opposite the right angle in any right triangle. The hypotenuse is the longest side of any right triangle.
isosceles trapezoid	A trapezoid with one pair of parallel sides and another pair of opposite sides that are congruent.
isosceles triangle	A triangle with 2 equal sides and 2 equal angles.
leg, legs	In a right triangle, one of the two sides creating a right angle.
line	A line is a one-dimensional figure, which extends without end in two directions.
line segment	A finite section of a line between any two points that lie on the line.
obtuse angle, obtuse angles	An angle measuring more than 90º and less than 180º.
obtuse triangle	A triangle with one angle that measures between 90º and 180º.
parallel lines	Two or more lines that lie in the same plane but which never intersect.
parallelogram, parallelograms	A quadrilateral with two pairs of parallel sides.
perimeter	The distance around a two-dimensional shape.
perpendicular lines	Two lines that lie in the same plane and intersect at a 90º angle.
pi	The ratio of a circle’s circumference to its diameter. Pi is denoted by the Greek letter $\pi$. It is often approximated as $3.14$ or $\dfrac{22}{7}$.
plane	In geometry, a two-dimensional surface that continues infinitely. Any three individual points that don't lie on the same line will lie on exactly one plane.
point	A zero-dimensional object that defines a specific location on a plane. It is represented by a small dot.
polygon, polygons	A closed plane figure with three or more straight sides.
polyhedron, polyhedrons	A solid whose faces are polygons.
pyramid, pyramids	A polyhedron with a polygonal base and a collection of triangular faces that meet at a point.
Pythagorean Theorem	The formula that relates the lengths of the sides of any right triangle: $a^2 + b^2 + c^2$, where $c$ is the hypotenuse, and $a$ and $b$ are the legs of the right triangle.
quadrilateral, quadrilaterals	A four-sided polygon.
radius	The distance from the center of a circle to any point on the circle.
ray	A half-line that begins at one point and goes on forever in one direction.
rectangle	A quadrilateral with two pairs of parallel sides and four right angles.
rectangular prism	A polyhedron that has three pairs of congruent, rectangular, parallel faces.
rhombus	A quadrilateral with four congruent sides.
right angle	An angle measuring exactly 90º.
right triangle, right triangles	A triangle containing a right angle.
scalene triangle	A triangle in which all three sides are a different length.
similar	Having the same shape but not necessarily the same size.
sphere	A solid, round figure where every point on the surface is the same distance from the center.
square	A quadrilateral whose sides are all congruent and which has four right angles.
straight angle	An angle measuring exactly 180º.
supplementary angles	Two angles whose measurements add up to 180º.
trapezoid	A quadrilateral with one pair of parallel sides.
triangle	A polygon with three sides.
vertex	A turning point in a graph. Also the endpoint of the two rays that form an angle.
volume	A measurement of how much it takes to fill up a three-dimensional figure. Volume is measured in cubic units.

Search

Learning Objectives

Introduction

Identifying Solids

Example \(\PageIndex{1}\)

Solution

Volume

Example \(\PageIndex{2}\)

Solution

Example \(\PageIndex{3}\)

Solution

Example \(\PageIndex{4}\)

Solution

Try It Now 1

Composite Solids

Example \(\PageIndex{5}\)

Solution

Example \(\PageIndex{6}\)

Solution

Try It Now 2

Summary

Note

Glossary