2.2: Perimeter, Circumference, and Area
- Last updated
- Save as PDF
- Page ID
- 109870
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)6.2.1: Quadrilaterals
Learning Objective
- Identify properties, including angle measurements, of quadrilaterals.
Introduction
Quadrilaterals are a special type of polygon. As with triangles and other polygons, quadrilaterals have special properties and can be classified by characteristics of their angles and sides. Understanding the properties of different quadrilaterals can help you in solving problems that involve this type of polygon.
Defining a Quadrilateral
Picking apart the name “quadrilateral” helps you understand what it refers to. The prefix “quad-” means “four,” and “lateral” is derived from the Latin word for “side.” So a quadrilateral is a foursided polygon.
Since it is a polygon, you know that it is a two-dimensional figure made up of straight sides. A quadrilateral also has four angles formed by its four sides. Below are some examples of quadrilaterals. Notice that each figure has four straight sides and four angles.
Interior Angles of a Quadrilateral
The sum of the interior angles of any quadrilateral is 360°. Consider the two examples below.
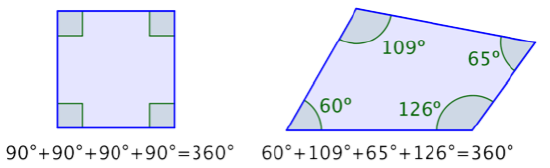
You could draw many quadrilaterals such as these and carefully measure the four angles. You would find that for every quadrilateral, the sum of the interior angles will always be 360°.
You can also use your knowledge of triangles as a way to understand why the sum of the interior angles of any quadrilateral is 360°. Any quadrilateral can be divided into two triangles as shown in the images below.
In the first image, the quadrilaterals have each been divided into two triangles. The angle measurements of one triangle are shown for each.
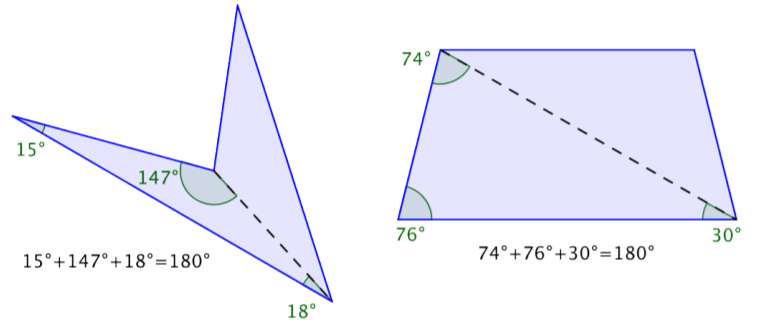
These measurements add up to 180º. Now look at the measurements for the other triangles—they also add up to 180º!
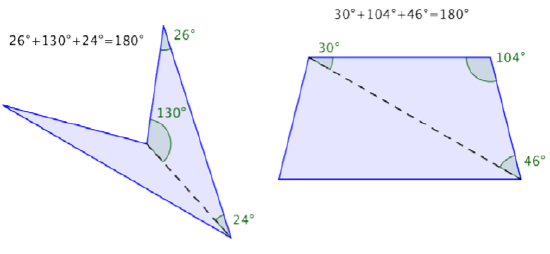
Since the sum of the interior angles of any triangle is 180° and there are two triangles in a quadrilateral, the sum of the angles for each quadrilateral is 360°.
Specific Types of Quadrilaterals
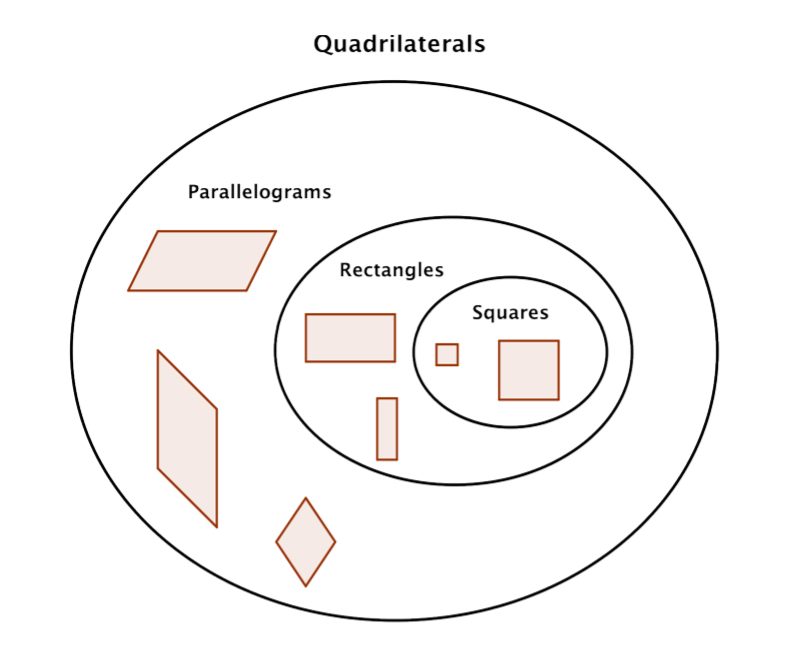
Let’s start by examining the group of quadrilaterals that have two pairs of parallel sides. These quadrilaterals are called parallelograms. They take a variety of shapes, but one classic example is shown below.
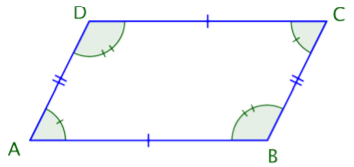
Imagine extending the pairs of opposite sides. They would never intersect because they are parallel. Notice, also, that the opposite angles of a parallelogram are congruent, as are the opposite sides. (Remember that “congruent” means “the same size.”) The geometric symbol for congruent is \(≅\), so you can write ∠A ≅ ∠C and ∠B ≅ ∠D. The parallel sides are also the same length: \(\overline{AB} ≅ \overline{DC}\) and \(\overline{BC} ≅ \overline{AD}\). These relationships are true for all parallelograms.
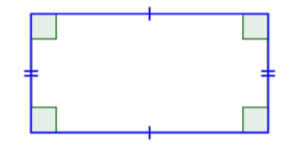
There are two special cases of parallelograms that will be familiar to you from your earliest experiences with geometric shapes. The first special case is called a rectangle. By definition, a rectangle is a parallelogram because its pairs of opposite sides are parallel. A rectangle also has the special characteristic that all of its angles are right angles; all four of its angles are congruent.
The other special case of a parallelogram is a special type of rectangle, a square. A square is one of the most basic geometric shapes. It is a special case of a parallelogram that has four congruent sides and four right angles.
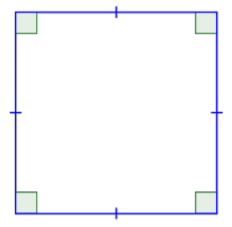
A square is also a rectangle because it has two sets of parallel sides and four right angles. A square is also a parallelogram because its opposite sides are parallel. So, a square can be classified in any of these three ways, with “parallelogram” being the least specific description and “square,” the most descriptive.
Another quadrilateral that you might see is called a rhombus. All four sides of a rhombus are congruent. Its properties include that each pair of opposite sides is parallel, also making it a parallelogram.
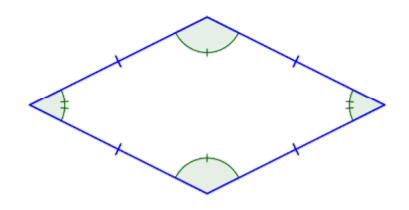
In summary, all squares are rectangles, but not all rectangles are squares. All rectangles are parallelograms, but not all parallelograms are rectangles. And all of these shapes are quadrilaterals.
The diagram below illustrates the relationship between the different types of quadrilaterals.
You can use the properties of parallelograms to solve problems. Consider the example that follows.
Example \(\PageIndex{1}\)
Determine the measures of ∠M and ∠L.
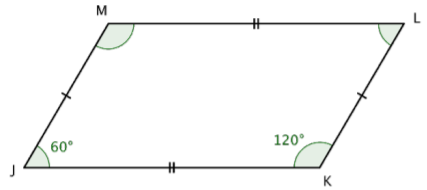
Solution
Identify opposite angles.
∠L is opposite ∠J
∠M is opposite ∠K
A property of parallelograms is that opposite angles are congruent.
∠L ≅ ∠J
∠M ≅ ∠K
Use the given angle measurements to determine measures of opposite angles.
m∠J = 60°, so m∠L = 60°
m∠K = 120°, so m∠M = 120°
Answer: m∠L = 60° and m∠M = 120°
Trapezoids
There is another special type of quadrilateral. This quadrilateral has the property of having only one pair of opposite sides that are parallel. Here is one example of a trapezoid.
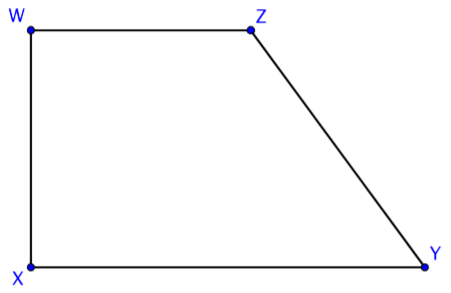
Notice that \(\overline{XY} || \overline{WZ}\), and that \(\overline{WX}\) and \(\overline{ZY}\) are not parallel. You can easily imagine that if you extended sides \(\overline{WX}\) and \(\overline{ZY}\), they would intersect above the figure.
If the non-parallel sides of a trapezoid are congruent, the trapezoid is called an isosceles trapezoid. Like the similarly named triangle that has two sides of equal length, the isosceles trapezoid has a pair of opposite sides of equal length. The other pair of opposite sides is parallel. Below is an example of an isosceles trapezoid.
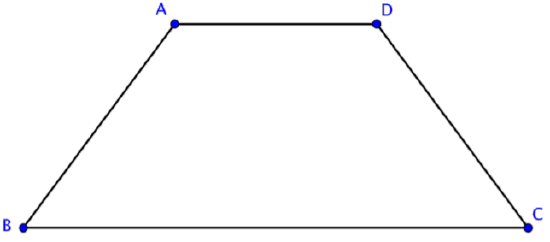
In this trapezoid ABCD, \(\overline{BC} || \overline{AD}\) and \(\overline{AB} ≅ \overline{CD}\).
Try It Now 1
Which of the following statements is true?
A) Some trapezoids are parallelograms.
B) All trapezoids are quadrilaterals.
C) All rectangles are squares.
D) A shape cannot be a parallelogram and a quadrilateral.
You can use the properties of quadrilaterals to solve problems involving trapezoids. Consider the example below.
Example \(\PageIndex{2}\)
Find the measure of ∠Q.
Solution
The sum of the measures of the interior angles of a quadrilateral is 360°.
m∠P + m∠Q + m∠R + m∠S = 360°
The square symbol indicates a right angle.
m∠R = 90°
m∠S = 90°
Since three of the four angle measures are given, you can find the fourth angle measurement.
60° + m∠Q + 90° + 90° = 360°
Calculate the measurement of ∠Q.
m∠Q + 240° = 360°
m∠Q = 120°
From the image, you can see that it is an obtuse angle, so its measure must be greater than 90°.
Answer: m∠Q = 120°
The table below summarizes the special types of quadrilaterals and some of their properties.
| Name of Quadrilateral | Quadrilateral | Description |
| Parallelogram | 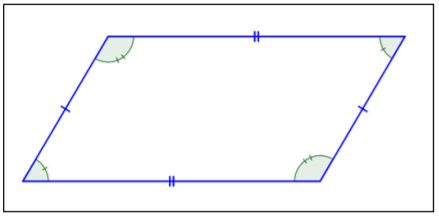 |
2 pairs of parallel sides. Opposite sides and opposite angles are congruent. |
| Rectangle | 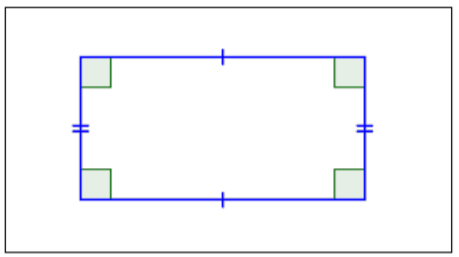 |
2 pairs of parallel sides. 4 right angles (90°). Opposite sides are parallel and congruent. All angles are congruent. |
| Square | 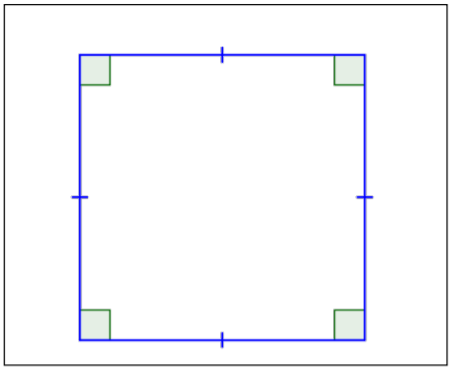 |
4 congruent sides. 4 right angles (90°). Opposite sides are parallel. All angles are congruent. |
| Trapezoid | 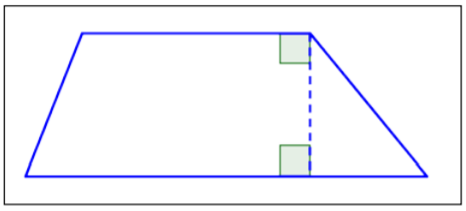 |
Only one pair of opposite sides is parallel. |
Summary
A quadrilateral is a mathematical name for a four-sided polygon. Parallelograms, squares, rectangles, and trapezoids are all examples of quadrilaterals. These quadrilaterals earn their distinction based on their properties, including the number of pairs of parallel sides they have and their angle and side measurements.
Try It Now Answers
1. B) All trapezoids are quadrilaterals; trapezoids are four-sided polygons, so they are all quadrilaterals.
6.2.2: Perimeter and Area
Learning Objectives
- Find the perimeter of a polygon.
- Find the area of a polygon.
- Find the area and perimeter of non-standard polygons
Introduction
Perimeter and area are two important and fundamental mathematical topics. They help you to quantify physical space and also provide a foundation for more advanced mathematics found in algebra, trigonometry, and calculus. Perimeter is a measurement of the distance around a shape and area gives us an idea of how much surface the shape covers.
Knowledge of area and perimeter is applied practically by people on a daily basis, such as architects, engineers, and graphic designers, and is math that is very much needed by people in general. Understanding how much space you have and learning how to fit shapes together exactly will help you when you paint a room, buy a home, remodel a kitchen, or build a deck.
Perimeter
The perimeter of a two-dimensional shape is the distance around the shape. You can think of wrapping a string around a triangle. The length of this string would be the perimeter of the triangle. Or walking around the outside of a park, you walk the distance of the park’s perimeter. Some people find it useful to think “peRIMeter” because the edge of an object is its rim and peRIMeter has the word “rim” in it.
If the shape is a polygon, then you can add up all the lengths of the sides to find the perimeter. Be careful to make sure that all the lengths are measured in the same units. You measure perimeter in linear units, which is one-dimensional. Examples of units of measure for length are inches, centimeters, or feet.
Example \(\PageIndex{3}\)
Find the perimeter of the given figure. All measurements indicated are inches.
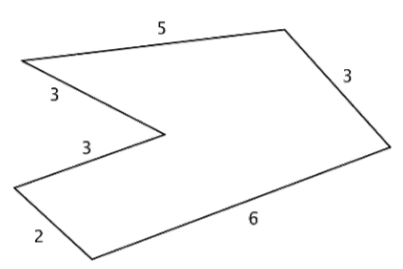
Solution
Since all the sides are measured in inches, just add the lengths of all six sides to get the perimeter.
\(P = 5 + 3 + 6 + 2 + 3 + 3\)
Remember to include units.
Answer: \(P = 22 \text{ inches}\)
This means that a tightly wrapped string running the entire distance around the polygon would measure 22 inches long.
Example \(\PageIndex{4}\)
Find the perimeter of a triangle with sides measuring 6 cm, 8 cm, and 12 cm.
Solution
Since all the sides are measured in centimeters, just add the lengths of all three sides to get the perimeter.
\(P = 6 + 8 + 12\)
Answer: \(P = 26 \text{ centimeters}\)
Sometimes, you need to use what you know about a polygon in order to find the perimeter. Let’s look at the rectangle in the next example.
Example \(\PageIndex{5}\)
A rectangle has a length of 8 centimeters and a width of 3 centimeters. Find the perimeter.
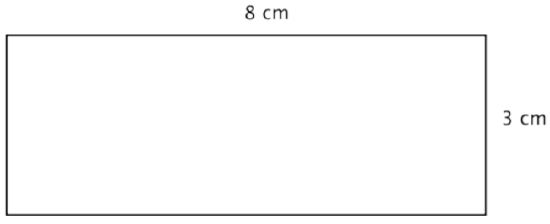
Solution
Since this is a rectangle, the opposite sides have the same lengths, 3 cm. and 8 cm. Add up the lengths of all four sides to find the perimeter.
\(P = 3 + 3 + 8 + 8\)
Answer \(P = 22 \text{ cm}\)
Notice that the perimeter of a rectangle always has two pairs of equal-length sides. In the above example, you could have also written \(P = 2(3) + 2(8) = 6 + 16 = 22 \text{ cm}\). The formula for the perimeter of a rectangle is often written as \(P = 2l + 2w\), where \(l\) is the length of the rectangle and \(w\) is the width of the rectangle.
Area of Parallelograms
The area of a two-dimensional figure describes the amount of surface the shape covers. You measure area in square units of a fixed size. Examples of square units of measure are square inches, square centimeters, or square miles. When finding the area of a polygon, you count how many squares of a certain size will cover the region inside the polygon.
Let’s look at a 4 x 4 square.
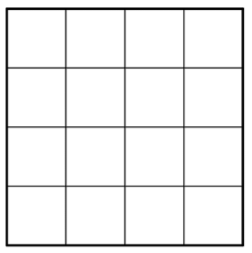
You can count that there are 16 squares, so the area is 16 square units. Counting out 16 squares doesn’t take too long, but what about finding the area if this is a larger square or the units are smaller? It could take a long time to count.
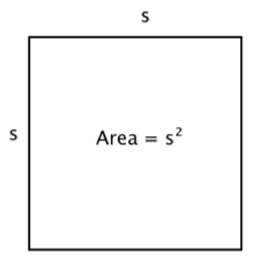
Fortunately, you can use multiplication. Since there are 4 rows of 4 squares, you can multiply \(4 \cdot 4\) to get \(16\) squares! And this can be generalized to a formula for finding the area of a square with any length, \(s\): \(\text{Area } = s \cdot s = s^2\).
You can write “\(\text{in}^2\)” for square inches and “\(\text{ft}^2\)” for square feet.
To help you find the area of the many different categories of polygons, mathematicians have developed formulas. These formulas help you find the measurement more quickly than by simply counting. The formulas you are going to look at are all developed from the understanding that you are counting the number of square units inside the polygon. Let’s look at a rectangle.
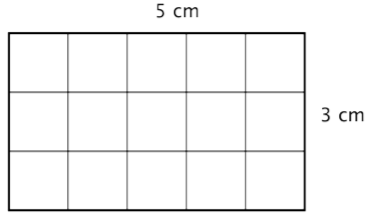
You can count the squares individually, but it is much easier to multiply 3 times 5 to find the number more quickly. And, more generally, the area of any rectangle can be found by multiplying length times width.
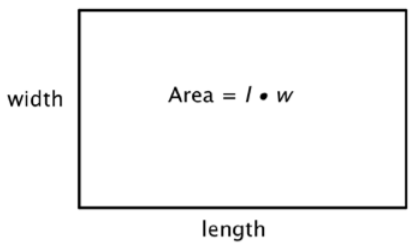
Example \(\PageIndex{6}\)
A rectangle has a length of 8 centimeters and a width of 3 centimeters. Find the area.
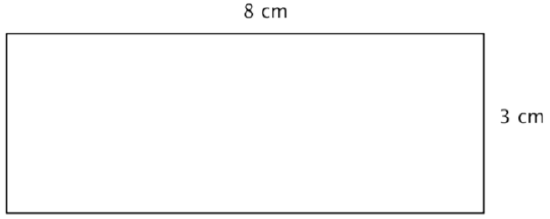
Solution
Start with the formula for the area of a rectangle, which multiplies the length times the width.
\(A = l \cdot w\)
Substitute 8 for the length and 3 for the width.
\(A = 8 \cdot 3\)
Be sure to include the units, in this case, square cm.
Answer: \(A = 24 \text{ cm}^2\)
It would take 24 squares, each measuring 1 cm on a side, to cover this rectangle.
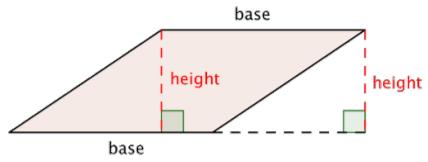
The formula for the area of any parallelogram (remember, a rectangle is a type of parallelogram) is the same as that of a rectangle: \(\text{Area } = l \cdot w\). Notice in a rectangle, the length and the width are perpendicular. This should also be true for all parallelograms. Base (b) for the length (of the base), and height (h) for the width of the line perpendicular to the base is often used. So, the formula for a parallelogram is generally written, \(\text{Area } = b \cdot h\).
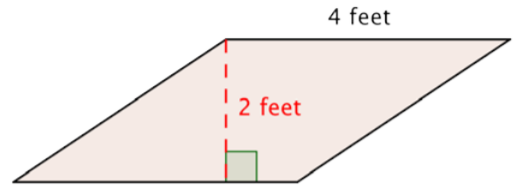
Example \(\PageIndex{7}\)
Find the area of the parallelogram.
Solution
Start with the formula for the area of a parallelogram: \(\text{Area } = \text{base} \cdot \text{height}\).
\(A = b \cdot h\)
Substitute the values into the formula.
\(A = 4 \cdot 2\)
Multiply.
\(A = 8\)
Answer: The area of the parallelogram is \(8 \text{ ft}^2\).
Try It Now 1
Find the area of a parallelogram with a height of 12 feet and a base of 9 feet.
Area of Triangles and Trapezoids
The formula for the area of a triangle can be explained by looking at a right triangle. Look at the image below—a rectangle with the same height and base as the original triangle. The area of the triangle is one half of the rectangle!
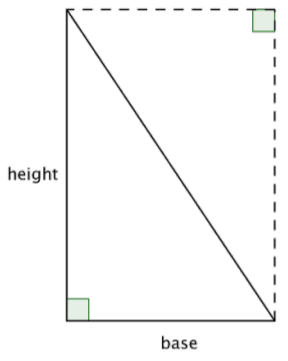
Since the area of two congruent triangles is the same as the area of a rectangle, you can come up with the formula \(\text{Area } = \dfrac{1}{2}bh\) to find the area of a triangle.
When you use the formula for a triangle to find its area, it is important to identify a base and its corresponding height, which is perpendicular to the base.
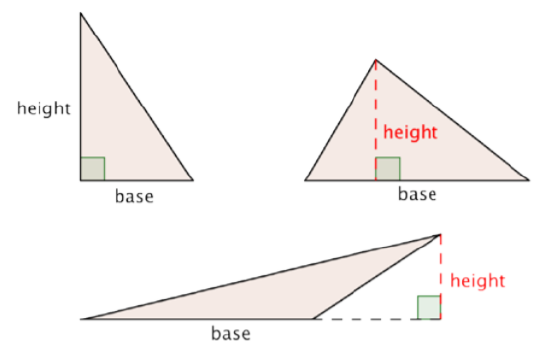
Example \(\PageIndex{8}\)
A triangle has a height of 4 inches and a base of 10 inches. Find the area.
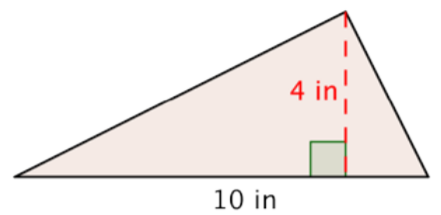
Solution
Start with the formula for the area of a triangle.
\(A = \dfrac{1}{2}bh\)
Substitute 10 for the base and 4 for the height.
\(A = \dfrac{1}{2} \cdot (10) \cdot (4)\)
Multiply.
\(A = \dfrac{1}{2} \cdot 40\)
\(A = 20\)
Answer: \(A = 20 \text{ in}^2\)
Now let’s look at the trapezoid. To find the area of a trapezoid, take the average length of the two parallel bases and multiply that length by the height: \(A = \dfrac{(b_1 + b_2)}{2}h\).
An example is provided below. Notice that the height of a trapezoid will always be perpendicular to the bases (just like when you find the height of a parallelogram).
Example \(\PageIndex{9}\)
Find the area of the trapezoid.
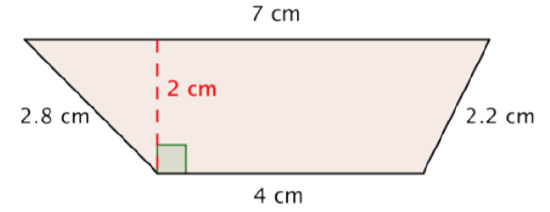
Solution
Start with the formula for the area of a trapezoid.
\(A = \dfrac{(b_1 + b_2)}{2}h\)
Substitute 4 and 7 for the bases and 2 for the height, and find A.
\(A = \dfrac{(4 + 7)}{2} \cdot 2\)
\(A = \dfrac{11}{2} \cdot 2\)
\(A = 11\)
Answer: The area of the trapezoid is \(11 \text{ cm}^2\)
Area Formulas
Use the following formulas to find the areas of different shapes.
square: \(A = s^2\)
rectangle: \(A = l \cdot w\)
parallelogram: \(A = b \cdot h\)
triangle: \(A = \dfrac{1}{2}b \cdot h\)
trapezoid: \(A = \dfrac{(b_1 + b_2)}{2}h\)
Working with Perimeter and Area
Often you need to find the area or perimeter of a shape that is not a standard polygon. Artists and architects, for example, usually deal with complex shapes. However, even complex shapes can be thought of as being composed of smaller, less complicated shapes, like rectangles, trapezoids, and triangles.
To find the perimeter of non-standard shapes, you still find the distance around the shape by adding together the length of each side.
Finding the area of non-standard shapes is a bit different. You need to create regions within the shape for which you can find the area and add these areas together. Have a look at how this is done below.
Example \(\PageIndex{10}\)
Find the area and perimeter of the polygon.
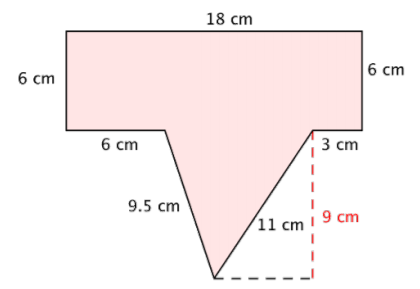
Solution
To find the perimeter, add together the lengths of the sides. Start at the top and work clockwise around the shape.
\(P = 18 + 6 + 3 + 11 + 9.5 + 6 + 6\)
\(P = 59.5 \text{ cm}\)
To find the area, divide the polygon into two separate, simpler regions. The area of the entire polygon will equal the sum of the areas of the two regions.
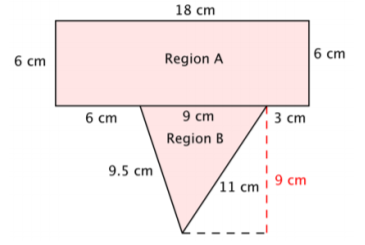
\(\text{Area of Polygon } = (\text{Area of A}) + (\text{Area of B})\)
Region A is a rectangle. To find the area, multiply the length (18) by the width (6).
\(\text{Area of Region }A = l \cdot w\)
\(= 18 \cdot 6\)
\(= 108\)
The area of Region A is \(108 \text{ cm}^2\).
Region B is a triangle. To find the area, use the formula \(\dfrac{1}{2}bh\), where the base is 9 and the height is 9.
\(\text{Area of Region }B = \dfrac{1}{2}b \cdot h\)
\(= \dfrac{1}{2} \cdot 9 \cdot 9\)
\(= \dfrac{1}{2} \cdot 81\)
\(= 40.5\)
The area of Region B is \(40.5 \text{ cm}^2\).
Add the regions together.
\(108 \text{ cm}^2\) + \(40.5 \text{ cm}^2\) = \(148.5 \text{ cm}^2\).
Answer: Perimeter = \(59.5 \text{ cm}\)
Area = \(148.5 \text{ cm}^2\)
You also can use what you know about perimeter and area to help solve problems about situations like buying fencing or paint, or determining how big a rug is needed in the living room. Here’s a fencing example.
Example \(\PageIndex{11}\)
Rosie is planting a garden with the dimensions shown below. She wants to put a thin, even layer of mulch over the entire surface of the garden. The mulch costs $3 a square foot. How much money will she have to spend on mulch?
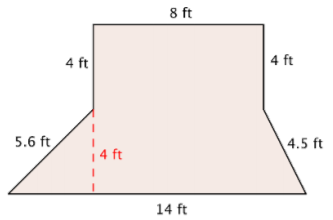
Solution
This shape is a combination of two simpler shapes: a rectangle and a trapezoid. Find the area of each.
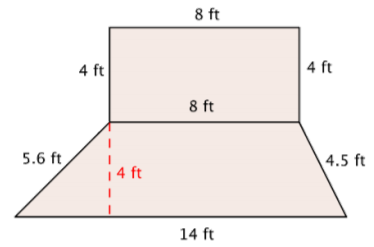
Find the area of the rectangle.
\(A = l \cdot w\)
\(A = 8 \cdot 4\)
\(A = 32 \text{ ft}^2\)
Find the area of the trapezoid.
\(A = \dfrac{(b_1 + b_2)}{2}h\)
\(A = \dfrac{(14 + 8)}{2} \cdot 4\)
\(A = \dfrac{22}{2} \cdot 4\)
\(A = 11 \cdot 4\)
\(A = 44 \text{ ft}^2\)
Add the measurements.
\(32 \text{ ft}^2 + 44 \text{ ft}^2 = 76 \text{ ft}^2\)
Multiply by $3 to find out how much Rosie will have to spend.
\(76 \text{ ft}^2 \cdot $3 = $228\)
Answer: Rosie will spend $228 to cover her garden with mulch.
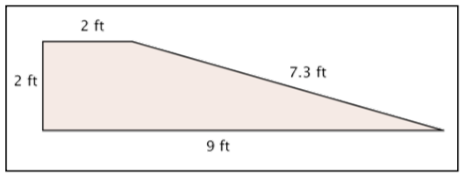
Try It Now 2
Find the area of the given shape.
Summary
The perimeter of a two-dimensional shape is the distance around the shape. It is found by adding up all the sides (as long as they are all the same unit). The area of a two-dimensional shape is found by counting the number of squares that cover the shape. Many formulas have been developed to quickly find the area of standard polygons, like triangles and parallelograms.
Try It Now Answers
1. \(108 \text{ ft}^2\); the height of the parallelogram is \(12\) and the base of the parallelogram is \(9\); the area is \(12\) times \(9\), or \(108 \text{ ft}^2\).
2. \(11 \text{ ft}^2\) ; this shape is a trapezoid, so you can use the formula \(A = \dfrac{(b_1 + b_2)}{2}h\) to find the area: \(A = \dfrac{(2 + 9)}{2}\cdot 2\).
6.2.3: Circles
Learning Objectives
- Identify properties of circles.
- Find the circumference of a circle.
- Find the area of a circle.
- Find the area and perimeter of composite geometric figures.
Introduction
Circles are a common shape. You see them all over—wheels on a car, Frisbees passing through the air, compact discs delivering data. These are all circles.
A circle is a two-dimensional figure just like polygons and quadrilaterals. However, circles are measured differently than these other shapes—you even have to use some different terms to describe them. Let’s take a look at this interesting shape.
Properties of Circles
A circle represents a set of points, all of which are the same distance away from a fixed, middle point. This fixed point is called the center. The distance from the center of the circle to any point on the circle is called the radius.
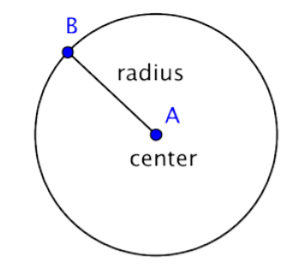
When two radii (the plural of radius) are put together to form a line segment across the circle, you have a diameter. The diameter of a circle passes through the center of the circle and has its endpoints on the circle itself.
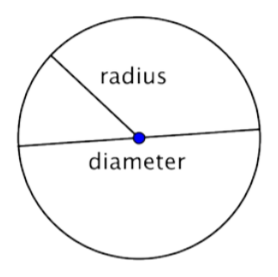
The diameter of any circle is two times the length of that circle’s radius. It can be represented by the expression 2r, or “two times the radius.” So, if you know a circle’s radius, you can multiply it by 2 to find the diameter; this also means that if you know a circle’s diameter, you can divide by 2 to find the radius.
Example \(\PageIndex{12}\)
Find the diameter of the circle.
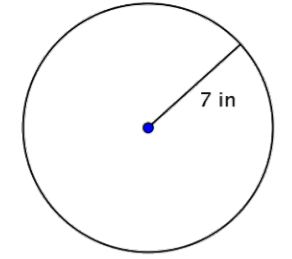
Solution
The diameter is two times the radius, or 2r. The radius of this circle is 7 inches, so the diameter is 2(7) = 14 inches.
\(d = 2r\)
\(d = 2(7)\)
\(d = 14\)
Answer: The diameter is 14 inches.
Example \(\PageIndex{13}\)
Find the radius of the circle.
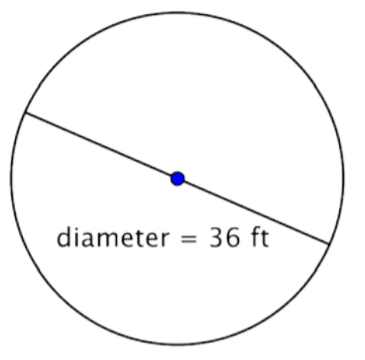
Solution
The radius is half the diameter, or \(\dfrac{1}{2}d\).
\(r = \dfrac{1}{2}d\)
\(r = \dfrac{1}{2}(36)\)
\(r = 18\)
The diameter of this circle is \(36 \text{ feet}\), so the radius is \(r = \dfrac{1}{2}(36) = 18 \text{ feet}\).
Answer: The radius is 18 feet.
Circumference
The distance around a circle is called the circumference. (Recall, the distance around a polygon is the perimeter.)
One interesting property about circles is that the ratio of a circle’s circumference and its diameter is the same for all circles. No matter the size of the circle, the ratio of the circumference and diameter will be the same.
Some actual measurements of different items are provided below. The measurements are accurate to the nearest millimeter or quarter-inch (depending on the unit of measurement used). Look at the ratio of the circumference to the diameter for each one—although the items are different, the ratio for each is approximately the same.
| Item | Circumference (\(C\)) (rounded to nearest hundredth) | Diameter (\(d\)) | Ratio \(\dfrac{C}{d}\) |
| Cup | 253 mm | 79 mm | \(\dfrac{253}{79} = 3.2025...\) |
| Quarter | 84 mm | 27 mm | \(\dfrac{84}{27} = 3.1111...\) |
| Bowl | 37.25 in | 11.5 in | \(\dfrac{37.25}{11.75} = 3.1702...\) |
The circumference and the diameter are approximate measurements since there is no precise way to measure these dimensions exactly. If you were able to measure them more precisely, however, you would find that the ratio \(\dfrac{C}{d}\) would move towards \(3.14\) for each of the items given. The mathematical name for the ratio \(\dfrac{C}{d}\) is pi and is represented by the Greek letter \(\pi\).
\(\pi\) is a non-terminating, non-repeating decimal, so it is impossible to write it out completely? The first 10 digits of \(\pi\) are 3.141592653; it is often rounded to 3.14 or estimated as the fraction \(\dfrac{22}{7}\). Note that both 3.14 and \(\dfrac{22}{7}\) are approximations of \(\pi\), and are used in calculations where it is not important to be precise.
Since you know that the ratio of circumference to diameter (or \(\pi\)) is consistent for all circles, you can use this number to find the circumference of a circle if you know its diameter.
\(\dfrac{C}{d} = \pi, \text{ so } C = \pi d\)
Also, since \(d = 2r\), then \(C = \pi d = \pi (2r) = 2 \pi r\).
Circumference of a Circle
To find the circumference (\(C\)) of a circle, use one of the following formulas:
If you know the diameter (\(d\)) of a circle: \(C = \pi d\))
If you know the radius (\(r\)) of a circle: \(C = 2 \pi r\))
Example \(\PageIndex{14}\)
Find the circumference of the circle.
Solution
To calculate the circumference given a diameter of 9 inches, use the formula \(C = \pi d\). Use 3.14 as an approximation for \(\pi\). Since you are using an approximation for \(\pi\), you cannot give an exact measurement of the circumference. Instead, you use the symbol \(≈\) to indicate “approximately equal to.”
\(C = \pi d\)
\(C = \pi \cdot 9\)
\(C ≈ 3.14 \cdot 9\)
\(C ≈ 28.26\)
Answer: The circumference is \(9\pi\) or approximately \(28.26 \text{ inches}\).
Example \(\PageIndex{15}\)
Find the circumference of a circle with a radius of 2.5 yards.
Solution
To calculate the circumference of a circle given a radius of 2.5 yards, use the formula \(C = 2 \pi r\). Use 3.14 as an approximation for \(\pi\).
\(C = 2 \pi r\)
\(C = 2 \pi \cdot 2.5\)
\(C = \pi \cdot 5\)
\(C ≈ 3.14 \cdot 5\)
\(C ≈ 15.7\)
Answer: The circumference is \(5\pi\) or approximately \(15.7 \text{ yards}\).
Try It Now 1
A circle has a radius of 8 inches. What is its circumference, rounded to the nearest inch?
Area
Pi, \(\pi\), is an important number in geometry. You have already used it to calculate the circumference of a circle. You use \(\pi\) when you are figuring out the area of a circle, too.
Area of a Circle
To find the area (\(A\)) of a circle, use the formula: \(A = \pi r^2\)
Example \(\PageIndex{16}\)
Find the area of the circle.
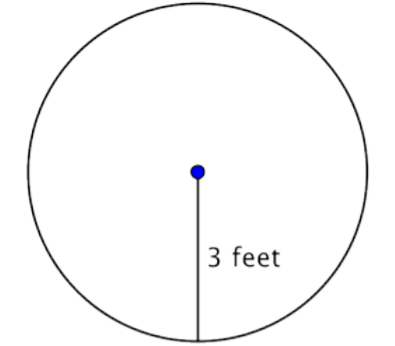
Solution
To find the area of this circle, use the formula \(A = \pi r^2\). Remember to write the answer in terms of square units, since you are finding the area.
\(A = \pi r^2\)
\(A = \pi \cdot 3^2\)
\(A = \pi \cdot 9\)
\(A = 3.14 \cdot 9\)
\(A = 28.26\)
Answer The area is \(9\pi\) or approximately \(28.26 \text{ feet}^2\).
Try It Now 2
A button has a diameter of 20 millimeters. What is the area of the button? Use 3.14 as an approximation of \(\pi\).
Composite Figures
Now that you know how to calculate the circumference and area of a circle, you can use this knowledge to find the perimeter and area of composite figures. The trick to figuring out these types of problems is to identify shapes (and parts of shapes) within the composite figure, calculate their individual dimensions, and then add them together.
For example, look at the image below. Is it possible to find the perimeter?
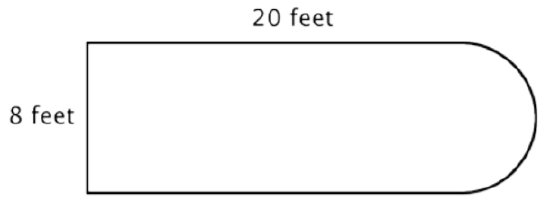
The first step is to identify simpler figures within this composite figure. You can break it down into a rectangle and a semicircle, as shown below.
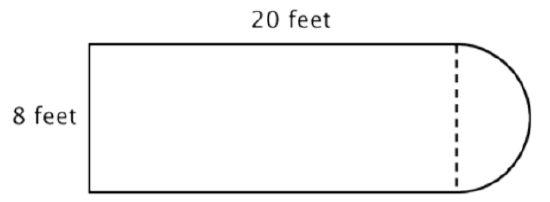
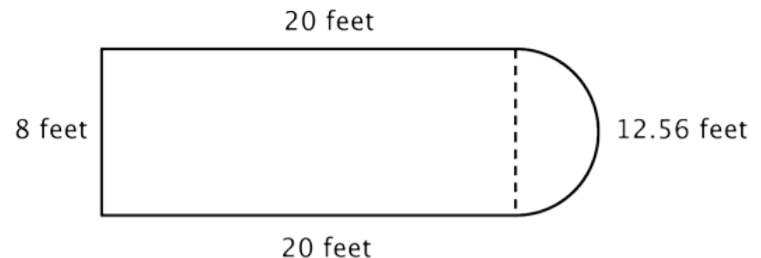
You know how to find the perimeter of a rectangle, and you know how to find the circumference of a circle. Here, the perimeter of the three solid sides of the rectangle is 8 + 20 + 20 = 48 feet. (Note that only three sides of the rectangle will add into the perimeter of the composite figure because the other side is not at an edge; it is covered by the semicircle!)
To find the circumference of the semicircle, use the formula \(C = \pi d\) with a diameter of 8 feet, then take half of the result. The circumference of the semicircle is \(4 \pi\), or approximately 12.56 feet, so the total perimeter is about 60.56 feet.
Example \(\PageIndex{17}\)
Find the perimeter (to the nearest hundredth) of the composite figure, made up of a semi-circle and a triangle.
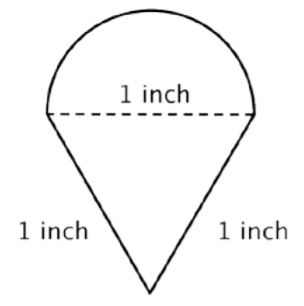
Solution
Identify smaller shapes within the composite figure. This figure contains a semicircle and a triangle.
Find the circumference of the circle. Then divide by 2 to find the circumference of the semi-circle.
\(\text{Diameter }(d) = 1\)
\(C = \pi d\)
\(C = \pi (1)\)
\(C = \pi\)
\(\text{Circumference of semicircle } = \dfrac{1}{2} \pi\) or approximately \(1.57 \text{ inches}\)
Find the total perimeter by adding the circumference of the semicircle and the lengths of the two legs. Since our measurement of the semicircle’s circumference is approximate, the perimeter will be an approximation also.
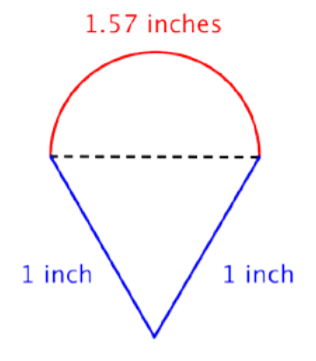
\(1 + 1 + \dfrac{1}{2} \pi ≈ 3.57 \text{ inches}\)
Recall, we use the original units with perimeter.
Answer: Approximately \(3.57 \text{ inches}\)
Example \(\PageIndex{18}\)
Find the area of the composite figure, made up of three-quarters of a circle and a square, to the nearest hundredth.
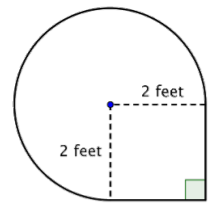
Solution
Identify smaller shapes within the composite figure. This figure contains a circular region and a square. If you find the area of each, you can find the area of the entire figure.
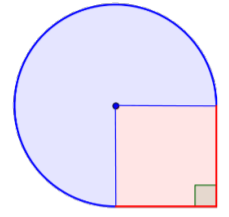
Find the area of the square.
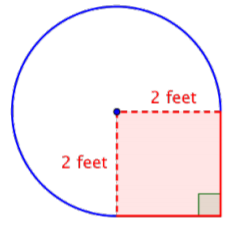
\(\text{Area of square} = s^2\)
\(= (2)^2\)
\(= 4 \text{ ft}^2\)
Find the area of the circular region. The radius is \(2 \text{ feet}\).
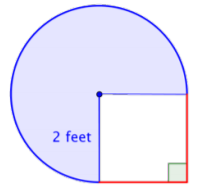
Note that the region is \(\dfrac{3}{4}\) of a whole circle, so you need to multiply the area of the circle by \(\dfrac{3}{4}\). Use 3.14 as an approximation for \(\pi\).
\(\text{Area of full circle} = \pi r^2\)
\(= \pi (2)^2\)
\(= 4 \pi \text{ ft}^2\)
\(\text{Area of region} = \dfrac{3}{4} \cdot 4 \pi \)
\(= 3 \pi\)
\(≈ 3 \cdot 3.14 \text{ ft}^2\)
This is approximately \(9.42 \text{ feet}^2\).
Add the two regions together. Since your measurement of the circular’s area is approximate, the area of the figure will be an approximation also.
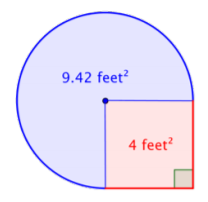
\(4 \text{ feet}^2 + 3 \pi \text{ feet}^2 =\) approximately \(13.42 \text{ feet}^2\)
Recall, we use square units for area.
Answer: The area is approximately \(13.42 \text{ feet}^2\).
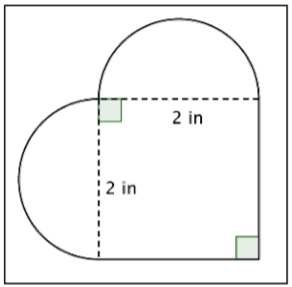
Try It Now 3
What is the area (to the nearest hundredth) of the figure shown below? (Both rounded regions are semi-circles.)
Summary
Circles are an important geometric shape. The distance around a circle is called the circumference, and the interior space of a circle is called the area. Calculating the circumference and area of a circle requires a number called pi (\(\pi\)), which is a non-terminating, non-repeating decimal. Pi is often approximated by the values 3.14 and \(\dfrac{22}{7}\). You can find the perimeter or area of composite shapes—including shapes that contain circular sections—by applying the circumference and area formulas where appropriate.
Try It Now Answers
- \(50 \text{ inches}\); if the radius is \(8 \text{ inches}\), the correct formula for circumference when the radius is given is \(C = 2 \pi r\). The correct answer is \(50 \text{ inches}\).
- \(314 \text{ mm}^2\); the diameter is \(20 \text{ mm}\), so the radius must be \(10 \text{ mm}\). Then, using the formula \(A = \pi r^2\), you find \(A = \pi \cdot 10^2 = \pi \cdot 100 ≈ 314 \text{ mm}^2\).
- \(7.14 \text{ in}^2\); imagine the two semi-circles being put together to create one circle. The radius of the circle is \(1 \text{ inch}\); this means the area of the circle is \(\pi r^2 = \pi \cdot 1^2 = \pi\). The area of the square is \(2 \cdot 2 = 4\). Adding those together yields \(7.14 \text{ in}^2\).


