11.1: Voting Methods
- Page ID
- 87367
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
A preference ballot is a ballot in which voters rank their choices in order.
Here are four methods to determine which candidate is the winner of an election.
In this method, the candidate with the most first place votes is declared the winner.
This method is sometimes mistakenly called the majority method, or “majority rules”, but it is not necessary for a choice to have gained a majority of votes to win. A majority is over 50%; it is possible for a winner to have a plurality without having a majority.
In our election from previous pages, we had the preference table:
\(\begin{array}{|l|l|l|l|l|}
\hline & 1 & 3 & 3 & 3 \\
\hline 1^{\text {st }} \text { choice } & \text { A } & \text { A } & \text { O } & \text { H } \\
\hline 2^{\text {nd }} \text { choice } & \text { O } & \text { H } & \text { H } & \text { A } \\
\hline 3^{\text {rd }} \text { choice } & \text { H } & \text { O } & \text { A } & \text { O } \\
\hline
\end{array}\)
Solution
For the plurality method, we only care about the first choice options. Totaling them up:
Anaheim: 1+3 = 4 first-choice votes
Orlando: 3 first-choice votes
Hawaii: 3 first-choice votes
Anaheim is the winner using the plurality voting method.
Notice that Anaheim won with 4 out of 10 votes, 40% of the votes, which is a plurality of the votes, but not a majority.
Three candidates are running in an election for County Executive: Goings (G), McCarthy (M), and Bunney (B)[1]. The voting schedule is shown below. Which candidate wins under the Plurality Method?
\(\begin{array}{|l|l|l|l|l|}
\hline & 44 & 14 & 20 & 70 & 22 & 80 & 39 \\
\hline 1^{\text {st }} \text { choice } & \text { G } & \text { G } & \text { G } & \text { M } & \text { M } & \text { B } & \text { B } \\
\hline 2^{\text {nd }} \text { choice } & \text { M } & \text { B } & \text { } & \text { G } & \text { B } & \text { M } & \text { } \\
\hline 3^{\text {rd }} \text { choice } & \text { B } & \text { M } & \text { } & \text { B } & \text { G } & \text { G } & \text { } \\
\hline
\end{array}\)
Note: In the third column and last column, those voters only recorded a first-place vote, so we don’t know who their second and third choices would have been.
- Answer
-
Using plurality method:
G gets \(44+14+20 = 78\) first-choice votes
M gets \(70+22 = 92\) first-choice votes
B gets \(80+39 = 119\) first-choice votes
Bunney (B) wins under Plurality Method.
Plurality with Elimination is a modification of the plurality method.
In this method, the candidate with the least first-place votes is then eliminated from the election, and any votes for that candidate are redistributed to the voters’ next choice. This continues until a candidate has a majority (over 50%).
This is similar to the idea of holding runoff elections, but since every voter’s order of preference is recorded on the ballot, the runoff can be computed without requiring a second costly election.
This voting method is used in several political elections around the world, including election of members of the Australian House of Representatives, and was used for county positions in Pierce County, Washington until it was eliminated by voters in 2009. A version of IRV is used by the International Olympic Committee to select host nations.
Consider the preference schedule below, in which a company’s advertising team is voting on five different advertising slogans, called A, B, C, D, and E here for simplicity.
Initial votes
\(\begin{array}{|l|l|l|l|l|l|l|}
\hline & 3 & 4 & 4 & 6 & 2 & 1 \\
\hline 1^{\text {st choice }} & \mathrm{B} & \mathrm{C} & \mathrm{B} & \mathrm{D} & \mathrm{B} & \mathrm{E} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{C} & \mathrm{A} & \mathrm{D} & \mathrm{C} & \mathrm{E} & \mathrm{A} \\
\hline 3^{\text {rd }} \text { choice } & \mathrm{A} & \mathrm{D} & \mathrm{C} & \mathrm{A} & \mathrm{A} & \mathrm{D} \\
\hline 4^{\text {th }} \text { choice } & \mathrm{D} & \mathrm{B} & \mathrm{A} & \mathrm{E} & \mathrm{C} & \mathrm{B} \\
\hline 5^{\text {th }} \text { choice } & \mathrm{E} & \mathrm{E} & \mathrm{E} & \mathrm{B} & \mathrm{D} & \mathrm{C} \\
\hline
\end{array}\)
If this was a plurality election, note that B would be the winner with 9 first-choice votes, compared to 6 for D, 4 for C, and 1 for E.
There are total of 3+4+4+6+2+1 = 20 votes. A majority would be 11 votes. No one yet has a majority, so we proceed to elimination rounds.
Solution
Round 1: We make our first elimination. Choice A has the fewest first-place votes, so we remove that choice
\(\begin{array}{|l|l|l|l|l|l|l|}
\hline & 3 & 4 & 4 & 6 & 2 & 1 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{B} & \mathrm{C} & \mathrm{B} & \mathrm{D} & \mathrm{B} & \mathrm{E} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{C} & & \mathrm{D} & \mathrm{C} & \mathrm{E} & \\
\hline 3^{\text {rd }} \text { choice } & & \mathrm{D} & \mathrm{C} & & & \mathrm{D} \\
\hline 4^{\text {th }} \text { choice } & \mathrm{D} & \mathrm{B} & & \mathrm{E} & \mathrm{C} & \mathrm{B} \\
\hline 5^{\text {th }} \text { choice } & \mathrm{E} & \mathrm{E} & \mathrm{E} & \mathrm{B} & \mathrm{D} & \mathrm{C} \\
\hline
\end{array}\)
We then shift everyone’s choices up to fill the gaps. There is still no choice with a majority, so we eliminate again.
\(\begin{array}{|l|l|l|l|l|l|l|}
\hline & 3 & 4 & 4 & 6 & 2 & 1 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{B} & \mathrm{C} & \mathrm{B} & \mathrm{D} & \mathrm{B} & \mathrm{E} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{C} & \mathrm{D} & \mathrm{D} & \mathrm{C} & \mathrm{E} & \mathrm{D} \\
\hline 3^{\text {rd }} \text { choice } & \mathrm{D} & \mathrm{B} & \mathrm{C} & \mathrm{E} & \mathrm{C} & \mathrm{B} \\
\hline 4^{\text {th }} \text { choice } & \mathrm{E} & \mathrm{E} & \mathrm{E} & \mathrm{B} & \mathrm{D} & \mathrm{C} \\
\hline
\end{array}\)
Round 2: We make our second elimination. Choice E has the fewest first-place votes, so we remove that choice, shifting everyone’s options to fill the gaps.
\(\begin{array}{|l|l|l|l|l|l|l|}
\hline & 3 & 4 & 4 & 6 & 2 & 1 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{B} & \mathrm{C} & \mathrm{B} & \mathrm{D} & \mathrm{B} & \mathrm{D} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{C} & \mathrm{D} & \mathrm{D} & \mathrm{C} & \mathrm{C} & \mathrm{B} \\
\hline 3^{\text {rd }} \text { choice } & \mathrm{D} & \mathrm{B} & \mathrm{C} & \mathrm{B} & \mathrm{D} & \mathrm{C} \\
\hline
\end{array}\)
Notice that the first and fifth columns have the same preferences now, we can condense those down to one column.
\(\begin{array}{|l|l|l|l|l|l|}
\hline & 5 & 4 & 4 & 6 & 1 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{B} & \mathrm{C} & \mathrm{B} & \mathrm{D} & \mathrm{D} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{C} & \mathrm{D} & \mathrm{D} & \mathrm{C} & \mathrm{B} \\
\hline 3^{\text {rd }} \text { choice } & \mathrm{D} & \mathrm{B} & \mathrm{C} & \mathrm{B} & \mathrm{C} \\
\hline
\end{array}\)
Now B has 9 first-choice votes, C has 4 votes, and D has 7 votes. Still no majority, so we eliminate again.
Round 3: We make our third elimination. C has the fewest votes.
\(\begin{array}{|l|l|l|l|l|l|}
\hline & 5 & 4 & 4 & 6 & 1 \\
\hline 1^{\text {st }} \text { choice } & \text { B } & \text { D } & \text { B } & \text { D } & \text { D } \\
\hline 2^{\text {nd }} \text { choice } & \text { D } & \text { B } & \text { D } & \text { B } & \text { B } \\
\hline
\end{array}\)
Condensing this down:
\(\begin{array}{|l|l|l|}
\hline & 9 & 11 \\
\hline 1^{\text {st }} \text { choice } & \text { B } & \text { D } \\
\hline 2^{\text {nd }} \text { choice } & \text { D } & \text { B } \\
\hline
\end{array}\)
D has now gained a majority, and is declared the winner under Plurality with Elimination.
Consider again the election from Try it Now 1. Find the winner using Plurality with Elimination.
\(\begin{array}{|l|l|l|l|l|l|l|l|}
\hline & 44 & 14 & 20 & 70 & 22 & 80 & 39 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{G} & \mathrm{G} & \mathrm{G} & \mathrm{M} & \mathrm{M} & \mathrm{B} & \mathrm{B} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{M} & \mathrm{B} & & \mathrm{G} & \mathrm{B} & \mathrm{M} & \\
\hline 3^{\text {rd }} \text { choice } & \mathrm{B} & \mathrm{M} & & \mathrm{B} & \mathrm{G} & \mathrm{G} & \\
\hline
\end{array}\)
- Answer
-
G has the fewest first-choice votes, so is eliminated first. The 20 voters who did not list a second choice do not get transferred - they simply get eliminated
\(\begin{array}{|l|l|l|}
\hline & 136 & 133 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{M} & \mathrm{B} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{B} & \mathrm{M} \\
\hline
\end{array}\)McCarthy (M) now has a majority, and is declared the winner.
Borda Count is another voting method, named for Jean-Charles de Borda, who developed the system in 1770.
In this method, points are assigned to candidates based on their ranking; 1 point for last choice, 2 points for second-to-last choice, and so on. The point values for all ballots are totaled, and the candidate with the largest point total is the winner.
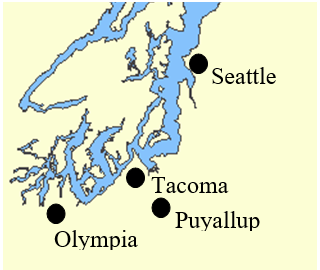A group of mathematicians are getting together for a conference. The members are coming from four cities: Seattle, Tacoma, Puyallup, and Olympia. Their approximate locations on a map are shown to the right.
The votes for where to hold the conference were:
\(\begin{array}{|l|l|l|l|l|}
\hline & 51 & 25 & 10 & 14 \\
\hline 1^{\text {st }} \text { choice } & \text { Seattle } & \text { Tacoma } & \text { Puyallup } & \text { Olympia } \\
\hline 2^{\text {nd }} \text { choice } & \text { Tacoma } & \text { Puyallup } & \text { Tacoma } & \text { Tacoma } \\
\hline 3^{\text {rd }} \text { choice } & \text { Olympia } & \text { Olympia } & \text { Olympia } & \text { Puyallup } \\
\hline 4^{\text {th }} \text { choice } & \text { Puyallup } & \text { Seattle } & \text { Seattle } & \text { Seattle } \\
\hline
\end{array}\)
Solution
In each of the 51 ballots ranking Seattle first, Puyallup will be given 1 point, Olympia 2 points, Tacoma 3 points, and Seattle 4 points. Multiplying the points per vote times the number of votes allows us to calculate points awarded:
\(\begin{array}{|l|l|l|l|l|}
\hline & 51 & 25 & 10 & 14 \\
\hline 1^{\text {st choice }} & \text { Seattle } & \text { Tacoma } & \text { Puyallup } & \text { Olympia } \\
4 \text { points } & 4 \cdot 51=204 & 4 \cdot 25= 100 & 4 \cdot 10=40 & 4 \cdot 14=56 \\
\hline 2^{\text {nd choice }} & \text { Tacoma } & \text { Puyallup } & \text { Tacoma } & \text { Tacoma } \\
3 \text { points } & 3 \cdot 51=153 & 3 \cdot 25=75 & 3 \cdot 10=30 & 3 \cdot 14=42 \\
\hline 3^{\text {rd }} \text { choice } & \text { Olympia } & \text { Olympia } & \text { Olympia } & \text { Puyallup } \\
2 \text { points } & 2 \cdot 51=102 & 2 \cdot 25=50 & 2 \cdot 10=20 & 2 \cdot 14=28 \\
\hline 4^{\text {th }} \text { choice } & \text { Puyallup } & \text { Seattle } & \text { Seattle } & \text { Seattle } \\
1 \text { point } & 1 \cdot 51=51 & 1 \cdot 25=25 & 1 \cdot 10=10 & 1 \cdot 14=14 \\
\hline
\end{array}\)
Adding up the points:
- Seattle: \(204 + 25 + 10 + 14 = 253\) points
- Tacoma: \(153 + 100 + 30 + 42 = 325\) points
- Puyallup: \(51 + 75 + 40 + 28 = 194\) points
- Olympia: \(102 + 50 + 20 + 56 = 228\) points
Under the Borda Count method, Tacoma is the winner of this vote.
Consider again the election from Try it Now 1. Find the winner using Borda Count. Since we have some incomplete preference ballots, for simplicity, give every unranked candidate 1 point, the points they would normally get for last place.
\(\begin{array}{|l|l|l|l|l|l|l|l|}
\hline & 44 & 14 & 20 & 70 & 22 & 80 & 39 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{G} & \mathrm{G} & \mathrm{G} & \mathrm{M} & \mathrm{M} & \mathrm{B} & \mathrm{B} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{M} & \mathrm{B} & & \mathrm{G} & \mathrm{B} & \mathrm{M} & \\
\hline 3^{\text {rd }} \text { choice } & \mathrm{B} & \mathrm{M} & & \mathrm{B} & \mathrm{G} & \mathrm{G} & \\
\hline
\end{array}\)
- Answer
-
Using Borda Count:
We give 1 point for 3rd place, 2 points for 2nd place, and 3 points for 1st place.
\(\begin{array}{|l|l|l|l|l|l|l|l|}
\hline & 44 & 14 & 20 & 70 & 22 & 80 & 39 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{G} & \mathrm{G} & \mathrm{G} & \mathrm{M} & \mathrm{M} & \mathrm{B} & \mathrm{B} \\
& 132 \mathrm{pt} & 42 \mathrm{pt} & 60 \mathrm{pt} & 210 \mathrm{pt} & 66 \mathrm{pt} & 240 \mathrm{pt} & 117 \mathrm{pt} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{M} & \mathrm{B} & & \mathrm{G} & \mathrm{B} & \mathrm{M} & \\
& 88 \mathrm{pt} & 28 \mathrm{pt} & & 140 \mathrm{pt} & 44 \mathrm{pt} & 160 \mathrm{pt} & \\
\hline 3^{\text {rd }} \text { choice } & \mathrm{B} & \mathrm{M} & \mathrm{M} 20 \mathrm{pt} & \mathrm{B} & \mathrm{G} & \mathrm{G} & \mathrm{M} 39 \mathrm{pt} \\
& 44 \mathrm{pt} & 14 \mathrm{pt} & \mathrm{B} 20 \mathrm{pt} & 70 \mathrm{pt} & 22 \mathrm{pt} & 80 \mathrm{pt} & \mathrm{G} 39 \mathrm{pt} \\
\hline
\end{array}\)G: \(132+42+60+140+22+80+39 = 515\) pts
M: \(88+14+20+210+66+160+39 = 597\) pts
B: \(44+28+20+70+44+240+117 = 563\) pts
McCarthy (M) would be the winner using Borda Count.
The fourth method is the Pairwise Comparison Method.
In this method, each pair of candidates is compared, using all preferences to determine which of the two is more preferred. The more preferred candidate is awarded 1 point. If there is a tie, each candidate is awarded \(\frac{1}{2}\) point. After all pairwise comparisons are made, the candidate with the most points, and hence the most pairwise wins, is declared the winner.
Consider our vacation group example from the beginning of the chapter. Determine the winner using Pairwise Comparison Method.
\(\begin{array}{|l|l|l|l|l|}
\hline & 1 & 3 & 3 & 3 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{A} & \mathrm{A} & \mathrm{O} & \mathrm{H} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{O} & \mathrm{H} & \mathrm{H} & \mathrm{A} \\
\hline 3^{\text {rd }} \text { choice } & \mathrm{H} & \mathrm{O} & \mathrm{A} & \mathrm{O} \\
\hline
\end{array}\)
Solution
We need to look at each pair of choices, and see which choice would win in a one-to-one comparison. For example, comparing Hawaii vs Orlando, we see that 6 voters, those shaded below in the first table below, would prefer Hawaii to Orlando. Note that Hawaii doesn’t have to be the voter’s first choice – we’re imagining that Anaheim wasn’t an option. If it helps, you can imagine removing Anaheim, as in the second table below.
Based on this, in the comparison of Hawaii vs Orlando, Hawaii wins, and receives 1 point.
Comparing Anaheim to Orlando, the 1 voter in the first column clearly prefers Anaheim, as do the 3 voters in the second column. The 3 voters in the third column clearly prefer Orlando. The 3 voters in the last column prefer Hawaii as their first choice, but if they had to choose between Anaheim and Orlando, they'd choose Anaheim, their second choice overall. So, altogether 1+3+3=7 voters prefer Anaheim over Orlando, and 3 prefer Orlando over Anaheim. So, comparing Anaheim vs Orlando: 7 votes to 3 votes: Anaheim gets 1 point.
All together,
\(\begin{array} {ll} {\text{Hawaii vs Orlando: }} & {6\text{ votes to }4\text{ votes: Hawaii gets }1\text{ point}} \\ {\text{Anaheim vs Orlando:}} & {7\text{ votes to }3\text{ votes: Anaheim gets }1\text{ point}} \\ {\text{Hawaii vs Anaheim: }} & {6\text{ votes to }4\text{ votes: Hawaii gets }1\text{ point}} \end{array}\)
Hawaii is the winner under Pairwise Comparison Method, having earned the most points.
Consider the advertising group’s vote we explored earlier. Determine the winner using Pairwise Comparison Method.
\(\begin{array}{|l|l|l|l|l|l|l|}
\hline & 3 & 4 & 4 & 6 & 2 & 1 \\
\hline 1^{\text {st }} \text { choice } & \text { B } & \text { C } & \text { B } & \text { D } & \text { B } & \text { E } \\
\hline 2^{\text {nd }} \text { choice } & \text { C } & \text { A } & \text { D } & \text { C } & \text { E } & \text { A } \\
\hline 3^{\text {rd }} \text { choice } & \text { A } & \text { D } & \text { C } & \text { A } & \text { A } & \text { D } \\
\hline 4^{\text {th }} \text { choice } & \text { D } & \text { B } & \text { A } & \text { E } & \text { C } & \text { B } \\
\hline 5^{\text {th }} \text { choice } & \text { E } & \text { E } & \text { E } & \text { B } & \text { D } & \text { C } \\
\hline
\end{array}\)
Solution
With 5 candidates, there are 10 comparisons to make:
\( \begin{array} {ll} {\text{A vs B: }11\text{ votes to }9\text{ votes}} & {\text{A gets }1\text{ point}} \\ {\text{A vs C: }3\text{ votes to }17\text{ votes}} & {\text{C gets }1\text{ point}} \\ {\text{A vs D: }10\text{ votes to }10\text{ votes }} & {\text{A gets }\frac{1}{2}\text{ point, D gets }\frac{1}{2}\text{ point}} \\ {\text{A vs E: }17\text{ votes to }3\text{ votes}} & {\text{A gets }1\text{ point}} \\ {\text{B vs C: }10\text{ votes to }10\text{ votes}} & {\text{B gets }\frac{1}{2}\text{ point, C gets }\frac{1}{2}\text{ point}} \\ {\text{B vs D: }9\text{ votes to }11\text{ votes}} & {\text{D gets }1\text{ point}} \\ {\text{B vs E: }13\text{ votes to }7\text{ votes}} & {\text{B gets }1\text{ point}} \\ {\text{C vs D: }9\text{ votes to }11\text{ votes}} & {\text{D gets }1\text{ point}} \\ {\text{C vs E: }17\text{ votes to }3\text{ votes}} & {\text{C gets }1\text{ point}} \\ {\text{D vs E: }17\text{ votes to }3\text{ votes}} & {\text{D gets }1\text{ point}} \end{array}\)
Totaling these up:
A gets \(2\frac{1}{2}\) points
B gets \(1\frac{1}{2}\) points
C gets \(2\frac{1}{2}\) points
D gets \(3\frac{1}{2}\) points
E gets \(0\) points
Using Pairwise Comparison Method, we declare D as the winner.
Consider again the election from Try it Now 1. Find the winner using Pairwise Comparison method. Since we have some incomplete preference ballots, we’ll have to adjust. For example, when comparing M to B, we’ll ignore the 20 votes in the third column which do not rank either candidate.
\(\begin{array}{|l|l|l|l|l|l|l|l|}
\hline & 44 & 14 & 20 & 70 & 22 & 80 & 39 \\
\hline 1^{\text {st }} \text { choice } & \mathrm{G} & \mathrm{G} & \mathrm{G} & \mathrm{M} & \mathrm{M} & \mathrm{B} & \mathrm{B} \\
\hline 2^{\text {nd }} \text { choice } & \mathrm{M} & \mathrm{B} & & \mathrm{G} & \mathrm{B} & \mathrm{M} & \\
\hline 3^{\text {rd }} \text { choice } & \mathrm{B} & \mathrm{M} & & \mathrm{B} & \mathrm{G} & \mathrm{G} & \\
\hline
\end{array}\)
- Answer
-
Using Pairwise Comparison Method:
Looking back at our work from Try it Now #2, we see
G vs M: \(44+14+20 = 78\) prefer G, \(70+22+80=172\) prefer M: M preferred – 1 point
G vs B: \(44+14+20+70=148\) prefer G, \(22+80+39 = 141\) prefer B: G preferred – 1 point
M vs B: \(44+70+22=136\) prefer M, \(14+80+39=133\) prefer B: M preferred – 1 point
M earns 2 points; G earns 1 point. M wins under Pairwise Comparison Method.
[1] This data is loosely based on the 2008 County Executive election in Pierce County, Washington. See www.co.pierce.wa.us/xml/abtus...ec/summary.pdf