Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

9.1: Simplify and Use Square Roots

  1. Last updated
  2. Save as PDF
  • Page ID
    18987

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    By the end of this section, you will be able to:
    • Simplify expressions with square roots
    • Estimate square roots
    • Approximate square roots
    • Simplify variable expressions with square roots

    Before you get started, take this readiness quiz.

    1. Simplify: ⓐ \(9^2\) ⓑ \((−9)^2\) ⓒ \(−9^2\).
      If you missed this problem, review [link].
    2. Round 3.846 to the nearest hundredth.
      If you missed this problem, review [link].
    3. For each number, identify whether it is a real number or not a real number:
      ⓐ \(−\sqrt{100}\) ⓑ \(\sqrt{−100}\).
      If you missed this problem, review [link].

    Simplify Expressions with Square Roots

    Remember that when a number n is multiplied by itself, we write \(n^2\) and read it “n squared.” For example, \(15^2\) reads as “15 squared,” and 225 is called the square of 15, since \(15^2=225\).

    Definition: SQUARE OF A NUMBER

    If \(n^2=m\), then m is the square of n.

    Sometimes we will need to look at the relationship between numbers and their squares in reverse. Because 225 is the square of 15, we can also say that 15 is a square root of 225. A number whose square is m is called a square root of m.

    Definition: SQUARE ROOT OF A NUMBER

    If \(n^2=m\), then n is a square root of m.

    Notice \((−15)^2=225\) also, so −15 is also a square root of 225. Therefore, both 15 and −15 are square roots of 225.

    So, every positive number has two square roots—one positive and one negative. What if we only wanted the positive square root of a positive number? The radical sign, \(\sqrt{m}\), denotes the positive square root. The positive square root is also called the principal square root.

    We also use the radical sign for the square root of zero. Because \(0^2=0\), \(\sqrt{0}=0\). Notice that zero has only one square root.

    Definition: SQUARE ROOT NOTATION

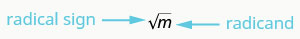
    This figure is a picture of an m inside a square root sign. The sign is labeled as a radical sign and the m is labeled as the radicand.

    \(\sqrt{m}\) is read as “the square root of m.”

    If \(m=n^2\), then \(\sqrt{m}=n\), for \(n \ge 0\).

    The square root of m, \(\sqrt{m}\), is the positive number whose square is m.

    Since 15 is the positive square root of 225, we write \(\sqrt{225}=15\). Fill in Figure to make a table of square roots you can refer to as you work this chapter.

    This table has fifteen columns and two rows. The first row contains the following numbers: the square root of 1, the square root of 4, the square root of 9, the square root of 16, the square root of 25, the square root of 36, the square root of 49, the square root of 64, the square root of 81, the square root of 100, the square root of 121, the square root of 144, the square root of 169, the square root of 196, and the square root of 225. The second row is completely empty except for the last column. The number 15 is in the last column.

    We know that every positive number has two square roots and the radical sign indicates the positive one. We write \(\sqrt{225}=15\). If we want to find the negative square root of a number, we place a negative in front of the radical sign. For example, \(−\sqrt{225}=−15\).

    Example \(\PageIndex{1}\)

    Simplify:

    1. \(\sqrt{36}\)
    2. \(\sqrt{196}\)
    3. \(−\sqrt{81}\)
    4. \(−\sqrt{289}\).
    Answer

    1.
    \[\begin{array}{ll} {}&{\sqrt{36}}\\ {\text{Since} 6^2=36}&{6}\\ \end{array}\]
    2.
    \[\begin{array}{ll} {}&{\sqrt{196}}\\ {\text{Since} 14^2=196}&{14}\\ \end{array}\]
    3.
    \[\begin{array}{ll} {}&{−\sqrt{81}}\\ {\text{The negative is in front of the radical sign}}&{−9}\\ \end{array}\]
    4.
    \[\begin{array}{ll} {}&{−\sqrt{289}}\\ {\text{The negative is in front of the radical sign}}&{−17}\\ \end{array}\]

    Example \(\PageIndex{2}\)

    Simplify:

    1. \(−\sqrt{49}\)
    2. \(\sqrt{225}\).
    Answer
    1. −7
    2. 15

    Example \(\PageIndex{3}\)

    implify:

    1. \(\sqrt{64}\)
    2. \(−\sqrt{121}\).
    Answer
    1. 8
    2. −11

    Example \(\PageIndex{4}\)

    Simplify:

    1. \(\sqrt{−169}\)
    2. \( −\sqrt{64}\)
    Answer

    1.

    \[\begin{array}{ll} {}&{\sqrt{−169}}\\ {\text{There is no real number whose square is} s−169}&{\sqrt{−169} \text{is not a real number.}}\\ \end{array}\]

    2.

    \[\begin{array}{ll} {}&{−\sqrt{64}}\\ {\text{The negative is in front of the radical sign}}&{−8}\\ \end{array}\]

    Example \(\PageIndex{5}\)

    Simplify:

    1. \(\sqrt{−196}\)
    2. \(−\sqrt{81}\).
    Answer
    1. not a real number
    2. −9

    Example \(\PageIndex{6}\)

    Simplify:

    1. \(−\sqrt{49}\)
    2. \(\sqrt{ −121}\).
    Answer
    1. −7
    2. not a real number

    ​​​​​​​When using the order of operations to simplify an expression that has square roots, we treat the radical as a grouping symbol.

    Example \(\PageIndex{7}\)

    Simplify:

    1. \(\sqrt{25} +\sqrt{144}\)
    2. \(\sqrt{25+144}\).
    Answer

    1.

    \[\begin{array}{ll} {}&{\sqrt{25} +\sqrt{144}}\\ {\text{Use the order of operations}}&{5+12}\\ {\text{Simplify.}}&{17}\\ \end{array}\]

    2.

    \[\begin{array}{ll} {}&{\sqrt{25+144}}\\ {\text{Simplify under the radical sign.}}&{\sqrt{169}}\\ {\text{Simplify.}}&{13}\\ \end{array}\]

    Notice the different answers in parts 1 and 2!

    Example \(\PageIndex{8}\)

    Simplify:

    1. \(\sqrt{9}+\sqrt{16}\)
    2. \(\sqrt{9+16}\).
    Answer
    1. 7
    2. 5

    Example \(\PageIndex{9}\)

    Simplify:

    1. \(\sqrt{64+225}\)
    2. \(\sqrt{64}+\sqrt{225}\).
    Answer
    1. 17
    2. 23

    Estimate Square Roots

    So far we have only considered square roots of perfect square numbers. The square roots of other numbers are not whole numbers. Look at Table below.

    Number Square Root
    4 \(\sqrt{4}=2\)
    5 \(\sqrt{5}\)
    6 \(\sqrt{6}\)
    7 \(\sqrt{7}\)
    8 \(\sqrt{8}\)
    9 \(\sqrt{9}=3\)

    The square roots of numbers between 4 and 9 must be between the two consecutive whole numbers 2 and 3, and they are not whole numbers. Based on the pattern in the table above, we could say that \(\sqrt{5}\) must be between 2 and 3. Using inequality symbols, we write:

    \(2<\sqrt{5}<3\)

    Example \(\PageIndex{10}\)

    Estimate \(\sqrt{60}\) between two consecutive whole numbers.

    Answer

    Think of the perfect square numbers closest to 60. Make a small table of these perfect squares and their squares roots.

    .
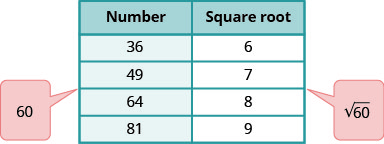
    Locate 60 between two consecutive perfect squares. .
    \(\sqrt{60}\) is between their square roots. .

    Example \(\PageIndex{11}\)

    Estimate the square root \(\sqrt{38}\) between two consecutive whole numbers.

    Answer

    \(6<\sqrt{38}<7\)

    Example \(\PageIndex{12}\)

    Estimate the square root \(\sqrt{84}\) between two consecutive whole numbers.

    Answer

    \(9<\sqrt{84}<10\)

    Approximate Square Roots

    There are mathematical methods to approximate square roots, but nowadays most people use a calculator to find them. Find the \(\sqrt{x}\) key on your calculator. You will use this key to approximate square roots.

    When you use your calculator to find the square root of a number that is not a perfect square, the answer that you see is not the exact square root. It is an approximation, accurate to the number of digits shown on your calculator’s display. The symbol for an approximation is \(\approx\) and it is read ‘approximately.’

    Suppose your calculator has a 10-digit display. You would see that

    \(\sqrt{5} \approx 2.236067978\)

    If we wanted to round \(\sqrt{5}\) to two decimal places, we would say

    \(\sqrt{5} \approx 2.24\)

    How do we know these values are approximations and not the exact values? Look at what happens when we square them:

    \[\begin{array}{c} {(2.236067978)^2=5.000000002}\\ {(2.24)^2=5.0176}\\ \end{array}\]

    Their squares are close to 5, but are not exactly equal to 5.

    Using the square root key on a calculator and then rounding to two decimal places, we can find:

    \[\begin{array}{c} {\sqrt{4}=2}\\ {\sqrt{5} \approx 2.24}\\ {\sqrt{6} \approx 2.45}\\ {\sqrt{7} \approx 2.65}\\ {\sqrt{8} \approx 2.83}\\ {\sqrt{9}=3}\\ \end{array}\]

    Example \(\PageIndex{13}\)

    Round \(\sqrt{17}\) to two decimal places.

    Answer

    \[\begin{array}{ll} {}&{\sqrt{17}}\\ {\text{Use the calculator square root key.}}&{4.123105626...}\\ {\text{Round to two decimal places.}}&{4.12}\\ {}&{\sqrt{17} \approx 4.12} \end{array}\]

    Example \(\PageIndex{14}\)

    Round \(\sqrt{11}\) to two decimal places.

    Answer

    \(\approx 3.32\)

    Example \(\PageIndex{15}\)

    Round \(\sqrt{13}\) to two decimal places.

    Answer

    \(\approx 3.61\)

    Simplify Variable Expressions with Square Roots

    What if we have to find a square root of an expression with a variable? Consider \(\sqrt{9x^2}\). Can you think of an expression whose square is \(9x^2\)?

    \[\begin{array}{cc} {(?)^2=9x^2}&{}\\ {(3x)^2=9x^2}&{\text{so} \sqrt{9x^2}=3x}\\ \end{array}\]

    When we use the radical sign to take the square root of a variable expression, we should specify that x≥0x≥0 to make sure we get the principal square root.

    However, in this chapter we will assume that each variable in a square-root expression represents a non-negative number and so we will not write \(x \ge 0\) next to every radical.

    What about square roots of higher powers of variables? Think about the Power Property of Exponents we used in Chapter 6.

    \((a^m)^n=a^{m·n}\)

    If we square \(a^m\), the exponent will become 2m.

    \((a^m)^2=a^{2m}\)

    How does this help us take square roots? Let’s look at a few:

    \[\begin{array}{cc} {\sqrt{25u^8}=5u^4}&{\text{Because} (5u^4)^2=25u^8}\\ {\sqrt{16r^{20}}=4r^{10}}&{\text{Because} (4r^{10})^2=16r^{20}}\\ {\sqrt{196q^{36}}=14q^{18}}&{\text{Because} (14r^{18})^2=196q^{36}}\\ \end{array}\]

    Example \(\PageIndex{16}\)

    Simplify:

    1. \(\sqrt{x^6}\)
    2. \(\sqrt{y^{16}}\)
    Answer

    1.

    \[\begin{array}{ll} {}&{\sqrt{x^6}}\\ {\text{Since} (x^3)^2=x^6}&{x^3}\\ \end{array}\]

    2.

    \[\begin{array}{ll} {}&{\sqrt{y^{16}}}\\ {\text{Since} (y^8)^2=y^{16}}&{y^8}\\ \end{array}\]

    Example \(\PageIndex{17}\)

    Simplify:

    1. \(\sqrt{y^8}\)
    2. \(\sqrt{z^{12}}\).
    Answer
    1. \(y^4\)
    2. \(z^6\)

    Example \(\PageIndex{18}\)

    Simplify:

    1. \(\sqrt{m^4}\)
    2. \(\sqrt{b^{10}}\).
    Answer
    1. \(m^2\)
    2. \(b^5\)

    Example \(\PageIndex{19}\)

    Simplify: \(\sqrt{16n^2}\)

    Answer

    \[\begin{array}{ll} {}&{\sqrt{16n^2}}\\ {\text{Since} (4n)^2=16n^2}&{4n}\\ \end{array}\]

    Example \(\PageIndex{20}\)

    Simplify: \(\sqrt{64x^2}\).

    Answer

    \(8x\)

    Example \(\PageIndex{21}\)

    Simplify: \(\sqrt{169y^2}\).

    Answer

    \(13y\)

    Example \(\PageIndex{22}\)

    Simplify: \(−\sqrt{81c^2}\).

    Answer

    \[\begin{array}{ll} {}&{−\sqrt{81c^2}}\\ {\text{Since} (9c)^2=81c^2}&{−9c}\\ \end{array}\]

    Example \(\PageIndex{23}\)

    Simplify: \(−\sqrt{121y^2}\).

    Answer

    \(−11y\)

    Example \(\PageIndex{24}\)

    Simplify: \(−\sqrt{100p^2}\).

    Answer

    \(−10p\)

    Example \(\PageIndex{25}\)

    Simplify: \(\sqrt{36x^{2}y^{2}}\).

    Answer

    \[\begin{array}{ll} {}&{\sqrt{36x^{2}y^{2}}}\\ {\text{Since} (6xy)^2=\sqrt{36x^{2}y^{2}}}&{6xy}\\ \end{array}\]

    Example \(\PageIndex{26}\)

    Simplify: \(\sqrt{100a^{2}b^{2}}\).

    Answer

    10ab

    Example \(\PageIndex{27}\)

    Simplify: \(\sqrt{225m^{2}n^{2}}\).

    Answer

    15mn

    Example \(\PageIndex{28}\)

    Simplify: \(\sqrt{64p^{64}}\).

    Answer

    \[\begin{array}{ll} {}&{\sqrt{64p^{64}}}\\ {\text{Since} (8p^8)^2=\sqrt{64p^{64}}}&{8p^8}\\ \end{array}\]

    Example \(\PageIndex{29}\)

    Simplify: \(\sqrt{49x^{30}}\).

    Answer

    \(7x^{15}\)

    Example \(\PageIndex{30}\)

    Simplify: \(\sqrt{81w^{36}}\)

    Answer

    \(9w^{18}\)​​​​​​​

    Example \(\PageIndex{31}\)

    Simplify: \(\sqrt{121a^{6}b^{8}}\)

    Answer

    \[\begin{array}{ll} {}&{\sqrt{121a^{6}b^{8}}}\\ {\text{Since} (11a^{3}b^{4})^2=\sqrt{121a^{6}b^{8}}}&{11a^{3}b^{4}}\\ \end{array}\]

    Example \(\PageIndex{32}\)

    Simplify: \(\sqrt{169x^{10}y^{14}}\)

    Answer

    \(13x^{5}y^{7}\)

    Example \(\PageIndex{33}\)

    Simplify: \(\sqrt{144p^{12}q^{20}}\)

    Answer

    \(\sqrt{12p^{6}q^{10}}\)

    Access this online resource for additional instruction and practice with square roots.

    • Square Roots

    Key Concepts

    • Note that the square root of a negative number is not a real number.
    • Every positive number has two square roots, one positive and one negative. The positive square root of a positive number is the principal square root.
    • We can estimate square roots using nearby perfect squares.
    • We can approximate square roots using a calculator.
    • When we use the radical sign to take the square root of a variable expression, we should specify that \(x \ge 0\) to make sure we get the principal square root.

    Glossary

    square of a number
    • If \(n^2=m\), then m is the square of n
    square root of a number
    • If \(n^2=m\), then n is a square root of m
    square root notation
    • If \(m=n^2\), then \(\sqrt{m}=n\). We read \(\sqrt{m}\) as ‘the square root of m.’