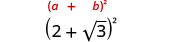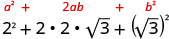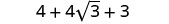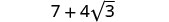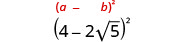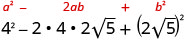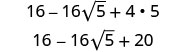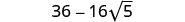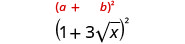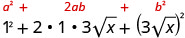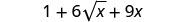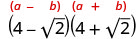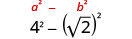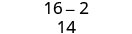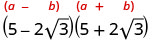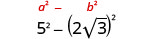Multiply Square Roots
We have used the Product Property of Square Roots to simplify square roots by removing the perfect square factors. The Product Property of Square Roots says
\[\sqrt{ab}=\sqrt{a}·\sqrt{b} \nonumber\]
We can use the Product Property of Square Roots ‘in reverse’ to multiply square roots.
\[\sqrt{a}·\sqrt{b}=\sqrt{ab} \nonumber\]
Remember, we assume all variables are greater than or equal to zero.
We will rewrite the Product Property of Square Roots so we see both ways together.
Definition: PRODUCT PROPERTY OF SQUARE ROOTS
If a, b are nonnegative real numbers, then
\(\sqrt{ab}=\sqrt{a}·\sqrt{b}\) and \(\sqrt{a}·\sqrt{b}=\sqrt{ab}\).
So we can multiply \(\sqrt{3}·\sqrt{5}\) in this way:
\[\begin{array}{l} {\sqrt{3}·\sqrt{5}}\\ {\sqrt{3·5}}\\ {\sqrt{15}}\\ \nonumber \end{array}\]
Sometimes the product gives us a perfect square:
\[\begin{array}{l} {\sqrt{2}·\sqrt{8}}\\ {\sqrt{2·8}}\\ {\sqrt{16}}\\ {4}\\ \nonumber \end{array}\]
Even when the product is not a perfect square, we must look for perfect-square factors and simplify the radical whenever possible.
Multiplying radicals with coefficients is much like multiplying variables with coefficients. To multiply 4x·3y we multiply the coefficients together and then the variables. The result is 12xy. Keep this in mind as you do these examples.
Example \(\PageIndex{1}\)
Simplify:
- \(\sqrt{2}·\sqrt{6}\)
- \((4\sqrt{3})(2\sqrt{12})\).
- Answer
-
| 1. |
\(\sqrt{2}·\sqrt{6}\) |
| Multiply using the Product Property. |
\(\sqrt{12}\) |
| Simplify the radical. |
\(\sqrt{4}·\sqrt{3}\) |
| Simplify. |
\(2\sqrt{3}\) |
| 2. |
\((4\sqrt{3})(2\sqrt{12})\) |
| Multiply using the Product Property. |
\(8\sqrt{36}\) |
| Simplify the radical. |
\(8·6\) |
| Simplify. |
\(48\) |
-
Example \(\PageIndex{2}\)
Simplify:
- \(\sqrt{3}·\sqrt{6}\)
- \((2\sqrt{6})(3\sqrt{12})\).
- Answer
-
- \(3\sqrt{2}\)
- \(36\sqrt{2}\)
Example \(\PageIndex{3}\)
Simplify:
- \(\sqrt{5}·\sqrt{10}\)
- \((6\sqrt{3})(5\sqrt{6})\)
- Answer
-
- \(5\sqrt{2}\)
- \(90\sqrt{2}\)
Example \(\PageIndex{4}\)
Simplify: \((6\sqrt{2})(3\sqrt{10})\)
- Answer
-
| |
\((6\sqrt{2})(3\sqrt{10})\) |
| Multiply using the Product Property. |
\(18\sqrt{20}\) |
| Simplify the radical. |
\(18\sqrt{4}·\sqrt{5}\) |
| Simplify. |
\(18·2·\sqrt{5}\) |
| |
\(36\sqrt{5}\) |
Example \(\PageIndex{5}\)
Simplify: \((3\sqrt{2})(2\sqrt{30})\)
- Answer
-
\(12\sqrt{15}\)
Example \(\PageIndex{6}\)
Simplify: \((3\sqrt{3})(3\sqrt{6})\).
- Answer
-
\(27\sqrt{2}\)
When we have to multiply square roots, we first find the product and then remove any perfect square factors.
Example \(\PageIndex{7}\)
Simplify:
- \((\sqrt{8x^3})(\sqrt{3x})\)
- \((\sqrt{20y^2})(\sqrt{5y^3})\)
- Answer
-
| 1. |
\((\sqrt{8x^3})(\sqrt{3x})\) |
| Multiply using the Product Property. |
\(\sqrt{24x^4}\) |
| Simplify the radical. |
\(\sqrt{4x^4}·\sqrt{6}\) |
| Simplify. |
\(2x^2\sqrt{6}\) |
| 2. |
\((\sqrt{20y^2})(\sqrt{5y^3})\) |
| Multiply using the Product Property. |
\(\sqrt{100y^5}\) |
| Simplify the radical. |
\(10y^2\sqrt{y}\) |
Example \(\PageIndex{8}\)
Simplify:
- \((\sqrt{6x^3})(\sqrt{3x})\)
- \((\sqrt{2y^3})(\sqrt{50y^2})\).
- Answer
-
- \(3x^2\sqrt{2}\)
- \(10y^2\sqrt{y}\)
Example \(\PageIndex{9}\)
Simplify:
- \((\sqrt{6x^5})(\sqrt{2x})\)
- \((\sqrt{12y^2})(\sqrt{3y^5})\)
- Answer
-
- \(2x^3\sqrt{3}\)
- \(6y^2\sqrt{y}\)
Example \(\PageIndex{10}\)
Simplify: \((10\sqrt{6p^3})(3\sqrt{18p})\)
- Answer
-
| |
\((10\sqrt{6p^3})(3\sqrt{18p})\) |
| Multiply. |
\(30\sqrt{108p^4}\) |
| Simplify the radical. |
\(30\sqrt{36p^4}·\sqrt{3}\) |
| |
\(30·6p^2·\sqrt{3}\) |
| |
\(180p^2\sqrt{3}\) |
Example \(\PageIndex{11}\)
Simplify: \((\sqrt{62x^2})(8\sqrt{45x^4})\)
- Answer
-
\(144x^3\sqrt{10}\)
Example \(\PageIndex{12}\)
Simplify: \((2\sqrt{6y^4})(12\sqrt{30y})\).
- Answer
-
\(144y^2\sqrt{5y}\)
Example \(\PageIndex{13}\)
Simplify:
- \((\sqrt{2})^2\)
- \((−\sqrt{11})^2\).
- Answer
-
| 1. |
\((\sqrt{2})^2\) |
| Rewrite as a product. |
\((\sqrt{2})(\sqrt{2})\) |
| Multiply. |
\(\sqrt{4}\) |
| Simplify. |
2 |
| 2. |
\((−\sqrt{11})^2\) |
| Rewrite as a product. |
\((−\sqrt{11})(−\sqrt{11})\) |
| Multiply. |
\(\sqrt{121}\) |
| Simplify. |
11 |
Example \(\PageIndex{14}\)
Simplify:
- \((\sqrt{12})^2\)
- \((−\sqrt{15})^2\).
- Answer
-
- 12
- 15
Example \(\PageIndex{15}\)
Simplify:
- \((\sqrt{16})^2\)
- \((−\sqrt{20})^2\).
- Answer
-
- 16
- 20
The results of the previous example lead us to this property.
Definition: SQUARING A SQUARE ROOT
If a is a nonnegative real number, then
\((\sqrt{a})^2=a\)
By realizing that squaring and taking a square root are ‘opposite’ operations, we can simplify \((\sqrt{2})^2\) and get 2 right away. When we multiply the two like square roots in part (a) of the next example, it is the same as squaring.
Example \(\PageIndex{16}\)
Simplify:
- \((2\sqrt{3})(8\sqrt{3})\)
- \((3\sqrt{6})^2\).
- Answer
-
| 1. |
\((2\sqrt{3})(8\sqrt{3})\) |
| Multiply. Remember, \((\sqrt{3}^2)\) |
16·3 |
| Simplify. |
48 |
| 2. |
\((3\sqrt{6})^2\) |
| Multiply. |
9·6 |
| Simplify. |
54 |
Example \(\PageIndex{17}\)
Simplify:
- \((6\sqrt{11})(5\sqrt{11})\)
- \((5\sqrt{8})^2\).
- Answer
-
- 330
- 200
Example \(\PageIndex{18}\)
Simplify:
- \((3\sqrt{7})(10\sqrt{7})\)
- \((−4\sqrt{6})^2\).
- Answer
-
- 210
- 96
Use Polynomial Multiplication to Multiply Square Roots
In the next few examples, we will use the Distributive Property to multiply expressions with square roots.
We will first distribute and then simplify the square roots when possible.
Example \(\PageIndex{19}\)
Simplify:
- \(3(5−\sqrt{2})\)
- \(\sqrt{2}(4−\sqrt{10})\).
- Answer
-
| 1. |
\(3(5−\sqrt{2})\) |
| Distribute. |
\(15−3\sqrt{2})\) |
| 2. |
\(\sqrt{2}(4−\sqrt{10})\) |
| Distribute. |
\(4\sqrt{2}−\sqrt{20}\) |
| Simplify. |
\(4\sqrt{2}−2\sqrt{5}\) |
Example \(\PageIndex{20}\)
Simplify:
- \(2(3−\sqrt{5})\)
- \(\sqrt{3}(2−\sqrt{18})\).
- Answer
-
- \(6−2\sqrt{5}\)
- \(2\sqrt{3}−3\sqrt{6}\)
Example \(\PageIndex{21}\)
Simplify:
- \(6(2+\sqrt{6})\)
- \(\sqrt{7}(1+\sqrt{14})\).
- Answer
-
- \(12+\sqrt{6}\)
- \(\sqrt{7}+7\sqrt{2}\)
Example \(\PageIndex{22}\)
Simplify:
- \(\sqrt{5}(7+2\sqrt{5})\)
- \(\sqrt{6}(\sqrt{2}+\sqrt{18})\).
- Answer
-
| 1. |
\(\sqrt{5}(7+2\sqrt{5})\) |
| Distribute. |
\(7\sqrt{5}+2·5\) |
| Simplify. |
\(7\sqrt{5}+10\) |
| |
\(10+7\sqrt{5}\) |
| 2. |
\(\sqrt{6}(\sqrt{2}+\sqrt{18})\) |
| Multiply. |
\(\sqrt{12}+\sqrt{108}\) |
| Simplify. |
\((\sqrt{4}·\sqrt{3}+\sqrt{36}·\sqrt{3})\) |
| |
\(2\sqrt{3}+6\sqrt{3}\) |
| Combine like radicals. |
\(8\sqrt{3}\) |
Example \(\PageIndex{23}\)
Simplify:
- \(\sqrt{6}(1+3\sqrt{6})\)
- \(\sqrt{12}(\sqrt{3}+\sqrt{24})\)
- Answer
-
- \(18+\sqrt{6}\)
- \(6+12\sqrt{2}\)
Example \(\PageIndex{24}\)
Simplify:
- \(\sqrt{8}(2−5\sqrt{8})\)
- \(\sqrt{14}(\sqrt{2}+\sqrt{42})\)
- Answer
-
- \(−40+4\sqrt{2}\)
- \(2\sqrt{7}+14\sqrt{3}\)
When we worked with polynomials, we multiplied binomials by binomials. Remember, this gave us four products before we combined any like terms. To be sure to get all four products, we organized our work—usually by the FOIL method.
Example \(\PageIndex{25}\)
Simplify: \((2+\sqrt{3})(4−\sqrt{3})\)
- Answer
-
| |
\((2+\sqrt{3})(4−\sqrt{3})\) |
| Multiply. |
\(8−2\sqrt{3}+4\sqrt{3}−3\) |
| Combine like terms. |
\(5+2\sqrt{3}\) |
Example \(\PageIndex{26}\)
Simplify: \((1+\sqrt{6})(3−\sqrt{6})\).
- Answer
-
\(−3+2\sqrt{6}\)
Example \(\PageIndex{27}\)
Simplify: \((4−\sqrt{10})(2+\sqrt{10})\).
- Answer
-
\(−2+2\sqrt{10}\)
Example \(\PageIndex{28}\)
Simplify: \((3−2\sqrt{7})(4−2\sqrt{7})\).
- Answer
-
| |
\((3−2\sqrt{7})(4−2\sqrt{7})\) |
| Multiply. |
\(12−6\sqrt{7}−8\sqrt{7}+4·7\) |
| Simplify. |
\(12−6\sqrt{7}−8\sqrt{7}+28\) |
| Combine like terms. |
\(40−14\sqrt{7}\) |
Example \(\PageIndex{29}\)
Simplify: \((6−3\sqrt{7})(3+4\sqrt{7})\).
- Answer
-
\(−66+15\sqrt{7}\)
Example \(\PageIndex{30}\)
Simplify: \((2−3\sqrt{11})(4−\sqrt{11})\)
- Answer
-
\(41+14\sqrt{11}\)
Example \(\PageIndex{31}\)
Simplify: \((3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\).
- Answer
-
| |
\(3\sqrt{2}−\sqrt{5})(\sqrt{2}+4\sqrt{5})\) |
| Multiply. |
\(3·2+12\sqrt{10}−\sqrt{10}−4·5\) |
| Simplify. |
\(6+12\sqrt{10}−\sqrt{10}−20\) |
| Combine like terms. |
\(−14+11\sqrt{10}\) |
Example \(\PageIndex{32}\)
Simplify: \((5\sqrt{3}−\sqrt{7})(\sqrt{3}+2\sqrt{7})\)
- Answer
-
\(1+9\sqrt{21}\)
Example \(\PageIndex{33}\)
Simplify: \((\sqrt{6}−3\sqrt{8})(2\sqrt{6}+\sqrt{8})\)
- Answer
-
\(−12−20\sqrt{3}\)
Example \(\PageIndex{34}\)
Simplify: \((4−2\sqrt{x})(1+3\sqrt{x})\).
- Answer
-
| |
\((4−2\sqrt{x})(1+3\sqrt{x})\). |
| Multiply. |
\(4+12\sqrt{x}−2\sqrt{x}−6x\) |
| Combine like terms. |
\(4+10\sqrt{x}−6x\) |
Example \(\PageIndex{35}\)
Simplify: \((6−5\sqrt{m})(2+3\sqrt{m})\).
- Answer
-
\(12+8\sqrt{m}−15m\)
Example \(\PageIndex{36}\)
Simplify: \((10+3\sqrt{n})(1−5\sqrt{n})\)
- Answer
-
\(10−47\sqrt{n}−15n\)
Note that some special products made our work easier when we multiplied binomials earlier. This is true when we multiply square roots, too. The special product formulas we used are shown below.
\[\begin{array}{ll} {\textbf{Binomial Squares}}&{\textbf{Product of Conjugates}}\\ {(a+b)^2=a^2+2ab+b^2}&{(a−b)(a+b)=a^2−b^2}\\ {(a−b)^2=a^2−2ab+b^2}&{}\\ \nonumber \end{array}\]
We will use the special product formulas in the next few examples. We will start with the Binomial Squares formula.
Example \(\PageIndex{38}\)
Simplify:
- \((10+\sqrt{2})^2\)
- \((1+3\sqrt{6})^2\).
- Answer
-
- \(102+20\sqrt{2}\)
- \(55+6\sqrt{6}\)
Exercise \(\PageIndex{39}\)
Simplify:
- \((6-\sqrt{5})^2\)
- \((9-2\sqrt{10})^2\).
- Answer
-
- \(41-12\sqrt{5}\)
- \(121-36\sqrt{10}\)
Example \(\PageIndex{41}\)
Simplify: \((2+5\sqrt{m})^2\).
- Answer
-
\(4+20\sqrt{m}+25m\)
Example \(\PageIndex{42}\)
Simplify: \((3−4\sqrt{n})^2\).
- Answer
-
\(9−24\sqrt{n}+16n\)
In the next two examples, we will find the product of conjugates.
Example \(\PageIndex{44}\)
Simplify: \((2−\sqrt{3})(2+\sqrt{3})\)
- Answer
-
1
ExAMPLe \(\PageIndex{45}\)
Simplify: \((1+\sqrt{5})(1−\sqrt{5})\)
- Answer
-
−4
Example \(\PageIndex{47}\)
Simplify: \((3−2\sqrt{5})(3+2\sqrt{5})\).
- Answer
-
−11
Example \(\PageIndex{48}\)
Simplify: \((4+5\sqrt{7})(4−5\sqrt{7})\).
- Answer
-
−159
Access these online resources for additional instruction and practice with multiplying square roots.
- Product Property
- Multiply Binomials with Square Roots