5.2: Identify and Evaluate Polynomials
- Page ID
- 51464
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Identify the terms, the coefficients, and the exponents of a polynomial
- Evaluate a polynomial for given values of the variable
- Simplify polynomials by collecting like terms
Identify the terms, the coefficients, and the exponents of a polynomial
Polynomials are algebraic expressions that are created by combining numbers and variables using arithmetic operations such as addition, subtraction, multiplication, division, and exponentiation. You can create a polynomial by adding or subtracting terms. Polynomials are very useful in applications from science and engineering to business. You may see a resemblance between expressions, which we have been studying in this course, and polynomials. Polynomials are a special sub-group of mathematical expressions and equations.
The following table is intended to help you tell the difference between what is a polynomial and what is not.
| IS a Polynomial | Is NOT a Polynomial | Because |
| \(\frac{2}{x^{2}}+x\) | Polynomials only have variables in the numerator | |
| \(\frac{2}{y}+4\) | Polynomials only have variables in the numerator | |
| \(\sqrt{a}+7\) | Variables under a root are not allowed in polynomials |
The basic building block of a polynomial is a monomial. A monomial is one term and can be a number, a variable, or the product of a number and variables with an exponent. The number part of the term is called the coefficient.
Examples of monomials:
- number: \({2}\)
- variable: \({x}\)
- product of number and variable: \({2x}\)
- product of number and variable with an exponent: \({2x}^{3}\)
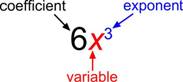
The coefficient can be any real number, including 0. The exponent of the variable must be a whole number—0, 1, 2, 3, and so on. A monomial cannot have a variable in the denominator or a negative exponent.
The value of the exponent is the degree of the monomial. Remember that a variable that appears to have no exponent really has an exponent of 1. And a monomial with no variable has a degree of 0. (Since \(x\neq0\), a number such as 3 could also be written \(x\neq0\) as \(3x^{0}=3\cdot1=3\).)
Example
Identify the coefficient, variable, and degree of the variable for the following monomial terms:
1) 9
2) x
3) \(\displaystyle \frac{3}{5}
Callstack:
at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/05:_Polynomials/5.02:_Identify_and_Evaluate_Polynomials), /content/body/div[2]/div[2]/p[1]/span, line 1, column 2
[reveal-answer q=”150661″]Show Solution[/reveal-answer]
[hidden-answer a=”150661″]
1)
9 is a constant so there is no coefficient or variable. Since there is no variable, we consider the degree to be 0.
2)
The variable is x.
The exponent of x is 1. \(x=x^{1}\), so the degree is 1.
The coefficient of x is 1. \(x=1x^{1}\).
3)
The variable is k.
The exponent of k is 8, so the degree is 8.
The coefficient of \(\displaystyle \frac{3}{5}\)
[/hidden-answer]
A polynomial is a monomial or the sum or difference of two or more polynomials. Each monomial is called a term of the polynomial.
Some polynomials have specific names indicated by their prefix.
- monomial—is a polynomial with exactly one term (“mono”—means one)
- binomial—is a polynomial with exactly two terms (“bi”—means two)
- trinomial—is a polynomial with exactly three terms (“tri”—means three)
The word “polynomial” has the prefix, “poly,” which means many. However, the word polynomial can be used for all numbers of terms, including only one term.
Because the exponent of the variable must be a whole number, monomials and polynomials cannot have a variable in the denominator.
Polynomials can be classified by the degree of the polynomial. The degree of a polynomial is the degree of its highest degree term. So the degree of \(2x^{3}+3x^{2}+8x+5\) is 3.
A polynomial is said to be written in standard form when the terms are arranged from the highest degree to the lowest degree. When it is written in standard form it is easy to determine the degree of the polynomial.
The table below illustrates some examples of monomials, binomials, trinomials, and other polynomials. They are all written in standard form.
| Monomials | Binomials | Trinomials | Other Polynomials | |||||
| 15 | \(x^{3}-x^{2}+1\) | \(\displaystyle \frac{1}{2}x\) | \(3x^{2}+2x-9\) | \(-4y^{3}\) | \(3y^{3}+y^{2}-2\) | \(16n^{4}\) | \(a^{7}+2a^{5}-3a^{3}\) | \(q^{7}+2q^{5}-3q^{3}+q\) |
When the coefficient of a polynomial term is 0, you usually do not write the term at all (because 0 times anything is 0, and adding 0 doesn’t change the value). The last binomial above could be written as a trinomial, \(14y^{3}+0y^{2}+3y\).
A term without a variable is called a constant term, and the degree of that term is 0. For example 13 is the constant term in \(14y^{3}+3y\) has no constant term or that the constant term is 0.
Example
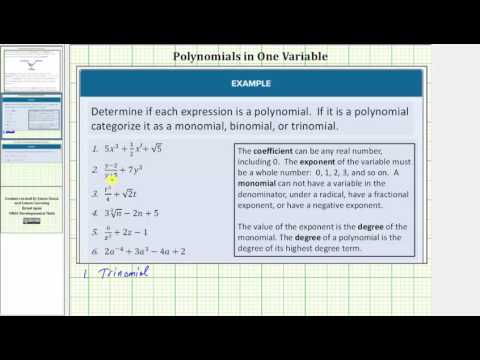
For the following expressions, determine whether they are a polynomial. If so, categorize them as a monomial, binomial, or trinomial.
- \(\frac{x-3}{1-x}+x^2\)
- \(t^2+2t-3\)
- \(x^3+\frac{x}{8}\)
- \(\frac{\sqrt{y}}{2}-y-1\)
[reveal-answer q=”239104″]Show Solution[/reveal-answer]
[hidden-answer a=”239104″]
- \(\frac{x-3}{1-x}+x^2\) is not a polynomial because it violates the rule that polynomials cannot have variables in the denominator of a fraction.
- \(t^2+2t-3\) is a polynomial because it is an expression whose terms are connected by addition and subtraction, and there are no variables under a root or in the denominator of a fraction. There are three terms in this polynomial so it is a trinomial.
- \(x^3+\frac{x}{8}\)is a polynomial because it is an expression whose terms are connected by addition and subtraction, and there are no variables under a root or in the denominator of a fraction. There are two terms in this polynomial so it is a binomial.
- \(\frac{\sqrt{y}}{2}-y-1\) is not a polynomial because it violates the rule that polynomials cannot have variables under a root.
[/hidden-answer]
In the following video, you will be shown more examples of how to identify and categorize polynomials.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=102
Evaluate a polynomial for given values of the variable
You can evaluate polynomials just as you have been evaluating expressions all along. To evaluate an expression for a value of the variable, you substitute the value for the variable every time it appears. Then use the order of operations to find the resulting value for the expression.
Example
Evaluate \(x=-1\).
[reveal-answer q=”280466″]Show Solution[/reveal-answer]
[hidden-answer a=”280466″]Substitute \(-1\) for each x in the polynomial.
\(3\left(-1\right)^{2}-2\left(-1\right)+1\)
Following the order of operations, evaluate exponents first.
\(3\left(1\right)-2\left(-1\right)+1\)
Multiply 3 times 1, and then multiply \(-1\).
\(3+\left(-2\right)\left(-1\right)+1\)
Change the subtraction to addition of the opposite.
\(3+2+1\)
Find the sum.
Answer
\(x=-1\)
[/hidden-answer]
Example
Evaluate \(p = 3\).
[reveal-answer q=”745542″]Show Solution[/reveal-answer]
[hidden-answer a=”745542″]Substitute 3 for each p in the polynomial.
\(\displaystyle -\frac{2}{3}\left(3\right)^{4}+2\left(3\right)^{3}-3\)
Following the order of operations, evaluate exponents first and then multiply.
\(\displaystyle -\frac{2}{3}\left(81\right)+2\left(27\right)-3\)
Add and then subtract to get \(-3\).
\(-54 + 54 – 3\)
Answer
\(p = 3\)
[/hidden-answer]
The following video presents more examples of evaluating a polynomial for a given value.
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=102
Simplify polynomials by collecting like terms
A polynomial may need to be simplified. One way to simplify a polynomial is to combine the like terms if there are any. Two or more terms in a polynomial are like terms if they have the same variable (or variables) with the same exponent. For example, \(-5x^{2}\) are like terms: They both have x as the variable, and the exponent is 2 for each. However, \(3x\) are not like terms, because their exponents are different.
Here are some examples of terms that are alike and some that are unlike.
| Term | Like Terms | UNLike Terms |
| \(3a, \,\,\,-2a,\,\,\, \frac{1}{2}a\) | \(a^2\) | \(\frac{1}{a^2},\,\,\,\sqrt{a^2},\,\,\, a^3\) |
| \(7ab,\,\,\,0.23ab,\,\,\,\frac{2}{3}ab,\,\,\,-ab\) | \(ab^2\) | \(a^2b,\,\,\, ab,\,\,\,\sqrt{ab^2},\,\,\,\frac{1}{ab^2}\) |
Example
Which of these terms are like terms?
\(7x^{3}7x7y-8x^{3}9y-3x^{2}8y^{2}\)
[reveal-answer q=”413363″]Show Solution[/reveal-answer]
[hidden-answer a=”413363″]Like terms must have the same variables, so first identify which terms use the same variables.
\(\begin{array}{l}x:7x^{3}7x-8x^{3}-3x^{2}\\y:7y9y8y^{2}\end{array}\)
Like terms must also have the same exponents. Identify which terms with the same variables also use the same exponents.
The x terms \(-8x^{3}\) have the same exponent.
The y terms \(9y\) have the same exponent.
Answer
\(-8x^{3}\) are like terms.
\(9y\) are like terms.
[/hidden-answer]
You can use the distributive property to simplify the sum of like terms. Recall that the distributive property of addition states that the product of a number and a sum (or difference) is equal to the sum (or difference) of the products.
\(2\left(3+6\right)=2\left(3\right)+2\left(6\right)\)
Both expressions equal 18. So you can write the expression in whichever form is the most useful.
Let’s see how we can use this property to combine like terms.
Example
Simplify \(3x^{2}-5x^{2}\).
[reveal-answer q=”969840″]Show Solution[/reveal-answer]
[hidden-answer a=”969840″]\(5x^{2}\) are like terms.
\(3\left(x^{2}\right)-5\left(x^{2}\right)\)
We can rewrite the expression as the product of the difference.
\(\left(3-5\right)\left(x^{2}\right)\)
Calculate \(3–5\).
\(\left(-2\right)\left(x^{2}\right)\)
Write the difference of \(3 – 5\) as the new coefficient.
Answer
\(3x^{2}-5x^{2}=-2x^{2}\)
[/hidden-answer]
You may have noticed that combining like terms involves combining the coefficients to find the new coefficient of the like term. You can use this as a shortcut.
Example
Simplify \(6a^{4}+4a^{4}\).
[reveal-answer q=”840415″]Show Solution[/reveal-answer]
[hidden-answer a=”840415″]Notice that both terms have a number multiplied by \(a^{4}\). This makes them like terms.
\(6a^{4}+4a^{4}\)
Combine the coefficients, 6 and 4.
\(\left(6+4\right)\left(a^{4}\right)\)
Calculate the sum.
\(\left(10\right)\left(a^{4}\right)\)
Write the sum as the new coefficient.
Answer
\(6a^{4}+4a^{4}=10a^{4}\)
[/hidden-answer]
When you have a polynomial with more terms, you have to be careful that you combine only like terms. If two terms are not like terms, you can’t combine them.
Example
Simplify \(3x^{2}+3x+x+1+5x\)
[reveal-answer q=”731804″]Show Solution[/reveal-answer]
[hidden-answer a=”731804″]First identify which terms are like terms: only \(x\), and \(5x\) are like terms.
\(x\), and \(5x\) are like terms.
Use the commutative and associative properties to group the like terms together.
\(\begin{array}{l}3x^{2}+3x+x+1+5x\\3x^{2}+\left(3x+x+5x\right)+1\end{array}\)
Add the coefficients of the like terms. Remember that the coefficient of x is \(1\left(x=1x\right)\).
\(\begin{array}{l}3x^{2}+\left(3+1+5\right)x+1\\3x^{2}+\left(9\right)x+1\end{array}\)
Write the sum as the new coefficient.
Answer
\(3x^{2}+3x+x+1+5x=3x^{2}+9x+1\)
[/hidden-answer]
A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=102
Summary
Polynomials are algebraic expressions that contain any number of terms combined by using addition or subtraction. A term is a number, a variable, or a product of a number and one or more variables with exponents. Like terms (same variable or variables raised to the same power) can be combined to simplify a polynomial. The polynomials can be evaluated by substituting a given value of the variable into each instance of the variable, then using order of operations to complete the calculations.
- Determine if an Expression is a Polynomial. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/nPAqfuoSbPI. License: CC BY: Attribution
- Evaluate a Polynomial in One Variable. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/2EeFrgQP1hM. License: CC BY: Attribution
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Identify Like Terms and Combine Like. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/1epjbVO_qU4. License: CC BY: Attribution
- Unit 11: Exponents and Polynomials, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
- Apple and Orange - they do not compare. Authored by: By Michael Johnson . Located at: https://commons.wikimedia.org/wiki/File%3AApple_and_Orange_-_they_do_not_compare.jpg. License: CC BY: Attribution