4.5: Index Sets and Partitions

\[\bigcup_{i=1}^n A_i \mbox{  and  } \bigcap_{i=1}^n A_i\]

The notion of union can be extended to three sets: \[A\cup B\cup C = \{x\in{\cal U} \mid (x\in A) \vee (x\in B) \vee (x\in C) \}.\] It is obvious how to generalize it to the union of any number of sets. We use a notation that resembles the summation notation to describe such a union: \[\bigcup_{i=1}^n A_i = A_1 \cup A_2 \cup \cdots \cup A_n.\] We define

\[\bigcup_{i=1}^n A_i = \{x\in{\cal U} \mid (x\in A_1) \vee (x\in A_2) \vee\cdots\vee (x\in A_n)\}.\] It looks messy! Here is a better alternative:

\[\bigcup_{i=1}^n A_i =\{x\in{\cal U} \mid x\in A_i \mbox{ for } some \, \, i \in \mathbb{N},  \mbox{ where } 1\leq i \leq n\}.\]

In a similar manner, \(\displaystyle \bigcap_{i=1}^n A_i = A_1 \cap A_2 \cap \cdots \cap A_n\), and we define

\[\bigcap_{i=1}^n A_i
= \{x\in{\cal U} \mid x\in A_i \mbox{ for } all \, \, i \in \mathbb{N},
\mbox{ where } 1\leq i\leq n\}\]

In plain English, \(\displaystyle\bigcup_{i=1}^n A_i\) is the collection of all elements in the \(A_i\)’s, and \(\displaystyle\bigcap_{i=1}^n A_n\) is the collection of all elements common to all \(A_i\)’s.

Example \(\PageIndex{1}\label{eg:indexset-01}\)

For \(i=1,2,3,\ldots\,\), let \(A_i = [-i,i]\). First, construct several \(A_i\) for comparison, because it may help us detect any specific pattern. See Figure below.  It is clear that \(A_1 \subset A_2 \subset \cdots\,\). Thus, \(\displaystyle\bigcup_{i=1}^n A_i = [-n,n] = A_n\), and \(\displaystyle\bigcap_{i=1}^n A_i = [-1,1] = A_1\).

hands-on Exercise \(\PageIndex{1}\label{he:indexset-01}\)

Evaluate \(\displaystyle\bigcup_{i=1}^n B_i\) and \(\displaystyle\bigcap_{i=1}^n B_i\), where \(B_i = [0,2i) \text{ for } i \in \mathbb{N}\).

\[\bigcup_{i=1}^\infty A_i \mbox{  and  } \bigcap_{i=1}^\infty A_i\]

It is obvious that we can also extend the upper bound to infinity. \[\begin{aligned} \bigcup_{i=1}^\infty A_i &=& A_1 \cup A_2 \cup \cdots = \{ x\in{\cal U} \mid x\in A_i \mbox{ for }some \, \,  i \in \mathbb{N} \}, \\ \bigcap_{i=1}^\infty A_i &=& A_1 \cap A_2 \cap \cdots = \{ x\in{\cal U} \mid x\in A_i \mbox{ for } all \, \,  i \in \mathbb{N} \}. \end{aligned}\] In some situations, we may borrow the idea of partial sums from calculus. We first find the union or intersection of the first \(n\) sets, then take the limit as \(n\) approaches infinity. Thus, if the limit is well-defined, the

\[\bigcup_{i=1}^\infty A_i = \lim_{n\to\infty} \bigcup_{i=1}^n A_i, \qquad\mbox{and}\qquad \bigcap_{i=1}^\infty A_i = \lim_{n\to\infty} \bigcap_{i=1}^n A_i.\]

Example \(\PageIndex{2}\label{eg:indexset-02}\)

Let \(A_i = [-i,i]\). We have learned from the last example that \(\displaystyle\bigcup_{i=1}^n A_i = [-n,n]\) and \(\displaystyle\bigcap_{i=1}^n A_i = [-1,1]\). Hence, \[\bigcup_{i=1}^\infty A_i = \lim_{n\to\infty} [-n,n] = (-\infty,\infty), \qquad\mbox{and}\qquad \bigcap_{i=1}^\infty A_i = [-1,1].\] Recall that we write \((-\infty,\infty)\) instead of \([-\infty,\infty]\) because \(\pm\infty\) are not numbers, they are merely symbols representing infinitely large values.

hands-on Exercise \(\PageIndex{2}\label{he:indexset-02}\)

Evaluate \(\displaystyle\bigcup_{i=1}^\infty B_i\) and \(\displaystyle\bigcap_{i=1}^\infty B_i\), where \(B_i = [0,2i)\).

Example \(\PageIndex{3}\label{eg:indexset-03}\)

Let \(B_i = \left(0,1-\frac{1}{2i}\right]\). Determine \(\displaystyle\bigcup_{i=1}^\infty B_i\) and \(\displaystyle\bigcap_{i=1}^\infty B_i\).

Solution

Once again, we have \(B_1 \subset B_2 \subset \cdots\,\). It is easy to check that \[\bigcup_{i=1}^n B_i = B_n = \left(0,1-\frac{1}{2n}\right], \qquad\mbox{and}\qquad \bigcap_{i=1}^n B_i = B_1 = \left(0,\frac{1}{2}\right].\] It follows that \[\bigcup_{i=1}^\infty B_i = \lim_{n\to\infty} \left(0,1-\frac{1}{2n}\right] = (0,1), \qquad\mbox{and}\qquad \bigcap_{i=1}^\infty B_i = \left(0,\frac{1}{2}\right].\] Note that \(\lim_{n\to\infty} \left(0,1-\frac{1}{2n}\right] \neq (0,1]\) because the endpoint 1 does not belong to any \(B_i\).

hands-on Exercise \(\PageIndex{3}\label{he:indexset-03}\)

Let \(C_i = \left[0,1-\frac{1}{i}\right]\). Determine \(\displaystyle\bigcup_{i=1}^\infty C_i\) and \( \displaystyle\bigcap_{i=1}^\infty C_i\).

Example \(\PageIndex{4}\label{eg:indexset-04}\)

Let \(D_i = \left(1-\frac{1}{i},1+\frac{1}{i}\right)\). Determine \(\displaystyle\bigcup_{i=1}^\infty D_i\) and \(\displaystyle\bigcap_{i=1}^\infty D_i\).

Solution

As the value of \(i\) increases, the value of \(\frac{1}{i}\) decreases. Hence, the left endpoint \(1-\frac{1}{i}\) increases, and the right endpoint \(1+\frac{1}{i}\) decreases.

\(\begin{array}{|c|c|} \hline i & D_i = \big(1-\frac{1}{i},1+\frac{1}{i}\big) \\ \hline 1 & (0,2) \\ [6pt] 2 & \big(\frac{1}{2},\frac{3}{2}\big) \\ [6pt] 3 & \big(\frac{2}{3},\frac{4}{3}\big) \\ [6pt] 4 & \big(\frac{3}{4},\frac{5}{4}\big) \\ \hline \end{array}\)

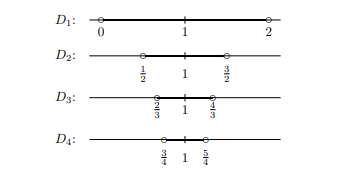
It is clear that \(D_1\supseteq D_2 \supseteq D_3 \supseteq \cdots\,\). Thus, \(\displaystyle\bigcup_{i=1}^\infty D_i = D_1 = (0,2)\), and \(\displaystyle\bigcap_{i=1}^\infty D_i = \{1\}\).

hands-on exercise \(\PageIndex{4}\label{he:indexset-04}\)

Let \(E_i = \left[-i,1+\frac{1}{i}\right)\). Determine \(\displaystyle\bigcup_{i=1}^\infty E_i\) and \(\displaystyle\bigcap_{i=1}^\infty E_i\).

hands-on Exercise \(\PageIndex{5}\label{he:indexset-05}\)

For each positive integer \(i\), define \(F_i=\{i,i+1,i+2,\ldots,3i\}\). Determine \(\displaystyle\bigcup_{i=1}^\infty F_i\) and \(\displaystyle\bigcap_{i=1}^\infty F_i\).

The next two results are obvious.

Theorem \(\PageIndex{1}\label{subsetcap}\)

If \(A_1 \subseteq A_2 \subseteq A_3 \subseteq \cdots\,\), then \(\displaystyle\bigcap_{i=1}^\infty A_i = A_1\).

Theorem \(\PageIndex{2}\)

If \(A_1 \supseteq A_2 \supseteq A_3 \supseteq \cdots\), then \(\displaystyle\bigcup_{i=1}^\infty A_i = A_1\).

Indexed Family of Sets

How could we describe the union \(A_2 \cup A_4 \cup A_6 \cup \cdots\,\)? Well, we can write \[\bigcup_{i \small \, even} A_i,\] which means that union of \(A_i\), where \(i\) is even. Since the set of even positive integers is denoted by \(2\mathbb{N}\), another way to describe the same union is \[\bigcup_{i\in2\mathbb{N}} A_i.\] It means the union all \(A_i\), where \(i\) is taken out from the set \(2\mathbb{N}\). Accordingly, \[\bigcup_{i=0}^\infty A_i = \bigcup_{i\in\mathbb{N}} A_i, \qquad\mbox{and}\qquad \bigcap_{i=0}^\infty A_i = \bigcap_{i\in\mathbb{N}} A_i.\] We can even go one step further, by allowing \(i\) to be taken from any set of integers, or any set of real numbers, or even any set of objects. The only restriction is that \(A_i\) must exist, and its content must somehow depend on \(i\).

In general, given a nonempty set \(I\), if we could associate with each \(i\in I\) a set \(A_i\), we define the indexed family of sets \({\cal A}\) as \[{\cal A} = \{ A_i \mid i\in I \}.\] We call \(I\) the index set, and define \[\begin{aligned} \bigcup_{i\in I} A_i &=& \{ x \mid x\in A_i \mbox{ for }some \, \,  i\in I \}, \\ \bigcap_{i\in I} A_i &=& \{ x \mid x\in A_i \mbox{ for } all \, \,  i\in I \}. \end{aligned}\] Let us look at a few examples.

Example \(\PageIndex{5}\label{eg:indexset-05}\)

To describe the union \[A_1\cup A_3\cup A_7\cup A_{11}\cup A_{23},\] we first define the index set to be \(I=\{1,3,7,11,23\}\), which is the set of all the subscripts used in the union. Now the union can be conveniently described as \(\displaystyle\bigcup_{i\in I} A_i\).

Example \(\PageIndex{6}\label{eg:indexset-06}\)

Consider five sets \[\begin{aligned} A_1 &=& \{1,4,23\}, \\ A_2 &=& \{7,11,23\}, \\ A_3 &=& \{3,6,9\}, \\ A_4 &=& \{5,17,22\}, \\ A_5 &=& \{3,6,23\}. \end{aligned}\] Let \(I=\{2,5\}\), then \[\bigcup_{i\in I} A_i = A_2 \cup A_5 = \{7,11,23\} \cup \{3,6,23\} = \{3,6,7,11,23\}.\] Likewise, \(\displaystyle\bigcap_{i\in I} A_i = A_2 \cap A_5 = \{7,11,23\} \cap \{3,6,23\} = \{23\}\).

hands-on Exercise \(\PageIndex{6}\label{he:indexset-06}\)

Let \(J=\{1,4,5\}\). Evaluate \(\displaystyle\bigcup_{i\in J} A_i\) and \(\displaystyle\bigcap_{i\in J} A_i\), where \(A_i\)s are defined in the last example.

hands-on Exercise \(\PageIndex{7}\label{he:indexset-07}\)

An index set could be a set of any objects. For instance, the sets of numbers in the last example could be the favorite Lotto numbers of five different students. We could index these sets according to the names of the students: \[\begin{aligned} A_{\small John} &=& \{1,4,23\}, \\ A_{\small Mary} &=& \{7,11,23\}, \\ A_{\small Joe} &=& \{3,6,9\}, \\ A_{\small Pete} &=& \{5,17,22\}, \\ A_{\small Lucy} &=& \{3,6,23\}. \end{aligned}\] If \(I=\{\mbox{Mary},\mbox{Joe},\mbox{Lucy}\}\), what is \(\bigcup_{i\in I}\)? How would you interpret its physical meaning?

example \(\PageIndex{7}\label{eg:indexset-07}\)

Let \(I = \{x\mid x \mbox{ is a living human being} \,\}\), and define \[\begin{aligned} B_i &=& \{ x \in I \mid x \mbox{ is a child of } i \}, \\ A_i &=& \{ i \} \cup B_i \end{aligned}\] for each \(i\in I\). Then \[\bigcap_{i\in I} A_i = \emptyset, \qquad \bigcup_{i\in I} A_i = I, \qquad \bigcap_{i\in I} B_i = \emptyset,\] and \[\bigcup_{i\in I} B_i = I - \{ x \mid x\mbox{'s parents are both deceased}\,\}.\] We leave it as an exercise to verify these unions and intersections.

hands-on Exercise \(\PageIndex{8}\label{he:indexset-08}\)

Verify the intersection and union in the last example.

hands-onExercise \(\PageIndex{9}\label{he:indexset-09}\)

If \(I\) represents a set of students, and \(A_i\) represents the set of friends of student \(i\), interpret the meaning of \(\displaystyle \bigcup_{i\in I} A_i\) and \(\bigcap_{i\in I} A_i\).

We close this section with yet another generalization of De Morgan’s laws.

Theorem \(\PageIndex{3}\) Extended De Morgan's laws

For any nonempty index set \(I\), we have \[\overline{\bigcup_{i\in I} A_i} = \bigcap_{i\in I} \overline{A_i}, \qquad\mbox{ and }\qquad \overline{\bigcap_{i\in I} A_i} = \bigcup_{i\in I} \overline{A_i}.\]

Proof 1

Let \(x\in \overline{\displaystyle\bigcup_{i\in I} A_i}\), then \[x\notin \bigcup_{i\in I} A_i = \{ x \mid x\in A_i \mbox{ for } some \,\,  i\in I \}.\] This means \(x\notin A_i\) for every \(i\in I\). Hence, \(x\in \overline{A_i}\) for each \(i\in I\). Consequently, \[x\in \bigcap_{i\in I} \overline{A_i}.\] This proves that \(\overline{\displaystyle\bigcup_{i\in I} A_i} \subseteq \bigcap_{i\in I} \overline{A_i}\).

Next, let \(x\in \displaystyle\bigcap_{i\in I} \overline{A_i}\). Then \(x\in \overline{A_i}\) for each \(i\in I\). This means \(x\notin A_i\) for each \(i\in I\). Then \[x\notin \{ x \mid x\in A_i \mbox{ for }some \,\,  i\in I \} = \bigcup_{i\in I} A_i.\] Thus, \(x\in \overline{\displaystyle\bigcup_{i\in I} A_i}\), proving that \(\displaystyle\bigcap_{i\in I} \overline{A_i} \subseteq \overline{\displaystyle\bigcup_{i\in I} A_i}\). We proved earlier that \(\overline{\displaystyle\bigcup_{i\in I} A_i} \subseteq \displaystyle\bigcap_{i\in I} \overline{A_i}\). Therefore, the two sets must be equal.
The proof of \(\overline{\displaystyle\bigcap_{i\in I} A_i} =\displaystyle \bigcup_{i\in I} \overline{A_i}\) proceeds in a similar manner, and is left as an exercise.

 

Proof 2

We shall prove \(\overline{\displaystyle\bigcup_{i\in I} A_i} = \displaystyle\bigcap_{i\in I} \overline{A_i}\). We leave out the explanations for you to fill in: \[\begin{aligned} x\in \overline{\bigcup_{i\in I} A_i} &\Leftrightarrow& \overline{x\in \bigcup_{i\in I} A_i} \\ &\Leftrightarrow& \overline{x\in A_i \mbox{ for some $i$}} \\ &\Leftrightarrow& x\notin A_i \mbox{ for all $i$} \\ &\Leftrightarrow& x\in \overline{A_i} \mbox{ for all $i$} \\ &\Leftrightarrow& x\in \bigcap_{i\in I} \overline{A_i}. \end{aligned}\] The proof of \(\overline{\displaystyle\bigcap_{i\in I} A_i} = \displaystyle\bigcup_{i\in I} \overline{A_i}\) is left as an exercise.

Partitions of Sets

Definition: Mutually Disjoint

Sets \(A_1, A_2, A_3, \ldots \) are mutually disjoint (or pairwise disjoint) if and only if no two sets with distinct subscripts have any elements in common.

Specifically, for all \(j=1,2,3, \ldots\)

\[A_i \cap A_j=\emptyset\mbox{   whenever    } i \neq j.\]

Definition: Partition

A finite or infinite collection of non-empty sets  \(\{A_1, A_2, A_3, \ldots\}\) is a partition of set \(A\) if and only if

(1) \(A\) is the union of all the \(A_i.\)

(2) The sets \(\{A_1, A_2, A_3, \ldots\}\) are mutually disjoint.

Example \(\PageIndex{8}\)

Let \(S=\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}.\)  Which of the following collections of sets are a partition of set \(S\)?

(a) \(A=\{A_1,A_2\}\)  with    \(A_1=\{1,3,5,7,9\}, A_2=\{2,4,6,8,10\}\)

(b) \(B=\{B_1,B_2,B_3\}\)  with  \(B_1=\{1,2,3,4,5,6,9\}, B_2=\{7\}, B_3=\{8,9,10\}\)

(c) \(C=\{C_1,C_2,C_3,C_4\}\)  with   \(C_1=\{8,10\}, C_2=\{3\},C_3=\{1,4,9\},C_4=\{2,5,6,7\}, \)

(d) \(D=\{D_1,D_2,D_3,D_4\}\)  with   \(D_1=\{1\}, D_2=\{2\},D_3=\{3\}, D_4=\{4\},D_5=\{5,6,7,8,9,10\}, \)

(e) \(E=\{E_1,E_2\}\)  with   \(E_1=\{1,3,5,7,9\}, E_2=\{0,2,4,6,8,10\}\)

(f) \(F=\{F_1,F_2,F_3\}\)  with   \(F_1=\{1,2,3,4\}, F_2=\{5,6,7\}, F_3=\{9,10\}\)

Solution

(a), (c) & (d)

Summary and Review

• When dealing with arbitrary intersection or union of intervals, first identify the endpoints, then analyze the sets involved in the operation to determine whether an endpoint should be included or excluded.
• Intersection and union can be performed on a group of similar sets identified by subscripts belonging to an index set.
• Consequently, intersection or union can be formed by naming a specific index set.
• A collection of sets can be a partition of a set if it satisfies two conditions.

Exercises 

Exercise \(\PageIndex{1}\label{ex:indexset-01}\)

For each \(n\in\mathbb{Z}^+\), define \(A_n=\left(-\frac{1}{n},2n\right)\). Find \(\displaystyle{\bigcap_{n=1}^\infty} A_n\) and \(\displaystyle{\bigcup_{n=1}^\infty} A_n\).
 

Answer

\(\displaystyle{\bigcap_{n=1}^\infty} A_n = (0,2)\), \(\displaystyle{\bigcup_{n=1}^\infty} A_n = (-1,\infty)\).

Exercise \(\PageIndex{2}\label{ex:indexset-02}\)

For each \(n\in\mathbb{Z}^+\), define \(B_n = \{m\in\mathbb{Z} \mid -\frac{n}{2}\leq m\leq 3n\}\). Evaluate \(\displaystyle{\bigcap_{n=1}^\infty} B_n\) and \(\displaystyle{\bigcup_{n=1}^\infty} B_n\).

Exercise \(\PageIndex{3}\label{ex:indexset-03}\)

Define \(C_n=\{n,n+1,n+2,\ldots,2n+1\}\) for each integer \(n\geq0\). Evaluate \(\displaystyle{\bigcap_{n=0}^\infty} C_n\) and \(\displaystyle{\bigcup_{n=0}^\infty} C_n\).
 

Answer

\(\displaystyle{\bigcap_{n=0}^\infty} C_n = \emptyset\), \(\displaystyle{\bigcup_{n=0}^\infty} C_n = \mathbb{N}\cup\{0\}\).

Exercise \(\PageIndex{4}\label{ex:indexset-04}\)

For each \(n\in I = \{1,2,3,\ldots,100\}\), define \(D_n=[-n,2n]\cap\mathbb{Z}\). Evaluate \(\displaystyle{\bigcap_{n\in I}} D_n\) and \(\displaystyle{\bigcup_{n\in I}} D_n\).

Exercise \(\PageIndex{5}\label{ex:indexset-05}\)

For each \(n\in\mathbb{N}\), define \(E_n = \{-n,-n+1,-n+2,\ldots,n^2\}\). Evaluate \(\displaystyle{\bigcap_{n\in\mathbb{N}}} E_n\) and \(\displaystyle{\bigcup_{n\in\mathbb{N}}} E_n\).
 

Answer

\(\displaystyle{\bigcap_{n\in\mathbb{N}}} E_n = E_1 = \{-1,0,1\}\), \(\displaystyle{\bigcup_{n\in\mathbb{N}}} E_n = \mathbb{Z}\).

Exercise \(\PageIndex{6}\label{ex:indexset-06}\)

For each \(n\in\mathbb{N}\), define \(F_n = \left\{\frac{m}{n} \mid m\in\mathbb{Z}\right\}\). Evaluate \(\displaystyle{\bigcap_{n\in\mathbb{N}}} F_n\) and \(\displaystyle{\bigcup_{n\in\mathbb{N}}} F_n\).

Exercise \(\PageIndex{7}\label{ex:indexset-07}\)

Let \(I=(0,1)\), and define \(A_i = \left[1,\frac{1}{i}\right]\) for each \(i\in I\). For instance \(A_{0.5} = [1,2]\) and \(A_{\frac{\pi}{4}} = \left[1,\frac{4}{\pi}\right]\). Evaluate \(\displaystyle{\bigcup_{i\in I}} A_i\) and \(\displaystyle{\bigcap_{i\in I}} A_i\).
 

Answer

\(\displaystyle{\bigcup_{i\in I}} A_i = [1,\infty)\), \(\displaystyle{\bigcap_{i\in I}} A_i = \{1\}\).

Exercise \(\PageIndex{8}\label{ex:indexset-08}\)

Define \(I=(0,1)\), and for each \(i\in I\), let \(B_i=(-i,\frac{1}{i})\). Evaluate \(\displaystyle{\bigcup_{i\in I}} B_i = (-1,\infty)\) and \(\displaystyle{\bigcap_{i\in I} }B_i\).

Exercise \(\PageIndex{9}\label{ex:indexset-09}\)

Evaluate \(\displaystyle{\bigcap_{x\in(1,2)}}(1-2x,x^2)\) and \(\displaystyle{\bigcup_{x\in(1,2)}} (1-2x,x^2)\).
 

Answer

\(\displaystyle{\bigcap_{x\in(1,2)}} (1-2x,x^2) = [-1,1]\), \(\displaystyle{\bigcup_{x\in(1,2)}} (1-2x,x^2) = (-3.4)\).

Exercise \(\PageIndex{10}\label{ex:indexset-10}\)

Evaluate \(\displaystyle{\bigcap_{x\in(0,1)}} \left(x,\frac{1}{x}\right)\) and \(\displaystyle{\bigcup_{x\in(0,1)}} \left(x,\frac{1}{x}\right)\).

Exercise \(\PageIndex{11}\label{ex:indexset-11}\)

Let the universal set be \(\mathbb{R}^2\). For each \(r\in(0,\infty)\), define \[A_r = \{(x,y)\mid y=rx^2\};\] that is, \(A_r\) is the set of points on the parabola \(y=rx^2\), where \(r>0\). Evaluate \(\displaystyle{\bigcap_{r\in(0,\infty)}} A_r\) and \(\displaystyle{\bigcup_{r\in(0,\infty)}} A_r\).
 

Answer

\(\displaystyle{\bigcap_{r\in(0,\infty)}} A_r = \{(0,0)\}\), \(\displaystyle{\bigcup_{r\in(0,\infty)}} A_r = \mathbb{R}^*\times\mathbb{R}^+ \cup \{(0,0)\}\).

Exercise \(\PageIndex{12}\label{ex:indexset-12}\)

Prove that \(\displaystyle{ \overline{\bigcap_{i\in I} A_i}} = \displaystyle{\bigcup_{i\in I}} \overline{A_i}\) for any nonempty index set \(I\).

Exercise \(\PageIndex{13}\)

Let \(A_i = [-\frac{1}{i},5i]\) for \(i \in \mathbb{Z}^+.\)
Find:
(a) \(A_1= \quad    (b)\, A_3=  \quad   (c)\, A_6=\)

Answer

(a) \(A_1=[-1,5]\quad (b)\, A_3=[-\frac{1}{3},15]\quad \quad\quad  (c)\, A_6=[-\frac{1}{6},30]\)

Exercise \(\PageIndex{14}\)

Let \(A_i = [-\frac{1}{i},5i]\) for \(i \in \mathbb{Z}^+.\)
Find:
(a) \(\displaystyle{\bigcup_{i=1}^n} A_i= \quad \quad\quad     (b)\displaystyle{\bigcap_{i=1}^n} A_i=\)

Exercise \(\PageIndex{15}\)

Let \(B_i = (0,\frac{1}{i})\) for \(i \in \mathbb{Z}^+.\)
Find:
(a) \(B_1= \quad    (b)\, B_3=  \quad   (c)\, B_6=\)

Answer

(a) \(B_1=(0,1)\quad \quad \quad (b)\, B_3=(0,\frac{1}{3})\quad  \quad \quad (c)\, A_6=(0,\frac{1}{6})\)

Exercise \(\PageIndex{16}\)

Let \(B_i = (0,\frac{1}{i})\) for \(i \in \mathbb{Z}^+.\)
Find:

(a) \(\displaystyle{\bigcup_{i=1}^n} B_i= \quad \quad \quad    (b)\displaystyle{\bigcap_{i=1}^n} B_i=\)

(c) \(\displaystyle{\bigcup_{i=1}^\infty} B_i= \quad \quad \quad    (d)\displaystyle{\bigcap_{i=1}^\infty} B_i=\)