4.5: Index Sets and Partitions
( \newcommand{\kernel}{\mathrm{null}\,}\)
n⋃i=1Ai and n⋂i=1Ai
The notion of union can be extended to three sets: A∪B∪C={x∈U∣(x∈A)∨(x∈B)∨(x∈C)}. It is obvious how to generalize it to the union of any number of sets. We use a notation that resembles the summation notation to describe such a union: n⋃i=1Ai=A1∪A2∪⋯∪An. We define
n⋃i=1Ai={x∈U∣(x∈A1)∨(x∈A2)∨⋯∨(x∈An)}. It looks messy! Here is a better alternative:
n⋃i=1Ai={x∈U∣x∈Ai for somei∈N, where 1≤i≤n}.
In a similar manner, n⋂i=1Ai=A1∩A2∩⋯∩An, and we define
n⋂i=1Ai={x∈U∣x∈Ai for alli∈N, where 1≤i≤n}
In plain English, n⋃i=1Ai is the collection of all elements in the Ai’s, and n⋂i=1An is the collection of all elements common to all Ai’s.
Example 4.5.1
For i=1,2,3,…, let Ai=[−i,i]. First, construct several Ai for comparison, because it may help us detect any specific pattern. See Figure below. It is clear that A1⊂A2⊂⋯. Thus, n⋃i=1Ai=[−n,n]=An, and n⋂i=1Ai=[−1,1]=A1.
hands-on Exercise 4.5.1
Evaluate n⋃i=1Bi and n⋂i=1Bi, where Bi=[0,2i) for i∈N.
∞⋃i=1Ai and ∞⋂i=1Ai
It is obvious that we can also extend the upper bound to infinity. ∞⋃i=1Ai=A1∪A2∪⋯={x∈U∣x∈Ai for somei∈N},∞⋂i=1Ai=A1∩A2∩⋯={x∈U∣x∈Ai for alli∈N}. In some situations, we may borrow the idea of partial sums from calculus. We first find the union or intersection of the first n sets, then take the limit as n approaches infinity. Thus, if the limit is well-defined, the
∞⋃i=1Ai=limn→∞n⋃i=1Ai,and∞⋂i=1Ai=limn→∞n⋂i=1Ai.
Example 4.5.2
Let Ai=[−i,i]. We have learned from the last example that n⋃i=1Ai=[−n,n] and n⋂i=1Ai=[−1,1]. Hence, ∞⋃i=1Ai=limn→∞[−n,n]=(−∞,∞),and∞⋂i=1Ai=[−1,1]. Recall that we write (−∞,∞) instead of [−∞,∞] because ±∞ are not numbers, they are merely symbols representing infinitely large values.
hands-on Exercise 4.5.2
Evaluate ∞⋃i=1Bi and ∞⋂i=1Bi, where Bi=[0,2i).
Example 4.5.3
Let Bi=(0,1−12i]. Determine ∞⋃i=1Bi and ∞⋂i=1Bi.
- Solution
-
Once again, we have B1⊂B2⊂⋯. It is easy to check that n⋃i=1Bi=Bn=(0,1−12n],andn⋂i=1Bi=B1=(0,12]. It follows that ∞⋃i=1Bi=limn→∞(0,1−12n]=(0,1),and∞⋂i=1Bi=(0,12]. Note that limn→∞(0,1−12n]≠(0,1] because the endpoint 1 does not belong to any Bi.
hands-on Exercise 4.5.3
Let Ci=[0,1−1i]. Determine ∞⋃i=1Ci and ∞⋂i=1Ci.
Example 4.5.4
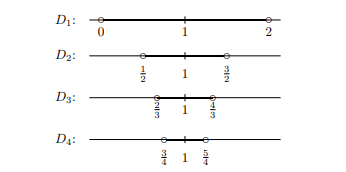
Let Di=(1−1i,1+1i). Determine ∞⋃i=1Di and ∞⋂i=1Di.
hands-on exercise 4.5.4
Let Ei=[−i,1+1i). Determine ∞⋃i=1Ei and ∞⋂i=1Ei.
hands-on Exercise 4.5.5
For each positive integer i, define Fi={i,i+1,i+2,…,3i}. Determine ∞⋃i=1Fi and ∞⋂i=1Fi.
The next two results are obvious.
Theorem 4.5.1
If A1⊆A2⊆A3⊆⋯, then ∞⋂i=1Ai=A1.
Theorem 4.5.2
If A1⊇A2⊇A3⊇⋯, then ∞⋃i=1Ai=A1.
Indexed Family of Sets
How could we describe the union A2∪A4∪A6∪⋯? Well, we can write ⋃ievenAi, which means that union of Ai, where i is even. Since the set of even positive integers is denoted by 2N, another way to describe the same union is ⋃i∈2NAi. It means the union all Ai, where i is taken out from the set 2N. Accordingly, ∞⋃i=0Ai=⋃i∈NAi,and∞⋂i=0Ai=⋂i∈NAi. We can even go one step further, by allowing i to be taken from any set of integers, or any set of real numbers, or even any set of objects. The only restriction is that Ai must exist, and its content must somehow depend on i.
In general, given a nonempty set I, if we could associate with each i∈I a set Ai, we define the indexed family of sets A as A={Ai∣i∈I}. We call I the index set, and define ⋃i∈IAi={x∣x∈Ai for somei∈I},⋂i∈IAi={x∣x∈Ai for alli∈I}. Let us look at a few examples.
Example 4.5.5
To describe the union A1∪A3∪A7∪A11∪A23, we first define the index set to be I={1,3,7,11,23}, which is the set of all the subscripts used in the union. Now the union can be conveniently described as ⋃i∈IAi.
Example 4.5.6
Consider five sets A1={1,4,23},A2={7,11,23},A3={3,6,9},A4={5,17,22},A5={3,6,23}. Let I={2,5}, then ⋃i∈IAi=A2∪A5={7,11,23}∪{3,6,23}={3,6,7,11,23}. Likewise, ⋂i∈IAi=A2∩A5={7,11,23}∩{3,6,23}={23}.
hands-on Exercise 4.5.6
Let J={1,4,5}. Evaluate ⋃i∈JAi and ⋂i∈JAi, where Ais are defined in the last example.
hands-on Exercise 4.5.7
An index set could be a set of any objects. For instance, the sets of numbers in the last example could be the favorite Lotto numbers of five different students. We could index these sets according to the names of the students: AJohn={1,4,23},AMary={7,11,23},AJoe={3,6,9},APete={5,17,22},ALucy={3,6,23}. If I={Mary,Joe,Lucy}, what is ⋃i∈I? How would you interpret its physical meaning?
example 4.5.7
Let I={x∣x is a living human being}, and define Bi={x∈I∣x is a child of i},Ai={i}∪Bi for each i∈I. Then ⋂i∈IAi=∅,⋃i∈IAi=I,⋂i∈IBi=∅, and ⋃i∈IBi=I−{x∣x's parents are both deceased}. We leave it as an exercise to verify these unions and intersections.
hands-on Exercise 4.5.8
Verify the intersection and union in the last example.
hands-onExercise 4.5.9
If I represents a set of students, and Ai represents the set of friends of student i, interpret the meaning of ⋃i∈IAi and ⋂i∈IAi.
We close this section with yet another generalization of De Morgan’s laws.
Theorem 4.5.3 Extended De Morgan's laws
For any nonempty index set I, we have ¯⋃i∈IAi=⋂i∈I¯Ai, and ¯⋂i∈IAi=⋃i∈I¯Ai.
- Proof 1
-
Let x∈¯⋃i∈IAi, then x∉⋃i∈IAi={x∣x∈Ai for somei∈I}. This means x∉Ai for every i∈I. Hence, x∈¯Ai for each i∈I. Consequently, x∈⋂i∈I¯Ai. This proves that ¯⋃i∈IAi⊆⋂i∈I¯Ai.
Next, let x∈⋂i∈I¯Ai. Then x∈¯Ai for each i∈I. This means x∉Ai for each i∈I. Then x∉{x∣x∈Ai for somei∈I}=⋃i∈IAi. Thus, x∈¯⋃i∈IAi, proving that ⋂i∈I¯Ai⊆¯⋃i∈IAi. We proved earlier that ¯⋃i∈IAi⊆⋂i∈I¯Ai. Therefore, the two sets must be equal.
The proof of ¯⋂i∈IAi=⋃i∈I¯Ai proceeds in a similar manner, and is left as an exercise.
- Proof 2
-
We shall prove ¯⋃i∈IAi=⋂i∈I¯Ai. We leave out the explanations for you to fill in: x∈¯⋃i∈IAi⇔¯x∈⋃i∈IAi⇔¯x∈Ai for some i⇔x∉Ai for all i⇔x∈¯Ai for all i⇔x∈⋂i∈I¯Ai. The proof of ¯⋂i∈IAi=⋃i∈I¯Ai is left as an exercise.
Partitions of Sets
Definition: Mutually Disjoint
Sets A1,A2,A3,… are mutually disjoint (or pairwise disjoint) if and only if no two sets with distinct subscripts have any elements in common.
Specifically, for all j=1,2,3,…
Ai∩Aj=∅ whenever i≠j.
Definition: Partition
A finite or infinite collection of non-empty sets {A1,A2,A3,…} is a partition of set A if and only if
(1) A is the union of all the Ai.
(2) The sets {A1,A2,A3,…} are mutually disjoint.
Example 4.5.8
Let S={1,2,3,4,5,6,7,8,9,10}. Which of the following collections of sets are a partition of set S?
(a) A={A1,A2} with A1={1,3,5,7,9},A2={2,4,6,8,10}
(b) B={B1,B2,B3} with B1={1,2,3,4,5,6,9},B2={7},B3={8,9,10}
(c) C={C1,C2,C3,C4} with C1={8,10},C2={3},C3={1,4,9},C4={2,5,6,7},
(d) D={D1,D2,D3,D4} with D1={1},D2={2},D3={3},D4={4},D5={5,6,7,8,9,10},
(e) E={E1,E2} with E1={1,3,5,7,9},E2={0,2,4,6,8,10}
(f) F={F1,F2,F3} with F1={1,2,3,4},F2={5,6,7},F3={9,10}
- Solution
-
(a), (c) & (d)
Summary and Review
- When dealing with arbitrary intersection or union of intervals, first identify the endpoints, then analyze the sets involved in the operation to determine whether an endpoint should be included or excluded.
- Intersection and union can be performed on a group of similar sets identified by subscripts belonging to an index set.
- Consequently, intersection or union can be formed by naming a specific index set.
- A collection of sets can be a partition of a set if it satisfies two conditions.
Exercises
Exercise 4.5.1
For each n∈Z+, define An=(−1n,2n). Find ∞⋂n=1An and ∞⋃n=1An.
- Answer
-
∞⋂n=1An=(0,2), ∞⋃n=1An=(−1,∞).
Exercise 4.5.2
For each n∈Z+, define Bn={m∈Z∣−n2≤m≤3n}. Evaluate ∞⋂n=1Bn and ∞⋃n=1Bn.
Exercise 4.5.3
Define Cn={n,n+1,n+2,…,2n+1} for each integer n≥0. Evaluate ∞⋂n=0Cn and ∞⋃n=0Cn.
- Answer
-
∞⋂n=0Cn=∅, ∞⋃n=0Cn=N∪{0}.
Exercise 4.5.4
For each n∈I={1,2,3,…,100}, define Dn=[−n,2n]∩Z. Evaluate ⋂n∈IDn and ⋃n∈IDn.
Exercise 4.5.5
For each n∈N, define En={−n,−n+1,−n+2,…,n2}. Evaluate ⋂n∈NEn and ⋃n∈NEn.
- Answer
-
⋂n∈NEn=E1={−1,0,1}, ⋃n∈NEn=Z.
Exercise 4.5.6
For each n∈N, define Fn={mn∣m∈Z}. Evaluate ⋂n∈NFn and ⋃n∈NFn.
Exercise 4.5.7
Let I=(0,1), and define Ai=[1,1i] for each i∈I. For instance A0.5=[1,2] and Aπ4=[1,4π]. Evaluate ⋃i∈IAi and ⋂i∈IAi.
- Answer
-
⋃i∈IAi=[1,∞), ⋂i∈IAi={1}.
Exercise 4.5.8
Define I=(0,1), and for each i∈I, let Bi=(−i,1i). Evaluate ⋃i∈IBi=(−1,∞) and ⋂i∈IBi.
Exercise 4.5.9
Evaluate ⋂x∈(1,2)(1−2x,x2) and ⋃x∈(1,2)(1−2x,x2).
- Answer
-
⋂x∈(1,2)(1−2x,x2)=[−1,1], ⋃x∈(1,2)(1−2x,x2)=(−3.4).
Exercise 4.5.10
Evaluate ⋂x∈(0,1)(x,1x) and ⋃x∈(0,1)(x,1x).
Exercise 4.5.11
Let the universal set be R2. For each r∈(0,∞), define Ar={(x,y)∣y=rx2}; that is, Ar is the set of points on the parabola y=rx2, where r>0. Evaluate ⋂r∈(0,∞)Ar and ⋃r∈(0,∞)Ar.
- Answer
-
⋂r∈(0,∞)Ar={(0,0)}, ⋃r∈(0,∞)Ar=R∗×R+∪{(0,0)}.
Exercise 4.5.12
Prove that ¯⋂i∈IAi=⋃i∈I¯Ai for any nonempty index set I.
Exercise 4.5.13
Let Ai=[−1i,5i] for i∈Z+.
Find:
(a) A1=(b)A3=(c)A6=
- Answer
-
(a) A1=[−1,5](b)A3=[−13,15](c)A6=[−16,30]
Exercise 4.5.14
Let Ai=[−1i,5i] for i∈Z+.
Find:
(a) n⋃i=1Ai=(b)n⋂i=1Ai=
Exercise 4.5.15
Let Bi=(0,1i) for i∈Z+.
Find:
(a) B1=(b)B3=(c)B6=
- Answer
-
(a) B1=(0,1)(b)B3=(0,13)(c)A6=(0,16)
Exercise 4.5.16
Let Bi=(0,1i) for i∈Z+.
Find:
(a) n⋃i=1Bi=(b)n⋂i=1Bi=
(c) ∞⋃i=1Bi=(d)∞⋂i=1Bi=