5.2: Definition of Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
Definition: Function
Let A and B be nonempty sets. A function from A to B is a rule that assigns to every element of A a unique element in B. We call A the domain, and B the codomain, of the function. If the function is called f, we write f:A→B. Given x∈A, its associated element in B is called its image under f. In other words, a function is a relation from A to B with the condition that for every element in the domain, there exists a unique image in the codomain (this is really two conditions: existence of an image and uniqueness of an image). We denote it f(x), which is pronounced as “ f of x.”
A function is sometimes called a map or mapping. Hence, we sometimes say f maps x to its image f(x).
Example 5.2.1
The function f:{a,b,c} to {1,3,5,9} is defined according to the rule f(a)=1,f(b)=5,andf(c)=9. It is a well-defined function. The rule of assignment can be summarized in a table: xabcf(x)159 We can also describe the assignment rule pictorially with an arrow diagram, as shown in Figure 6.2.
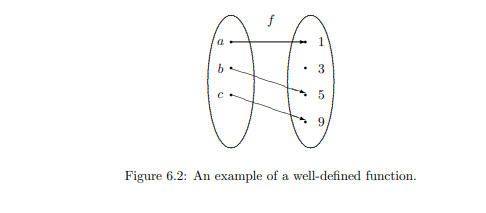
The two key requirements of a function are
- every element in the domain has an image under f, and
- the image is unique.
You may want to remember that every element in A has exactly one “partner” in B.
Example 5.2.2
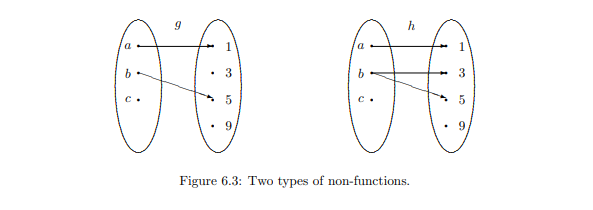
Figure 6.3 depicts two examples of non-functions. In the one on the left, one of the elements in the domain has no image associated with it; thus lacking existence of an image. In the one on the right, one of the elements in the domain has two images assigned to it; thus lacking uniqueness of an image. Both are not functions.
hands-on exercise 5.2.1
Do these rules xabcf(x)533xbcg(x)95xabbch(x)1539 produce functions from {a,b,c} to {1,3,5,9}? Explain.
hands-on exercise 5.2.2
Does the definition r(x)={x if today is Monday, 2x if today is not Monday produce a function from R to R? Explain.
hands-on exercise 5.2.3
Does the definition s(x)={5 if x<2, 7 if x>3, produce a function from R to R? Explain.
Example 5.2.3
The function f:[0,∞)→R is defined by f(x)=√x. Also the function g:[2,∞)→R is defined as g(x)=√x−2. Can you explain why the domain of g is [2,∞)?
Example 5.2.4
Let A denote the set of students taking Discrete Mathematics, and G={A,B,C,D,F}, and ℓ(x) is the final grade of student x in Discrete Mathematics. Every student should receive a final grade, and the instructor has to report one and only one final grade for each student. ℓ:A→G. This is precisely what we call a function.
Example 5.2.5
The function n:P({a,b,c,d})→Z is defined as n(S)=|S|. It evaluates the cardinality of a subset of {a,b,c,d}. For example, n({a,c})=n({b,d})=2. Note that n(∅)=0.
hands-on exercise 5.2.4
Consider Example 5.2.5. What other subsets S of {a,b,c,d} also yield n(S)=2? What are the smallest and the largest images the function n can produce?
Example 5.2.6
Consider a function f:Z7→Z5. The domain and the codomain are,
Z7={0,1,2,3,4,5,6},andZ5={0,1,2,3,4},
respectively. Not only are their elements different, their binary operations are different too. In the domain Z7, the arithmetic is performed modulo 7, but the arithmetic in the codomain Z5 is done modulo 5. So we need to be careful in describing the rule of assignment if a computation is involved. We could say, for example,
f(x)=z,where z≡3x(mod5).
Consequently, starting with any element x in Z7, we consider x as an ordinary integer, multiply by 3, and reduce the answer modulo 5 to obtain the image f(x). For brevity, we shall write
f(x)≡3x(mod5).
We summarize the images in the following table:
n0123456f(n)0314203
Take note that the images start repeating after f(4)=2.
hands-on exercise 5.2.5
Tabulate the images of g:Z10→Z5 defined by g(x)≡3x(mod5).
Definition: A Function as a Set of Ordered Pairs
A function f:A→B can be written as a set of ordered pairs (x,y) from A×B such that y=f(x).
A function is, by definition, a set of ordered pairs, with certain restrictions.
Example 5.2.7
The function f in Example 5.26 can be written as the set of ordered pairs {(0,0),(1,3),(2,1),(3,4),(4,2),(5,0),(6,3)}. If one insists, we could display the graph of a function using an xy-plane that resembles the usual Cartesian plane. Keep in mind: the elements x and y come from A and B, respectively. We can “plot” the graph for f in Example 5.26 as shown below.
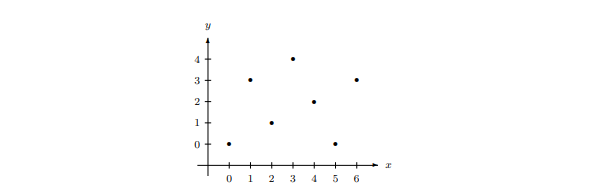
Besides using a graphical representation, we can also use a (0,1)-matrix. A (0,1)-matrix is a matrix whose entries are 0 and 1. For the function f, we use a 7×5 matrix, whose rows and columns correspond to the elements of A and B, respectively, and put one in the (i,j)th entry if j=f(i), and zero otherwise. The resulting matrix is
012340123456(10000000100100000001001001000000010)
We call it the incidence matrix for the function f.
hands-on exercise 5.2.6
"Plot” the graph of g in Hands-On Exercise 5.2.5
Summary and Review
- A function f from a set A to a set B (called the domain and the codomain, respectively) is a rule that describes how a value in the codomain B is assigned to an element from the domain A.
- But it is not just any rule; rather, the rule must assign to every element x in the domain a unique value in the codomain.
- This unique value is called the image of x under the function f, and is denoted f(x).
- We use the notation f:A→B to indicate that the name of the function is f, the domain is A, and the codomain is B.
- A function f:A→B is the collection of all ordered pairs (x,y) from A×B such that y=f(x).
- The graph of a function may not be a curve, as in the case of a real function. It can be just a collection of points.
- We can also display the images of a function in a table, or represent the function with an incidence matrix.
Exercises
exercise 5.2.1
What subset A of R would you use to make f:A→R defined by f(x)=√3x−7 a function?
- Answer
-
[73,∞)
exercise 5.2.2
What subset A of R would you use to make
- g:A→R, where g(x)=√(x−3)(x−7)
- h:A→R, where h(x)=x+2√(x−2)(5−x)
functions?
exercise 5.2.3
Which of these data support a function from {1,2,3,4} to {1,2,3,4}? Explain.
x123f(x)342x1234g(x)2432x12334h(x)24323
- Answer
-
Only g is a function. The image f(4) is undefined, and there are two values for h(3). Hence, both f and h are not well-defined functions.
exercise 5.2.4
(a) Use arrow diagrams to show three different functions from {1,2,3,4} to {1,2,3,4}.
(b) How many different functions from {1,2,3,4} to {1,2,3,4} are possible?
exercise 5.2.5
Determine whether these are functions. Explain.
- f:R→R, where f(x)=3x2+5.
- g:(5,∞)→R, where g(x)=7√x−4.
- h:R→R, where h(x)=−√7−4x+4x2.
- Answer
-
(a) Yes, because no division by zero will ever occur.
exercise 5.2.6
Determine whether these are functions. Explain.
- s:R→R, where x2+[s(x)]2=9.
- t:R→R, where |x−t(x)|=4.
exercise 5.2.7
Use arrow diagrams to show two different functions from {a,b,c,d} to {1,2,3,4,5,6}.
- Answer
-
answers will vary
exercise 5.2.8
Let T be your family tree that includes your biological mother, your maternal grandmother, your maternal great-grandmother, and so on, and all of their female descendants. Determine which of the following define a function from T to T.
- h1:T→T, where h1(x) is the mother of x.
- h2:T→T, where h2(x) is x’s sister.
- h3:T→T, where h3(x) is an aunt of x.
- h4:T→T, where h4(x) is the eldest daughter of x’s maternal grandmother.
exercise 5.2.9
For each of the following functions, determine the image of the given x.
- k1:N−{1}→N, k1(x)=smallest prime factor of x, x=217.
- k2:Z11→Z11, k2(x)≡3x (mod 11), x=6.
- k3:Z15→Z15, k3(x)≡3x (mod 15), x=6.
- Answer
-
(a) 7 (b) 7 (c) 3
exercise 5.2.10
For each of the following functions, determine the images of the given x-values.
- ℓ1:Z→Z, ℓ1(x)=xmod, x=250, x=0, and x=-16.
Remark: Recall that, without parentheses, the notation “mod” means the binary operation mod.
{\ell_2}:{\mathbb{Z}}\to{\mathbb{Z}}, \ell_2(x)=\gcd(x,24), x=100, x=0, and x=-21.


