5.2: Definition of Functions

Definition: Function

Let $A$ and $B$ be nonempty sets. A function from $A$ to $B$ is a rule that assigns to every element of $A$ a unique element in $B$. We call $A$ the domain, and $B$ the codomain, of the function. If the function is called $f$, we write $f :A \to B$. Given $x\in A$, its associated element in $B$ is called its image under $f$. In other words, a function is a relation from $A$ to $B$ with the condition that for every element in the domain, there exists a unique image in the codomain (this is really two conditions: existence of an image and uniqueness of an image). We denote it $f(x)$, which is pronounced as “ $f$ of $x$.”

A function is sometimes called a map or mapping. Hence, we sometimes say $f$ maps $x$ to its image $f(x)$.

Example $\PageIndex{1}\label{eg:defnfcn-01}$

The function $f:\{a,b,c\}$ to $\{1,3,5,9\}$ is defined according to the rule $$f(a)=1, \qquad f(b)=5, \qquad\mbox{and}\qquad f(c) = 9.$$ It is a well-defined function. The rule of assignment can be summarized in a table: $$\begin{array}{|c||c|c|c|} \hline x & a & b & c \\ \hline f(x)& 1 & 5 & 9 \\ \hline \end{array}$$ We can also describe the assignment rule pictorially with an arrow diagram, as shown in Figure 6.2.

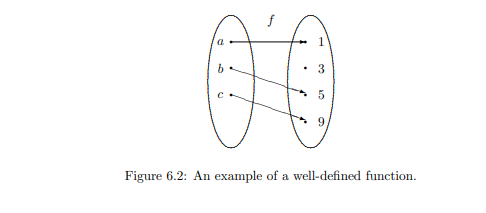
The two key requirements of a function are

• every element in the domain has an image under $f$, and
• the image is unique.

You may want to remember that every element in $A$ has exactly one “partner” in $B$.

Example $\PageIndex{2}\label{eg:defnfcn-02}$

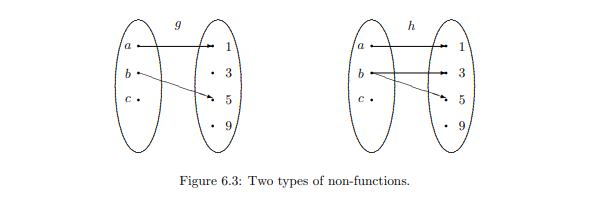
Figure 6.3 depicts two examples of non-functions. In the one on the left, one of the elements in the domain has no image associated with it; thus lacking existence of an image. In the one on the right, one of the elements in the domain has two images assigned to it; thus lacking uniqueness of an image. Both are not functions.

hands-on exercise $\PageIndex{1}\label{he:defnfcn-01}$

Do these rules $$\begin{array}{|c||c|c|c|} \hline x & a & b & c \\ \hline f(x)& 5 & 3 & 3 \\ \hline \end{array} \hskip0.75in \begin{array}{|c||c|c|} \hline x & b & c \\ \hline g(x)& 9 & 5 \\ \hline \end{array} \hskip0.75in \begin{array}{|c||c|c|c|c|} \hline x & a & b & b & c \\ \hline h(x)& 1 & 5 & 3 & 9 \\ \hline \end{array}$$ produce functions from $\{a,b,c\}$ to $\{1,3,5,9\}$? Explain.

hands-on exercise $\PageIndex{2}\label{he:defnfcn-02}$

Does the definition $$r(x) = \cases{ x & if today is Monday, \cr 2x & if today is not Monday \cr}$$ produce a function from $\mathbb{R}$ to $\mathbb{R}$? Explain.

hands-on exercise $\PageIndex{3}\label{he:defnfcn-03}$

Does the definition $$s(x) = \cases{ 5 & if $x<2$, \cr 7 & if $x>3$, \cr}$$ produce a function from $\mathbb{R}$ to $\mathbb{R}$? Explain.

Example $\PageIndex{3}\label{eg:defnfcn-03}$

The function $f:{[0,\infty)}\to{\mathbb{R}}$ is defined by $$f(x) = \sqrt{x}.$$   Also the function ${g}:{[2,\infty)}\to{\mathbb{R}}$ is defined as $$g(x) = \sqrt{x-2}.$$ Can you explain why the domain of $g$ is $[2,\infty)$?

Example $\PageIndex{4}\label{eg:defnfcn-04}$

Let $A$ denote the set of students taking Discrete Mathematics, and $G=\{A,B,C,D,F\}$, and $\ell(x)$ is the final grade of student $x$ in Discrete Mathematics. Every student should receive a final grade, and the instructor has to report one and only one final grade for each student. $\ell:A \to G.$  This is precisely what we call a function.

Example $\PageIndex{5}\label{eg:defnfcn-05}$

The function ${n}:{\mathscr{P}(\{a,b,c,d\})}\to{\mathbb{Z}}$ is defined as $n(S)=|S|$. It evaluates the cardinality of a subset of $\{a,b,c,d\}$. For example, $$n\big(\{a,c\}\big) = n\big(\{b,d\}\big) = 2.$$ Note that $n(\emptyset)=0$.

hands-on exercise $\PageIndex{4}\label{he:defnfcn-04}$

Consider Example 5.2.5.  What other subsets $S$ of $\{a,b,c,d\}$ also yield $n(S)=2$? What are the smallest and the largest images the function $n$ can produce?

Example $\PageIndex{6}\label{eg:defnfcn-06}$

Consider a function ${f}:{\mathbb{Z}_7}\to{\mathbb{Z}_5}$. The domain and the codomain are,

$$\mathbb{Z}_7 = \{0,1,2,3,4,5,6\}, \qquad\mbox{and}\qquad \mathbb{Z}_5 = \{0,1,2,3,4\},$$

respectively. Not only are their elements different, their binary operations are different too. In the domain $\mathbb{Z}_7$, the arithmetic is performed modulo 7, but the arithmetic in the codomain $\mathbb{Z}_5$ is done modulo 5. So we need to be careful in describing the rule of assignment if a computation is involved. We could say, for example,

$$f(x) = z, \quad\mbox{where } z \equiv 3x \pmod{5}.$$

Consequently, starting with any element $x$ in $\mathbb{Z}_7$, we consider $x$ as an ordinary integer, multiply by 3, and reduce the answer modulo 5 to obtain the image $f(x)$. For brevity, we shall write

$$f(x) \equiv 3x \pmod{5}.$$

We summarize the images in the following table:

$$\begin{array}{|c||*{7}{c|}} \hline n & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline f(n) & 0 & 3 & 1 & 4 & 2 & 0 & 3 \\ \hline \end{array}$$

Take note that the images start repeating after $f(4)=2$.

hands-on exercise $\PageIndex{5}\label{he:defnfcn-05}$

Tabulate the images of ${g}:{\mathbb{Z}_{10}}\to{\mathbb{Z}_5}$ defined by $$g(x) \equiv 3x \pmod{5}.$$

Definition: A Function as a Set of Ordered Pairs

A function ${f}:{A}\to{B}$ can be written as a set of ordered pairs $(x,y)$ from $A\times B$ such that $y=f(x)$.

 A function is, by definition, a set of ordered pairs, with certain restrictions.

Example $\PageIndex{7}\label{eg:defnfcn-07}$

The function $f$ in Example 5.26 can be written as the set of ordered pairs $$\{(0,0), (1,3), (2,1), (3,4), (4,2), (5,0), (6,3)\}.$$ If one insists, we could display the graph of a function using an $xy$-plane that resembles the usual Cartesian plane. Keep in mind: the elements $x$ and $y$ come from $A$ and $B$, respectively. We can “plot” the graph for $f$ in Example 5.26 as shown below.

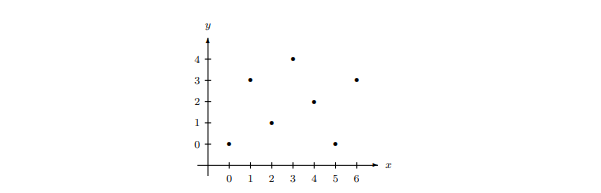
Besides using a graphical representation, we can also use a $(0,1)$-matrix. A $(0,1)$-matrix is a matrix whose entries are 0 and 1. For the function $f$, we use a $7\times5$ matrix, whose rows and columns correspond to the elements of $A$ and $B$, respectively, and put one in the $(i,j)$th entry if $j=f(i)$, and zero otherwise. The resulting matrix is

$$\begin{array}{cc} & \begin{array}{ccccc} 0 & 1 & 2 & 3 & 4 \end{array} \\ \begin{array}{c} 0 \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \end{array} & \left(\begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{array}\right) \end{array}$$

We call it the incidence matrix for the function $f$.

hands-on exercise $\PageIndex{6}\label{he:defnfcn-06}$

"Plot” the graph of $g$ in Hands-On Exercise 5.2.5

Summary and Review

• A function $f$ from a set $A$ to a set $B$ (called the domain and the codomain, respectively) is a rule that describes how a value in the codomain $B$ is assigned to an element from the domain $A$.
• But it is not just any rule; rather, the rule must assign to every element $x$ in the domain a unique value in the codomain.
• This unique value is called the image of $x$ under the function $f$, and is denoted $f(x)$.
• We use the notation ${f}:{A}\to{B}$ to indicate that the name of the function is $f$, the domain is $A$, and the codomain is $B$.
• A function ${f}:{A}\to{B}$ is the collection of all ordered pairs $(x,y)$ from $A\times B$ such that $y=f(x)$.
• The graph of a function may not be a curve, as in the case of a real function. It can be just a collection of points.
• We can also display the images of a function in a table, or represent the function with an incidence matrix.

Exercises 

exercise $\PageIndex{1}\label{ex:defnfcn-01}$

What subset $A$ of $\mathbb{R}$ would you use to make ${f}:{A}\to{\mathbb{R}}$ defined by $f(x) = \sqrt{3x-7}$ a function?

Answer

$\big[\frac{7}{3},\infty\big)$

exercise $\PageIndex{2}\label{ex:defnfcn-02}$

What subset $A$ of $\mathbb{R}$ would you use to make

1. ${g}:{A}\to{\mathbb{R}}$, where $g(x) = \sqrt{(x-3)(x-7)}$
2. ${h}:{A}\to{\mathbb{R}}$, where $h(x) = \frac{x+2}{\sqrt{(x-2)(5-x)}}$

 functions?

exercise $\PageIndex{3}\label{ex:defnfcn-03}$

Which of these data support a function from $\{1,2,3,4\}$ to $\{1,2,3,4\}$? Explain.

$$\begin{array}{|c||c|c|c|} \hline x & 1 & 2 & 3 \\ \hline f(x) & 3 & 4 & 2 \\ \hline \end{array} \hskip0.4in \begin{array}{|c||c|c|c|c|} \hline x & 1 & 2 & 3 & 4 \\ \hline g(x) & 2 & 4 & 3 & 2 \\ \hline \end{array} \hskip0.4in \begin{array}{|c||c|c|c|c|c|} \hline x & 1 & 2 & 3 & 3 & 4 \\ \hline h(x) & 2 & 4 & 3 & 2 & 3 \\ \hline \end{array}$$
 

Answer

Only $g$ is a function. The image $f(4)$ is undefined, and there are two values for $h(3)$. Hence, both $f$ and $h$ are not well-defined functions.

exercise $\PageIndex{4}\label{ex:defnfcn-04}$

(a) Use arrow diagrams to show three different functions from $\{1,2,3,4\}$ to $\{1,2,3,4\}$.
(b) How many different functions from $\{1,2,3,4\}$ to $\{1,2,3,4\}$ are possible? 

exercise $\PageIndex{5}\label{ex:defnfcn-05}$

Determine whether these are functions. Explain.

1. ${f}:{\mathbb{R}}\to{\mathbb{R}}$, where $f(x) = \frac{3}{x^2+5}$.
2. ${g}:{(5,\infty)}\to{\mathbb{R}}$, where $g(x) = \frac{7}{\sqrt{x-4}}$.
3. ${h}:{\mathbb{R}}\to{\mathbb{R}}$, where $h(x) = -\sqrt{7-4x+4x^2}$.

Answer

(a) Yes, because no division by zero will ever occur.

exercise $\PageIndex{6}\label{ex:defnfcn-06}$

Determine whether these are functions. Explain.

1. ${s}:{\mathbb{R}}\to{\mathbb{R}}$, where $x^2+[s(x)]^2=9$.
2. ${t}:{\mathbb{R}}\to{\mathbb{R}}$, where $|x-t(x)|=4$.

exercise $\PageIndex{7}\label{ex:defnfcn-07}$

Use arrow diagrams to show two different functions from $\{a,b,c,d\}$ to $\{1,2,3,4,5,6\}$.

 

Answer

answers will vary

exercise $\PageIndex{8}\label{ex:defnfcn-08}$

Let $T$ be your family tree that includes your biological mother, your maternal grandmother, your maternal great-grandmother, and so on, and all of their female descendants. Determine which of the following define a function from $T$ to $T$.

1. ${h_1}:{T}\to{T}$, where $h_1(x)$ is the mother of $x$.
2. ${h_2}:{T}\to{T}$, where $h_2(x)$ is $x$’s sister.
3. ${h_3}:{T}\to{T}$, where $h_3(x)$ is an aunt of $x$.
4. ${h_4}:{T}\to{T}$, where $h_4(x)$ is the eldest daughter of $x$’s maternal grandmother.

exercise $\PageIndex{9}\label{ex:defnfcn-09}$

For each of the following functions, determine the image of the given $x$.

1. ${k_1}:{\mathbb{N}-\{1\}}\to{\mathbb{N}}$, $k_1(x)=\mbox{smallest prime factor of }x$, $x=217$.
2. ${k_2}:{\mathbb{Z}_{11}}\to{\mathbb{Z}_{11}}$, $k_2(x)\equiv3x$ (mod 11), $x=6$.
3. ${k_3}:{\mathbb{Z}_{15}}\to{\mathbb{Z}_{15}}$, $k_3(x)\equiv3x$ (mod 15), $x=6$.

Answer

(a) 7 (b) 7 (c) 3

exercise $\PageIndex{10}\label{ex:defnfcn-10}$

For each of the following functions, determine the images of the given $x$-values.

• ${\ell_1}:{\mathbb{Z}}\to{\mathbb{Z}}$, $\ell_1(x)=x\bmod7$, $x=250$, $x=0$, and $x=-16$.

Remark: Recall that, without parentheses, the notation “mod” means the binary operation mod.

${\ell_2}:{\mathbb{Z}}\to{\mathbb{Z}}$, $\ell_2(x)=\gcd(x,24)$, $x=100$, $x=0$, and $x=-21$.