2.6E: Exercises
- Last updated
- Jan 7, 2020
- Save as PDF
- Page ID
- 30934
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
Solve Proportions
In the following exercises, solve.
Example 2.6E.31
x56=78
- Answer
-
49
Example 2.6E.32
n91=813
Example 2.6E.32
4963=z9
- Answer
-
7
Example 2.6E.33
5672=y9
Example 2.6E.34
5a=6511
- Answer
-
9
Example 2.6E.35
4b=64144
Example 2.6E.36
98154=−7p
- Answer
-
−11
Example 2.6E.37
72156=−6q
Example 2.6E.38
a−8=−4248
- Answer
-
7
Example 2.6E.39
b−7=−3042
Example 2.6E.40
2.7j=0.90.2
- Answer
-
0.6
Example 2.6E.41
2.8k=2.11.5
Example 2.6E.42
aa+12=47
- Answer
-
16
Example 2.6E.43
bb−16=119
Example 2.6E.44
cc−104=−58
- Answer
-
−58
Example 2.6E.45
dd−48=−133
Example 2.6E.46
m+9025=m+3015
- Answer
-
60
Example 2.6E.47
n+104=40−n6
Example 2.6E.48
2p+48=p+186
- Answer
-
30
Example 2.6E.49
q−22=2q−718
Example 2.6E.50
Pediatricians prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Jocelyn, who weighs 45 pounds?
- Answer
-
9 ml
Example 2.6E.51
Brianna, who weighs 6 kg, just received her shots and needs a pain killer. The pain killer is prescribed for children at 15 milligrams (mg) for every 1 kilogram (kg) of the child’s weight. How many milligrams will the doctor prescribe?
Example 2.6E.52
A veterinarian prescribed Sunny, a 65 pound dog, an antibacterial medicine in case an infection emerges after her teeth were cleaned. If the dosage is 5 mg for every pound, how much medicine was Sunny given?
- Answer
-
325 mg
Example 2.6E.53
Belle, a 13 pound cat, is suffering from joint pain. How much medicine should the veterinarian prescribe if the dosage is 1.8 mg per pound?
Example 2.6E.54
A new energy drink advertises 106 calories for 8 ounces. How many calories are in 12 ounces of the drink?
- Answer
-
159 calories
Example 2.6E.55
One 12 ounce can of soda has 150 calories. If Josiah drinks the big 32 ounce size from the local mini-mart, how many calories does he get?
Example 2.6E.56
A new 7 ounce lemon ice drink is advertised for having only 140 calories. How many ounces could Sally drink if she wanted to drink just 100 calories?
- Answer
-
5 oz
Example 2.6E.57
Reese loves to drink healthy green smoothies. A 16 ounce serving of smoothie has 170 calories. Reese drinks 24 ounces of these smoothies in one day. How many calories of smoothie is he consuming in one day?
Example 2.6E.58
Janice is traveling to Canada and will change $250 US dollars into Canadian dollars. At the current exchange rate, $1 US is equal to $1.01 Canadian. How many Canadian dollars will she get for her trip?
- Answer
-
252.5 Canadian dollars
Example 2.6E.59
Todd is traveling to Mexico and needs to exchange $450 into Mexican pesos. If each dollar is worth 12.29 pesos, how many pesos will he get for his trip?
Example 2.6E.60
Steve changed $600 into 480 Euros. How many Euros did he receive for each US dollar?
- Answer
-
0.80 Euros
Example 2.6E.61
Martha changed $350 US into 385 Australian dollars. How many Australian dollars did she receive for each US dollar?
Example 2.6E.62
When traveling to Great Britain, Bethany exchanged her $900 into 570 British pounds. How many pounds did she receive for each American dollar?
- Answer
-
0.63 British pounds
Example 2.6E.63
A missionary commissioned to South Africa had to exchange his $500 for the South African Rand which is worth 12.63 for every dollar. How many Rand did he have after the exchange?
Example 2.6E.64
Ronald needs a morning breakfast drink that will give him at least 390 calories. Orange juice has 130 calories in one cup. How many cups does he need to drink to reach his calorie goal?
- Answer
-
3 cups
Example 2.6E.65
Sarah drinks a 32-ounce energy drink containing 80 calories per 12 ounce. How many calories did she drink?
Example 2.6E.66
Elizabeth is returning to the United States from Canada. She changes the remaining 300 Canadian dollars she has to $230.05 in American dollars. What was $1 worth in Canadian dollars?
- Answer
-
1.30 Canadian dollars
Example 2.6E.67
Ben needs to convert $1000 to the Japanese Yen. One American dollar is worth 123.3 Yen. How much Yen will he have?
Example 2.6E.68
A golden retriever weighing 85 pounds has diarrhea. His medicine is prescribed as 1 teaspoon per 5 pounds. How much medicine should he be given?
- Answer
-
17 tsp
Example 2.6E.69
Five-year-old Lacy was stung by a bee. The dosage for the anti-itch liquid is 150 mg for her weight of 40 pounds. What is the dosage per pound?
Example 2.6E.70
Karen eats 12 cup of oatmeal that counts for 2 points on her weight loss program. Her husband, Joe, can have 3 points of oatmeal for breakfast. How much oatmeal can he have?
- Answer
-
34 cup
Example 2.6E.71
An oatmeal cookie recipe calls for 12 cup of butter to make 4 dozen cookies. Hilda needs to make 10 dozen cookies for the bake sale. How many cups of butter will she need?
Solve Similar Figure Applications
In the following exercises, ΔABC is similar to ΔXYZ
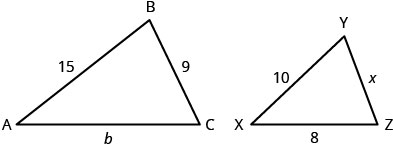
Example 2.6E.72
side b
- Answer
-
12
Example 2.6E.73
side x
In the following exercises, ΔDEF is similar to ΔNPQ

Example 2.6E.74
Find the length of side d.
- Answer
-
7718
Example 2.6E.75
Find the length of side q.
In the following two exercises, use the map shown. On the map, New York City, Chicago, and Memphis form a triangle whose sides are shown in the figure below. The actual distance from New York to Chicago is 800 miles.
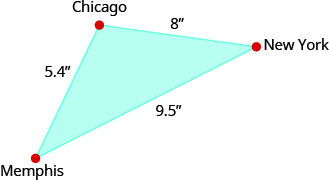
Example 2.6E.76
Find the actual distance from New York to Memphis.
- Answer
-
950 miles
Example 2.6E.77
Find the actual distance from Chicago to Memphis.
In the following two exercises, use the map shown. On the map, Atlanta, Miami, and New Orleans form a triangle whose sides are shown in the figure below. The actual distance from Atlanta to New Orleans is 420 miles.
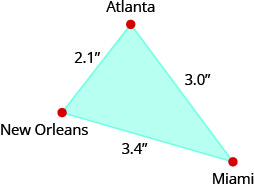
Example 2.6E.78
Find the actual distance from New Orleans to Miami.
- Answer
-
680 miles
Example 2.6E.79
Find the actual distance from Atlanta to Miami.
Example 2.6E.80
A 2 foot tall dog casts a 3 foot shadow at the same time a cat casts a one foot shadow. How tall is the cat?
- Answer
-
23 foot (8in)
Example 2.6E.81
Larry and Tom were standing next to each other in the backyard when Tom challenged Larry to guess how tall he was. Larry knew his own height is 6.5 feet and when they measured their shadows, Larry’s shadow was 8 feet and Tom’s was 7.75 feet long. What is Tom’s height?
Example 2.6E.82
The tower portion of a windmill is 212 feet tall. A six foot tall person standing next to the tower casts a seven foot shadow. How long is the windmill’s shadow?
- Answer
-
247.3 feet
Example 2.6E.83
The height of the Statue of Liberty is 305 feet. Nicole, who is standing next to the statue, casts a 6 foot shadow and she is 5 feet tall. How long should the shadow of the statue be?
Everyday Math
Example 2.6E.84
Heart Rate At the gym, Carol takes her pulse for 10 seconds and counts 19 beats.
- How many beats per minute is this?
- Has Carol met her target heart rate of 140 beats per minute?
- Answer
-
- 114 beats per minute
- no
Example 2.6E.85
Heart Rate Kevin wants to keep his heart rate at 160 beats per minute while training. During his workout he counts 27 beats in 10 seconds.
- How many beats per minute is this?
- Has Kevin met his target heart rate?
Example 2.6E.86
Cost of a Road Trip Jesse’s car gets 30 miles per gallon of gas.
- If Las Vegas is 285 miles away, how many gallons of gas are needed to get there and then home?
- If gas is $3.09 per gallon, what is the total cost of the gas for the trip?
- Answer
-
- 19 gallons
- $58.71
Example 2.6E.87
Cost of a Road Trip Danny wants to drive to Phoenix to see his grandfather. Phoenix is 370 miles from Danny’s home and his car gets 18.5 miles per gallon.
- How many gallons of gas will Danny need to get to and from Phoenix?
- If gas is $3.19 per gallon, what is the total cost for the gas to drive to see his grandfather?
Example 2.6E.88
Lawn Fertilizer Phil wants to fertilize his lawn. Each bag of fertilizer covers about 4,000 square feet of lawn. Phil’s lawn is approximately 13,500 square feet. How many bags of fertilizer will he have to buy?
- Answer
-
4 bags
Example 2.6E.89
House Paint April wants to paint the exterior of her house. One gallon of paint covers about 350 square feet, and the exterior of the house measures approximately 2000 square feet. How many gallons of paint will she have to buy?
Example 2.6E.90
Cooking Natalia’s pasta recipe calls for 2 pounds of pasta for 1 quart of sauce. How many pounds of pasta should Natalia cook if she has 2.5 quarts of sauce?
- Answer
-
5
Example 2.6E.91
Heating Oil A 275 gallon oil tank costs $400 to fill. How much would it cost to fill a 180 gallon oil tank?
Writing Exercises
Example 2.6E.92
Marisol solves the proportion 144a=94 by ‘cross multiplying’, so her first step looks like 4·144=9·a. Explain how this differs from the method of solution shown in Example.
- Answer
-
Answers will vary.
Example 2.6E.93
Find a printed map and then write and solve an application problem similar to Example.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?


