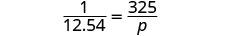8.7: Solve Proportion and Similar Figure Applications
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Solve proportions
- Solve similar figure applications
Before you get started, take this readiness quiz.
If you miss a problem, go back to the section listed and review the material.
- Solve n3=30.
If you missed this problem, review Exercise 2.2.25. - The perimeter of a triangular window is 23 feet. The lengths of two sides are ten feet and six feet. How long is the third side?
If you missed this problem, review Example 3.4.2
Solve Proportions
When two rational expressions are equal, the equation relating them is called a proportion.
A proportion is an equation of the form ab=cd, where b≠0, d≠0.
The proportion is read “a is to b, as c is to d"
The equation 12=48 is a proportion because the two fractions are equal.
The proportion 12=48 is read “1 is to 2 as 4 is to 8.”
Proportions are used in many applications to ‘scale up’ quantities. We’ll start with a very simple example so you can see how proportions work. Even if you can figure out the answer to the example right away, make sure you also learn to solve it using proportions.
Suppose a school principal wants to have 1 teacher for 20 students. She could use proportions to find the number of teachers for 60 students. We let x be the number of teachers for 60 students and then set up the proportion:
1teacher20students=xteachers60students
We are careful to match the units of the numerators and the units of the denominators—teachers in the numerators, students in the denominators.
Since a proportion is an equation with rational expressions, we will solve proportions the same way we solved equations in Solve Rational Equations. We’ll multiply both sides of the equation by the LCD to clear the fractions and then solve the resulting equation.
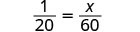 |
|
| Multiply both sides by the LCD, 60. | 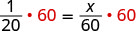 |
| Simplify. | 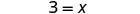 |
| The principal needs 3 teachers for 60 students. |
Now we’ll do a few examples of solving numerical proportions without any units. Then we will solve applications using proportions.
x63=47.
Solution
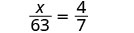 |
||
| To isolate x, multiply both sides by the LCD, 63. | 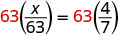 |
|
| Simplify. | 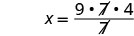 |
|
| Divide the common factors. | 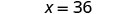 |
|
| Check. To check our answer, we substitute into the original proportion. | ||
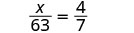 |
||
 |
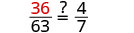 |
|
| Show common factors. | 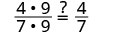 |
|
| Simplify. | 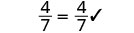 |
n84=1112.
- Answer
-
77
y96=1312.
- Answer
-
104
144a=94.
Solution
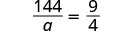 |
||
| Multiply both sides by the LCD. | 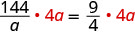 |
|
| Remove common factors on each side. | 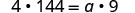 |
|
| Simplify. | 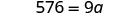 |
|
| Divide both sides by 9. | 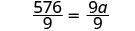 |
|
| Simplify. | 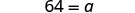 |
|
| Check. | ||
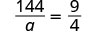 |
||
 |
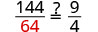 |
|
| Show common factors. | 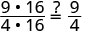 |
|
| Simplify. | 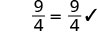 |
91b=75.
- Answer
-
65
39c=138.
- Answer
-
24
nn+14=57.
Solution
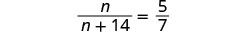 |
||
| Multiply both sides by the LCD. | 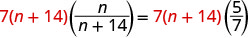 |
|
| Remove common factors on each side. | 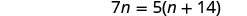 |
|
| Simplify. | 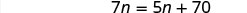 |
|
| Solve for n. | 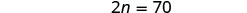 |
|
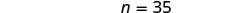 |
||
| Check. | ||
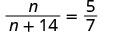 |
||
 |
3535+14?=57 | |
| Simplify. | 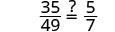 |
|
| Show common factors. | 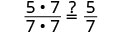 |
|
| Simplify. | 57=57✓ |
yy+55=38.
- Answer
-
33
zz−84=−15.
- Answer
-
14
p+129=p−126.
Solution
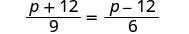 |
||
| Multiply both sides by the LCD, 18. | 18⋅p+129=18⋅p+126 | |
| Simplify. | 2(p+12)=3(p−12) | |
| Distribute. | 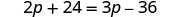 |
|
| Solve fpr p. | 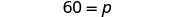 |
|
| Check. | ||
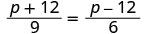 |
||
 |
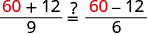 |
|
| Simplify. | 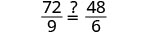 |
|
| Divide. | 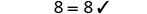 |
v+308=v+6612.
- Answer
-
42
2x+159=7x+315.
- Answer
-
6
To solve applications with proportions, we will follow our usual strategy for solving applications. But when we set up the proportion, we must make sure to have the units correct—the units in the numerators must match and the units in the denominators must match.
When pediatricians prescribe acetaminophen to children, they prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of the child’s weight. If Zoe weighs 80 pounds, how many milliliters of acetaminophen will her doctor prescribe?
Solution
| Identify what we are asked to find, and choose a variable to represent it. | How many ml of acetaminophen will the doctor prescribe? |
| Let a=ml of acetaminophen. | |
| Write a sentence that gives the information to find it. | If 5 ml is prescribed for every 25 pounds, how much will be prescribed for 80 pounds? |
Translate into a proportion–be careful of the units.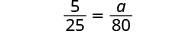 |
|
| Multiply both sides by the LCD, 400. | 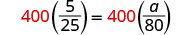 |
| Remove common factors on each side. | 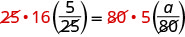 |
| Simplify, but don't multiply on the left. Notice what the next step will be. | 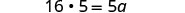 |
| Solve for a. | 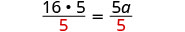 |
| Check. | 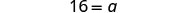 |
| Is the answer reasonable? | |
| Yes, since 80 is about 3 times 25, the medicine should be about 3 times 5. So 16 ml makes sense. | |
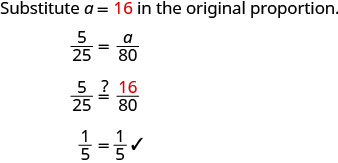 |
|
| Write a complete sentence. | The pediatrician would prescribe 16 ml of acetaminophen to Zoe. |
Pediatricians prescribe 5 milliliters (ml) of acetaminophen for every 25 pounds of a child’s weight. How many milliliters of acetaminophen will the doctor prescribe for Emilia, who weighs 60 pounds?
- Answer
-
12 ml
For every 1 kilogram (kg) of a child’s weight, pediatricians prescribe 15 milligrams (mg) of a fever reducer. If Isabella weighs 12 kg, how many milligrams of the fever reducer will the pediatrician prescribe?
- Answer
-
180 ml
A 16-ounce iced caramel macchiato has 230 calories. How many calories are there in a 24-ounce iced caramel macchiato?
Solution
| Identify what we are asked to find, and choose a variable to represent it. | How many calories are in a 24 ounce iced caramel macchiato? |
| Let c=calories in 24 ounces. | |
| Write a sentence that gives the information to find it. | If there are 230 calories in 16 ounces, then how many calories are in 24 ounces? |
Translate into a proportion–be careful of the units.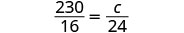 |
|
| Multiply both sides by the LCD, 48. | 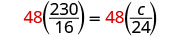 |
| Remove common factors on each side. | 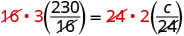 |
| Simplify. | 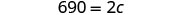 |
| Solve for c. | 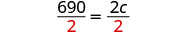 |
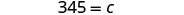 |
|
| Check. | |
| Is the answer reasonable? | |
| Yes, 345 calories for 24 ounces is more than 290 calories for 16 ounces, but not too much more. | |
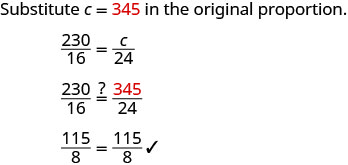 |
|
| Write a complete sentence. | There are 345 calories in a 24-ounce iced caramel macchiato. |
At a fast-food restaurant, a 22-ounce chocolate shake has 850 calories. How many calories are in their 12-ounce chocolate shake? Round your answer to nearest whole number.
- Answer
-
464 calories
Yaneli loves Starburst candies, but wants to keep her snacks to 100 calories. If the candies have 160 calories for 8 pieces, how many pieces can she have in her snack?
- Answer
-
5 pieces
Josiah went to Mexico for spring break and changed $325 dollars into Mexican pesos. At that time, the exchange rate had $1 US is equal to 12.54 Mexican pesos. How many Mexican pesos did he get for his trip?
Solution
| What are you asked to find? | How many Mexican pesos did Josiah get? |
| Assign a variable. | Let p=the number of Mexican pesos. |
| Write a sentence that gives the information to find it. | If $1 US is equal to 12.54 Mexican pesos, then $325 is how many pesos? |
|
Translate into a proportion–be careful of the units.
|
|
| Multiply both sides by the LCD, 12.54p. | 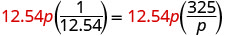 |
| Remove common factors on each side. | 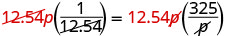 |
| Simplify. | 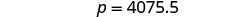 |
| Check. | |
| Is the answer reasonable? | |
| Yes, $100 would be 1,254 pesos. $325 is a little more than 3 times this amount, so our answer of 4075.5 pesos makes sense. | |
 |
|
| Write a complete sentence. | Josiah got 4075.5 pesos for his spring break trip. |
Yurianna is going to Europe and wants to change $800 dollars into Euros. At the current exchange rate, $1 US is equal to 0.738 Euro. How many Euros will she have for her trip?
- Answer
-
590.4 Euros
Corey and Nicole are traveling to Japan and need to exchange $600 into Japanese yen. If each dollar is 94.1 yen, how many yen will they get?
- Answer
-
56,460 yen
In the example above, we related the number of pesos to the number of dollars by using a proportion. We could say the number of pesos is proportional to the number of dollars. If two quantities are related by a proportion, we say that they are proportional.
Solve Similar Figure Applications
When you shrink or enlarge a photo on a phone or tablet, figure out a distance on a map, or use a pattern to build a bookcase or sew a dress, you are working with similar figures. If two figures have exactly the same shape, but different sizes, they are said to be similar. One is a scale model of the other. All their corresponding angles have the same measures and their corresponding sides are in the same ratio.
Two figures are similar if the measures of their corresponding angles are equal and their corresponding sides are in the same ratio.
For example, the two triangles in the figure below are similar. Each side of ΔABC is 4 times the length of the corresponding side of ΔXYZ.
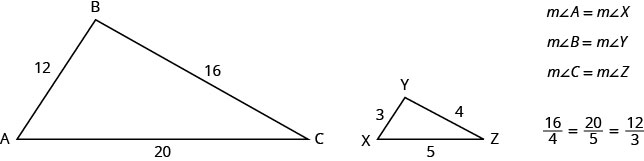
This is summed up in the Property of Similar Triangles.
If ΔABC is similar to ΔXYZ
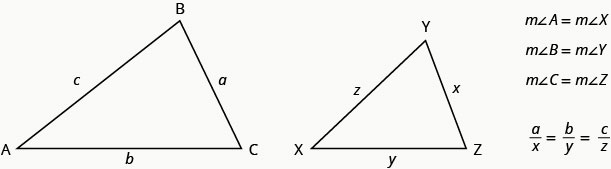
To solve applications with similar figures we will follow the Problem-Solving Strategy for Geometry Applications we used earlier.
- Read the problem and make all the words and ideas are understood. Draw the figure and label it with the given information.
- Identify what we are looking for.
- Name what we are looking for by choosing a variable to represent it.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
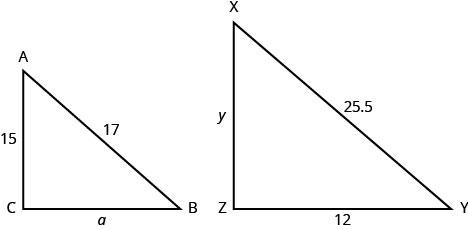
ΔABC is similar to ΔXYZ. The lengths of two sides of each triangle are given in the figure.
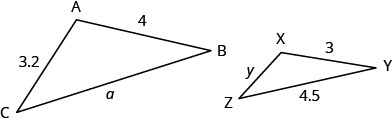
Find the length of the sides of the similar triangles.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | Figure is given. |
| Step 2. Identify what we are looking for. | the length of the sides of similar triangles. |
| Step 3. Name the variables. |
Let a= length of the third side of ΔABC. y= length of the third side of ΔXYZ. |
| Step 4. Translate. | Since the triangles are similar, the corresponding sides are proportional. |
| We need to write an equation that compares the side we are looking for to a known ratio. Since the side AB = 4 corresponds to the side XY = 3 we know ABXY=43. So we write equations with ABXY to find the sides we are looking for. Be careful to match up corresponding sides correctly. | ABXY=BCYZ=ACXZ. |
| Substitute. | 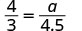 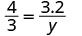 |
| Step 5. Solve the equation. |
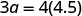
|
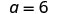 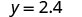 |
|
| Step 6. Check. | |
| Step 7. Answer the question. | The third side of ΔABC is 6 and the third side of ΔXYZ is 2.4. |
ΔABC is similar to ΔXYZ. The lengths of two sides of each triangle are given in the figure.
Find the length of side a
- Answer
-
8
ΔABC is similar to ΔXYZ. The lengths of two sides of each triangle are given in the figure.
- Answer
-
22.5
The next example shows how similar triangles are used with maps.
On a map, San Francisco, Las Vegas, and Los Angeles form a triangle whose sides are shown in the figure below. If the actual distance from Los Angeles to Las Vegas is 270 miles find the distance from Los Angeles to San Francisco.
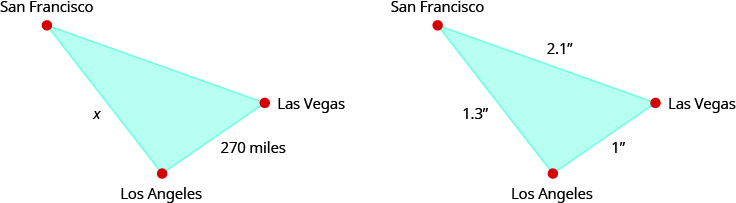
Solution
| Read the problem. Draw the figures and label with the given information. | The figures are shown above. |
| Identify what we are looking for. | The actual distance from Los Angeles to San Francisco. |
| Name the variables. | Let x= distance from Los Angeles to San Francisco. |
| Translate into an equation. Since the triangles are similar, the corresponding sides are proportional. We'll make the numerators "miles" and the denominators "inches." |
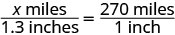 |
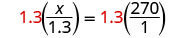 |
|
| Solve the equation. | 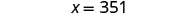 |
| Check. | |
| On the map, the distance from Los Angeles to San Francisco is more than the distance from Los Angeles to Las Vegas. Since 351 is more than 270 the answer makes sense. |
|
 |
|
| Answer the question. | The distance from Los Angeles to San Francisco is 351 miles. |
On the map, Seattle, Portland, and Boise form a triangle whose sides are shown in the figure below. If the actual distance from Seattle to Boise is 400 miles, find the distance from Seattle to Portland.
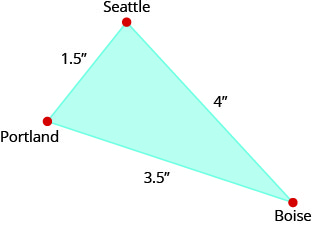
- Answer
-
150 miles
Using the map above, find the distance from Portland to Boise.
- Answer
-
350 miles
We can use similar figures to find heights that we cannot directly measure.
Tyler is 6 feet tall. Late one afternoon, his shadow was 8 feet long. At the same time, the shadow of a tree was 24 feet long. Find the height of the tree.
Solution
| Read the problem and draw a figure. | 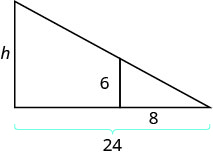 |
| We are looking for h, the height of the tree. | |
| We will use similar triangles to write an equation. | |
| The small triangle is similar to the large triangle. | 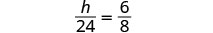 |
| Solve the proportion. | 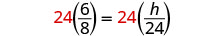 |
| Simplify. | 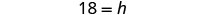 |
| Check. | |
|
Tyler's height is less than his shadow's length so it makes sense that the tree's height is less than the length of its shadow. |
|
 |
A telephone pole casts a shadow that is 50 feet long. Nearby, an 8 foot tall traffic sign casts a shadow that is 10 feet long. How tall is the telephone pole?
- Answer
-
40 feet
A pine tree casts a shadow of 80 feet next to a 30-foot tall building which casts a 40 feet shadow. How tall is the pine tree?
- Answer
-
60 feet
Key Concepts
- Property of Similar Triangles
- If ΔABC is similar to ΔXYZ
- Problem Solving Strategy for Geometry Applications
- Read the problem and make sure all the words and ideas are understood. Draw the figure and label it with the given information.
- Identify what we are looking for.
- Name what we are looking for by choosing a variable to represent it.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Glossary
- proportion
- A proportion is an equation of the form ab=cd,where\(b≠0, d≠0. The proportion is read “a is to b c is to d."
- similar figures
- Two figures are similar if the measures of their corresponding angles are equal and their corresponding sides are in the same ratio.