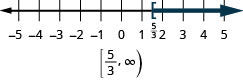Chapter 2 Review Exercises
- Last updated
- Jan 7, 2020
- Save as PDF
- Page ID
- 30487
( \newcommand{\kernel}{\mathrm{null}\,}\)
Chapter 2 Review Exercises
Solve Equations using the Subtraction and Addition Properties of Equality
Verify a Solution of an Equation
In the following exercises, determine whether each number is a solution to the equation.
Exercise \PageIndex{1}
10 x-1=5 x ; x=\frac{1}{5}
Exercise \PageIndex{2}
w+2=\frac{5}{8} ; w=\frac{3}{8}
- Answer
-
no
Exercise \PageIndex{3}
-12 n+5=8 n ; n=-\frac{5}{4}
Exercise \PageIndex{4}
6 a-3=-7 a, a=\frac{3}{13}
- Answer
-
yes
Solve Equations using the Subtraction and Addition Properties of Equality
In the following exercises, solve each equation using the Subtraction Property of Equality.
Exercise \PageIndex{5}
x+7=19
Exercise \PageIndex{6}
y+2=-6
- Answer
-
y=-8
Exercise \PageIndex{7}
a+\frac{1}{3}=\frac{5}{3}
Exercise \PageIndex{8}
n+3.6=5.1
- Answer
-
n=1.5
In the following exercises, solve each equation using the Addition Property of Equality.
Exercise \PageIndex{9}
u-7=10
Exercise \PageIndex{10}
x-9=-4
- Answer
-
x=5
Exercise \PageIndex{11}
c-\frac{3}{11}=\frac{9}{11}
Exercise \PageIndex{12}
p-4.8=14
- Answer
-
p=18.8
In the following exercises, solve each equation.
Exercise \PageIndex{13}
n-12=32
Exercise \PageIndex{14}
y+16=-9
- Answer
-
y=-25
Exercise \PageIndex{15}
f+\frac{2}{3}=4
Exercise \PageIndex{16}
d-3.9=8.2
- Answer
-
d=12.1
Solve Equations That Require Simplification
In the following exercises, solve each equation.
Exercise \PageIndex{17}
y+8-15=-3
Exercise \PageIndex{18}
7 x+10-6 x+3=5
- Answer
-
x=-8
Exercise \PageIndex{19}
6(n-1)-5 n=-14
Exercise \PageIndex{20}
8(3 p+5)-23(p-1)=35
- Answer
-
p=-28
Translate to an Equation and Solve
In the following exercises, translate each English sentence into an algebraic equation and then solve it.
Exercise \PageIndex{21}
The sum of -6 and m is 25
Exercise \PageIndex{22}
Four less than n is 13
- Answer
-
n-4=13 ; n=17
Translate and Solve Applications
In the following exercises, translate into an algebraic equation and solve.
Exercise \PageIndex{23}
Rochelle’s daughter is 11 years old. Her son is 3 years younger. How old is her son?
Exercise \PageIndex{24}
Tan weighs 146 pounds. Minh weighs 15 pounds more than Tan. How much does Minh weigh?
- Answer
-
161 pounds
Exercise \PageIndex{25}
Peter paid $9.75 to go to the movies, which was $46.25 less than he paid to go to a concert. How much did he pay for the concert?
Exercise \PageIndex{26}
Elissa earned \$ 152.84 this week, which was \$ 2 . .65 more than she earned last week. How much did she earn last week?
- Answer
-
\$ 131.19
Solve Equations using the Division and Multiplication Properties of Equality
Solve Equations Using the Division and Multiplication Properties of Equality
In the following exercises, solve each equation using the division and multiplication properties of equality and check the solution.
Exercise \PageIndex{27}
8 x=72
Exercise \PageIndex{28}
13 a=-65
- Answer
-
a=-5
Exercise \PageIndex{29}
0.25 p=5.25
Exercise \PageIndex{30}
-y=4
- Answer
-
y=-4
Exercise \PageIndex{31}
\frac{n}{6}=18
Exercise \PageIndex{32}
\frac{y}{-10}=30
- Answer
-
y=-300
Exercise \PageIndex{33}
36=\frac{3}{4} x
Exercise \PageIndex{34}
\frac{5}{8} u=\frac{15}{16}
- Answer
-
u=\frac{3}{2}
Exercise \PageIndex{35}
-18 m=-72
Exercise \PageIndex{36}
\frac{c}{9}=36
- Answer
-
c=324
Exercise \PageIndex{37}
0.45 x=6.75
Exercise \PageIndex{38}
\frac{11}{12}=\frac{2}{3} y
- Answer
-
y=\frac{11}{8}
Solve Equations That Require Simplification
In the following exercises, solve each equation requiring simplification.
Exercise \PageIndex{39}
5 r-3 r+9 r=35-2
Exercise \PageIndex{40}
24 x+8 x-11 x=-7-14
- Answer
-
x=-1
Exercise \PageIndex{41}
\frac{11}{12} n-\frac{5}{6} n=9-5
Exercise \PageIndex{42}
-9(d-2)-15=-24
- Answer
-
d=3
Translate to an Equation and Solve
In the following exercises, translate to an equation and then solve.
Exercise \PageIndex{43}
143 is the product of -11 and y
Exercise \PageIndex{44}
The quotient of b and and 9 is -27
- Answer
-
\frac{b}{9}=-27 ; b=-243
Exercise \PageIndex{45}
The sum of q and one-fourth is one.
Exercise \PageIndex{46}
The difference of s and one-twelfth is one fourth.
- Answer
-
s-\frac{1}{12}=\frac{1}{4} ; s=\frac{1}{3}
Translate and Solve Applications
In the following exercises, translate into an equation and solve.
Exercise \PageIndex{47}
Ray paid $21 for 12 tickets at the county fair. What was the price of each ticket?
Exercise \PageIndex{48}
Janet gets paid \$ 24 per hour. She heard that this is \frac{3}{4} of what Adam is paid. How much is Adam paid per hour?
- Answer
-
$32
Solve Equations with Variables and Constants on Both Sides
Solve an Equation with Constants on Both Sides
In the following exercises, solve the following equations with constants on both sides.
Exercise \PageIndex{49}
8 p+7=47
Exercise \PageIndex{50}
10 w-5=65
- Answer
-
w=7
Exercise \PageIndex{51}
3 x+19=-47
Exercise \PageIndex{52}
32=-4-9 n
- Answer
-
n=-4
Solve an Equation with Variables on Both Sides
In the following exercises, solve the following equations with variables on both sides.
Exercise \PageIndex{53}
7 y=6 y-13
Exercise \PageIndex{54}
5 a+21=2 a
- Answer
-
a=-7
Exercise \PageIndex{55}
k=-6 k-35
Exercise \PageIndex{56}
4 x-\frac{3}{8}=3 x
- Answer
-
x=\frac{3}{8}
Solve an Equation with Variables and Constants on Both Sides
In the following exercises, solve the following equations with variables and constants on both sides.
Exercise \PageIndex{57}
12 x-9=3 x+45
Exercise \PageIndex{58}
5 n-20=-7 n-80
- Answer
-
n=-5
Exercise \PageIndex{59}
4 u+16=-19-u
Exercise \PageIndex{60}
\frac{5}{8} c-4=\frac{3}{8} c+4
- Answer
-
c=32
Use a General Strategy for Solving Linear Equations
Solve Equations Using the General Strategy for Solving Linear Equations
In the following exercises, solve each linear equation.
Exercise \PageIndex{61}
6(x+6)=24
Exercise \PageIndex{62}
9(2 p-5)=72
- Answer
-
p=\frac{13}{2}
Exercise \PageIndex{63}
-(s+4)=18
Exercise \PageIndex{64}
8+3(n-9)=17
- Answer
-
n=12
Exercise \PageIndex{65}
23-3(y-7)=8
Exercise \PageIndex{66}
\frac{1}{3}(6 m+21)=m-7
- Answer
-
m=-14
Exercise \PageIndex{67}
4(3.5 y+0.25)=365
Exercise \PageIndex{68}
0.25(q-8)=0.1(q+7)
- Answer
-
q=18
Exercise \PageIndex{69}
8(r-2)=6(r+10)
Exercise \PageIndex{70}
\begin{array}{l}{5+7(2-5 x)=2(9 x+1)} \\ {-(13 x-57)}\end{array}
- Answer
-
x=-1
Exercise \PageIndex{71}
\begin{array}{l}{(9 n+5)-(3 n-7)} \\ {=20-(4 n-2)}\end{array}
Exercise \PageIndex{72}
\begin{array}{l}{2[-16+5(8 k-6)]} \\ {=8(3-4 k)-32}\end{array}
- Answer
-
k=\frac{3}{4}
Classify Equations
In the following exercises, classify each equation as a conditional equation, an identity, or a contradiction and then state the solution.
Exercise \PageIndex{73}
\begin{array}{l}{17 y-3(4-2 y)=11(y-1)} \\ {+12 y-1}\end{array}
Exercise \PageIndex{74}
\begin{array}{l}{9 u+32=15(u-4)} \\ {-3(2 u+21)}\end{array}
- Answer
-
contradiction; no solution
Exercise \PageIndex{75}
-8(7 m+4)=-6(8 m+9)
Exercise \PageIndex{76}
\begin{array}{l}{21(c-1)-19(c+1)} \\ {=2(c-20)}\end{array}
- Answer
-
identity; all real numbers
Solve Equations with Fractions and Decimals
Solve Equations with Fraction Coefficients
In the following exercises, solve each equation with fraction coefficients.
Exercise \PageIndex{77}
\frac{2}{5} n-\frac{1}{10}=\frac{7}{10}
Exercise \PageIndex{78}
\frac{1}{3} x+\frac{1}{5} x=8
- Answer
-
x=15
Exercise \PageIndex{79}
\frac{3}{4} a-\frac{1}{3}=\frac{1}{2} a-\frac{5}{6}
Exercise \PageIndex{80}
\frac{1}{2}(k-3)=\frac{1}{3}(k+16)
- Answer
-
k=41
Exercise \PageIndex{81}
\frac{3 x-2}{5}=\frac{3 x+4}{8}
Exercise \PageIndex{82}
\frac{5 y-1}{3}+4=\frac{-8 y+4}{6}
- Answer
-
y=-1
Solve Equations with Decimal Coefficients
In the following exercises, solve each equation with decimal coefficients.
Exercise \PageIndex{83}
0.8 x-0.3=0.7 x+0.2
Exercise \PageIndex{84}
0.36 u+2.55=0.41 u+6.8
- Answer
-
u=-85
Exercise \PageIndex{85}
0.6 p-1.9=0.78 p+1.7
Exercise \PageIndex{86}
0.6 p-1.9=0.78 p+1.7
- Answer
-
d=-20
Solve a Formula for a Specific Variable
Use the Distance, Rate, and Time Formula
In the following exercises, solve.
Exercise \PageIndex{87}
Natalie drove for 7\frac{1}{2} hours at 60 miles per hour. How much distance did she travel?
Exercise \PageIndex{88}
Mallory is taking the bus from St. Louis to Chicago. The distance is 300 miles and the bus travels at a steady rate of 60 miles per hour. How long will the bus ride be?
- Answer
-
5 hours
Exercise \PageIndex{89}
Aaron’s friend drove him from Buffalo to Cleveland. The distance is 187 miles and the trip took 2.75 hours. How fast was Aaron’s friend driving?
Exercise \PageIndex{90}
Link rode his bike at a steady rate of 15 miles per hour for 2\frac{1}{2} hours. How much distance did he travel?
- Answer
-
37.5 miles
Solve a Formula for a Specific Variable
In the following exercises, solve.
Exercise \PageIndex{91}
Use the formula. d=rt to solve for t
- when d=510 and r=60
- in general
Exercise \PageIndex{92}
Use the formula. d=rt to solve for r
- when when d=451 and t=5.5
- in general
- Answer
-
- r=82mph
- r=\frac{D}{t}
Exercise \PageIndex{93}
Use the formula A=\frac{1}{2} b h to solve for b
- when A=390 and h=26
- in general
Exercise \PageIndex{94}
Use the formula A=\frac{1}{2} b h to solve for b
- when A=153 and b=18
- in general
- Answer
-
- h=17
- h=\frac{2 A}{b}
Exercise \PageIndex{95}
Use the formula I=Prt to solve for the principal, P for
- I=$2,501,r=4.1%, t=5 years
- in general
Exercise \PageIndex{96}
Solve the formula 4x+3y=6 for y
- when x=−2
- in general
- Answer
-
ⓐ y=\frac{14}{3} ⓑ y=\frac{6-4 x}{3}
Exercise \PageIndex{97}
Solve 180=a+b+c for c
Exercise \PageIndex{98}
Solve the formula V=L W H for H
- Answer
-
H=\frac{V}{L W}
Solve Linear Inequalities
Graph Inequalities on the Number Line
In the following exercises, graph each inequality on the number line.
Exercise \PageIndex{99}
- x\leq 4
- x>−2
- x<1
Exercise \PageIndex{100}
- x>0
- x<−3
- x\geq −1
- Answer
-
In the following exercises, graph each inequality on the number line and write in interval notation.
Exercise \PageIndex{101}
- x<-1
- x \geq-2.5
- x \leq \frac{5}{4}
Exercise \PageIndex{102}
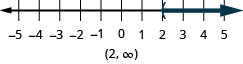
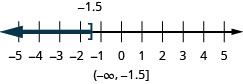
- x>2
- x \leq-1.5
- x \geq \frac{5}{3}
- Answer
-
Solve Inequalities using the Subtraction and Addition Properties of Inequality
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
Exercise \PageIndex{103}
n-12 \leq 23
Exercise \PageIndex{104}
m+14 \leq 56
- Answer
-
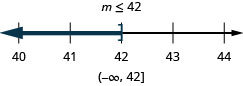
Exercise \PageIndex{105}
a+\frac{2}{3} \geq \frac{7}{12}
Exercise \PageIndex{106}
b-\frac{7}{8} \geq-\frac{1}{2}
- Answer
-
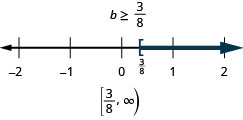
Solve Inequalities using the Division and Multiplication Properties of Inequality
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
Exercise \PageIndex{107}
9 x>54
Exercise \PageIndex{108}
-12 d \leq 108
- Answer
-
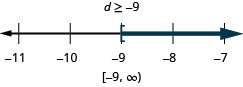
Exercise \PageIndex{109}
\frac{5}{2} j<-60
Exercise \PageIndex{110}
\frac{q}{-2} \geq-24
- Answer
-
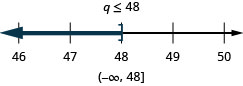
Solve Inequalities That Require Simplification
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
Exercise \PageIndex{111}
6 p>15 p-30
Exercise \PageIndex{112}
9 h-7(h-1) \leq 4 h-23
- Answer
-
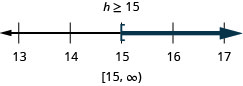
Exercise \PageIndex{113}
5 n-15(4-n)<10(n-6)+10 n
Exercise \PageIndex{114}
\frac{3}{8} a-\frac{1}{12} a>\frac{5}{12} a+\frac{3}{4}
- Answer
-
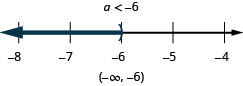
Translate to an Inequality and Solve
In the following exercises, translate and solve. Then write the solution in interval notation and graph on the number line.
Exercise \PageIndex{115}
Five more than z is at most 19.
Exercise \PageIndex{116}
Three less than c is at least 360.
- Answer
-
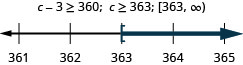
Exercise \PageIndex{117}
Nine times n exceeds 42.
Exercise \PageIndex{118}
Negative two times a is no more than 8.
- Answer
-
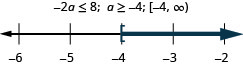
Everyday Math
Exercise \PageIndex{119}
Describe how you have used two topics from this chapter in your life outside of your math class during the past month.
Chapter 2 Practice Test
Exercise \PageIndex{1}
Determine whether each number is a solution to the equation 6 x-3=x+20
- 5
- \frac{23}{5}
- Answer
-
- no
- yes
In the following exercises, solve each equation.
Exercise \PageIndex{2}
n-\frac{2}{3}=\frac{1}{4}
Exercise \PageIndex{3}
\frac{9}{2} c=144
- Answer
-
c=32
Exercise \PageIndex{4}
4 y-8=16
Exercise \PageIndex{5}
-8 x-15+9 x-1=-21
- Answer
-
x=-5
Exercise \PageIndex{6}
-15 a=120
Exercise \PageIndex{7}
\frac{2}{3} x=6
- Answer
-
x=9
Exercise \PageIndex{8}
x-3.8=8.2
Exercise \PageIndex{9}
10 y=-5 y-60
- Answer
-
y=-4
Exercise \PageIndex{10}
8 n-2=6 n-12
Exercise \PageIndex{11}
9 m-2-4 m-m=42-8
- Answer
-
m=9
Exercise \PageIndex{12}
-5(2 x-1)=45
Exercise \PageIndex{13}
-(d-9)=23
- Answer
-
d=-14
Exercise \PageIndex{14}
\frac{1}{4}(12 m-28)=6-2(3 m-1)
Exercise \PageIndex{15}
2(6 x-5)-8=-22
- Answer
-
x=-\frac{1}{3}
Exercise \PageIndex{16}
8(3 a-5)-7(4 a-3)=20-3 a
Exercise \PageIndex{17}
\frac{1}{4} p-\frac{1}{3}=\frac{1}{2}
- Answer
-
p=\frac{10}{3}
Exercise \PageIndex{18}
0.1 d+0.25(d+8)=4.1
Exercise \PageIndex{19}
14 n-3(4 n+5)=-9+2(n-8)
- Answer
-
contradiction; no solution
Exercise \PageIndex{20}
9(3 u-2)-4[6-8(u-1)]=3(u-2)
Exercise \PageIndex{21}
Solve the formula x−2y=5 for y
- when x=−3
- in general
- Answer
-
- y=4
- y=\frac{5-x}{2}
In the following exercises, graph on the number line and write in interval notation.
Exercise \PageIndex{22}
x \geq-3.5
Exercise \PageIndex{23}
x<\frac{11}{4}
- Answer
-
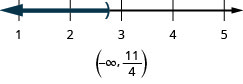
In the following exercises,, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
Exercise \PageIndex{24}
8 k \geq 5 k-120
Exercise \PageIndex{25}
3 c-10(c-2)<5 c+16
- Answer
-
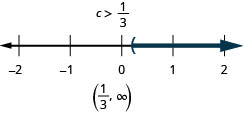
In the following exercises, translate to an equation or inequality and solve.
Exercise \PageIndex{26}
4 less than twice x is 16.
Exercise \PageIndex{27}
Fifteen more than n is at least 48.
- Answer
-
n+15 \geq 48 ; n \geq 33
Exercise \PageIndex{28}
Samuel paid $25.82 for gas this week, which was $3.47 less than he paid last week. How much had he paid last week?
Exercise \PageIndex{29}
Jenna bought a coat on sale for \$ 120, which was \frac{2}{3} of the original price. What was the original price of the coat?
- Answer
-
120=\frac{2}{3} p ; The original price was \$ 180
Exercise \PageIndex{30}
Sean took the bus from Seattle to Boise, a distance of 506 miles. If the trip took 7\frac{2}{3} hours, what was the speed of the bus?
Review for 2.7 Ratio and Proportions and Similar Triangles
Solve Proportions
In the following exercises, solve.
Exercise \PageIndex{74}
\dfrac{x}{4}=\dfrac{3}{5}
- Answer
-
\dfrac{12}{5}
Exercise \PageIndex{75}
\dfrac{3}{y}=\dfrac{9}{5}
Exercise \PageIndex{76}
\dfrac{s}{s+20}=\dfrac{3}{7}
- Answer
-
15
Exercise \PageIndex{77}
\dfrac{t−3}{5}=\dfrac{t+2}{9}
In the following exercises, solve using proportions.
Exercise \PageIndex{78}
Rachael had a 21 ounce strawberry shake that has 739 calories. How many calories are there in a 32 ounce shake?
- Answer
-
1161 calories
Exercise \PageIndex{79}
Leo went to Mexico over Christmas break and changed $525 dollars into Mexican pesos. At that time, the exchange rate had $1 US is equal to 16.25 Mexican pesos. How many Mexican pesos did he get for his trip?
In the following exercises, solve.
Exercise \PageIndex{80}
∆ABC is similar to ∆XYZ. The lengths of two sides of each triangle are given in the figure. Find the lengths of the third sides.
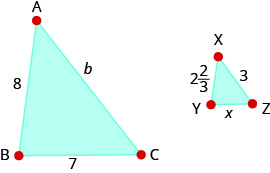
- Answer
-
b=9; x=2\dfrac{1}{3}
Exercise \PageIndex{81}
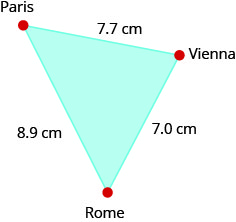
On a map of Europe, Paris, Rome, and Vienna form a triangle whose sides are shown in the figure below. If the actual distance from Rome to Vienna is 700 miles, find the distance from
- a. Paris to Rome
- b. Paris to Vienna
Exercise \PageIndex{82}
Tony is 5.75 feet tall. Late one afternoon, his shadow was 8 feet long. At the same time, the shadow of a nearby tree was 32 feet long. Find the height of the tree.
- Answer
-
23 feet
Exercise \PageIndex{83}
The height of a lighthouse in Pensacola, Florida is 150 feet. Standing next to the statue, 5.5 foot tall Natalie cast a 1.1 foot shadow How long would the shadow of the lighthouse be?
Review for 2.9 Compound Inequalities
Solve Compound Inequalities with “and”
In each of the following exercises, solve each inequality, graph the solution, and write the solution in interval notation.
98. x\leq 5 and x>−3
- Answer
-
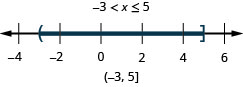
99. 4x−2\leq 4 and 7x−1>−8
100. 5(3x−2)\leq 5 and 4(x+2)<3
- Answer
-
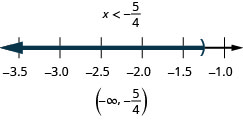
101. 34(x−8)\leq 3 and 15(x−5)\leq 3
102. 34x−5\geq −2 and −3(x+1)\geq 6
- Answer
-
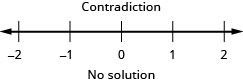
103. −5\leq 4x−1<7
Solve Compound Inequalities with “or”
In the following exercises, solve each inequality, graph the solution on the number line, and write the solution in interval notation.
104. 5−2x\leq −1 or 6+3x\leq 4
- Answer
-
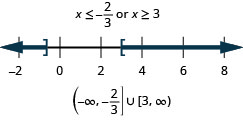
105. 3(2x−3)<−5 or 4x−1>3
106. 34x−2>4 or 4(2−x)>0
- Answer
-
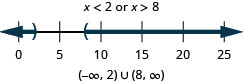
107. 2(x+3)\geq 0 or 3(x+4)\leq 6
108. 12x−3\leq 4 or 13(x−6)\geq −2
- Answer
-
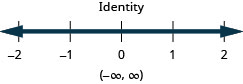
Solve Applications with Compound Inequalities
In the following exercises, solve.
109. Liam is playing a number game with his sister Audry. Liam is thinking of a number and wants Audry to guess it. Five more than three times her number is between 2 and 32. Write a compound inequality that shows the range of numbers that Liam might be thinking of.
110. Elouise is creating a rectangular garden in her back yard. The length of the garden is 12 feet. The perimeter of the garden must be at least 36 feet and no more than 48 feet. Use a compound inequality to find the range of values for the width of the garden.
- Answer
-
6\leq w\leq 12