3.4: Solve Mixture Applications
- Last updated
- Save as PDF
- Page ID
- 30493
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
By the end of this section, you will be able to:
- Solve coin word problems
- Solve ticket and stamp word problems
- Solve mixture word problems
- Use the mixture model to solve investment problems using simple interest
Note
Before you get started, take this readiness quiz.
- Multiply: \(14(0.25)\).
If you missed this problem, review Exercise 1.8.19. - Solve: \(0.25x+0.10(x+4)=2.5\).
If you missed this problem, review Exercise 2.4.22. - The number of dimes is three more than the number of quarters. Let q represent the number of quarters. Write an expression for the number of dimes.
If you missed this problem, review Exercise 1.3.43.
Solve Coin Word Problems
In mixture problems, we will have two or more items with different values to combine together. The mixture model is used by grocers and bartenders to make sure they set fair prices for the products they sell. Many other professionals, like chemists, investment bankers, and landscapers also use the mixture model.
Note
Doing the Manipulative Mathematics activity Coin Lab will help you develop a better understanding of mixture word problems.
We will start by looking at an application everyone is familiar with—money!
Imagine that we take a handful of coins from a pocket or purse and place them on a desk. How would we determine the value of that pile of coins? If we can form a step-by-step plan for finding the total value of the coins, it will help us as we begin solving coin word problems.
So what would we do? To get some order to the mess of coins, we could separate the coins into piles according to their value. Quarters would go with quarters, dimes with dimes, nickels with nickels, and so on. To get the total value of all the coins, we would add the total value of each pile.

How would we determine the value of each pile? Think about the dime pile—how much is it worth? If we count the number of dimes, we’ll know how many we have—the number of dimes.
But this does not tell us the value of all the dimes. Say we counted 17 dimes, how much are they worth? Each dime is worth $0.10—that is the value of one dime. To find the total value of the pile of 17 dimes, multiply 17 by $0.10 to get $1.70. This is the total value of all 17 dimes. This method leads to the following model.
TOTAL VALUE OF COINS
For the same type of coin, the total value of a number of coins is found by using the model
\[number\cdot value = total\space value\]
where
number is the number of coins
value is the value of each coin
total value is the total value of all the coins
The number of dimes times the value of each dime equals the total value of the dimes.
\[\begin{aligned} \text {number.} \cdot \text { value } &=\text { total value } \\ 17 \cdot \$ 0.10 &=\$ 1.70 \end{aligned}\]
We could continue this process for each type of coin, and then we would know the total value of each type of coin. To get the total value of all the coins, add the total value of each type of coin.
Let’s look at a specific case. Suppose there are 14 quarters, 17 dimes, 21 nickels, and 39 pennies.
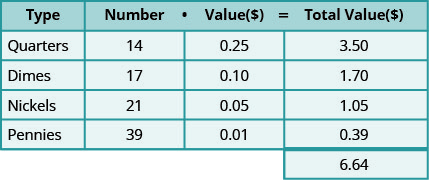
Table \(\PageIndex{1}\)
The total value of all the coins is $6.64.
Notice how the chart helps organize all the information! Let’s see how we use this method to solve a coin word problem.
Example \(\PageIndex{1}\)
Adalberto has $2.25 in dimes and nickels in his pocket. He has nine more nickels than dimes. How many of each type of coin does he have?
Solution
Step 1. Read the problem. Make sure all the words and ideas are understood.
Determine the types of coins involved.Think about the strategy we used to find the value of the handful of coins. The first thing we need is to notice what types of coins are involved. Adalberto has dimes and nickels. Create a table to organize the information. See chart below.
- Label the columns “type,” “number,” “value,” “total value.”
- List the types of coins.
- Write in the value of each type of coin.
- Write in the total value of all the coins.
The value of a dime is $0.10 and the value of a nickel is $0.05. The total value of all the coins is $2.25. The table below shows this information.
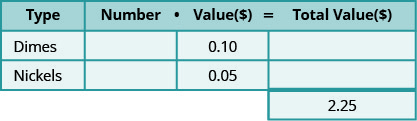
-
Step 2. Identify what we are looking for.
We are asked to find the number of dimes and nickels Adalberto has.
Step 3. Name what we are looking for. Choose a variable to represent that quantity.
Use variable expressions to represent the number of each type of coin and write them in the table. -
Multiply the number times the value to get the total value of each type of coin.
Next we counted the number of each type of coin. In this problem we cannot count each type of coin—that is what you are looking for—but we have a clue. There are nine more nickels than dimes. The number of nickels is nine more than the number of dimes.
\[\begin{aligned} \text { Let } d &=\text { number of dimes. } \\ d+9 &=\text { number of nickels } \end{aligned}\]
Fill in the “number” column in the table to help get everything organized.
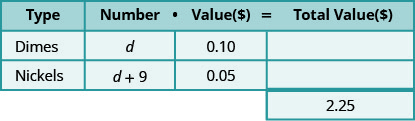
Now we have all the information we need from the problem!
We multiply the number times the value to get the total value of each type of coin. While we do not know the actual number, we do have an expression to represent it.
And so now multiply \(\text{number}\cdot\text{value}=\text{total value}\). See how this is done in the table below.
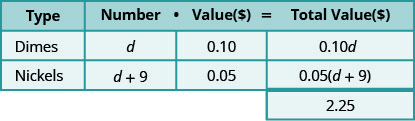
Notice that we made the heading of the table show the model.
Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence. Translate the English sentence into an algebraic equation.
Write the equation by adding the total values of all the types of coins.
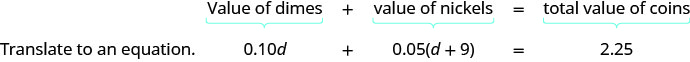
Step 5. Solve the equation using good algebra techniques.
Now solve this equation. 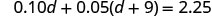
Distribute. 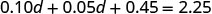
Combine like terms. 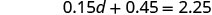
Subtract 0.45 from each side. 
Divide. 
So there are 12 dimes. The number of nickels is d+9d+9. 

21 Step 6. Check the answer in the problem and make sure it makes sense.
Does this check?
\[\begin{array}{llll}{12 \text { dimes }} & {12(0.10)} &{=} &{1.20} \\ {21 \text { nickels }} & {21(0.05)} & {=} &{\underline{1.05}} \\ {} &{} &{}&{$ 2.25\checkmark} \end{array}\]
Step 7. Answer the question with a complete sentence.
Adalberto has twelve dimes and twenty-one nickels.
If this were a homework exercise, our work might look like the following.

Try It \(\PageIndex{1}\)
Michaela has $2.05 in dimes and nickels in her change purse. She has seven more dimes than nickels. How many coins of each type does she have?
- Answer
-
9 nickels, 16 dimes
Try It \(\PageIndex{2}\)
Liliana has $2.10 in nickels and quarters in her backpack. She has 12 more nickels than quarters. How many coins of each type does she have?
- Answer
-
17 nickels, 5 quarters
SOLVE COIN WORD PROBLEMS.
- Read the problem. Make sure all the words and ideas are understood.
- Determine the types of coins involved.
- Create a table to organize the information.
- Label the columns “type,” “number,” “value,” “total value.”
- List the types of coins.
- Write in the value of each type of coin.
- Write in the total value of all the coins.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Use variable expressions to represent the number of each type of coin and write them in the table.
- Multiply the number times the value to get the total value of each type of coin.
- Translate into an equation.
It may be helpful to restate the problem in one sentence with all the important information. Then, translate the sentence into an equation.
Write the equation by adding the total values of all the types of coins. - Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Example \(\PageIndex{2}\)
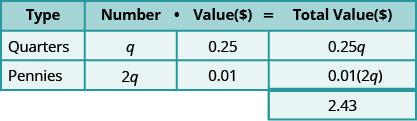
Maria has $2.43 in quarters and pennies in her wallet. She has twice as many pennies as quarters. How many coins of each type does she have?
Solution
Step 1. Read the problem.
Determine the types of coins involved.
We know that Maria has quarters and pennies.
Create a table to organize the information.
- Step 2. Identify what you are looking for.
- We are looking for the number of quarters and pennies.
Step 3. Name. Represent the number of quarters and pennies using variables.
- Multiply the ‘number’ and the ‘value’ to get the ‘total value’ of each type of coin.
Step 4. Translate. Write the equation by adding the ‘total value’ of all the types of coins.
\(\begin{array} {ll} {\textbf{Step5. Solve} \text{ the equation.}} &{0.25q + 0.01(2q) = 2.43} \\{\text{Multiply.}} &{0.25q + 0.02q = 2.43} \\ {\text{Combine like terms.}} &{0.27q = 2.43} \\ {\text{Divide by 0.27}} &{q = 9 \text{ quarters}} \\ {\text{The number of pennies is 2q.}} &{2q} \\ {} &{2\cdot 9} \\ {} &{18 \text{ pennies}} \\ {\textbf{Step 6. Check} \text{ the answer in the problem.}} &{} \\\\ {\text{Maria has 9 quarters and 18 pennies. Dies this}} &{} \\ {\text{make }$2.43?} &{} \end{array}\)
\(\begin{array} {llll}\\ {9\text{ quarters }} &{ 9(0.25)} &{=} &{2.25} \\ {18\text{ pennies }} &{18(0.01)} &{=} &{\underline{0.18}} &{}\\ {\text{Total}} &{} &{} &{$2.43\checkmark} \end{array}\)
\(\begin{array} {ll} \\ {\textbf{Step 7. Answer}\text{ the question.}} &{\text{Maria has nine quarters and eighteen pennies.}} \end{array}\)
Try It \(\PageIndex{3}\)
Sumanta has $4.20 in nickels and dimes in her piggy bank. She has twice as many nickels as dimes. How many coins of each type does she have?
- Answer
-
42 nickels, 21 dimes
Try It \(\PageIndex{4}\)
Alison has three times as many dimes as quarters in her purse. She has $9.35 altogether. How many coins of each type does she have?
- Answer
-
51 dimes, 17 quarters
In the next example, we’ll show only the completed table—remember the steps we take to fill in the table.
Example \(\PageIndex{3}\)
Danny has $2.14 worth of pennies and nickels in his piggy bank. The number of nickels is two more than ten times the number of pennies. How many nickels and how many pennies does Danny have?
Solution
| Step 1. Read the problem. | |
| Determine the types of coins involved. | pennies and nickels |
| Create a table. | |
| Write in the value of each type of coin. | Pennies are worth $0.01. Nickels are worth $0.05. |
| Step 2. Identify what we are looking for. | the number of pennies and nickels |
| Step 3. Name. Represent the number of each type of coin using variables. | |
| The number of nickels is defined in terms of the number of pennies, so start with pennies. | Let \(p=\) number of pennies. |
| The number of nickels is two more than ten times the number of pennies. | And let \(10p+2=\) number of nickels. |
| Multiply the number and the value to get the total value of each type of coin. | |
 |
|
| Step 4. Translate. Write the equation by adding the total value of all the types of coins. | 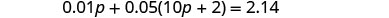 |
| Step 5. Solve the equation. | 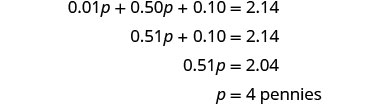 |
| How many nickels? |  |
| Step 6. Check the answer in the problem and make sure it makes sense Danny has four pennies and 42 nickels. Is the total value $2.14? \(\begin{array}{rll} {4(0.01)+42(0.05)} &{\stackrel{?}{=}} &{2.14} \\ {2.14} &{=} &{2.14\checkmark} \end{array}\) |
|
| Step 7. Answer the question. | Danny has four pennies and 42 nickels. |
Try It \(\PageIndex{5}\)
Jesse has $6.55 worth of quarters and nickels in his pocket. The number of nickels is five more than two times the number of quarters. How many nickels and how many quarters does Jesse have?
- Answer
-
41 nickels, 18 quarters
Try It \(\PageIndex{6}\)
Elane has $7.00 total in dimes and nickels in her coin jar. The number of dimes that Elane has is seven less than three times the number of nickels. How many of each coin does Elane have?
- Answer
-
22 nickels, 59 dimes
Solve Ticket and Stamp Word Problems
Problems involving tickets or stamps are very much like coin problems. Each type of ticket and stamp has a value, just like each type of coin does. So to solve these problems, we will follow the same steps we used to solve coin problems.
Example \(\PageIndex{4}\)
At a school concert, the total value of tickets sold was $1,506. Student tickets sold for $6 each and adult tickets sold for $9 each. The number of adult tickets sold was five less than three times the number of student tickets sold. How many student tickets and how many adult tickets were sold?
Solution
Step 1. Read the problem.
- Determine the types of tickets involved. There are student tickets and adult tickets.
- Create a table to organize the information.
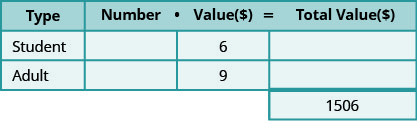
Step 2. Identify what we are looking for.
- We are looking for the number of student and adult tickets.
Step 3. Name. Represent the number of each type of ticket using variables.
We know the number of adult tickets sold was five less than three times the number of student tickets sold.
- Multiply the number times the value to get the total value of each type of ticket.
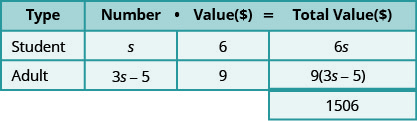
Step 4. Translate. Write the equation by adding the total values of each type of ticket.
\[6 s+9(3 s-5)=1506 \nonumber\]
Step 5. Solve the equation.
\[\begin{array}{rcl}{6 s+27 s-45} &{=} &{1506} \\ {33 s-45} &{=} &{1506} \\ {33 s} &{=} &{1551} \\ {s} & {=} &{47 \text { student tickets }} \\ {\text{Number of adult tickets}} &{=} &{3s-5} \\ {} &{=} &{3(47)-5} \\ {\text{So there were}} &{136} &{\text{adult tickets}}\end{array} \nonumber\]
Step 6. Check the answer.
There were 47 student tickets at $6 each and 136 adult tickets at $9 each. Is the total value $1,506? We find the total value of each type of ticket by multiplying the number of tickets times its value then add to get the total value of all the tickets sold.
\[\begin{array}{lll} {47\cdot 6} &{=} &{282} \\ {136\cdot 9} &{=} &{\underline{1224}} \\ {} &{} &{1506\checkmark} \\\end{array} \nonumber\]
Step 7. Answer the question. They sold 47 student tickets and 136 adult tickets.
Try It \(\PageIndex{7}\)
The first day of a water polo tournament the total value of tickets sold was $17,610. One-day passes sold for $20 and tournament passes sold for $30. The number of tournament passes sold was 37 more than the number of day passes sold. How many day passes and how many tournament passes were sold?
- Answer
-
330 day passes, 367 tournament passes
Try It \(\PageIndex{8}\)
At the movie theater, the total value of tickets sold was $2,612.50. Adult tickets sold for $10 each and senior/child tickets sold for $7.50 each. The number of senior/child tickets sold was 25 less than twice the number of adult tickets sold. How many senior/child tickets and how many adult tickets were sold?
- Answer
-
112 adult tickets, 199 senior/child tickets
We have learned how to find the total number of tickets when the number of one type of ticket is based on the number of the other type. Next, we’ll look at an example where we know the total number of tickets and have to figure out how the two types of tickets relate.
Suppose Bianca sold a total of 100 tickets. Each ticket was either an adult ticket or a child ticket. If she sold 20 child tickets, how many adult tickets did she sell?
- Did you say ‘80’? How did you figure that out? Did you subtract 20 from 100?
If she sold 45 child tickets, how many adult tickets did she sell?
- Did you say ‘55’? How did you find it? By subtracting 45 from 100?
What if she sold 75 child tickets? How many adult tickets did she sell?
- The number of adult tickets must be 100−75. She sold 25 adult tickets.
Now, suppose Bianca sold x child tickets. Then how many adult tickets did she sell? To find out, we would follow the same logic we used above. In each case, we subtracted the number of child tickets from 100 to get the number of adult tickets. We now do the same with x.
We have summarized this below.
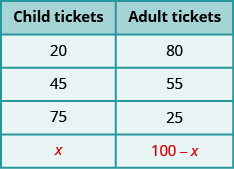
Table \(\PageIndex{2}\)
We can apply these techniques to other examples
Example \(\PageIndex{5}\)
Galen sold 810 tickets for his church’s carnival for a total of $2,820. Children’s tickets cost $3 each and adult tickets cost $5 each. How many children’s tickets and how many adult tickets did he sell?
Solution
Step 1. Read the problem.
- Determine the types of tickets involved. There are children tickets and adult tickets.
- Create a table to organize the information.
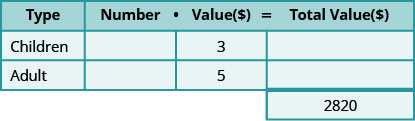
Step 2. Identify what we are looking for.
- We are looking for the number of children and adult tickets.
Step 3. Name. Represent the number of each type of ticket using variables.
- We know the total number of tickets sold was 810.
- This means the number of children’s tickets plus the number of adult tickets must add up to 810.
- Let \(c\) be the number of children tickets.
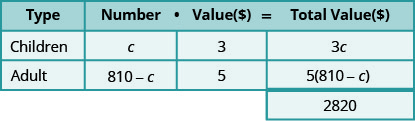
- Then \(810−c\) is the number of adult tickets.
- Multiply the number times the value to get the total value of each type of ticket.
Step 4. Translate.
Write the equation by adding the total values of each type of ticket.
Step 5. Solve the equation.
\[\begin{align*} 3 c+5(810-c) &=2,820 \\ 3 c+4,050-5 c &=2,820 \\-2 c &=-1,230 \\ c &=615 \text { children tickets } \end{align*}\]
How many adults?
\[\begin{array}{c}{810-c} \\ {810-615} \\ {195 \text { adult tickets }}\end{array} \nonumber\]
Step 6. Check the answer. There were 615 children’s tickets at $3 each and 195 adult tickets at $5 each. Is the total value $2,820?
\[\begin{array}{rrl}{615 \cdot 3} &{=} & {1845} \\ {195 \cdot 5} &{=} & {\underline{975}} \\ {} &{} &{2,820\checkmark} \end{array} \nonumber\]
Step 7. Answer the question. Galen sold 615 children’s tickets and 195 adult tickets.
Try It \(\PageIndex{9}\)
During her shift at the museum ticket booth, Leah sold 115 tickets for a total of $1,163. Adult tickets cost $12 and student tickets cost $5. How many adult tickets and how many student tickets did Leah sell?
- Answer
-
84 adult tickets, 31 student tickets
Try It \(\PageIndex{10}\)
A whale-watching ship had 40 paying passengers on board. The total collected from tickets was $1,196. Full-fare passengers paid $32 each and reduced-fare passengers paid $26 each. How many full-fare passengers and how many reduced-fare passengers were on the ship?
- Answer
-
26 full-fare, 14 reduced fare
Now, we’ll do one where we fill in the table all at once.
Example \(\PageIndex{6}\)
Monica paid $8.36 for stamps. The number of 41-cent stamps was four more than twice the number of two-cent stamps. How many 41-cent stamps and how many two-cent stamps did Monica buy?
Solution
The types of stamps are 41-cent stamps and two-cent stamps. Their names also give the value!
“The number of 41-cent stamps was four more than twice the number of two-cent stamps.”
\[\begin{array}{l}{\text { Let } x=\text { number of } 2 \text { -cent stamps. }} \\ {2 x+4=\text { number of } 41-\text { cent stamps }}\end{array} \nonumber\]
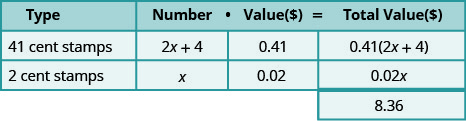
\[\begin{array}{lr} {\text{Write the equation from the total values.}} &{0.41(2x + 4) + 0.02x = 8.36} \\ {} &{0.82x + 1.64 + 0.02x = 8.36} \\ {} &{0.84x + 1.64 = 8.36} \\ {\text{Solve the equation.}} &{0.84x = 6.72} \\ {} &{x = 8} \\\\ {\text{Monica bought eight two-cent stamps.}} &{} \\{\text{Find the number of 41-cent stamps she bought}} &{2x + 4 \text{ for } x = 8} \\{\text{by evaluating}} &{2x + 4} \\{} &{2(8) + 4} \\ {} &{20} \end{array} \nonumber\]
Check.
\[\begin{array} {rll} {8(0.02) + 20(0.41)} &{\stackrel{?}{=}} &{8.36} \\ {0.16 + 8.20} &{\stackrel{?}{=}} &{8.36} \\{8.36} &{=} &{8.46\checkmark} \end{array}\]
\[\begin{array} {ll} \\ {} &{\text{Monica bought eight two-cent stamps and 20}} \\ {} &{\text{41-cent stamps}} \end{array} \nonumber\]
Try It \(\PageIndex{11}\)
Eric paid $13.36 for stamps. The number of 41-cent stamps was eight more than twice the number of two-cent stamps. How many 41-cent stamps and how many two-cent stamps did Eric buy?
- Answer
-
32 at $0.41, 12 at $0.02
Try It \(\PageIndex{12}\)
Kailee paid $12.66 for stamps. The number of 41-cent stamps was four less than three times the number of 20-cent stamps. How many 41-cent stamps and how many 20-cent stamps did Kailee buy?
- Answer
-
26 at $0.41, 10 at $0.20
Solve Mixture Word Problems
Now we’ll solve some more general applications of the mixture model. Grocers and bartenders use the mixture model to set a fair price for a product made from mixing two or more ingredients. Financial planners use the mixture model when they invest money in a variety of accounts and want to find the overall interest rate. Landscape designers use the mixture model when they have an assortment of plants and a fixed budget, and event coordinators do the same when choosing appetizers and entrees for a banquet.
Our first mixture word problem will be making trail mix from raisins and nuts.
Example \(\PageIndex{7}\)
Henning is mixing raisins and nuts to make 10 pounds of trail mix. Raisins cost $2 a pound and nuts cost $6 a pound. If Henning wants his cost for the trail mix to be $5.20 a pound, how many pounds of raisins and how many pounds of nuts should he use?
Solution
As before, we fill in a chart to organize our information.
The 10 pounds of trail mix will come from mixing raisins and nuts.
\[\begin{array}{l}{\text { Let } x=\text { number of pounds of raisins. }} \\ {10-x=\text { number of pounds of nuts }}\end{array} \nonumber\]
We enter the price per pound for each item.
We multiply the number times the value to get the total value.
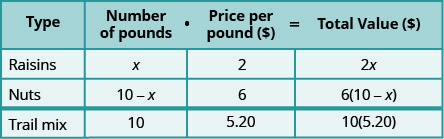
Notice that the last line in the table gives the information for the total amount of the mixture.
We know the value of the raisins plus the value of the nuts will be the value of the trail mix.
| Write the equation from the total values. | 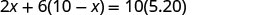 |
| Solve the equation. | 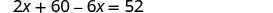 |
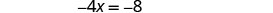 |
|
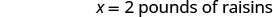 |
|
| Find the number of pounds of nuts. | 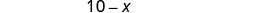 |
 |
|
| 8 pounds of nuts | |
| Check. \(\begin{array}{rll} {2($2) + 8($6)} &{\stackrel{?}{=} } &{10($5.20)} \\ {$4 + $48} &{\stackrel{?}{=} } &{$52} \\ {$52} &{=} &{$52\checkmark} \end{array}\) |
|
| Henning mixed two pounds of raisins with eight pounds of nuts. |
Try It \(\PageIndex{13}\)
Orlando is mixing nuts and cereal squares to make a party mix. Nuts sell for $7 a pound and cereal squares sell for $4 a pound. Orlando wants to make 30 pounds of party mix at a cost of $6.50 a pound, how many pounds of nuts and how many pounds of cereal squares should he use?
- Answer
-
5 pounds cereal squares, 25 pounds nuts
Try It \(\PageIndex{14}\)
Becca wants to mix fruit juice and soda to make a punch. She can buy fruit juice for $3 a gallon and soda for $4 a gallon. If she wants to make 28 gallons of punch at a cost of $3.25 a gallon, how many gallons of fruit juice and how many gallons of soda should she buy?
- Answer
-
21 gallons of fruit punch, 7 gallons of soda
We can also use the mixture model to solve investment problems using simple interest. We have used the simple interest formula, \(I=Prt\), where \(t\) represented the number of years. When we just need to find the interest for one year, \(t=1\), so then \(I=Pr\).
Example \(\PageIndex{8}\)
Stacey has $20,000 to invest in two different bank accounts. One account pays interest at 3% per year and the other account pays interest at 5% per year. How much should she invest in each account if she wants to earn 4.5% interest per year on the total amount?
Solution
We will fill in a chart to organize our information. We will use the simple interest formula to find the interest earned in the different accounts.
The interest on the mixed investment will come from adding the interest from the account earning 3% and the interest from the account earning 5% to get the total interest on the $20,000.
\[\begin{aligned} \text { Let } x &=\text { amount invested at } 3 \% \\ 20,000-x &=\text { amount invested at } 5 \% \end{aligned}\]
The amount invested is the principal for each account.
We enter the interest rate for each account.
We multiply the amount invested times the rate to get the interest.
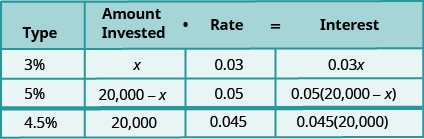
Notice that the total amount invested, 20,000, is the sum of the amount invested at 3% and the amount invested at 5%. And the total interest, \(0.045(20,000)\), is the sum of the interest earned in the 3% account and the interest earned in the 5% account.
As with the other mixture applications, the last column in the table gives us the equation to solve.
| Write the equation from the interest earned. Solve the equation. |
\(\begin{array}{rll}{0.03x + 0.05(20000-x)} &{=} &{0.045(20000)} \\\\ {0.03x + 1000 - 0.05x} &{=} &{900} \\ {-0.02x} &{=} &{-100} \\ {x} &{=} &{5000} \\ {\text{amount invested at 3%}} \end{array}\) |
| Find the amount invested at 5%. |    |
|
Check. |
|
| Stacey should invest $5,000 in the account that earns 3% and $15,000 in the account that earns 5%. |
Try It \(\PageIndex{15}\)
Remy has $14,000 to invest in two mutual funds. One fund pays interest at 4% per year and the other fund pays interest at 7% per year. How much should she invest in each fund if she wants to earn 6.1% interest on the total amount?
- Answer
-
$4,200 at 4%, $9,800 at 7%
Try It \(\PageIndex{16}\)
Marco has $8,000 to save for his daughter’s college education. He wants to divide it between one account that pays 3.2% interest per year and another account that pays 8% interest per year. How much should he invest in each account if he wants the interest on the total investment to be 6.5%?
- Answer
-
$2,500 at 3.2%, $5,500 at 8%
Key Concepts
- Total Value of Coins For the same type of coin, the total value of a number of coins is found by using the model.
number·value=total value where number is the number of coins and value is the value of each coin; total value is the total value of all the coins - Problem-Solving Strategy—Coin Word Problems
- Read the problem. Make all the words and ideas are understood. Determine the types of coins involved.
- Create a table to organize the information.
- Label the columns type, number, value, total value.
- List the types of coins.
- Write in the value of each type of coin.
- Write in the total value of all the coins.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
Use variable expressions to represent the number of each type of coin and write them in the table.
Multiply the number times the value to get the total value of each type of coin. - Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the sentence into an equation.
Write the equation by adding the total values of all the types of coins. - Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- Read the problem. Make all the words and ideas are understood. Determine the types of coins involved.
Glossary
- mixture problems
- Mixture problems combine two or more items with different values together.


