2.3e: Exercises - Transformations
( \newcommand{\kernel}{\mathrm{null}\,}\)
A: Concepts
Exercise 2.3e.A
1) When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal shift from a vertical shift?
2) When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal stretch from a vertical stretch?
3) When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal compression from a vertical compression?
4) When examining the formula of a function that is the result of multiple transformations, how can you tell a reflection with respect to the x-axis from a reflection with respect to the y-axis?
5) How can you determine whether a function is odd or even from the formula of the function?
- Answers to Odd Exercises:
-
1. A horizontal shift results when a constant is added to or subtracted from the input. A vertical shifts results when a constant is added to or subtracted from the output.
3. A horizontal compression results when a constant greater than 1 is multiplied by the input. A vertical compression results when a constant between 0 and 1 is multiplied by the output.
5. For a function f, substitute (−x) for (x) in f(x). Simplify. If the resulting function is the same as the original function, f(−x)=f(x), then the function is even. If the resulting function is the opposite of the original function, f(−x)=−f(x), then the original function is odd. If the function is not the same or the opposite, then the function is neither odd nor even.
B: Describe transformations of a function written in function notation
Exercise 2.3e.B
★ Describe how the graph of the function is a transformation of the graph of the original function f.
|
6) y=f(x−49) 7) y=f(x+43) 8) y=f(x+3) 9) y=f(x−4) |
10) y=f(x)+5 11) y=f(x)+8 12) y=f(x)−2 13) y=f(x)−7 |
14) y=f(x−2)+3 15) y=f(x+4)−1 16) g(x)=f(−x) 17) g(x)=−f(x) |
18) g(x)=6f(x) 19) g(x)=4f(x) 20) g(x)=f(2x) 21) g(x)=f(5x) |
22) g(x)=f(15x) 23) g(x)=f(13x) 24) g(x)=−f(3x) 25) g(x)=3f(−x) |
- Answers to Odd Exercises:
-
7. The graph of f(x+43) is a horizontal shift to the left 43 units of the graph of f.
9. The graph of f(x−4) is a horizontal shift to the right 4 units of the graph of f.
11. The graph of f(x)+8 is a vertical shift up 8 units of the graph of f.
13. The graph of f(x)−7 is a vertical shift down 7 units of the graph of f.
15. The graph of f(x+4)−1 is a horizontal shift left 4 units and vertical shift down 1 unit of the graph of f.
17. The graph of g is a vertical reflection (across the x-axis) of the graph of f.
19. The graph of g is a vertical stretch by a factor of 4 of the graph of f.
21. The graph of g is a horizontal compression by a factor of 15 of the graph of f.
23. The graph of g is a horizontal stretch by a factor of 3 of the graph of f.
25. The graph of g is a horizontal reflection across the y-axis and a vertical stretch by a factor of 3 of the graph of f.
C: Graph transformations of a basic function
Exercise 2.3e.C
★ Begin by graphing the basic quadratic function f(x)=x2. State the transformations needed to apply to f to graph the function below. Then use transformations to graph the function.
|
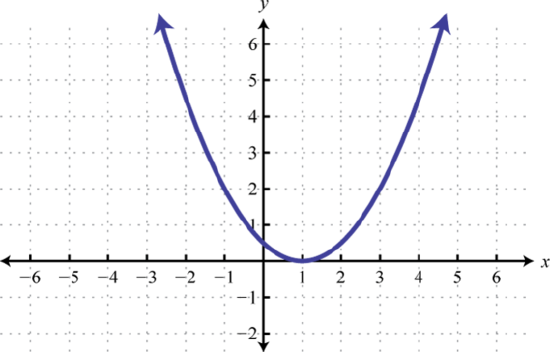
27. g(x)=x2+1 28. g(x)=x2−4 29. g(x)=(x−5)2 30. g(x)=(x+1)2 |
31. g(x)=(x−5)2+2 32. g(x)=(x+2)2−5 33. f(t)=(t+1)2−3 34. f(x)=−(x+2)2 |
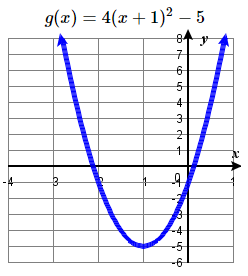
35. f(x)=−x2+6 36. g(x)=−2x2 37. g(x)=4(x+1)2−5 38. g(x)=5(x+3)2−2 |
39. h(x)=12(x−1)2 40. h(x)=13(x+2)2 41. f(x)=(−12x−3)2+1 42. g(x)=(−2x+3)2−4 |
★ Begin by graphing the square root function f(x)=√x. State the transformations needed to apply to f to graph the function below. Then use transformations to graph the function.
|
43. g(x)=√x−5 44. g(x)=√x−5 45. g(x)=√x−2+1 46. g(x)=√x+2+3 |
47. a(x)=√−x+4 48. m(t)=3−√t+2 49. h(x)=√−x+2 50. g(x)=−√x+2 |
51. g(x)=−12√x−3 52. h(x)=−√x−2+1 53. f(x)=4√x−1+2 54. f(x)=−5√x+2 |
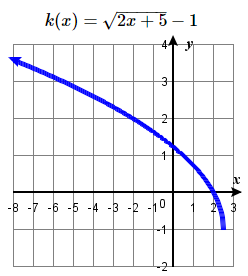
55. k(x)=√2x+5−1 56.1 a(x)=√13x−4 56.2 b(x)=√3−x+2 |
★ Begin by graphing the absolute value function f(x)=|x|. State the transformations needed to apply to f to graph the function below. Then use transformations to graph the function.
|
57. h(x)=|x+4| 58. h(x)=|x−4| 59. h(x)=|x−1|−3 60. h(x)=|x+2|−5 |
61. g(x)=−|x−1| 62. h(x)=|x−1|+4 63. f(x)=−3|x| 64. f(x)=−|x|−3 |
65. h(x)=−2|x−4|+3 66. n(x)=13|x−2| |
67. h(x)=|−3x+4|−2 68. g(x)=|13x−2|+1 |
★ Begin by graphing the standard cubic function f(x)=x3. State the transformations needed to apply to f to graph the function below. Then use transformations to graph the function.
|
69. h(x)=(x−2)3 70. h(x)=x3+4 71. h(x)=(x−1)3−4 |
72. h(x)=(x+1)3+3 73. g(x)=−(x+2)3 74. k(x)=(x−2)3−1 |
75. g(x)=−x3+4 76. m(x)=12x3 77. g(x)=−14(x+3)3−1 |
78. q(x)=(14x)3+1 79. p(x)=(13x)3−3 |
★ Begin by graphing the appropriate parent function : the basic cube root function f(x)=3√x, constant function f(x)=0, or linear function f(x)=x. Then use transformations of this graph to graph the given function.
|
81. g(x)=3√x−1 82. g(x)=3√x−1 |
83. g(x)=3√x−2+6 84. g(x)=3√x+8−4 84.1 g(x)=3√−x+3−2 |
84.1 g(x)=−3√x−1+2 85. g(x)=−23√x+3+4 86. g(x)=3√−2x−5−1 |
87. f(x)=x+3 88. h(x)=−2x+1 89. g(x)=−4 |
★ Begin by graphing the basic reciprocal function f(x)=1x. State the transformations needed to apply to f to graph the function below. Then use transformations to graph the function.
|
91. f(x)=1x−2 92. f(x)=1x+3 93. f(x)=1x+5 |
94. f(x)=1x−3 95. f(x)=1x+1−2 96. f(x)=1x−3+3 |
97. f(x)=−1x+2 98. f(x)=−1x 99.p(x)=−1x+1+2 |
100.1 a(x)=2x−3−5 100.2 b(x)=12x+6+4 |
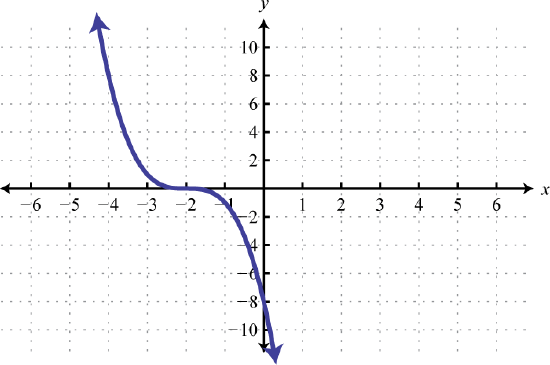
- Answers to Odd Numbered Exercises for the Squaring Function:
- Squaring Function
27. y=x2; Shift up 1 unit; domain: ℝ; range: [1,∞)
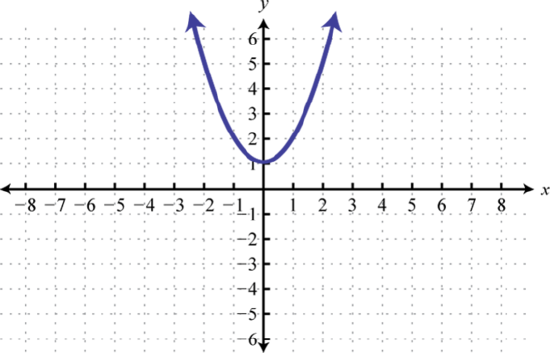
g(x)=x2+1 29. y=x2; Shift right 5 units; domain: ℝ; range: [0,∞)
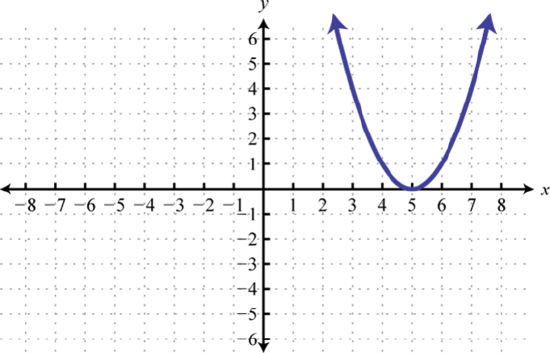
g(x)=(x−5)2 31. y=x2; Shift right 5 units and up 2 units; domain: ℝ; range: [2,∞)
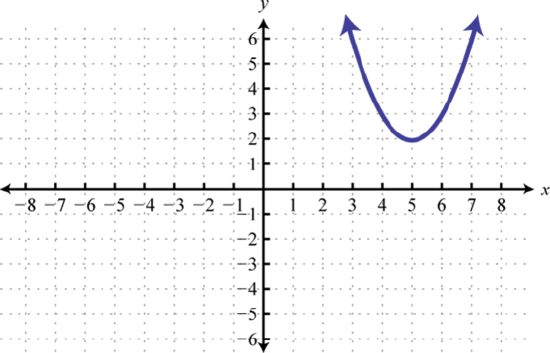
g(x)=(x−5)2+2 33. Shift left 1 unit and down 3 units;
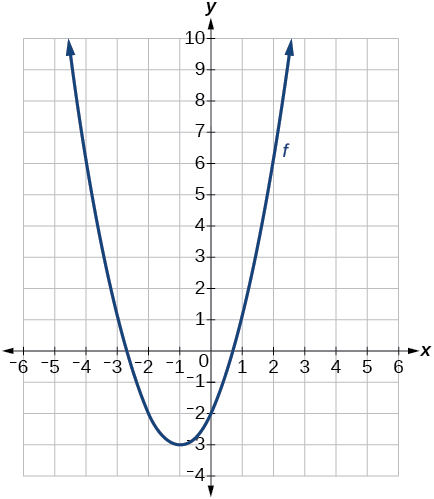
f(t)=(t+1)2−3#35 Reflect over x-axis, up 6 units.
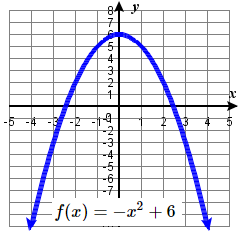
37 f(x)=x2 is shifted to the left 1 unit, stretched vertically by a factor of 4, and shifted down 5 units.
39. Shift right 1 unit, and vertically shrink by a factor of 12
h(x)=12(x−1)2 #41 Shift right 3, reflect over y-axis, horizontally stretch by a factor of 2, up 1 units.
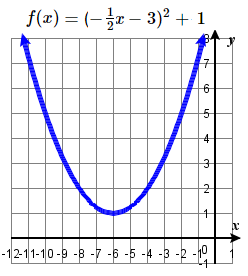
for # 41, if f(x)=(−12x−3)2+1 is rewritten as
f(x)=(−12(x+6))2+1 ,
then the transformations would be
horizontal stretch by a factor of 2, reflect in y-axis (no change), left 6, up 1.
- Answers to Odd Numbered Exercises for the Square Root Function
-
Square Root Function
43. y=√x; Shift down 5 units; domain: [0,∞); range: [−5,∞)
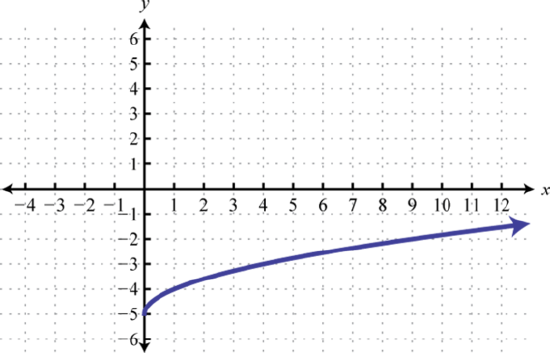
g(x)=√x−5 45. y=√x; Shift right 2 units and up 1 unit; domain: [2,∞); range: [1,∞)
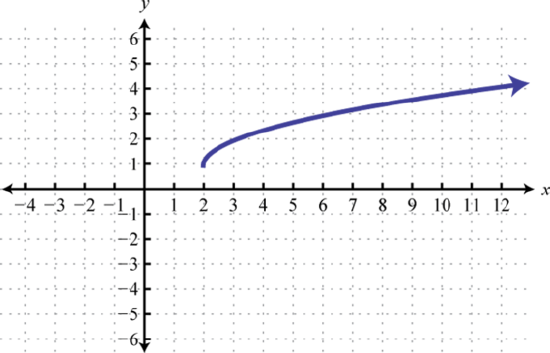
g(x)=√x−2+1 47 The graph of f(x)=√x is shifted left 4 units and then reflected across the y-axis.
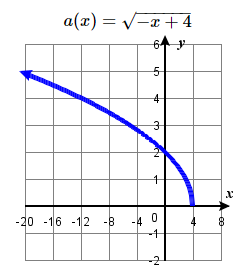
49. Reflect over y-axis, up 2
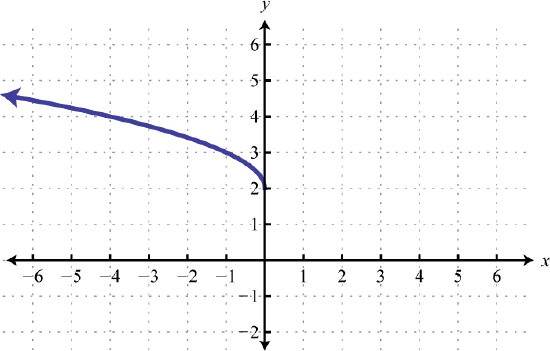
h(x)=√−x+2 51. Right 3, Reflect over x axis, Vertically compressed by a factor of 1/2.
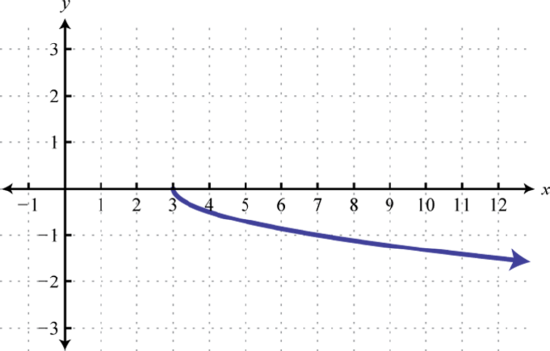 g(x)=−12√x−3
g(x)=−12√x−353. Right 1, Vertically stretched by a factor of 4, up 2
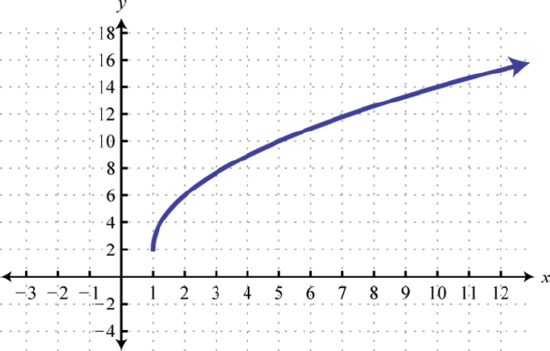
f(x)=4√x−1+2 #55 Horizontal compression by 1/2, shift left 2.5, down 1 unit.
- Answers to Odd Numbered Exercises for the Absolute Value Function:
-
Absolute Value Function
57. y=|x|; Shift left 4 units; domain: ℝ; range: [0,∞)
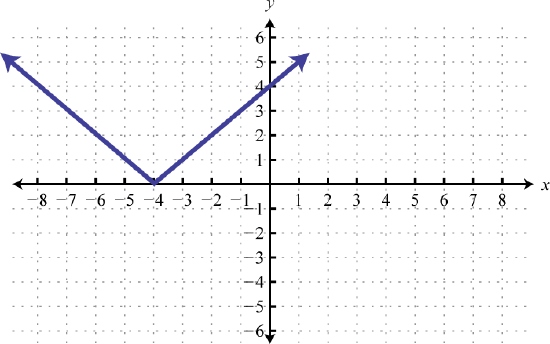
h(x)=|x+4| .
59. y=|x|; Shift right 1 unit and down 3 units; domain: ℝ; range: [−3,∞)

h(x)=|x−1|−3 .
61. Right 1, Reflect over x-axis
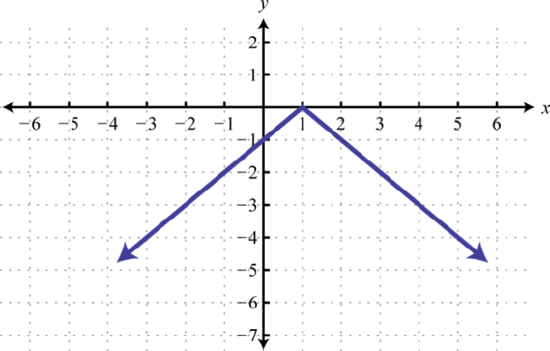
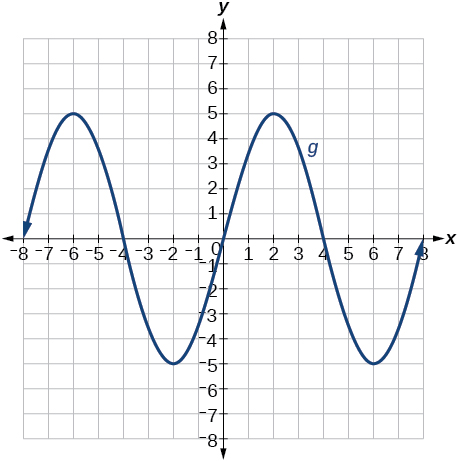
g(x)=−|x−1| .
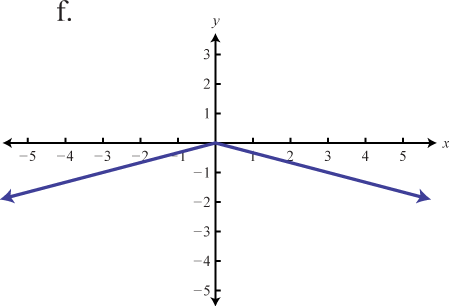
63. Reflect over x-axis, vertically stretch by a factor of 3
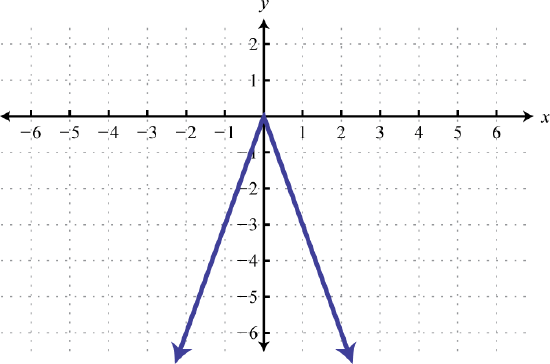
f(x)=−3|x| 65 The graph of f(x)=|x| is shifted horizontally 4 units to the right, stretched vertically by a factor of 2, reflected across the horizontal axis, then shifted up 3 units.
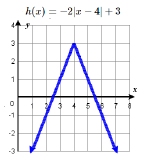
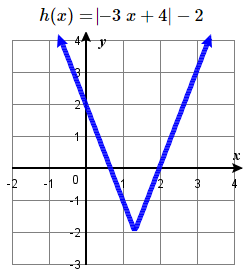
67. h(x)=|−3(x−43)|−2 ⟶ Horizontally compress by a factor of 13, right 43, down 2
- Answers to Odd Numbered Exercises for the Cubing Function
-
Cubing Function
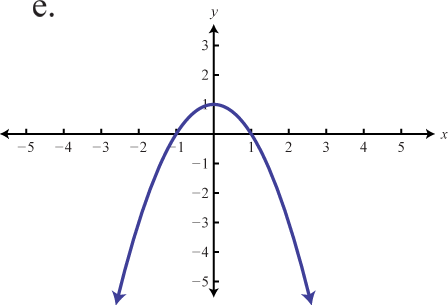
69. y=x3 ; Shift right 2 units; domain: ℝ; range: ℝ
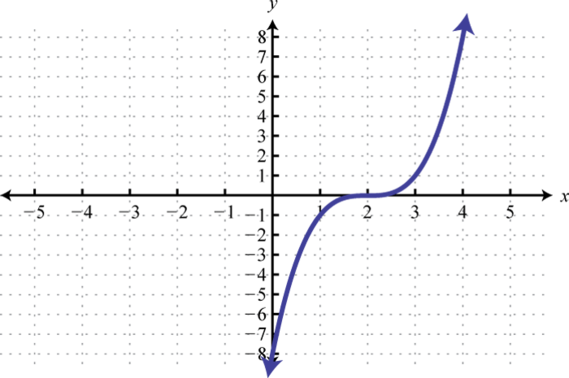
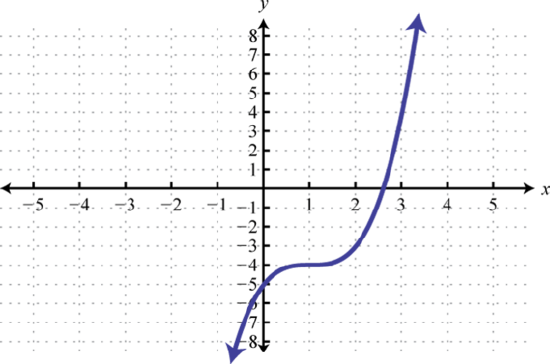
h(x)=(x−2)3 71. y=x3; Shift right 1 unit and down 4 units; domain: ℝ; range: ℝ
h(x)=(x−1)3−4 73. Left 2 units, reflect over x-axis
g(x)=−(x+2)3 75. Reflect over x-axis, up 4 units
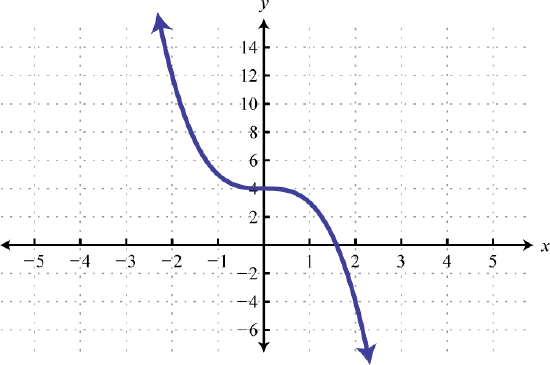
g(x)=−x3+4 77. Left 3 units, reflect over x-axis, vertically shrink by a factor of 14, down 1 unit
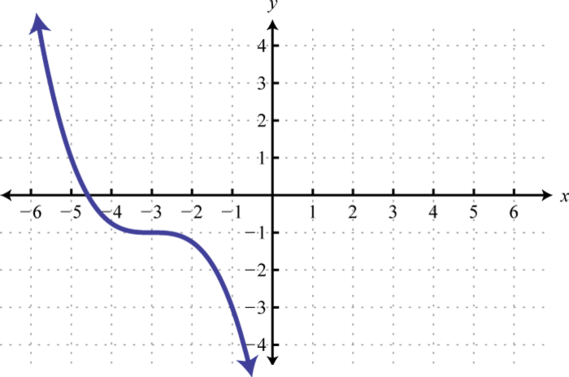
g(x)=−14(x+3)3−1 79. Stretch horizontally by a factor of 3 and shift vertically downward by 3 units.
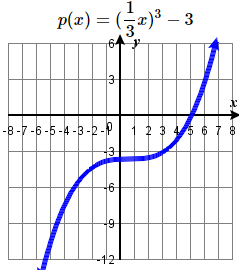
- Answers to Odd Numbered Exercises for the Cube Root, Linear and Constant Functions
-
Cube Root, Linear, Constant Functions
81. y=3√x; Shift down 1
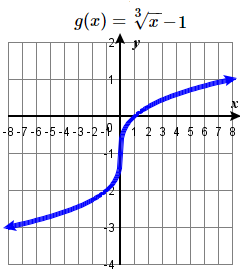
83. y=3√x; Shift up 6 units and right 2 units; domain: ℝ; range: ℝ
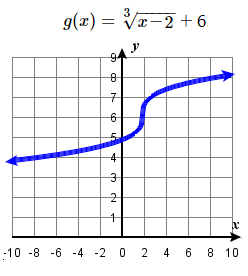
85. y=3√x; Left 3, reflect over x-axis, vertically stretch by a factor of 2, up 4.
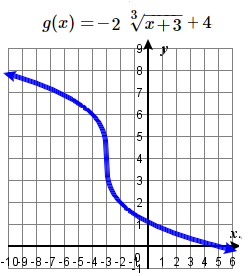
87. y=x; Shift up 3 units; domain: R; range: R
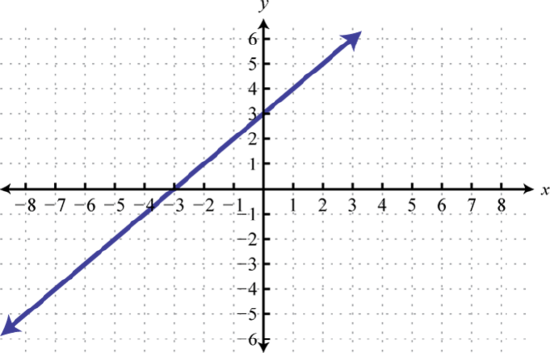
f(x)=x+3 89. Basic graph y=−4; domain: ℝ; range: {−4}

g(x)=−4
- Answers to Odd Numbered Exercises for the Reciprocal Function:
-
Reciprocal Function
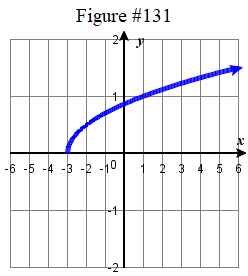
91. y=1x; Shift right 2 units; domain: (−∞,2)∪(2,∞); range: (−∞,0)∪(0,∞)
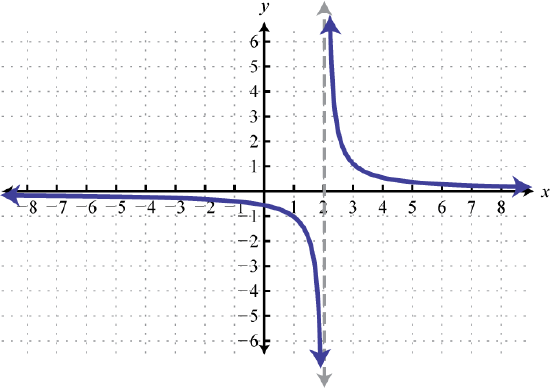
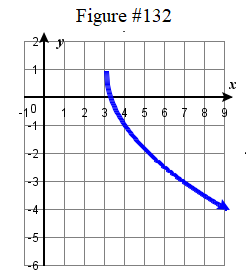
f(x)=1x−2 93. y=1x; Shift up 5 units;
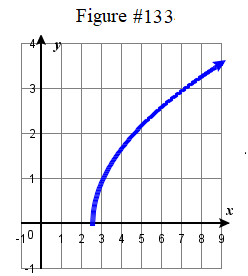
domain: (−∞,0)∪(0,∞);
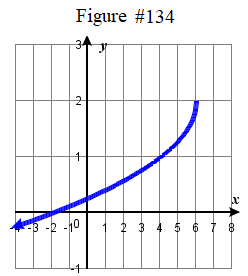
range: (−∞,1)∪(1,∞)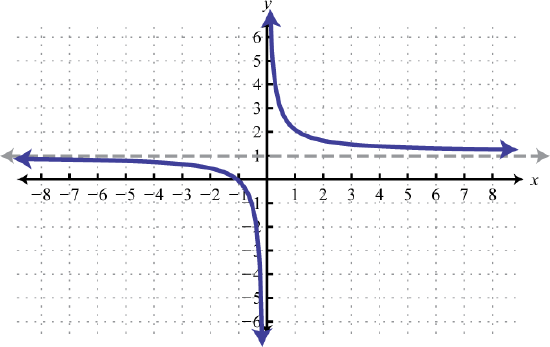
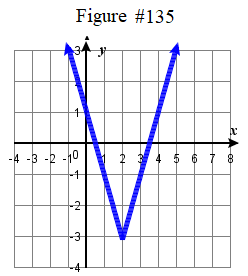
f(x)=1x+5 ⋆
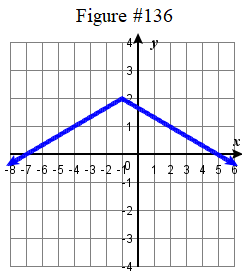
95. y=1x; Shift left 1 unit and down 2 units; domain: (−∞,−1)∪(−1,∞); range: (−∞,−2)∪(−2,∞)
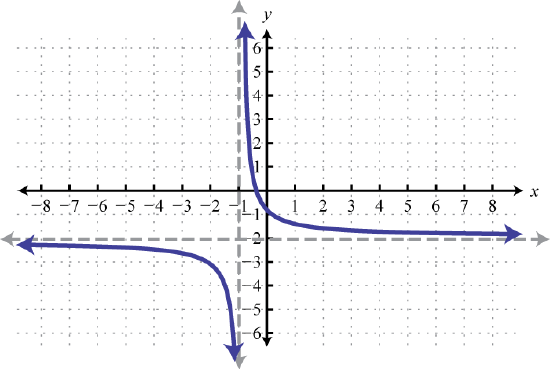
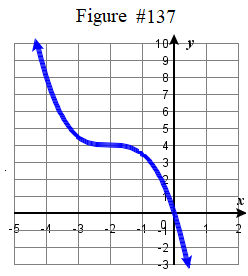
f(x)=1x+1−2 97
97. Left 2 units, reflect over x-axis
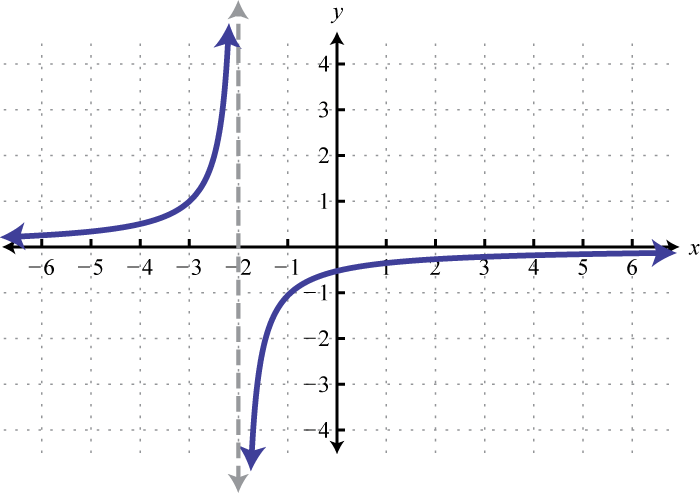
f(x)=−1x+2
#99 Left 1 unit, reflect over x-axis, up 2 units.
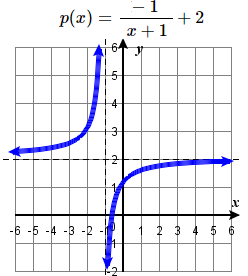
D: Graph Transformations of a Graph
Exercise 2.3e.D
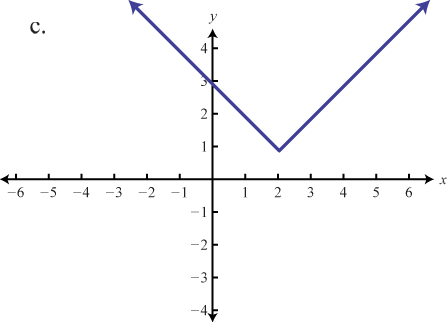
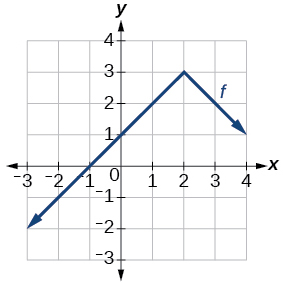
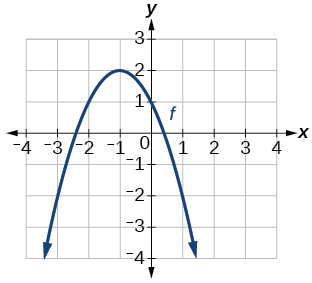
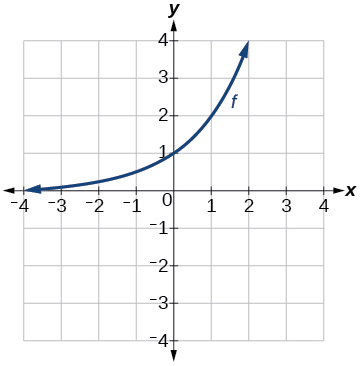
★ Use the graph of f(x) shown in the Figure below to sketch a graph of each transformation of f(x).
|
101. h(x)=2x−3 102. a) g(x)=2x+1 b) w(x)=2x−1 |
103. a) g(x)=−f(x) b) g(x)=f(x−2) 104. a) g(x)=f(x)−2 b) g(x)=f(x+1) |
106. Given the graph of f(x) below, sketch the graph for the following transformations of f
|
|
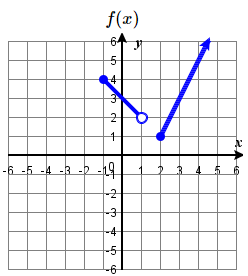 |
- Answers to Odd Exercises:
-
101
103. a
103. b
E: Match transformations of functions with graphs
Exercise 2.3e.E
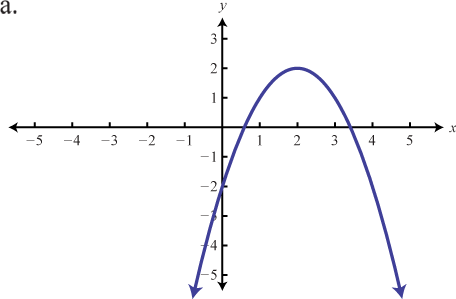
★ Match the graph to the function definition.
|
107. f(x)=√x+4 108. f(x)=|x−2|−2 |
109. f(x)=√x+1−1 110. f(x)=|x−2|+1 |
111. f(x)=√x+4+1 112. f(x)=|x+2|−2 |
|
|
|
|
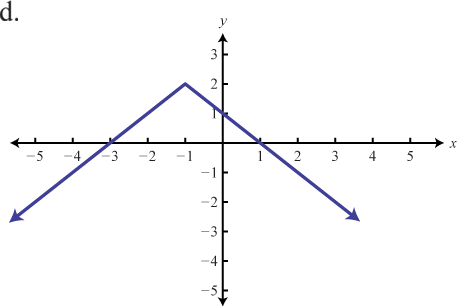
Match the graph to the given function definition.
|
113. f(x)=−3|x| 114. f(x)=−(x+3)2−1 |
115. f(x)=−|x+1|+2 116. f(x)=−x2+1 |
117. f(x)=−13|x| 118. f(x)=−(x−2)2+2 |

⋆ |
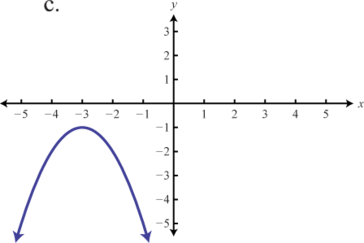
⋆ |
⋆ |
- Answers to Odd Exercises:
-
part 1 answers 107e, 109d, 111f, part 2 Answers: 113.b, 115.d, 117.f
F: Construct equations from graphs of transformed basic functions
Exercise 2.3e.F
★ Write an equation for each graphed function by using transformations of the graphs of one of the toolkit functions.
119. |
120. |
121.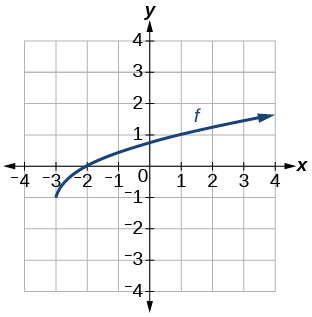 |
122.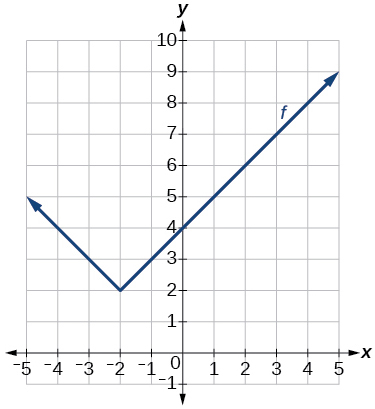 |
123.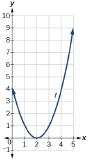 |
124.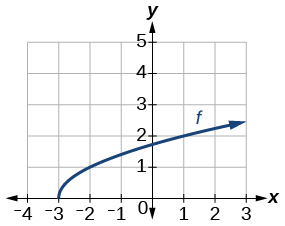 |
125.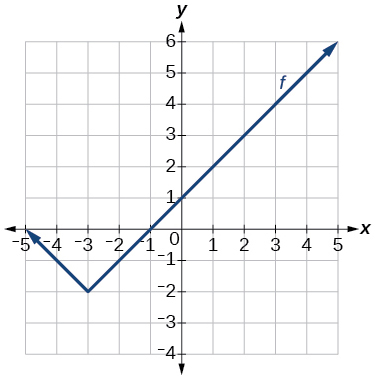 |
126.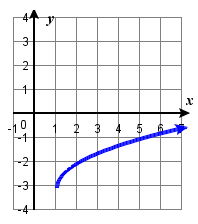 |
127.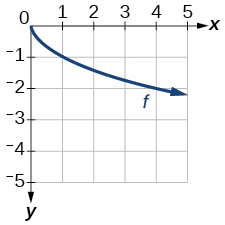 |
128.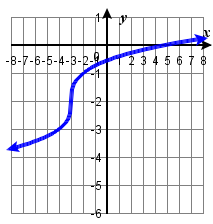 |
129. |
|
|
130. (a) |
130. (b) |
130. (c)
|
|
- Answers to Odd Exercises:
-
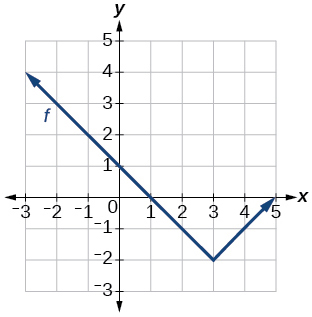
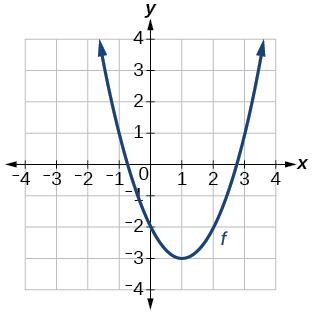
119. f(x)=|x−3|−2
121. f(x)=√x+3−1123. f(x)=(x−2)2
125. f(x)=|x+3|−2127. f(x)=−√x
129. f(x)=−(x+1)2+2
★ Write an equation that represents the function whose graph is given.
|
131.
|
132.
|
133.
|
|
134.
|
135.
|
136.
|
|
137.
|
138.
|
139.
|
- Answers to Odd Exercises:
-
131. f(x)=12√x+3 133. f(x)=√(2x−5)
135. f(x)=2|x−2|−3137. f(x)=−12(x+2)3+4 139. f(x)=1x+6+4
G: Construct a formula from a description
Exercise 2.3e.G
★ Write a formula for the function with the following transformations
141. Write a formula for the function obtained when the graph of f(x)=|x| is shifted down 3 units and right 1 unit.
142. Write a formula for the function obtained when the graph of f(x)=1x is shifted down 4 units and right 3 units.
143. Write a formula for the function obtained when the graph of f(x)=1x2 is shifted up 2 units and left 4 units.
144. Write a formula for the function obtained when the graph of f(x)=√x is shifted up 1 unit and left 2 units.
145. The graph of f(x)=|x| is reflected over the y-axis and horizontally compressed by a factor of 14.
146. The graph of f(x)=√x is reflected over the x-axis and horizontally stretched by a factor of 2.
147. The graph of f(x)=1x2 is vertically compressed by a factor of 13, then shifted left 2 units and down 3 units.
148. The graph of f(x)=1x is vertically stretched by a factor of 8, then shifted to the right 4 units and up 2 units.
149. The graph of f(x)=x2 is vertically compressed by a factor of 12, then shifted to the right 5 units and up 1 unit.
150. The graph of f(x)=x2 is horizontally stretched by a factor of 3, then shifted left 4 units and down 3 units.
- Answers to Odd Exercises:
-
141. g(x)=|x−1|−3
143. g(x)=1(x+4)2+2
145. g(x)=|−4x|
147. g(x)=13(x+2)2−3
149. g(x)=12(x−5)2+1
H: Construct equations from transformations of tabular values
Exercise 2.3e.H
★ Given tabular representations for the functions f, g, and h, write g(x) and h(x) as transformations of f(x).
155. Tabular representations for the functions f, g, and h are given below. Write g(x) and h(x) as transformations of f(x).
|
|
|
156. Tabular representations for the functions f, g, and h are given below. Write g(x) and h(x) as transformations of f(x).
|
|
|
- Answers to Odd Exercises:
-
155. g(x)=f(x−1), h(x)=f(x)+1.
I: Identify Increasing/decreasing Intervals
Exercise 2.3e.I
★ Use transformations to determine the interval(s) on which the function is increasing and decreasing.
| 151. g(x)=5(x+3)2−2 | 152. f(x)=4(x+1)2−5 | 153. k(x)=−3√x−1 | 154. a(x)=√−x+4 |
- Answers to Odd Exercises:
-
151. decreasing on (−∞,−3) and increasing on (−3,∞) 153. decreasing on (0,∞)
⋆


 Given the graph of
Given the graph of 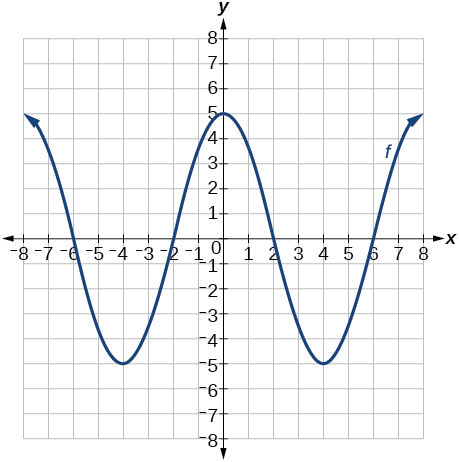 Given the graph of
Given the graph of