2.4: Function Compilations - Piecewise, Combinations, and Composition
- Page ID
- 34873
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Piecewise-Defined Functions
A piecewise function is a function whose definition changes depending on the value of its argument. The function is defined by different formulas for different parts of its domain.
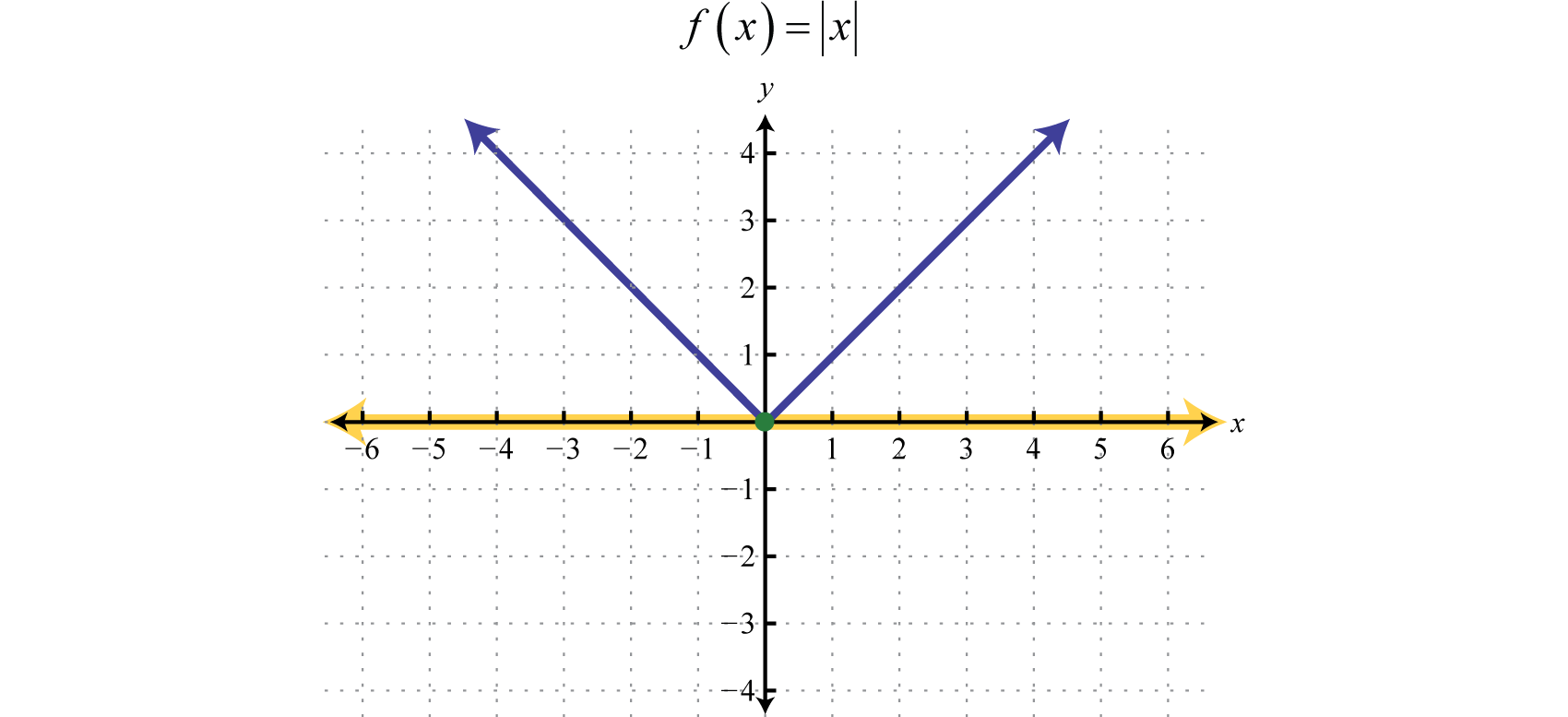
For example, we can write the absolute value function \(f(x) = |x|\) as a piecewise function:
\(f ( x ) = | x | = \left\{ \begin{array} { c l } { x } & { \text { if } x \geq 0 } \\ { - x } & { \text { if } x < 0 } \end{array} \right.\)
In this case, the definition used depends on the sign of the \(x\)-value. If the \(x\)-value is positive, \(x ≥ 0\), then the function is defined by \(f(x) = x\). And if the \(x\)-value is negative, \(x < 0\), then the function is defined by \(f(x) = −x\). The graphs of these two pieces are shown below.

The graph of the absolute function itself is the combination of these two pieces on the same rectangular coordinate plane. The resulting graph is illustrated below.
![]() How to: Given a piecewise function sketch a graph .
How to: Given a piecewise function sketch a graph .
- Indicate on the \(x\)-axis the boundaries defined by the intervals on each piece of the domain. Each equation defines a graph for a column of the Cartesian coordinate plane.
- For each piece of the domain, graph on that interval using the corresponding equation pertaining to that piece. Do not graph two functions in the same interval because the graph would no longer be a graph of a function because it would fail the Vertical Line Test.
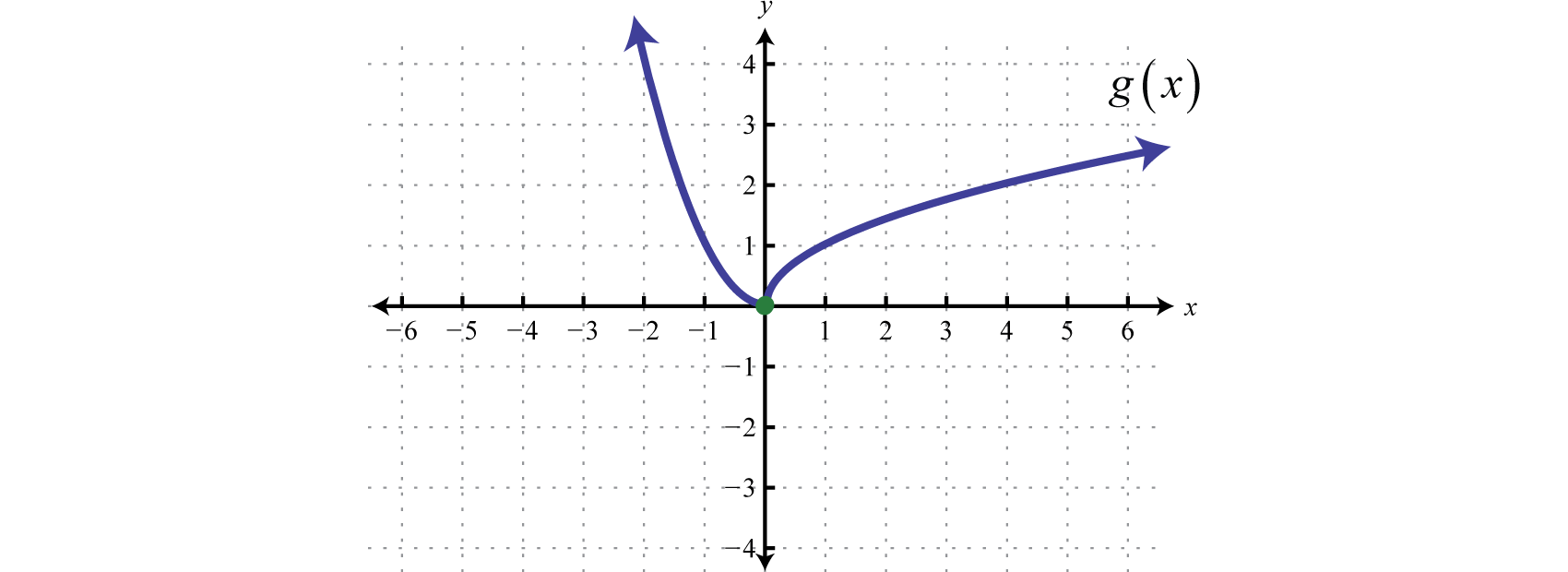
Example \(\PageIndex{1}\): Graph a 2-piece function
Graph: \(g ( x ) = \left\{ \begin{array} { c c c } { x ^ { 2 } } & { \text { if } } & { x < 0 } \\ { \sqrt { x } } & { \text { if } } & { x \geq 0 } \end{array} \right.\).
Solution
In this case, we graph the squaring function over negative \(x\)-values and the square root function over positive \(x\)-values.

Notice the open dot used at the origin for the squaring function and the closed dot used for the square root function. This was determined by the inequality that defines the domain of each piece of the function. The entire function consists of each piece graphed on the same coordinate plane.
Answer:
Example \(\PageIndex{2}\)
Sketch a graph of the following piecewise-defined function:
\[f(x)=\begin{cases}x+3, &x<1\\(x−2)^2, &x≥1\end{cases} \nonumber\]
Solution
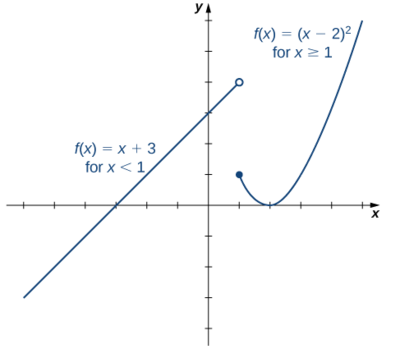 Graph the linear function \(y=x+3\) on the interval \((−∞,1)\) and graph the quadratic function \(y=(x−2)^2\) on the interval \([1,∞)\). Since the value of the function at \(x=1\) is given by the formula \(f(x)=(x−2)^2\), we see that \(f(1)=1\). To indicate this on the graph, we draw a closed circle at the point \((1,1)\). The value of the function is given by \(f(x)=x+2\) for all \(x<1\), but not at \(x=1\). To indicate this on the graph, we draw an open circle at \((1,4)\).
Graph the linear function \(y=x+3\) on the interval \((−∞,1)\) and graph the quadratic function \(y=(x−2)^2\) on the interval \([1,∞)\). Since the value of the function at \(x=1\) is given by the formula \(f(x)=(x−2)^2\), we see that \(f(1)=1\). To indicate this on the graph, we draw a closed circle at the point \((1,1)\). The value of the function is given by \(f(x)=x+2\) for all \(x<1\), but not at \(x=1\). To indicate this on the graph, we draw an open circle at \((1,4)\).
The figure at the right illustrates this piecewise-defined function that is linear for \(x<1\) and quadratic for \(x≥1.\)
![]() Try It \(\PageIndex{3}\)
Try It \(\PageIndex{3}\)
Graph the following piecewise functions.
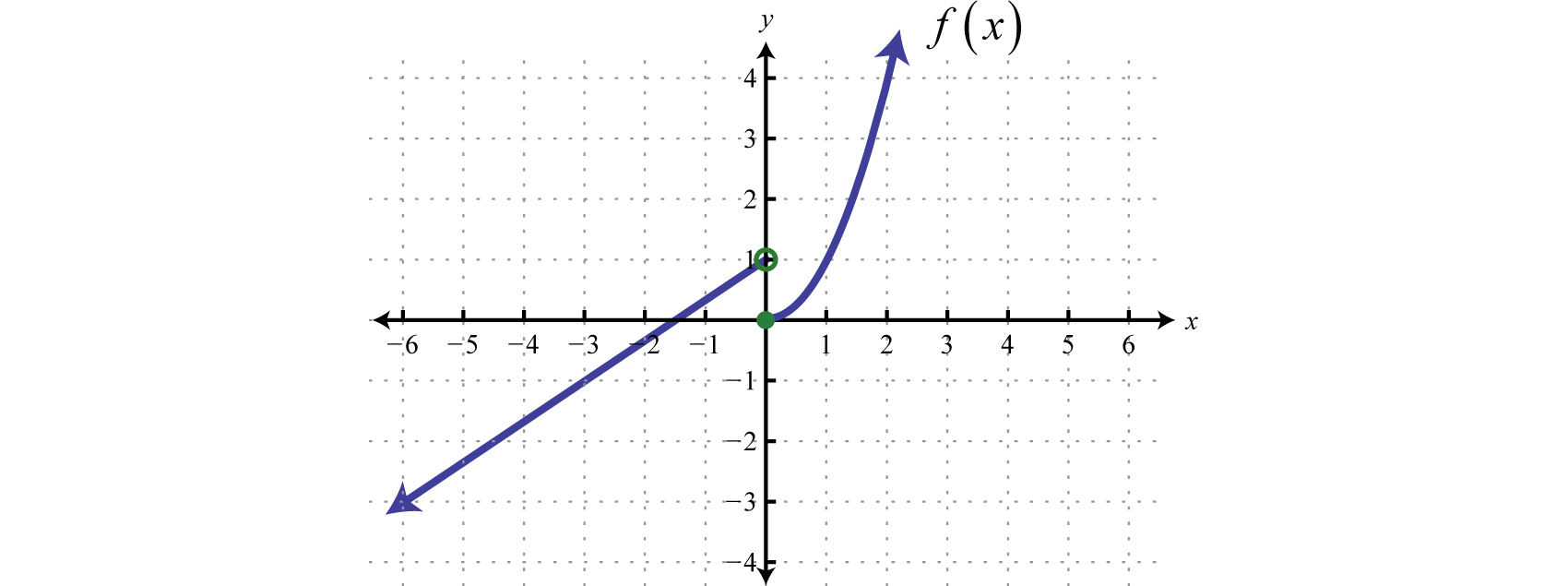
| a. \(f(x)=\begin{cases}2−x, x≤2\\x+2, x>2\end{cases}.\) | b. \(f ( x ) = \left\{ \begin{array} { l l } { \frac { 2 } { 3 } x + 1 } & { \text { if } x < 0 } \\ { x ^ { 2 } } & { \text { if } x \geq 0 } \end{array} \right.\). |
- Answer
-
a.
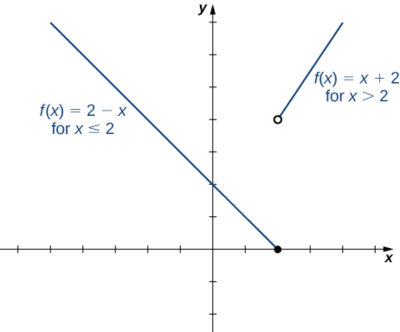
b.
Example \(\PageIndex{4}\): Graph a 3-piece function
Sketch a graph of the function.
\[f(x)= \begin{cases} x^2 & \text{if $x \leq 1$} \\ 3 &\text{if $1<x\leq2$} \\ x &\text{if $x>2$} \end{cases} \nonumber \]
Solution
Each of the component functions is from our library of toolkit functions, so we know their shapes. We can imagine graphing each function and then limiting the graph to the indicated domain. At the endpoints of the domain, we draw open circles to indicate where the endpoint is not included because of a less-than or greater-than inequality; we draw a closed circle where the endpoint is included because of a less-than-or-equal-to or greater-than-or-equal-to inequality.
Figure \(\PageIndex{4}\) shows the three components of the piecewise function graphed on separate coordinate systems.
![[Graph of each part of the piece-wise function f(x)]](https://math.libretexts.org/@api/deki/files/896/CNX_Precalc_Figure_01_02_023abc.jpg?revision=1&size=bestfit&width=692&height=232)
Figure \(\PageIndex{4}\): Graph of each part of the piece-wise function f(x)
(a)\( f(x)=x^2\) if \(x≤1\); (b) \(f(x)=3\) if \(1< x≤2\); (c) \(f(x)=x\) if \(x>2\)
|
Now that we have sketched each piece individually, we combine them in the same coordinate plane. See Figure \(\PageIndex{4s}\). Analysis Note that the graph does pass the vertical line test even at \(x=1\) and \(x=2\) because the points \((1,3)\) and \((2,2)\) are not part of the graph of the function, though \((1,1)\) and \((2, 3)\) are. |
![[Graph of the entire function.]](https://math.libretexts.org/@api/deki/files/897/CNX_Precalc_Figure_01_02_026.jpg?revision=1&size=bestfit&width=293&height=200)
|
Example \(\PageIndex{5}\):
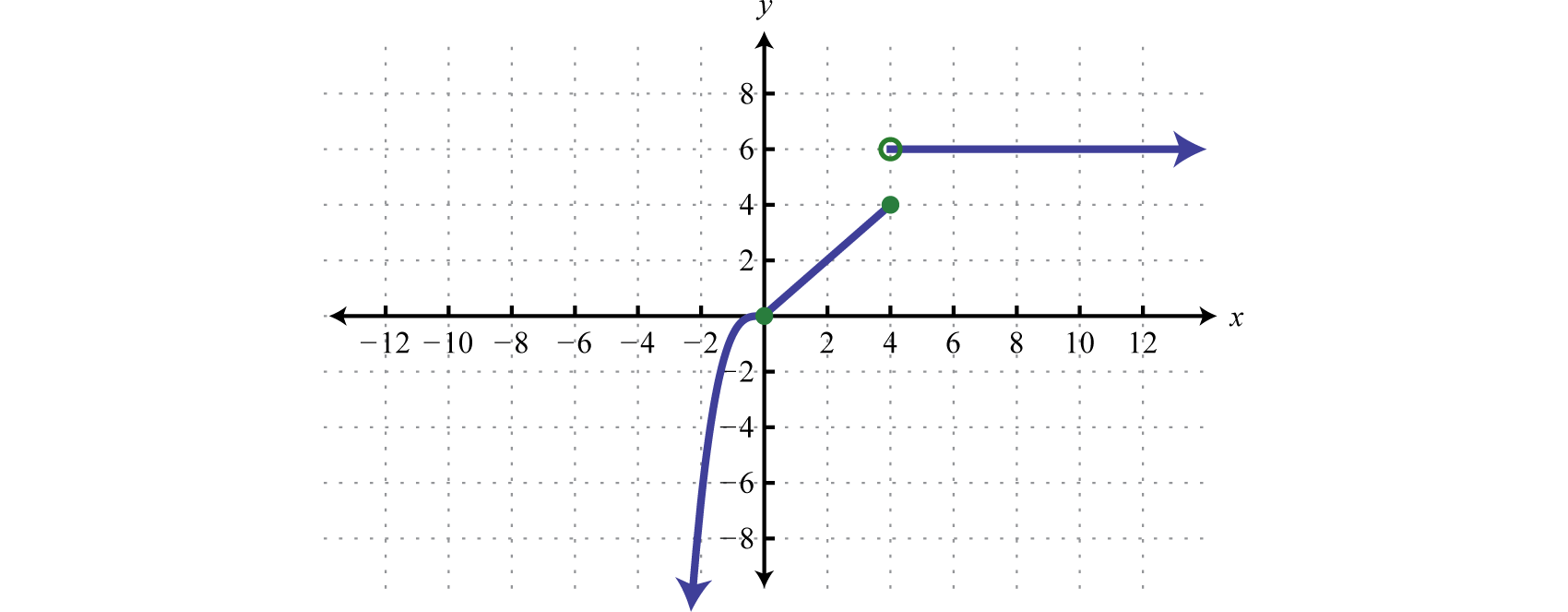
Graph: \(f ( x ) = \left\{ \begin{array} { l l } { x ^ { 3 } } & { \text { if } x < 0 } \\ { x } & { \text { if } 0 \leq x \leq 4 } \\ { 6 } & { \text { if } x > 4 } \end{array} \right.\).
Solution
In this case, graph the cubing function over the interval \((−∞,0)\). Graph the identity function over the interval \([0,4]\). Finally, graph the constant function \(f(x)=6\) over the interval \((4,∞)\). And because \(f(x)=6\) where \(x>4\), we use an open dot at the point \((4,6)\). Where \(x=4\), we use \(f(x)=x\) and thus \((4,4)\) is a point on the graph as indicated by a closed dot.
Answer:
![]() Try It \(\PageIndex{6}\)
Try It \(\PageIndex{6}\)
Graph the following piecewise function.
\[f(x)= \begin{cases} x^3 & \text{if $x < -1$} \\ -2 &\text{if $-1<x<4$} \\ \sqrt{x} &\text{if $x>4$} \end{cases} \nonumber \]
- Answer
-
![[Graph of f(x).]](https://math.libretexts.org/@api/deki/files/898/CNX_Precalc_Figure_01_02_027.jpg?revision=1&size=bestfit&width=347&height=291)
Figure \(\PageIndex{6s}\)
![]() Can more than one formula from a piecewise function be applied to a value in the domain?
Can more than one formula from a piecewise function be applied to a value in the domain?
No. Each value corresponds to one equation in a piecewise formula.
Evaluating Piecewise Functions
When evaluating piecewise functions, the value in the domain determines the appropriate definition to use.
Example \(\PageIndex{7}\):
Given the function \(h\), find \(h(−5), h(0),\) and \(h(3)\).
\[h(t)= \begin{cases}
7t+5 & \text{if $t<0$} \\
-16t^2+32t &\text{if $t\geq 0$}
\end{cases} \nonumber \]
Solution
Use \(h(t) = 7t + 3\) where \(t\) is negative, as indicated by \(t < 0\).
\(\begin{aligned} h ( t ) & = 7 t + 5 \\ h ( \color{Cerulean}{- 5}\color{Black}{ )} & = 7 ( \color{Cerulean}{- 5}\color{Black}{)} + 5 \\ & = - 35 + 5 \\ & = - 30 \end{aligned}\)
Where \(t\) is greater than or equal to zero, use \(h(t) = −16t^{2} + 32t\).
\( \begin{array} {rlrl}
h ( \color{Cerulean}{0}\color{Black}{ )}
& = - 16 ( \color{Cerulean}{0}\color{Black}{ )} + 32 ( \color{Cerulean}{0}\color{Black}{ )}
& \qquad h ( \color{Cerulean}{3}\color{Black}{ )}
& = 16 ( \color{Cerulean}{3}\color{Black}{ )} ^ { 2 } + 32 ( \color{Cerulean}{3}\color{Black}{ )}
\\
& =0 + 0
&& = -144 +96
\\
& =0
&& =-48
\end{array} \)
Answer:
\(h(−5) = −30, h(0) = 0,\) and \(h(3) = −48\)
Example \(\PageIndex{8}\): Working with a Piecewise Function
A cell phone company uses the function below to determine the cost, \(C\), in dollars for \(g\) gigabytes of data transfer.
\[C(g)= \begin{cases} 25 & \text{if $0<g<2$} \\ 25+10(g-2) &\text{if $g\geq2$} \end{cases} \nonumber \]
Find the cost of using 1.5 gigabytes of data and the cost of using 4 gigabytes of data.
Solution
To find the cost of using 1.5 gigabytes of data, \(C(1.5)\), we first look to see which part of the domain our input falls in. Because 1.5 is less than 2, we use the first formula.
\[C(1.5)=$25 \nonumber \]
To find the cost of using 4 gigabytes of data, C(4), we see that our input of 4 is greater than 2, so we use the second formula.
\[C(4)=25+10(4−2)=$45 \nonumber \]
Analysis
The function is represented in Figure \(\PageIndex{8}\). We can see where the function changes from a constant to a shifted and stretched identity at \(g=2\). We plot the graphs for the different formulas on a common set of axes, making sure each formula is applied on its proper domain.
![[Graph of C(g)]](https://math.libretexts.org/@api/deki/files/895/CNX_Precalc_Figure_01_02_022.jpg?revision=1&size=bestfit&width=383&height=233)
The greatest Integer Function
The greatest integer function, denoted \(f(x) = {[{[ x ]}]} \) assigns the greatest integer less than or equal to any real number in its domain. For example,
\(\begin{aligned} f ( 2.7 ) & = {[{[ 2.7 ]}]} &= 2 \\ f ( \pi ) & = {[{[ \pi ]}]} &= 3 \\ f ( 0.23 ) & = {[{[0.23 ]}]} &= 0 \\ f ( - 3.5 ) & = {[{[ -3.5 ]}]} &= - 4 \end{aligned}\)
This function associates any real number with the greatest integer less than or equal to it and should not be confused with rounding off.
Example \(\PageIndex{9}\): Greatest Integer Function
Graph: \(f(x) = {[{[ x ]}]} \).
Solution
If \(x\) is any real number, then \(y = \) is the greatest integer less than or equal to \(x\).
\(\begin{aligned} \vdots\\- 1 \leq x < 0 & \color{Cerulean}{\Rightarrow}\color{Black}{ y} = {[{[ x ]}]}= -1 \\ 0 \leq x < 1 & \color{Cerulean}{\Rightarrow} \color{Black}{y} = {[{[ x ]}]}= 0 \\ 1 \leq x < 2 & \color{Cerulean}{\Rightarrow}\color{Black}{ y} = {[{[ x ]}]} = 1 \\ & \vdots \end{aligned}\)
Using this, we obtain the following graph.
Answer:
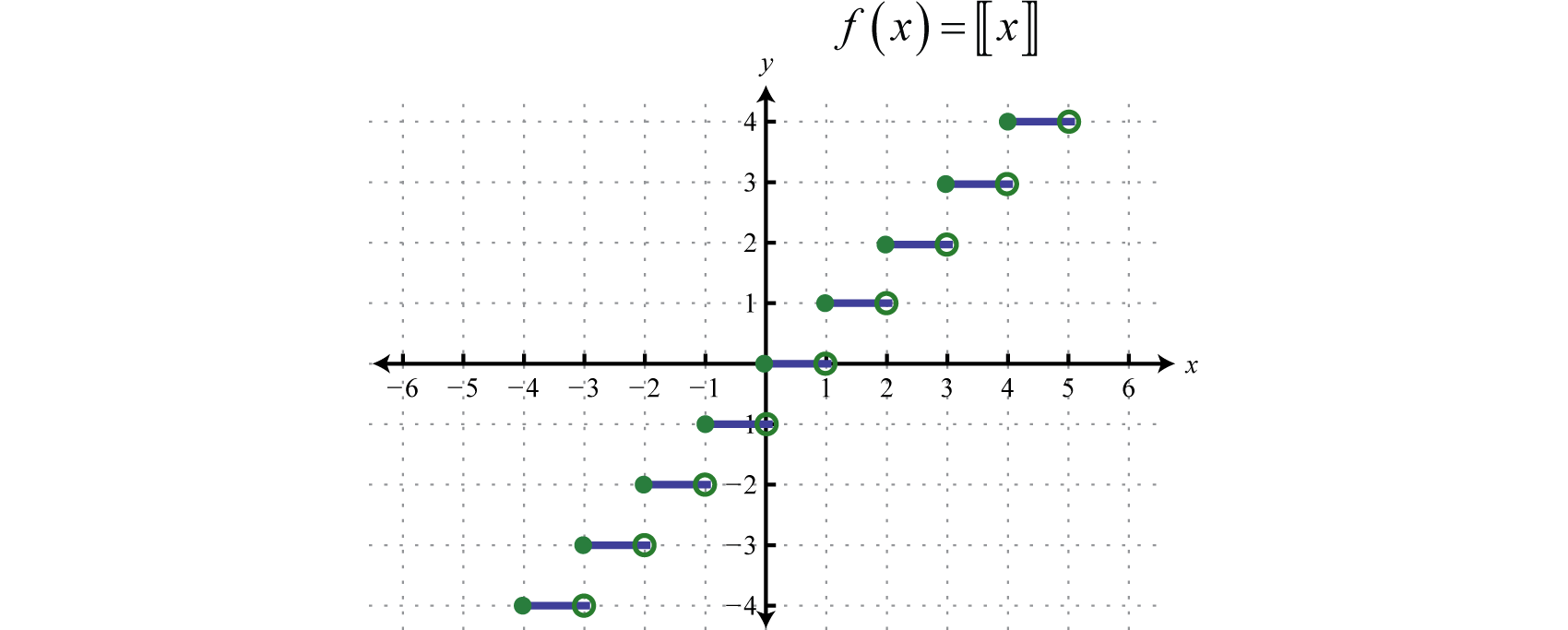
The domain of the greatest integer function consists of all real number \(\mathbb{R}\) and the range consists of the set of integers \(\mathbb{Z}\). This function is often called the floor function and has many applications in computer science.
Writing Piecewise-Defined Functions
![]() How to: Given a piecewise function, write the formula and identify the domain for each interval.
How to: Given a piecewise function, write the formula and identify the domain for each interval.
- Identify the intervals for which different rules apply.
- Determine formulas that describe how to calculate an output from an input in each interval.
- Use braces and if-statements to write the function.
Example \(\PageIndex{10}\): Writing a Piecewise Function
A museum charges $5 per person for a guided tour with a group of 1 to 9 people or a fixed $50 fee for a group of 10 or more people. Write a function relating the number of people, \(n\), to the cost, \(C\).
Solution
Two different formulas will be needed. For \(n\)-values under 10, \(C=5n\). For values of n that are 10 or greater, \(C=50\).
\[C(n)= \begin{cases} 5n & \text{if $n < 10$} \\ 50 &\text{if $n\geq10$} \end{cases} \nonumber \]
Analysis
The function is represented in Figure \(\PageIndex{10}\). The graph is a diagonal line from \(n=0\) to \(n=10\) and a constant after that. In this example, the two formulas agree at the meeting point where \(n=10\), but not all piecewise functions have this property.
![[Graph of C(n).]](https://math.libretexts.org/@api/deki/files/894/CNX_Precalc_Figure_01_02_021.jpg?revision=1&size=bestfit&width=285&height=233)
Example \(\PageIndex{11}\): Writing a Greatest Integer Piecewise-Defined Function
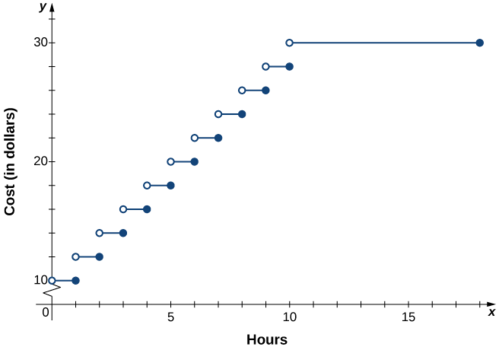
In a big city, drivers are charged variable rates for parking in a parking garage. They are charged $10 for the first hour or any part of the first hour and an additional $2 for each hour or part thereof up to a maximum of $30 for the day. The parking garage is open from 6 a.m. to 12 midnight.
- Write a piecewise-defined function that describes the cost \(C\) to park in the parking garage as a function of hours parked \(x\).
- Sketch a graph of this function \(C(x).\)
Solution
1.Since the parking garage is open 18 hours each day, the domain for this function is \( \{ x \;|\; 0 < x ≤ 18 \} \). The cost to park a car at this parking garage can be described piecewise by the function
\[C(x)=\begin{cases}
10, & 0 < x ≤ 1 \\
12, & 1<x≤2\\
14, & 2<x≤3\\
16, & 3<x≤4\\
⋮\\
30, & 10<x≤18\end{cases}. \nonumber \]
2.The graph of the function consists of several horizontal line segments.
![]() Try It \(\PageIndex{12}\)
Try It \(\PageIndex{12}\)
The cost of mailing a letter is a function of the weight of the letter. Suppose the cost of mailing a letter is \(49¢\) for the first ounce and \(21¢\) for each additional ounce. Write a piecewise-defined function describing the cost \(C\) as a function of the weight \(x\) for \(0<x≤3\), where \(C\) is measured in cents and \(x\) is measured in ounces.
- Hint
-
The piecewise-defined function is constant on the intervals (0,1], (1,2],….
- Answer
-
\[C(x)=\begin{cases}49, &0<x≤1\\70, &1<x≤2\\91, &2<x≤3\end{cases} \nonumber \]
Algebraic Combinations of Functions
Functions have their own arithmetic which is consistent with the arithmetic of real numbers. The following definitions allow us to add, subtract, multiply and divide functions using the arithmetic we already know for real numbers.
Definition: Function Arithmetic
Suppose \(f\) and \(g\) are functions and \(x\) is in both the domain of \(f\) and the domain of \(g\). The domain of the combination function is the intersection of the two domains.
- The sum of \(f\) and \(g\), denoted \(f+g\), is the function defined by the formula \[(f+g)(x) = f(x) + g(x) \nonumber \]
- The difference of \(f\) and \(g\), denoted \(f-g\), is the function defined by the formula \[(f-g)(x) = f(x) - g(x) \nonumber \]
- The product of \(f\) and \(g\), denoted \(fg\), is the function defined by the formula \[(fg)(x) = f(x) \cdot g(x) \nonumber \]
- The quotient of \(f\) and \(g\), denoted \(\dfrac{f}{g}\), is the function defined by the formula \[\left(\dfrac{f}{g}\right)(x) = \dfrac{f(x)}{g(x)}, \qquad \text{ provided } g(x) \neq 0 \nonumber \]
In other words, to add two functions, we add their outputs; to subtract two functions, we subtract their outputs, and so on. Note that while the formula \((f+g)(x) = f(x) + g(x)\) looks suspiciously like some kind of distributive property, it is nothing of the sort; the addition on the left hand side of the equation is function addition, and we are using this equation to define the output of the new function \(f+g\) as the sum of the real number outputs from \(f\) and \(g\).
![]() How to: Find a Combination Function and its Domain.
How to: Find a Combination Function and its Domain.
- Write the formula for the combination function.
- Substitute the given functions.
- Use this UN-simplified expression to find the domain of the combination function.
- Simplify the expression. If in the simplification process, a factor like for example (\(x-c)\) is canceled, then the final result should also include a statement like \( ... , x \neq c \), indicating the restriction to the combination function that is no longer apparent in its formula .
Example \(\PageIndex{13}\): Performing Algebraic Operations on Functions
Given \(f(x)=x−1\) and \(g(x)=x^2−1\). Determine the compound function, simplify the result, and find the domain of the compound function.
- \((g−f)(x)\)
- \(\left(\dfrac{g}{f}\right)(x)\)
Solution. Begin by writing the formula for the combination function, and then substitute the given functions.
\(\begin{align*}a. \quad (g−f)(x) &= g(x)−f(x) \\[4pt] &=(x^2−1)−(x−1) && \text{This expression has no domain restrictions}\\[4pt]
&=x^2−x &&\text{Now simplify}\\[4pt] (g−f)(x)&=x(x−1) \end{align*}\)
The domain of \((g−f)(x)\) is \( ( -\infty, \infty ) \)
\(\begin{align*} b. \quad \left(\dfrac{g}{f}\right)(x)&= \dfrac{g(x)}{f(x)} \\[4pt]
&=\dfrac{x^2−1}{x−1} && \text{This expression the domain restriction } x \ne 1 \\[4pt]
&=\dfrac{(x+1)(x−1)}{x−1} &&\text{Now simplify}\\[4pt]
\left(\dfrac{g}{f}\right)(x)&=x+1, \quad x \ne 1 \end{align*}\)
The domain of \(\left(\dfrac{g}{f}\right)(x)\) is \( ( -\infty,1) \cup (1, \infty ) \). Note: For \(\left(\dfrac{g}{f}\right)(x)\), the condition \(x\neq1\) is necessary because when \(x=1\), and the compound function is constructed from the beginning, the denominator is equal to 0, which makes the function undefined.
![]() Try It \(\PageIndex{14}\)
Try It \(\PageIndex{14}\)
Given \( f(x)=x−1 \) and \(g(x)=x^2−1 \) Find and simplify the functions below and determine their domain.
- \((fg)(x)\)
- \((f−g)(x)\)
- Answer
-
a. \((fg)(x)=f(x)g(x)=(x−1)(x^2−1)=x^3−x^2−x+1 \qquad \) Domain is \( ( -\infty, \infty ) \)
b. \((f−g)(x)=f(x)−g(x)=(x−1)−(x^2−1)=x−x^2 \qquad \) Domain is \( ( -\infty, \infty ) \)
Example \(\PageIndex{15}\):
Let \(f(x) = 6x^2 - 2x\) and \(g(x) = 3-\dfrac{1}{x}\).
- Find \((f+g)(-1)\)
- Find \((fg)(2)\)
- Find the domain of \(g-f\) then find and simplify a formula for \((g-f)(x)\).
- Find the domain of \(\left(\dfrac{g}{f}\right)\) then find and simplify a formula for \(\left(\frac{g}{f}\right)(x)\).
Solution
- To find \((f+g)(-1)\) we first find \(f(-1) = 8\) and \(g(-1) = 4\). By definition, we have that \((f+g)(-1) = f(-1) + g(-1) = 8+4 = 12.\)
- To find \((fg)(2)\), we first need \(f(2)\) and \(g(2)\). Since \(f(2) = 20\) and \(g(2) = \frac{5}{2}\), our formula yields \((fg)(2) = f(2) \cdot g(2) = (20)\left(\frac{5}{2}\right) = 50.\)
- To find the domain of \(g-f\) the formula for \((g-f)(x)\) needs to be analyzed before simplifying. Because \(x\) is in the denominator, \(x\) cannot be \(0\).
\( (g-f)(x) = g(x) - f(x) = \left(3-\dfrac{1}{x}\right) - \left(6x^2 - 2x\right)\)
So the domain is \((-\infty, 0) \cup (0, \infty)\).
Next, the formula for \((g-f)(x)\) must be simplified. In this case, we get common denominators and attempt to reduce the resulting fraction. Doing so, we get
\( \begin{array}{rclr} (g-f)(x) & = & g(x) - f(x) & \\[5pt]
& = & \left(3-\dfrac{1}{x}\right) - \left(6x^2 - 2x\right) = 3 - \dfrac{1}{x} - 6x^2 + 2x & \\[5pt]
& = & \dfrac{3x}{x} - \dfrac{1}{x} - \dfrac{6x^3}{x} + \dfrac{2x^2}{x} & \text{get common denominators} \\
& = & \dfrac{3x - 1 - 6x^3 + 2x^2}{x} = \dfrac{-6x^3 + 2x^2 +3x-1}{x} & \\
& = & \dfrac{-2x^2(3x-1)+1(3x-1)}{x} = \dfrac{(3x-1)(-2x^2+1)}{x} & \\
& = & \dfrac{-(3x-1)(2x^2-1)}{x} & \\
\end{array}\)
d. As in the previous example, write the formula, substitute the values of the functions and then examine the un-simplified result to determine the domain of the combination function.
\( \left(\dfrac{g}{f}\right)(x) = \dfrac{g(x)}{f(x)} = \dfrac{3-\dfrac{1}{x}\vphantom{\left(\dfrac{1}{x}\right)}}{6x^2 - 2x}\)
We see immediately from the 'little' denominator that \(x \neq 0\). To keep the 'big' denominator away from \(0\), we solve \(6x^2 - 2x = 0,\) or \(2x(3x-1)=0,\) and get \(x = 0\) or \(x = \frac{1}{3}\). Hence, as before, we find the domain of \(\dfrac{g}{f}\) to be \((-\infty, 0) \cup \left(0, \frac{1}{3}\right) \cup \left(\frac{1}{3}, \infty\right)\).
Next, the formula for \(\left(\dfrac{g}{f}\right)(x)\) must be simplified.
\( \begin{array}{rll}
\left(\dfrac{g}{f}\right)(x) &=\cfrac{ \left( 3-\cfrac{1}{x} \right)} {2x(3x - 1)} \cdot \cfrac{ \cfrac{x}{1} }{x/1} & \text{factor and clear complex fraction} \\[5pt]
&= \dfrac{3x-1}{2x^2(3x - 1)} = \dfrac{1}{2x^2} \\
\end{array}\)
Our final answer then is \(\left(\dfrac{g}{f}\right)(x) = \dfrac{1}{2x^2}, \quad x \ne \frac{1}{3}\) and the domain is \((-\infty, 0) \cup \left(0, \frac{1}{3}\right) \cup \left(\frac{1}{3}, \infty\right)\).
Please note the importance of finding the domain of a function before simplifying its expression. If we waited to find the domain of \(\dfrac{g}{f}\) until after simplifying, we'd just have the formula \(\frac{1}{2x^2}\) to go by, and we would (incorrectly!) state the domain as \((-\infty, 0) \cup (0,\infty)\), since the other troublesome number, \(x = \frac{1}{3}\), was canceled away.
Composition of Functions
Suppose we wanted to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and the average daily temperature depends on the particular day of the year. Notice how we have just defined two relationships: The cost depends on the temperature, and the temperature depends on the day. Using descriptive variables, we can notate these two functions.
The first function, \(C(T)\), gives the cost \(C\) of heating a house when the average daily temperature is \(T\) degrees Celsius, and the second, \(T(d)\), gives the average daily temperature on day \(d\) of the year in some city. If we wanted to determine the cost of heating the house on the \(5^{th}\) day of the year, we could do this by linking our two functions together, an idea called composition of functions. Using the function \(T(d)\), we could evaluate \(T(5)\) to determine the average daily temperature on the 5 \({}^{th}\) day of the year. We could then use that temperature as the input to the \(C(T)\) function to find the cost to heat the house on the 5 \({}^{th}\) day of the year: \(C(T(5))\).
Definition: Composition of Functions
The composition of the function \(f\) with \(g\) is denoted by \((f \circ g)(x)\), read “\(f\) of \(g\) of \(x\)”, and is defined by the equation
\((f \circ g)(x) = f(g(x))\)
In general, \(f{\circ}g\) and \(g{\circ}f\) are different functions.
It is important to realize that the product of functions \((fg)(x)\) is not the same as the function composition \((f \circ g)(x) \).
The domain of the composite function \(f \circ g\) is the set of all \(x\) such that
- \(x\) is in the domain of \(g\) and \( \qquad \qquad \leftarrow\) so that the first (inner) operation is defined
- \(g(x)\) is in the domain of \(f\). \( \qquad \qquad \leftarrow\) so that the final resulting operation is defined
Example \(\PageIndex{16}\): Interpreting Composite Functions
The function \(c(s)\) gives the number of calories burned completing \(s\) sit-ups, and \(s(t)\) gives the number of sit-ups a person can complete in \(t\) minutes. Interpret \(c(s(3))\).
Solution
The inside expression in the composition is \(s(3)\). Because the input to the \(s\)-function is time, \(t=3\) represents 3 minutes, and \(s(3)\) is the number of sit-ups completed in 3 minutes.
Using \(s(3)\) as the input to the function \(c(s)\) gives us the number of calories burned during the number of sit-ups that can be completed in 3 minutes, or simply the number of calories burned in 3 minutes (by doing sit-ups).
Note that it is not important that the same variable be used for the output of the inside function and the input to the outside function. However, it is essential that the units on the output of the inside function match the units on the input to the outside function, if the units are specified.
Example \(\PageIndex{17}\): Investigating the Order of Function Composition
Suppose \(f(x)\) gives miles that can be driven in \(x\) hours and \(g(y)\) gives the gallons of gas used in driving \(y\) miles. Which of these expressions is meaningful: \(f(g(y))\) or \(g(f(x))\)?
Solution
The function \(y=f(x)\) is a function that produces the number of miles driven given the number of hours driven:
\[\text{number of miles } =f (\text{number of hours}) \nonumber\]
The function \(g(y)\) is a function that produces the number of gallons used given the number of miles driven:
\[\text{number of gallons } =g(\text{number of miles}) \nonumber\]
Consider the composition \(f(g(y))\). The expression \(g(y)\) takes miles as the input and a number of gallons as the output. The function \(f(x)\) requires a number of hours as the input. Trying to input a number of gallons into \(f\) does not make sense. The expression \(f(g(y))\) is meaningless.
Consider the composition \(g(f(x))\). The expression \(f(x)\) takes hours as input and a number of miles driven as the output. The function \(g(y)\) requires a number of miles as the input. Using \(f(x)\) (miles driven) as an input value for \(g(y)\), where gallons of gas depends on miles driven, does make sense. The expression \(g(f(x))\) makes sense, and will yield the number of gallons of gas used, \(g\), driving a certain number of miles, \(f(x)\), in \(x\) hours.
![]() Try It \(\PageIndex{18}\)
Try It \(\PageIndex{18}\)
In a department store you see a sign that says 50% off clearance merchandise, so final cost \(C\) depends on the clearance price, \(p\), according to the function \(C(p)\). Clearance price, \(p\), depends on the original discount, \(d\), given to the clearance item, \(p(d)\). Interpret \(C(p(d))\).
- Answer
-
The final cost, \(C\), depends on the clearance price, \(p\), which is based on the original discount, \(d\). (Or the original discount \(d\), determines the clearance price and the final cost is half of the clearance price.)
![]() Try It \(\PageIndex{19}\)
Try It \(\PageIndex{19}\)
The gravitational force on a planet a distance \(r\) from the sun is given by the function \(G(r)\). The acceleration of a planet subjected to any force \(F\) is given by the function \(a(F)\). Form a meaningful composition of these two functions, and explain what it means.
- Answer
-
A gravitational force is still a force, so \(a(G(r))\) makes sense as the acceleration of a planet at a distance \(r\) from the Sun (due to gravity), but \(G(a(F))\) does not make sense.
Evaluating Composite Functions
When working with functions given as tables, graphs, and formulas we can look up values for the functions using a provided table, graph, or formula. Start evaluation with the inside function. Then use the output of the inside function as the input to the outside function. To remember this, always work from the inside out - just like with order of operations.
Evaluate Composite Functions Using Tables
When working with functions given as tables, we read input and output values from the table entries and always work from the inside to the outside. We evaluate the inside function first and then use the output of the inside function as the input to the outside function.
Example \(\PageIndex{20}\): Using a Table to Evaluate a Composite Function
|
Using the tables below, evaluate \(f(g(3))\) and \(g(f(3))\).
|
Solution To evaluate \(f(g(3)),\) start from the inside with the input value 3. Then evaluate the inside expression \(g(3)\) using the table that defines the function \(g: g(3)=2\). Use that result as the input to the function \(f\), so \(g(3)\) is replaced by 2 to get \(f(2)\). Then, using the table that defines the function \(f\), we find that \(f(2)=8\). Step \(1: \; g(3)=2, \quad\) Step \(2: \; f(g(3))=f(2)=8\) To evaluate \(g(f(3)),\) first evaluate the inside expression \(f(3)\) using the first table: \(f(3)=3\). Then, using the table for \(g\), we can evaluate Step \(1: \; f(3)=3, \quad\) Step \(2: \; g(f(3))=g(3)=2\) |
![]() Try It \(\PageIndex{21}\)
Try It \(\PageIndex{21}\)
Use the table in Example \(\PageIndex{20}\) above to evaluate \(f(g(1))\), \(g(f(4))\) and \(f(g(4))\).
- Answer
-
\(f(g(1))=f(3)=3\), \(g(f(4))=g(1)=3\), and \(f(g(4)) = f(7) = \text{undefined}\)
Notice the composition is not a commutative operation!
Evaluate Composite Functions Using Graphs
When we are given individual functions as graphs, the procedure for evaluating composite functions is similar to the process we use for evaluating tables. We read the input and output values, but this time, from the \(x\)- and \(y\)-axes of the graphs.
![]() How to: Use graphs of individual functions to evaluate a composite function.
How to: Use graphs of individual functions to evaluate a composite function.
- Locate the given input to the inner function on the \(x\)-axis of its graph.
Read off the output of the inner function from the \(y\)-axis of its graph. - Locate the inner function output on the \(x\)-axis of the graph of the outer function.
Read the output of the outer function from the \(y\)-axis of its graph. This is the output of the composite function.
Example \(\PageIndex{22}\): Using a Graph to Evaluate a Composite Function
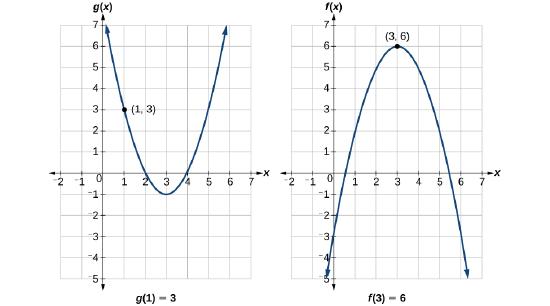
Using Figure \(\PageIndex{22}\), evaluate \(f(g(1))\).
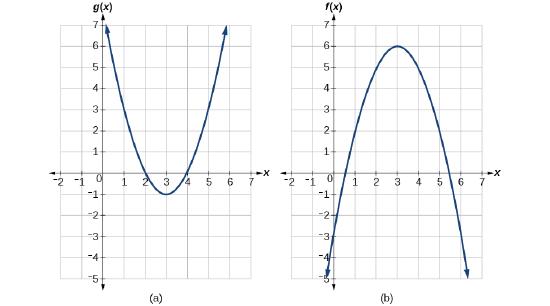
Solution
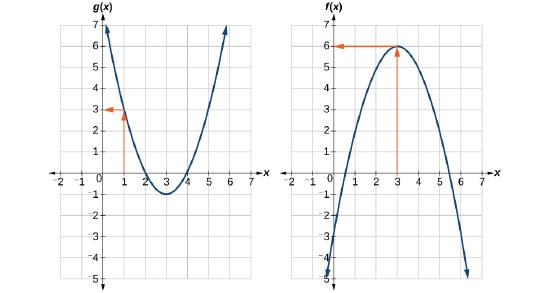
To evaluate \(f(g(1))\), we start with the inside evaluation. See Figure \(\PageIndex{22}\).
Step 1. \(f(g(1))=f(3)\): We evaluate \(g(1)\) using the graph of \(g(x)\), finding the input of 1 on the x-axis and finding the output value of the graph at that input. Here, \(g(1)=3\). We use this value as the input to the function \(f\).
Step 2. \(f(3)=6\): We can then evaluate the composite function by looking to the graph of \(f(x)\), finding the input of 3 on the x-axis and reading the output value of the graph at this input. Here, \(f(3)=6\), so \(f(g(1))=6\).
|
|
![]() Try It \(\PageIndex{23}\)
Try It \(\PageIndex{23}\)
Using Figure \(\PageIndex{22}\), evaluate \(g(f(2))\).
- Answer
-
\(g(f(2))=g(5)=3\)
Evaluate Composite Functions Using Formulas
When evaluating a composite function where we have either created or been given formulas, the rule of working from the inside out remains the same. The input value to the outer function will be the output of the inner function, which may be a numerical value, a variable name, or a more complicated expression.
![]() How to: Evaluate a Composition \( (f \circ g)(c) \).
How to: Evaluate a Composition \( (f \circ g)(c) \).
- Write the definition for the composition function: \((f \circ g)(c) = f(g(c)) \).
- Substitute \(c\) in the function definition for \(g\) to evaluate the inside function \(g(c)\). Let \(k\) be this result: \((f \circ g)(c) = f(g(c))=f(k) \).
- Substitute \(k\) in the function definition for \(f\) to evaluate the outside function
Example \(\PageIndex{24}\): Evaluate a Composition of Functions Expressed as Formulas with a Numerical Input
Given \(f(t)=t^2−t\) and \(h(x)=3x+2\), evaluate \( (f \circ h)(1))\).
Solution
Rewrite \( (f \circ h)(1))\) using the definition: \( (f \circ h)(1)) = f(h(1))\)
The inside expression is \(h(1)\). The argument of \(h\) is \(1\), so substitute \(1\) for \(x\) in the formula for \(h\) and evaluate it.
\[ \begin{align*} h(1)&=3(1)+2 \\[4pt] h(1)&=5 \end{align*} \]
Now \(f(h(1))=f(5)\). The argument of \(f\) is \(5\) so substitute \(5\) for \(t\) in the formula for \(f\) and evaluate it.
\[ \begin{align*} f(h(1)) &=f(5) \\[5pt] f(h(1))&=5^2−5 \\[5pt] f(h(1))&=20 \end{align*} \]
Analysis
It makes no difference what the input variables \(t\) and \(x\) were called in this problem because we evaluated for specific numerical values.
Example \(\PageIndex{25}\): Evaluating a Composition of Functions Expressed as Formulas with a Numerical Input
Given \(f(x) = x^2-4x\), \(g(x) = 2-\sqrt{x+3}\), and \(h(x) = \dfrac{2x}{x+1}\) evaluate the following.
- \((g \circ f)(1) \qquad \) b. \((f \circ g)(1) \qquad \) c. \((g \circ g)(6) \qquad \) d. \((g \circ f)(2) \qquad \) e. \((g \circ h)(-1) \qquad \)
Solution
a. Use the definition: \((g \circ f)(1) = g(f(1))\).
\(\quad\) Evaluate the inner function: \(f(1) = -3\)
\(\quad\) Evaluate the outer function using this result: \( g(f(1)) = g(-3) = 2 \)
b. Use the definition to write \((f \circ g)(1) = f(g(1))\).
\(\quad\) Evaluate the inner function: \(g(1) = 0\),
\(\quad\) Evaluate the outer function using this result: \(f(g(1)) = f(0) = 0 \)
c. Use the definition \((g \circ g)(6) = g(g(6))\).
\(\quad\) Evaluate the inner function: \(g(6) = -1\)
\(\quad\) Evaluate the outer function using this result: \( g(g(6)) = g(-1) = 2-\sqrt{2} \)
d. Use the definition: \((g \circ f)(2) = g(f(2))\)
\(\quad\) Evaluate the inner function: \(f(2) = (2)^2-4(2)=4-8=-4\)
\(\quad\) Evaluate the outer function using this result: \(g(f(2)) = g(-4) = 2-\sqrt{-4+3} =2-\sqrt{-1} = 2-i\). This result is not a real number, so we say \((g \circ f)(2) \) is undefined.
e. Use the definition: \((g \circ h)(-1) = g(h(-1))\)
\(\quad\) Evaluate the inner function: \(h(-1) = \dfrac{2(-1)}{(-1)+1}= \dfrac{-2}{0} = \text{undefined}\)
\(\quad\) Evaluate the outer function: \( g(h(-1)) =g(\text{undefined}) \) cannot be evaluated! So \((g \circ h)(-1) = \text{undefined}\).
![]() Try It \(\PageIndex{26}\)
Try It \(\PageIndex{26}\)
Given \(f(t)=t^2−t\) and \(h(x)=3x+2\), evaluate
a. \(h(f(2))\)
b. \(h(f(−2))\)
- Answers:
-
a. 8 \( \qquad \) b. 20
Finding the Formula and Domain of a Composite Function
While we can compose the functions for each individual input value, it is sometimes helpful to find a single formula that will calculate the result of a composition \((f \circ g)(x)\). To do this, we will extend our idea of function evaluation. Recall that, when we evaluate a function with a formula like \(f(t)=t^2−t\), we substitute the value inside the parentheses (called the argument) into the formula wherever we see the input variable.
The domain of a composite function such as \(f{\circ}g\) is dependent on the domain of \(g\) and the domain of \(f\). It is important to know when we can apply a composite function and when we cannot, that is, to know the domain of a function such as \(f{\circ}g\). If we write the composite function for an input \(x\) as \(f(g(x))\), we can see right away that \(x\) must be a member of the domain of \(g\) in order for the expression to be meaningful, because otherwise we cannot complete the inner function evaluation. Secondly, the outer function evaluation, \(f(g(x))\), must also be defined. Thus the restrictions to the domain of \(f{\circ}g\) consist of not only the values of \(x\) that make \(g(x)\) undefined, but also the values of \(x\) that make the expression \(f(g(x))\) undefined.
![]() How to: Determine a Function Composition \( (f \circ g)(x) \) and its Domain.
How to: Determine a Function Composition \( (f \circ g)(x) \) and its Domain.
- Write the definition for the composition function: \((f \circ g)(x) = f(g(x)) \).
- Substitute the function definition for \(g\) in for the argument of \(f\).
Determine the domain of \(g\) because the argument to \(f\) must be defined during the composition process. - Substitute the argument expression \(g(x)\) into the function definition for \(f\) to determine the formula for \((f \circ g)(x)\).
- Simplify the formula for \((f \circ g)(x)\).
- The domain of \((f \circ g)(x)\) combines both the domain restrictions to the inner function and the domain restrictions apparent in the resulting function. It is important to include the domain restrictions to \(g\) because sometimes they get lost in the simplification process (step 4).
Example \(\PageIndex{27}\): Finding a composition and its domain
Given \(f(x)=5x−1 \) and \( g(x)=\dfrac{4}{3x−2}\) find \((f∘g)(x)\) and its domain.
Solution: 1. \((f∘g)(x) = f(g(x))\)
2. \(f(g(x)) = f \Big(\dfrac{4}{3x−2} \Big) \). The domain of \(g(x)\) consists of all real numbers except \(x=\frac{2}{3}\), since that input value would cause us to divide by 0.
3. \( f \Big(\dfrac{4}{3x−2} \Big) = 5\Big(\dfrac{4}{3x−2} \Big) -1 \). Notice in this form the domain restriction \(x \ne \frac{2}{3}\)
4. \(5\Big(\dfrac{4}{3x−2} \Big) -1 = 5\Big(\dfrac{4}{3x−2} \Big) - \dfrac{3x−2}{3x−2} = \dfrac{20 -3x+2}{3x−2} =\dfrac{22-3x}{3x−2} \)
5. The domain restriction of the simplified expression is still \(x \ne \frac{2}{3}\).
Answer: \((f∘g)(x) = \dfrac{22-3x}{3x−2}\) and its domain is \( (−\infty,\dfrac{2}{3}) \cup (\dfrac{2}{3},\infty) \)
Example \(\PageIndex{28}\)
Given \(f(x)=\sqrt{x+2}\) and \(g(x)=\sqrt{3−x}\) find \((f∘g)(x)\) and its domain.
Solution: 1. \((f∘g)(x) = f(g(x))\)
2. \(f(g(x)) = f (\sqrt{3−x})\). The domain restriction for \(g\) is \(3-x \ge 0 \longrightarrow 3 \ge x \longrightarrow x \le 3\)
3. \(f (\sqrt{3−x})= \sqrt{\sqrt{3−x}+2}\)
4. This expression cannot be simplified.
5. The domain restriction for this expression is \(\sqrt{3−x}+2 \ge 0\). As long as \(\sqrt{3-x}\) is a real number, \(\sqrt{3−x} \ge 0\) so \(\sqrt{3−x}+2 \ge 2\). The expression \(\sqrt{3-x}\) is a real number whenever \(3-x \ge 0\) or \(x \le 3\).
Answer: \((f∘g)(x)=\sqrt{ \sqrt{3−x}+2}\) and its domain is \((-∞,3]\).
Example \(\PageIndex{29}\)
Let \(f(x) = x^2-4x\), \(g(x) = 2-\sqrt{x+3}\), and \(h(x) = \dfrac{2x}{x+1}\). Find and simplify the indicated composite functions. State the domain of each.
- \((f \circ g)(x)\)
- \((h \circ g)(x)\)
- \((h \circ h)(x)\)
Solution
a. \(\quad \;\)1. \((f \circ g)(x)= f(g(x))\)
2. \(f(g(x)) = f(2-\sqrt{x+3})\). The domain of \(g\) is \( x+3 \ge 0 \longrightarrow x \ge -3\)
\( \begin{array}{rrll}
3.& f(2-\sqrt{x+3}) &= (2-\sqrt{x+3})^2 - 4(2-\sqrt{x+3}) \\
4.& &= 4 - 4 \sqrt{x+3} + (\sqrt{x+3})^2 - 8 + 4\sqrt{x+3} \\
&&= 4 + x + 3 - 8\\
&&= x-1
\end{array}\)
5. The resulting expression has no domain restrictions, but the domain restriction found for \(g\) still applies to the composition process.
Answer: \((f \circ g)(x)= x-1\) with a domain of \([-3, \infty)\)
b. \(\quad \;\)1. \((h \circ g)(x) = h(g(x))\)
2. \(h(g(x)) = h (2-\sqrt{x+3})\). The domain of \(g\) here is \(x+3 \ge 0 \longrightarrow x \ge -3\).
\( \begin{array}{rrll}
3.& h (2-\sqrt{x+3})&=\dfrac{2(2-\sqrt{x+3})}{(2-\sqrt{x+3})+1} \\
4.& &= \dfrac{4-2\sqrt{x+3}}{3-\sqrt{x+3}} &\text{Simplify} \\
& &= \dfrac{4-2\sqrt{x+3}}{3-\sqrt{x+3}}\cdot \dfrac{3+\sqrt{x+3}}{3+\sqrt{x+3}} &\text{Rationalize denominator} \\
& &= \dfrac{12+4\sqrt{x+3}-6\sqrt{x+3}-2(x+3)}{9-(x+3)} &\text{Multiply out and simplify} \\
& &= \dfrac{6-2x-2\sqrt{x+3}}{6-x} \\
\end{array}\)
5. The resulting expression has two domain restrictions: \(x+3 \ge 0 \) and \( 6-x \ne 0 \). Therefore, \(x \ge -3\) and \(x \ne 6\). Both of these restrictions apply to the composition process. The domain restriction to \(g\) found earlier is repeated here.
Answer: \((h \circ g)(x) = = \dfrac{4-2\sqrt{x+3}}{3-\sqrt{x+3}}\) with a domain of \([-3,6) \cup (6, \infty)\).
c. \(\quad \;\)1. \((h \circ h)(x) = h(h(x))\).
2. \( h(h(x)) = h \Big( \dfrac{2x}{x+1}\Big) \). The domain of \(h\) here is \(x + 1 \ne 0 \longrightarrow x \ne -1\).
\(\begin{array}{rrll}
3. & h \left( \dfrac{2x}{x+1} \right) &= \dfrac{2\Big( \dfrac{2x}{x+1} \Big)}{\Big( \dfrac{2x}{x+1} \Big) + 1 }\\
\end{array}\)
\(\begin{array}{rrll}
4.& \qquad \qquad \qquad \qquad &= \dfrac{ \Big( \dfrac{4x}{x+1} \Big)}{\Big( \dfrac{2x}{x+1} \Big) + 1 }\cdot \dfrac{x+1}{x+1} &\text{Simplify complex fraction}\\
&&= \dfrac{ \Big( \dfrac{4x}{x+1} \Big) \cdot (x+1)}{\Big( \dfrac{2x}{x+1} \Big)\cdot (x+1) + 1\cdot (x+1) }\\
&&= \dfrac{4x}{2x+x+1} = \dfrac{4x}{3x+1}
\end{array}\)
5. The resulting expression has one domain restriction, \( 3x+1 \ne 0\). Therefore, \(x \ne \frac{1}{3}\). The domain of the composition process includes not only this domain but also the domain restriction to \(h\) found earlier: \(x \ne -1\)
Answer: \((h \circ h)(x) =\dfrac{4x}{3x+1}\) and its domain is \((-\infty, -1) \cup \left(-1, -\frac{1}{3}\right) \cup \left(-\frac{1}{3}, \infty\right)\).
![]() Try It \(\PageIndex{30}\)
Try It \(\PageIndex{30}\)
Find and simplify \((f∘g)(x)\) and find its domain given
- \(f(x)=\dfrac{1}{x−2} \text{ and } g(x)=\sqrt{x+4}\)
- \( f(x)=\dfrac{4}{3x−2}\) and \(g(x)=\dfrac{1}{x-1}\)
- Answers
-
a. \((f∘g)(x) = \dfrac{2+\sqrt{x+4}}{x}\) with domain \([−4,0)∪(0,∞)\) \(\qquad\) b. \((f∘g)(x) = \dfrac{4(x-1)}{5-2x}\) with domain \((-∞, 1)∪(1, 2.5)∪(2.5,∞)\)
Decomposing a Composite Function into its Component Functions
In some cases, it is necessary to decompose a complicated function. In other words, we can write it as a composition of two simpler functions. There may be more than one way to decompose a composite function, so we may choose the decomposition that appears to be most expedient.
Example \(\PageIndex{31}\): Decomposing a Function
Write \(f(x)=\sqrt{5−x^2}\) as the composition of two functions.
Solution
We are looking for two functions, \(g\) and \(h\), so \(f(x)=g(h(x))\). To do this, we look for a function inside a function in the formula for \(f(x)\). As one possibility, we might notice that the expression \(5−x^2\) is the inside of the square root. We could then decompose the function as
\(h(x)=5−x^2 \text{ and } g(x)=\sqrt{x}\)
We can check our answer by recomposing the functions.
\(g(h(x))=g(5−x^2)=\sqrt{5−x^2}\)
![]() Try It \(\PageIndex{32}\)
Try It \(\PageIndex{32}\)
Write \(f(x)=\dfrac{4}{3−\sqrt{4+x^2}}\) as the composition of two functions.
- Answer
-
Possible answers:
\(g(x)=\sqrt{4+x^2}\)
\(h(x)=\dfrac{4}{3−x}\)
\(f=h{\circ}g\)

