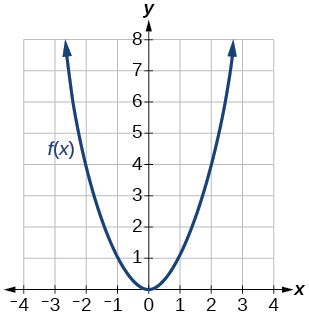
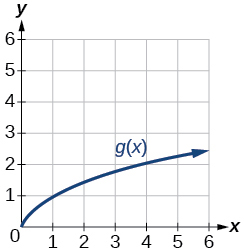
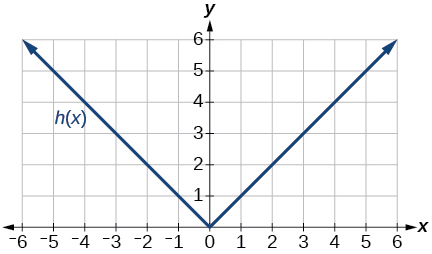
2.4e: Exercises - Piecewise Functions, Combinations, Composition
- Page ID
- 49550
A: Concepts
Exercise \(\PageIndex{A}\)
1) How does one find the domain of the quotient of two functions, \(\dfrac{f}{g}\)?
2) What is the composition of two functions, \(f{\circ}g\)?
3) If the order is reversed when composing two functions, can the result ever be the same as the answer in the original order of the composition? If yes, give an example. If no, explain why not.
4) How do you find the domain for the composition of two functions, \(f{\circ}g\)?
5) How do you graph a piecewise function?
- Answers 1-5:
-
1. Find the numbers that make the function in the denominator \(g\) equal to zero, and check for any other domain restrictions on \(f\) and \(g\), such as an even-indexed root or zeros in the denominator
3. Yes. Sample answer: Let \(f(x)=x+1\) and \(g(x)=x−1\). Then \(f(g(x))=f(x−1)=(x−1)+1=x\) and \(g(f(x))=g(x+1)=(x+1)−1=x\). So \(f{\circ}g=g{\circ}f\).
5. Graph each formula of the piecewise function over its corresponding domain. Use the same scale for the x-axis and y-axis for each graph. Indicate inclusive endpoints with a solid circle and exclusive endpoints with an open circle. Use an arrow to indicate endpoints of −∞ or ∞.Combine the graphs to find the graph of the piecewise function
Piecewise Functions
B. Evaluate Piecewise Functions
Exercise \(\PageIndex{B}\)
Given function \(f\), evaluate \(f(−3)\), \(f(−2)\), \(f(−1)\), and \(f(0)\).
| 6. \(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\) | 7. \(f(x)= \begin{cases} 1 & \text{if $x \leq -3$} \\ 0 & \text{if $x > -3$} \end{cases}\) | 8. \(f(x)= \begin{cases} -2x^2+3 & \text{if $x \leq -1$} \\ 5x-7 & \text{if $x > -1$} \end{cases}\) |
Given function \(f\), evaluate \(f(−1)\), \(f(0)\), \(f(2)\), and \(f(4)\).
| 9. \(f(x)= \begin{cases} 7x+3 & \text{if $x < 0$} \\ 7x+6 & \text{if $x {\geq} 0$} \end{cases}\) | 10. \(f(x)= \begin{cases} x^2-2 & \text{if $x < 2$} \\ 4+|x-5| & \text{if $x {\geq} 2$} \end{cases}\) | 11. \(f(x)= \begin{cases} 5x & \text{if $x < 0$} \\ 3 & \text{if $0 {\geq} x {\leq} 2$} \\ x^2 & \text{if $x > 3$} \end{cases}\) |
Write the domain for each piecewise function in interval notation.
| 12. \(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\) | 13. \(f(x)= \begin{cases} x^2-2 & \text{if $x < 1$} \\ -x^2+2 & \text{if $x > 1$} \end{cases}\) | 14. \(f(x)= \begin{cases} x^2-3 & \text{if $x < 0$} \\ -3x^2 & \text{if $x {\geq} 2$} \end{cases}\) |
15. Find \(f(-5), f(0)\), and \(f(3)\) given \(f ( x ) = \left\{ \begin{array} { l l } { x ^ { 2 } } & { \text { if } x \leq 0 } \\ { x + 2 } & { \text { if } x > 0 } \end{array} \right. \\[5pt] \)
16. Find \(f(−3), f(0)\), and \(f(2)\) given \(f ( x ) = \left\{ \begin{array} { l l } { x ^ { 3 } } & { \text { if } x < 0 } \\ { 2 x - 1 } & { \text { if } x \geq 0 } \end{array} \right. \\[5pt] \)
17. Find \(g(−1), g(1)\), and \(g(4)\) given \(g ( x ) = \left\{ \begin{array} { l l } { 5 x - 2 } & { \text { if } x < 1 } \\ { \sqrt { x } } & { \text { if } x \geq 1 } \end{array} \right. \\[5pt] \)
18. Find \(g(−3), g(−2)\), and \(g(−1)\) given \(g ( x ) = \left\{ \begin{array} { l } { x ^ { 3 } \text { if } x \leq - 2 } \\ { | x | \text { if } x > - 2 } \end{array} \right.\)
19. Find \(h(−2), h(0)\), and \(h(4)\) given \(h ( x ) = \left\{ \begin{array} { l l } { - 5 } & { \text { if } x < 0 } \\ { 2 x - 3 } & { \text { if } 0 \leq x < 2 } \\ { x ^ { 2 } } & { \text { if } x \geq 2 } \end{array} \right. \\[5pt] \)
20. Find \(h(−5), h(4)\), and \(h(25)\) given \(h ( x ) = \left\{ \begin{array} { l } { - 3 x \text { if } x \leq 0 } \\ { x ^ { 3 } \text { if } 0 < x \leq 4 } \\ { \sqrt { x } \text { if } x > 4 } \end{array} \right.\)
21. Find \(f(−2), f(0)\), and \(f(3)\) given \(f ( x ) = {[{[x-0.5}]}] \\[5pt] \)
22. Find \(f(−1.2), f(0.4)\), and \(f(2.6)\) given \(f ( x ) = {[{[2x}]}]+ 1 \\[5pt] \)
- Answers to Odd Exercises:
-
7. \(f(−3)=1\); \(f(−2)=0\); \(f(−1)=0\); \(f(0)=0\)
9. \(f(−1)=−4\); \(f(0)=6\); \(f(2)=20\); \(f(4)=34\)
11. \(f(−1)=−5\); \(f(0)=3\); \(f(2)=3\); \(f(4)=16\)
13. domain: \((−\infty,1)\cup(1,\infty)\)
15. \(f (−5) = 25, f(0) = 0\), and \(f(3) = 5\)
17. \(g(−1) = −7, g(1) = 1\), and \(g(4) = 2\)
19. \(h(−2) = −5, h(0) = −3\), and \(h(4) = 16\)
21. \(f(−2) = −3, f(0) = −1\), and \(f(3) = 2\)
C: Graph Piecewise Functions
Exercise \(\PageIndex{C}\)
\( \bigstar \) Graph two-part piecewise functions.
|
|
|
- Answers to Odd Exercises:
-
23.
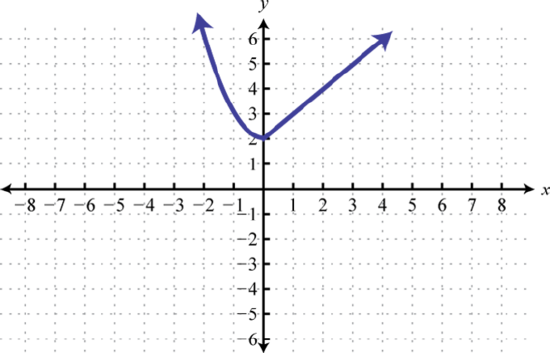
25.
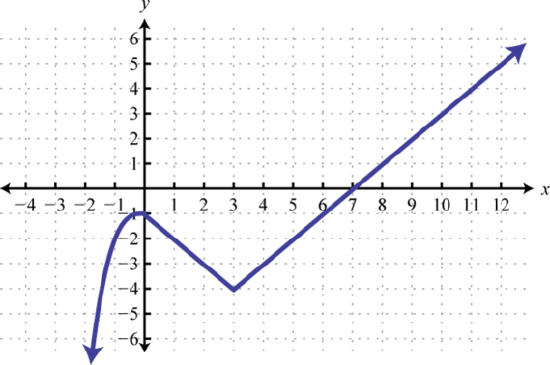
27.
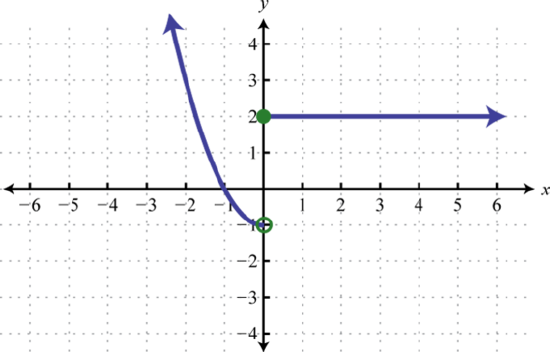 Figure 2.4.27
Figure 2.4.2729.
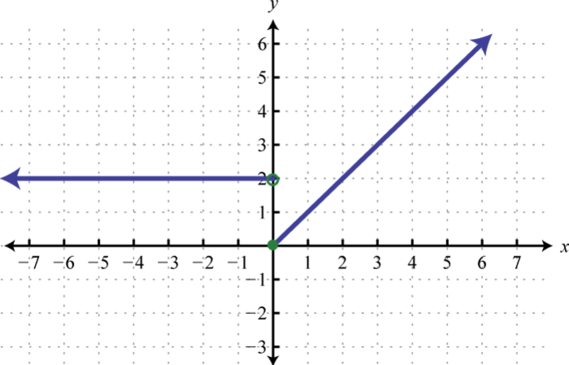
Figure 2.4.29 31.
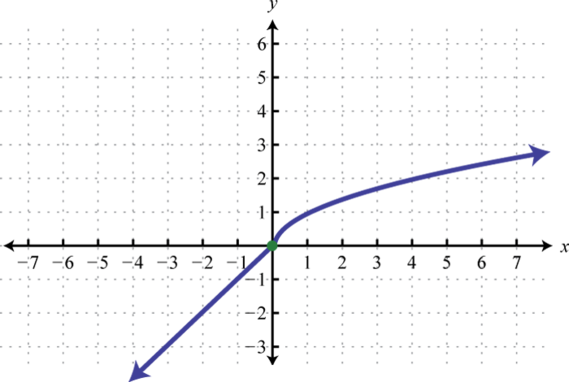
Figure 2.4.31 .
33.
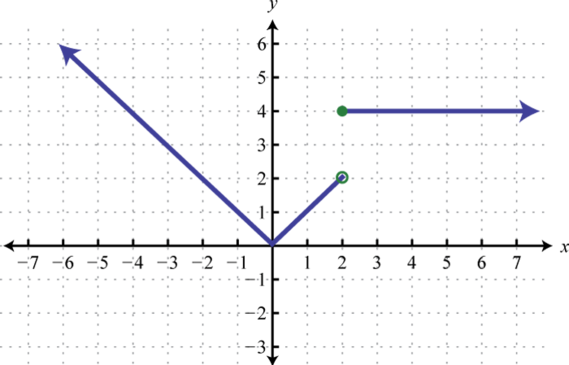
Figure 2.4.33 .
35.
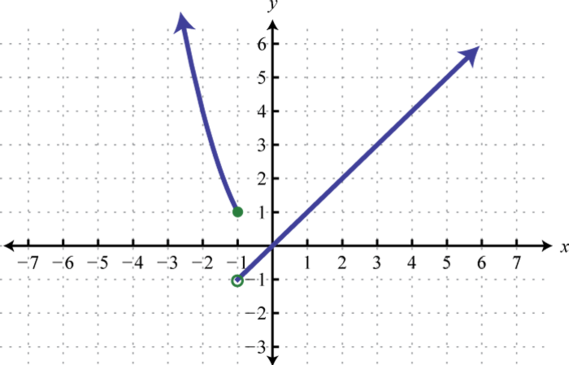
Figure 2.4.35 .
37.
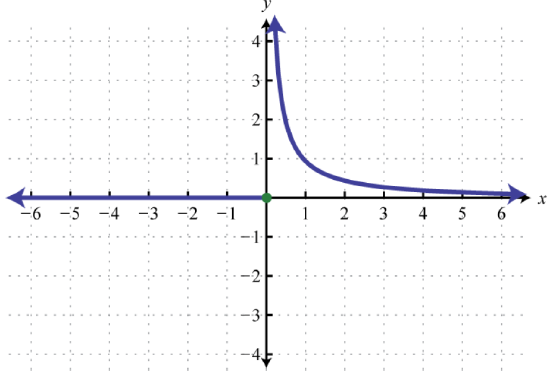
Figure 2.4.37 .
\( \bigstar \) Graph 3 or more part piecewise functions.
|
|
- Answers to Odd Exercises:
-
39. 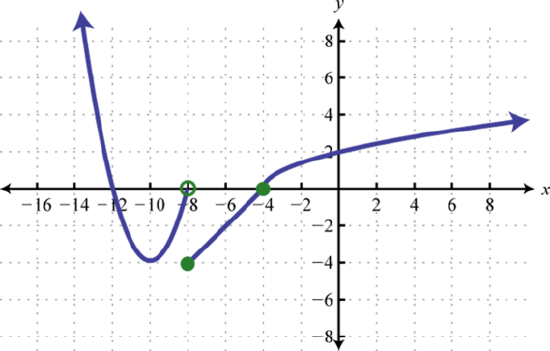
Figure 2.4.39
41.
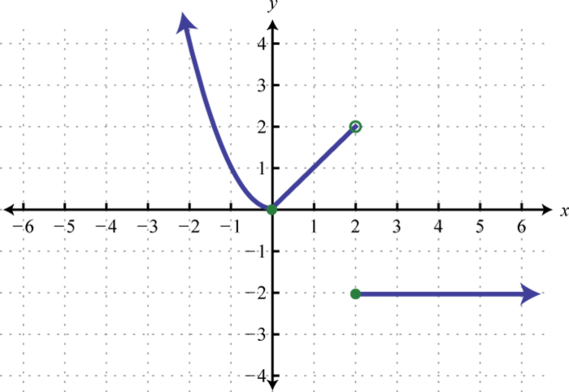
Figure 2.4.41 x
43. 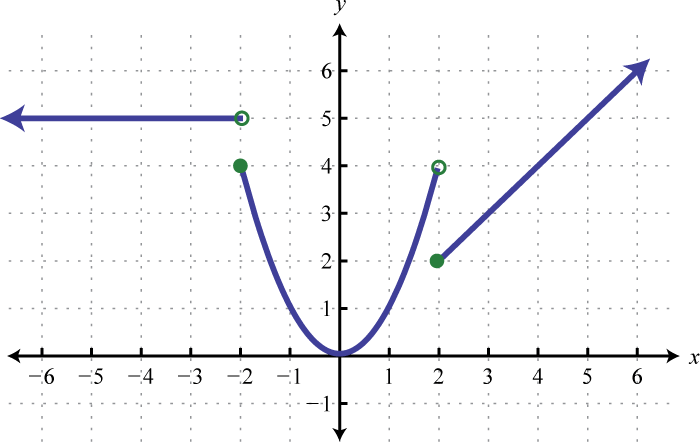
Figure 2.4.43 45.
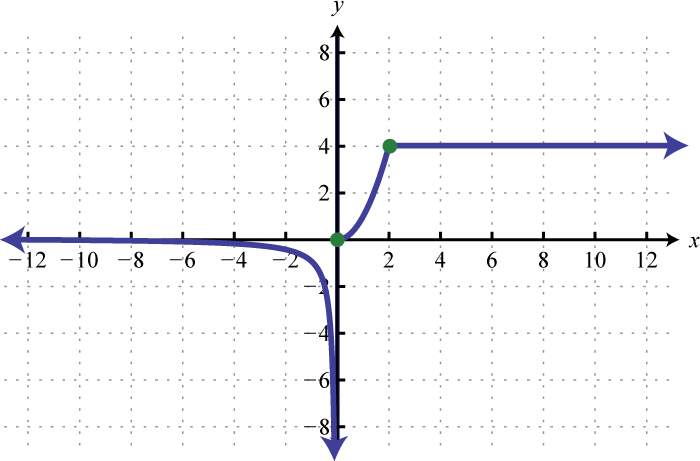
Figure 2.4.45 x
47. 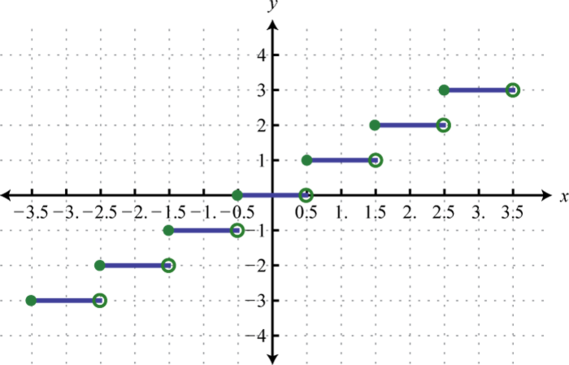
Figure 2.4.47 49.
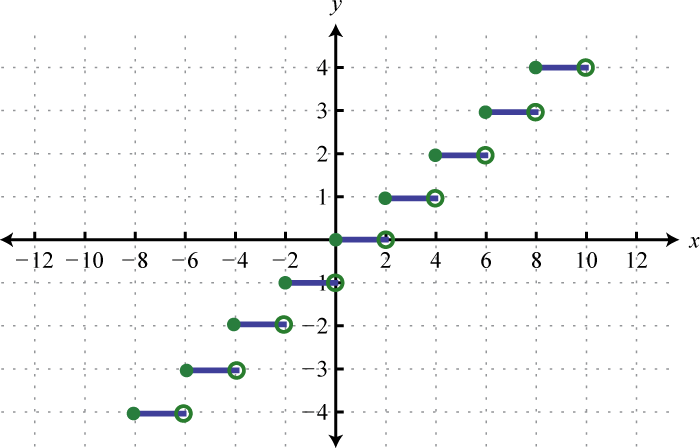
Figure 2.4.49 x
D: Graph Piecewise Functions and find their domain
Exercise \(\PageIndex{D}\)
\( \bigstar \) For each of the following, (a) graph the piecewise function, and (b) state its domain in interval notation.
|
51. \(f(x)= \begin{cases} 2x-1 & \text{if $x < 1$} \\ 1+x & \text{if $x {\geq} 1$} \end{cases}\) 52. \(f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}\) 53. \(f(x)= \begin{cases} 3 & \text{if $x < 0$} \\ \sqrt{x} & \text{if $x {\geq} 0$} \end{cases}\) |
54. \(f(x)= \begin{cases} x+1 & \text{if $x < 0$} \\ x-1 & \text{if $x > 0$} \end{cases}\) 55. \(f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ x+2 & \text{if $x {\geq} 0$} \end{cases}\) 56. \(f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ 1-x & \text{if $x > 0$} \end{cases}\) |
57. \(f(x)= \begin{cases} |x| & \text{if $x < 2$} \\ 1 & \text{if $x {\geq} 2$} \end{cases}\) 58. \(f(x)= \begin{cases} x+1 & \text{if $x < 1$} \\ x^3 & \text{if $x {\geq} 1$} \end{cases}\) |
- Answers to Odd Exercises:
-
51. domain: \((−\infty,\infty)\)
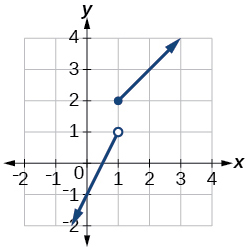
53. domain: \((−\infty,\infty)\)
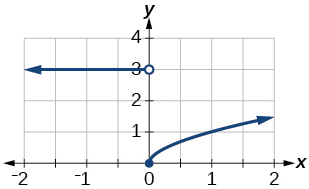
55. domain: \((−\infty,\infty)\)
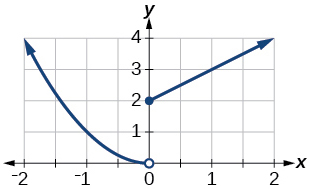
57. domain: \((−\infty,\infty)\)
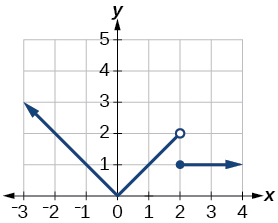
E: Graph Piecewise Functions and evaluate them
Exercise \(\PageIndex{E}\)
\( \bigstar \) For each of the piecewise-defined functions, (a) sketch the graph, and (b) evaluate at the given values of the independent variable.
|
59. \(f(x)=\begin{cases}x^2-3, & x≤0\\ 4x-3, & x>0\end{cases} \quad \text{Find } f(−4), \; f(0), \; f(2)\) 60. \(f(x)=\begin{cases}4x+3, & x≤0\\ -x+1, & x>0 \end{cases} \quad \text{Find } f(−3), \; f(0), \; f(2)\) |
61. \(g(x)=\begin{cases}\frac{3}{x−2}, &x≠2\\4, &x=2\end{cases} \quad \text{Find } g(0), \; g(−4), \; g(2)\) 62. \(h(x)=\begin{cases}x+1, &x≤5\\4, &x>5\end{cases} \quad \text{Find } h(0), \; h(π), \; h(5)\) |
- Answers to Odd Exercises:
-
59. \( f(−4)=13,\; f(0)=-3,\; f(2)=5\)
\(\qquad\)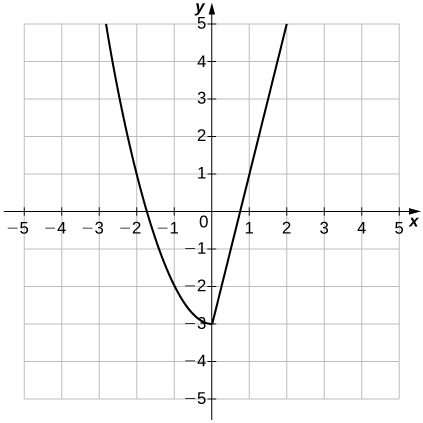
61. a. \(g(0)=\frac{−3}{2},\; g(−4)=\frac{−1}{2},\; g(2)=4 \)
\(\qquad\)
F: Construct the equation for a piecewise function given a graph
Exercise \(\PageIndex{F}\)
\( \bigstar \) (a) Evaluate piecewise function values from a graph. (b) Construct a piecewise function corresponding to the graph.
|
63. Find \(f(-4), f(-2)\), and \(f(0)\). 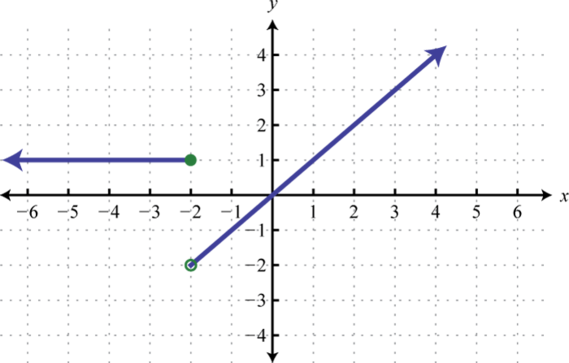
|
64. Find \(f(−3), f(0)\), and \(f(1)\). 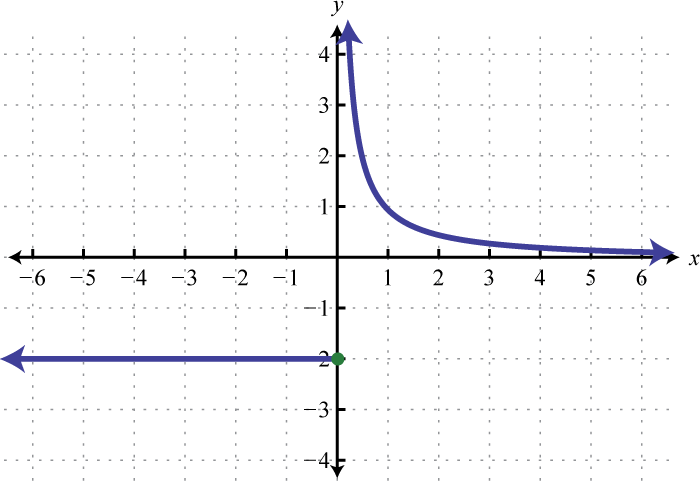
|
65. Find \(f(0), f(2)\), and \(f(4)\). 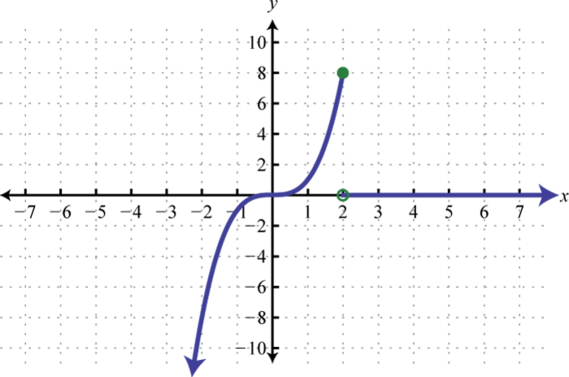
|
|
66. Find \(f(−5), f(−2)\), and \(f(2)\). 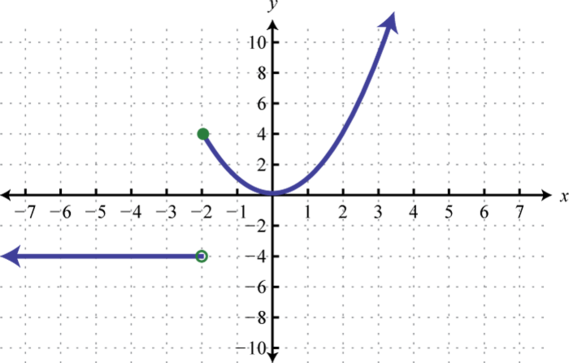
|
67. Find \(f(−3), f(−2)\), and \(f(2)\). 
|
68. Find \(f(−3), f(0)\), and \(f(4)\). 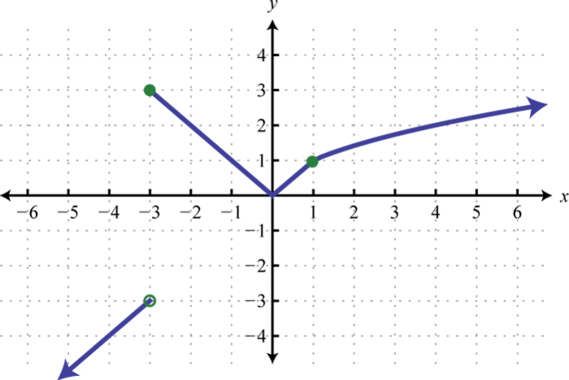
|
|
69. Find \(f(−2), f(0)\), and \(f(2)\). 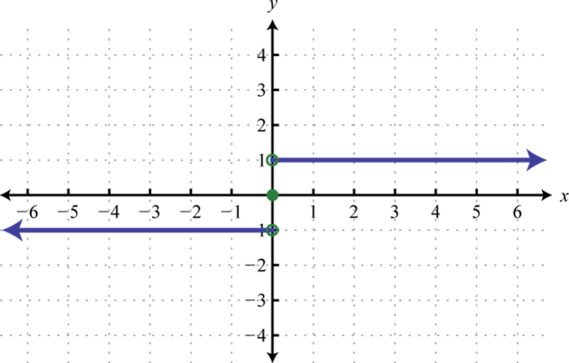
|
70. Find \(f(−3), f(1)\), and \(f(2)\). 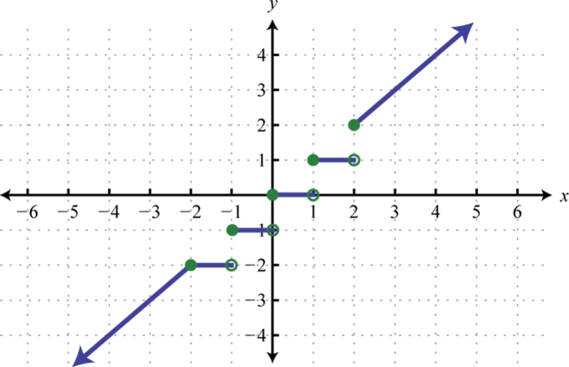
|
- Answers to Odd Exercises:
-
63. \(f(−4) = 1, f(−2) = 1\), and \(f(0) = 0 \qquad f(x)=\begin{cases}1, & x≤-2\\ x, & x>-2\end{cases} )\)
65. \(f(0) = 0, f(2) = 8\), and \(f(4) = 0 \qquad \qquad f(x)=\begin{cases}-2, & x≤0\\ \frac{1}{x}, & x>0\end{cases} \)
67. \(f(−3) = 5, f(−2) = 4\), and \(f(2) = 2 \qquad f(x)=\begin{cases}5, & x< -2\\x^2, & -2 \le x < 2\\ x, & x \ge 2\end{cases} \)
69. \(f(−2) = −1, f(0) = 0\), and \(f(2) = 1 \qquad f(x)=\begin{cases}-1, & x<0\\ 0, & x=0\\ 1, & x>0\end{cases} \)
G: Simplify Combination Functions and Find their Domains
Exercise \(\PageIndex{G}\)
\( \bigstar \) For each pair of functions \(f\) and \(g\) given below, find and simplify the combination functions \(f+g\), \(f−g\), \(fg\), and \(\dfrac{f}{g}\). State the domain of each combination functions in interval notation.
|
71. \(f(x)=x^2+2x,\) \(g(x)=6−x^2 \\[4pt] \). 72. \(f(x)=−3x^2+x,\) \(g(x)=5\). |
73. \(f(x)=2x^2+4x,\) \(g(x)=\dfrac{1}{2x}\). 74. \(f(x)=\dfrac{1}{x−4},\) \(g(x)=\dfrac{1}{6−x}\). |
75. \(f(x)=3x^2,\) \(g(x)=\sqrt{x−5}\). 76. \(f(x)=\sqrt{x},\) \(g(x)=|x−3|\) |
- Answers to Odd Exercises:
-
- \((f+g)(x)=2x+6\), domain: \((−\infty,\infty)\)
\((f−g)(x)=2x^2+2x−6\), domain: \((−\infty,\infty)\)
\((fg)(x)=−x^4−2x^3+6x^2+12x\), domain: \((−\infty,\infty)\)
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2+2x}{6−x^2},\) domain: \( (−\infty,−\sqrt{6})\cup(\sqrt{6},\sqrt{6})\cup(\sqrt{6},\infty)\)
- \((f+g)(x)=\dfrac{4x^3+8x^2+1}{2x}\), domain: \((−\infty,0)\cup(0,\infty)\)
\((f−g)(x)=\dfrac{4x^3+8x^2−1}{2x}\), domain: \((−\infty,0)\cup(0,\infty)\)
\((fg)(x)=x+2\), domain: \((−\infty,0)\cup(0,\infty)\)
\( \left(\dfrac{f}{g}\right) (x)=4x^3+8x^2\), domain: \((−\infty,0)\cup(0,\infty)\)
- \((f+g)(x)=3x^2+\sqrt{x−5}\), domain: \(\left[5,\infty\right)\)
\((f−g)(x)=3x^2−\sqrt{x−5}\), domain: \(\left[5,\infty\right)\)
\((fg)(x)=3x^2\sqrt{x−5}\), domain: \(\left[5,\infty\right)\)
\(\left(\dfrac{f}{g}\right)(x)=\dfrac{3x^2}{\sqrt{x−5}}\), domain: \((5,\infty)\)
- \((f+g)(x)=2x+6\), domain: \((−\infty,\infty)\)
Composition
H: Evaluate a Composition from Tables
Exercise \(\PageIndex{H}\)
\( \bigstar \) Use the function values for f and g shown in the table below to evaluate each expression.
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(f(x)\) | 7 | 6 | 5 | 8 | 4 | 0 | 2 | 1 | 9 | 3 |
| \(g(x)\) | 9 | 5 | 6 | 2 | 1 | 8 | 7 | 3 | 4 | 0 |
78. \(f(g(8))\) \(\;\) 79. \(f(g(5))\) \(\;\) 80. \(g(f(5))\) \(\;\) 81. \(g(f(3))\) \(\;\) 82. \(f(f(4))\) \(\;\) 83. \(f(f(1))\) \(\;\) 84. \(g(g(2))\) \(\;\) 85. \(g(g(6))\)
\( \bigstar \) Use the function values for f and g shown in the table below to evaluate each expression.
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| \(f(x)\) | 11 | 9 | 7 | 5 | 3 | 1 | -1 |
| \(g(x)\) | -8 | -3 | 0 | 1 | 0 | -3 | -8 |
86. \((f{\circ}g)(1)\) \(\quad\) 87. \((f{\circ}g)(2)\) \(\quad\) 88. \((g{\circ}f)(2)\) \(\quad\) 89. \((g{\circ}f)(3)\) \(\quad\) 90. \((g{\circ}g)(1)\) \(\quad\) 91. \((f{\circ}f)(3)\)
- Answers to Odd Exercises:
-
79. \(9\) 81. \(4\) 83. \(2\) 85. \(3\) 87. \(11\) 89. \(0\) 91. \( 7 \)
I: Evaluate a Composition from Graphs
Exercise \(\PageIndex{I}\)
\( \bigstar \) Use graphs to evaluate the following compositions.
|
92. \( (f \circ g ) (3) \\[5pt] \) 92.1 \( (f \circ g ) (6) \\[5pt] \) 93. \( (f \circ g ) (1) \\[5pt] \) 94. \( (g \circ f ) (1) \\[5pt] \) 95. \( (g \circ f ) (0) \) |
96. \( (f \circ f ) (5) \\[5pt] \) 97. \( (f \circ f ) (4) \\[5pt] \) 98. \( (g \circ g ) (2) \\[5pt] \) 99. \( (g \circ g ) (0) \) |
\(f\)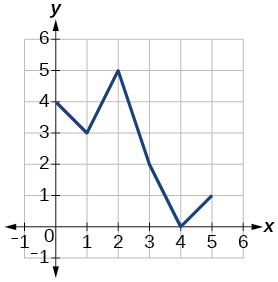 |
\(g\)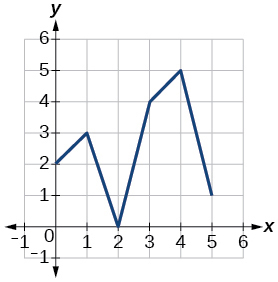 |
\( \bigstar \) Use graphs to evaluate the following compositions.
|
100. \(g(f(1)) \\[5pt] \) 101. \(g(f(2)) \\[5pt] \) 102. \(f(g(4)) \\[5pt] \) 103. \(f(g(1)) \\[5pt] \) 104. \(f(h(2)) \\[5pt] \) 105. \(h(f(2)) \\[5pt] \) 106. \(f(g(h(4))) \\[5pt] \) 107. \(f(g(f(−2)))\) |
|
- Answers to Odd Exercises:
-
93. \(2\) 95. \(5\) 97. \(4\) 99. \(0\) 101. \(2\) 103. \(1\) 105. \(4\) 107. \(4\)
J: Evaluate a Composition from Formulas
Exercise \(\PageIndex{J}\)
\( \bigstar \) Use the given pair of functions to find the following values if they exist.
| a. \((g\circ f)(0) \) | b. \((f\circ g)(-1) \) | c. \((f \circ f)(2) \) | d. \((g\circ f)(-3) \) | e. \((f\circ g)\left(\frac{1}{2}\right) \) | f. \((f \circ f)(-2) \) |
|
|
|
- Answers to Odd Exercises
-
111.\( f(x) = x^2 \), \( g(x) = 2x+1 \):
- \((g\circ f)(0) = 1 \)
- \((f\circ g)(-1) = 1 \)
- \((f \circ f)(2) = 16 \)
- \((g\circ f)(-3) = 19 \)
- \((f\circ g)\left(\frac{1}{2}\right) = 4 \)
- \((f \circ f)(-2) = 16 \)
113. \( f(x) = 4-3x \), \( g(x) = |x| \):
- \((g\circ f)(0) = 4 \)
- \((f\circ g)(-1) = 1 \)
- \((f \circ f)(2) = 10 \)
- \((g\circ f)(-3) = 13 \)
- \((f\circ g)\left(\frac{1}{2}\right) = \frac{5}{2} \)
- \((f \circ f)(-2) = -26 \)
115. \( f(x) = 4x+5 \), \( g(x) = \sqrt{x} \):
- \((g\circ f)(0) = \sqrt{5} \)
- \((f\circ g)(-1) \) is not real
- \((f \circ f)(2) = 57 \)
- \((g\circ f)(-3) \) is not real
- \((f\circ g)\left(\frac{1}{2}\right) = 5+2\sqrt{2} \)
- \((f \circ f)(-2) = -7 \)
117. \(f(x)=6-x-x^2 \),
\(\quad\)\( g(x)=x\sqrt{x+10}\)- \((g\circ f)(0) = 24 \)
- \((f\circ g)(-1) = 0 \)
- \((f \circ f)(2) = 6 \)
- \((g\circ f)(-3) = 0 \)
- \((f\circ g)\left(\frac{1}{2}\right) = \frac{27-2\sqrt{42}}{8} \)
- \((f \circ f)(-2) = -14 \)
119. \( f(x) = \frac{3}{1-x} \), \( g(x) = \frac{4x}{x^2+1} \):
- \((g\circ f)(0) = \frac{6}{5} \)
- \((f\circ g)(-1) = 1 \)
- \((f \circ f)(2) = \frac{3}{4} \)
- \((g\circ f)(-3) = \frac{48}{25} \)
- \((f\circ g)\left(\frac{1}{2}\right) = -5 \)
- \((f \circ f)(-2) \) is undefined
121. \( f(x) = \frac{2x}{5-x^2} \), \( g(x) = \sqrt{4x+1} \):
- \((g\circ f)(0) = 1 \)
- \((f\circ g)(-1) \) is not real
- \((f \circ f)(2) = -\frac{8}{11} \)
- \((g\circ f)(-3) = \sqrt{7} \)
- \((f\circ g)\left(\frac{1}{2}\right) = \sqrt{3} \)
- \((f \circ f)(-2) = \frac{8}{11} \)
K: Simplify a Composition and Find its Domain
Exercise \(\PageIndex{K}\): Find and simplify the Equation for a Composition
\( \bigstar \) Find and simplify (a) \( (f \circ g)(x)\), and (b) \( (g \circ f)(x)\). State the domain for (c) \( (f \circ g)(x)\) and for (d) \( (g \circ f)(x)\).
|
|
- Answers to Odd Exercises
-
127. a. \((f \circ g )(x) = (x+1)^5\), domain: \( (−\infty,\infty) \) \( \qquad \) b. \((g \circ f ) (x)= x^5+1 \). domain: \( (−\infty,\infty) \)
129. a. \((f \circ g )(x)= 2x^2-15 \), domain: \( (-\infty, \infty) \) \( \qquad \) b. \((g \circ f ) (x)= 4x^2+12x \), domain: \( (-\infty, \infty) \)
131. a. \((f \circ g )(x)= 27-10x^2\), domain: \( (−\infty,\infty) \) \( \; \) b. \((g \circ f ) (x)=-50x^2-140x-94 \). domain: \( (−\infty,\infty) \)
133. a. \((f \circ g )(x)= 2(3x−5)^2+1\), domain: \( (−\infty,\infty) \) \( \qquad \) b. \((g \circ f ) (x)= 6x^2−2\). domain: \( (−\infty,\infty) \)
135. a. \((f \circ g )(x)= x^2-4 \), domain: \( (-\infty, \infty) \) \( \qquad \) b. \((g \circ f ) (x)= |x^2-4| \), domain: \( (-\infty, \infty) \)
\( \bigstar \) Find and simplify (a) \( (f \circ g)(x)\), and (b) \( (g \circ f)(x)\). State the domain for (c) \( (f \circ g)(x)\) and for (d) \( (g \circ f)(x)\).
|
|
- Answers to Odd Exercises
-
137. a. \((f \circ g )(x)= 3 \sqrt{x} -5\), domain: \( [0, \infty) \) \( \qquad \) b. \((g \circ f ) (x)= \sqrt{3x-5} \). domain: \( [ \frac{5}{3}, \infty ) \)
139. a. \((f \circ g )(x)= \sqrt{x}+1 \), domain: \( [0,\infty) \)\( \qquad \) b. \((g \circ f ) (x)= \sqrt{|x+1|} \), domain: \( (-\infty, \infty) \)
141. a. \((f \circ g )(x)= x\), domain: \( [2, \infty) \)\( \qquad \) b. \((g \circ f ) (x)= |x| \). domain: \( (−\infty,\infty) \)
143. a. \((f \circ g )(x)= x-6- \sqrt{x-5}\), d: \( [5,\infty) \)\( \qquad \) b. \((g \circ f ) (x)= \sqrt{x^2-x-6} \). d: \( (−\infty,-2]\cup[3,\infty) \)
145. a. \((f \circ g )(x)= \frac{1}{\sqrt{x^2-4}}\), domain: \( (−\infty,−2)\cup(2,\infty) \)\( \qquad \) b. \((g \circ f ) (x)= \frac{1}{x}-4 \). domain: \( (0,\infty) \)
147. a. \((f \circ g )(x)= \sqrt{16-x^3}\), d: \( ( -\infty, 2\sqrt[3]{2} ] \)\( \qquad \) b. \((g \circ f ) (x)= 12-(x+4) \sqrt{x+4}\). d: \( [-4, \infty) \)
\( \bigstar \) Find and simplify (a) \( (f \circ g)(x)\), and (b) \( (g \circ f)(x)\). State the domain for (c) \( (f \circ g)(x)\) and for (d) \( (g \circ f)(x)\).
|
|
- Answers to Odd Exercises:
-
149. a. \((f \circ g )(x)= \frac{1}{x-3}\), domain: \( (−\infty,3)\cup(3,\infty) \)\( \qquad \) b. \((g \circ f ) (x)=\frac{1}{x}-3 \). domain: \( (−\infty,0)\cup(0,\infty) \)
151. a. \((f \circ g )(x)= -\frac{x}{x+3} \), d: \( \left(-\infty, -3\right) \cup \left(-3, \infty\right) \)\( \qquad \) b. \((g \circ f ) (x)= \frac{1}{3x+2} \), d: \( \left(-\infty, -\frac{2}{3}\right) \cup \left(-\frac{2}{3}, \infty\right) \)
153. a. \((f \circ g )(x)= \dfrac{x}{2} \), domain: \( (−\infty,0)\cup(0,\infty) \)\( \qquad \) b. \((g \circ f ) (x)=2x-4 \). domain: \( (−\infty,4)\cup(4,\infty) \)
155. a. \((f \circ g )(x)= \frac{2x+1}{5x+2} \), d: \( \left(-\infty, -\frac{2}{5}\right) \cup \left(-\frac{2}{5}, 0\right) \cup (0,\infty) \)
\( \qquad \;\) b. \((g \circ f ) (x)=\frac{4x+1}{x} \), domain: \( \left(-\infty, -\frac{1}{2}\right) \cup \left(-\frac{1}{2}, 0), \cup (0, \infty\right) \)
157. a. \((f \circ g )(x)= \frac{1}{\sqrt{x-1}}\), domain: \( (1,\infty) \)\( \qquad \) b. \((g \circ f ) (x)= \sqrt{\frac{1}{x}-1}\). domain: \( (0, 1] \)
159. a. \((f \circ g )(x)= \dfrac{\sqrt[3]{x+1}}{x} \), d: \( (−\infty,0)\cup(0,\infty) \)\( \qquad \) b. \((g \circ f ) (x)= \frac{\sqrt[3]{x}+1}{x} \). d: \( (−\infty,0)\cup(0,\infty) \)
\( \bigstar \) (a) Find and simplify \((f \circ f)(x) \)\ and (b) state the domain of the composition.
|
|
|
\( \bigstar \) Given \( f(x) = -2x \), \( g(x) = \sqrt{x} \) and \( h(x) = |x| \), find and simplify expressions for the following functions and state the domain of each using interval notation.
|
|
|
- Answers to Odd Exercises:
-
163. \((f \circ f)(x) = 4x+9 \), domain: \( (-\infty, \infty) \)
165. \((f \circ f)(x) =x^4-8x^2+12 \), domain: \( (-\infty, \infty) \)
167. \((f \circ f)(x) = ||x+1|+1| = |x+1|+1 \), domain: \( (-\infty, \infty) \)
169. \((f \circ f)(x) = | |x| | = |x| \), domain: \( (-\infty, \infty) \)
171. \((f \circ f)(x) = 9x-4 \), domain: \( (-\infty, \infty) \)
173. \((f \circ f)(x) = \frac{x}{4x+1} \), d: \( \left(-\infty, -\frac{1}{2}\right) \cup \left(-\frac{1}{2}, -\frac{1}{4} \right) \cup \left(-\frac{1}{4},\infty\right) \)
175. \((h\circ g \circ f)(x)= |\sqrt{-2x}|= \sqrt{-2x} \), domain: \( (-\infty, 0] \)
177. \((g\circ f \circ h)(x) = \sqrt{-2|x|} \), domain: \(\{0\} \)
179. \((f\circ h \circ g)(x) = -2|\sqrt{x}| = -2\sqrt{x} \), domain: \( [0,\infty) \)
L: Decomposition
Exercise \(\PageIndex{L}\)
\( \bigstar \) Find functions \(f(x)\) and \(g(x)\) so the given function can be expressed as \(f(g(x))\).
|
|
|
- Answers to Odd Exercises:
-
185. sample: \(f(x)=\sqrt{x}, \quad g(x)=\frac{2x−1}{3x+4}\)
187. sample: \(f(x)=x^3, \quad g(x)=x−5\)
189: sample: \(f(x)=\frac{4}{x}, \quad g(x)=(x+2)^2\)
191. sample: \(f(x)=\sqrt[3]{x}, \quad g(x)=\frac{1}{2x−3}\)
193. sample: \(f(x)=\sqrt[4]{x}, \quad g(x)=\frac{3x−2}{x+5}\)
195. sample: \(f(x)=\sqrt{x}, \quad g(x)=2x+6\)
197. sample: \(f(x)=\sqrt[3]{x}, \quad g(x)=(x−1)\)
199. sample: \(f(x)=x^3, \quad g(x)=\frac{1}{x−2}\)
201. Let \( g(x) = 2x+3 \) and \( f(x) = x^3 \), then \(p(x) = (f\circ g)(x) \).
203. Let \( g(x) = 2x-1 \) and \( f(x) = \sqrt{x} \), then \(h(x) = (f\circ g)(x) \).
205. Let \( g(x) = 5x+1 \) and \( f(x) = \frac{2}{x} \), then \(r(x) =(f\circ g)(x) \).
207. Let \( g(x) = |x| \) and \( f(x) = \frac{x+1}{x-1} \), then \(q(x) =(f\circ g)(x) \).
209. Let \( g(x) =2x \) and \( f(x) = \frac{x+1}{3-2x} \), then \(v(x) =(f\circ g)(x) \).