3.3: Power Functions and Polynomial Functions

Identifying Power Functions

A power function is a function with a single term that is the product of a real number (called a coefficient), and a variable raised to a fixed real number. For example, look at functions for the area of a circle or volume of a sphere with radius $r$.

$A(r)={\pi}r^2 \qquad \qquad V(r)=\dfrac{4}{3}{\pi}r^3$

Both of these are examples of power functions because they consist of a coefficient, ${\pi}$ or $\frac{4}{3}{\pi}$, multiplied by a variable $r$ raised to a fixed power.

Definition: Power Function

A power function is a function that can be represented in the form

\[f(x)=kx^p \label{power}\]

where parameters $k$ and $p$ are real numbers, $k$ is the coefficient and $p$ is the power of the function.

$QA.png$ Is $f(x)=2^x$ a power function?

No. The variable in a power function is in the base. This function has the variable in the exponent instead, so it is called an exponential function, not a power function.

Example $\PageIndex{1}$: Identify Equations of Power Functions

Which of the following functions are power functions?

$\begin{align*} f(x)&=1 &&\text{Constant function} \\f(x)&=x &&\text{Identity function} \\f(x)&=x^2 &&\text{Quadratic function} \\ f(x)&=x^3 &&\text{Cubic function} \\ \end{align*}$

\[\begin{align*} f(x)&=\dfrac{1}{x} &&\text{Reciprocal function} \\f(x)&=\dfrac{1}{x^2} &&\text{Reciprocal squared function} \\ f(x)&=\sqrt{x} &&\text{Square root function} \\ f(x)&=\sqrt[3]{x} &&\text{Cube root function} \end{align*}\]

Solution

All of the listed functions are power functions because they can be written in the form of Equation \ref{power}.

The constant and identity functions are power functions because they can be written as $f(x)=x^0$ and $f(x)=x^1$ respectively.
The quadratic and cubic functions are power functions with whole number powers $f(x)=x^2$ and $f(x)=x^3$.
The reciprocal and reciprocal squared functions are power functions with negative whole number powers because they can be written as $f(x)=x^{−1}$ and $f(x)=x^{−2}$.
The square and cube root functions are power functions with fractional powers because they can be written as $f(x)=x^{1/2}$ or $f(x)=x^{1/3}$.

$try-it.png$ Try It $\PageIndex{1}$

Which functions are power functions?

$f(x)=2x^2⋅4x^3$
$g(x)=−x^5+5x^3−4x$
$h(x)=\dfrac{2x^5−1}{3x^2+4}$

Answer: $f(x)$ is a power function because it can be written as $f(x)=8x^5$. The other functions are not power functions.

Identifying End Behavior of Power Functions

When describing power functions, what happens as numbers get very large is important. To describe the behavior as numbers become larger and larger, we use the idea of infinity. We use the symbol $\infty$ for positive infinity and $−\infty$ for negative infinity. When we say that “$x$ approaches infinity,” which can be symbolically written as $x{\rightarrow}\infty$, we are describing a behavior; we are saying that $x$ is increasing without bound. The behavior of the graph of a function as the magnitude of the input values gets very large $(x{\rightarrow}−{\infty}$ or $x{\rightarrow}{\infty})$ is referred to as the end behavior of the function. We can use words or symbols to describe end behavior.

Figure $\PageIndex{2}$ shows the graphs of $f(x)=x^2$, $g(x)=x^4$ and and $h(x)=x^6$, which are all power functions with even, whole-number powers. Notice that these graphs have similar shapes, very much like that of the quadratic function in the toolkit. However, as the power increases, the graphs flatten somewhat near the origin and become steeper away from the origin.

With these even-power functions, as the input increases or decreases without bound, the output values become very large, positive numbers. Equivalently, we could describe this behavior by saying that as $x$ approaches positive or negative infinity, the $f(x)$ values increase without bound. In symbolic form, we could write

$\text{as } x{\rightarrow}{\pm}{\infty}, f(x){\rightarrow}{\infty}$ or $ \displaystyle \lim_{x \to \pm \infty} (f(x) = \infty$

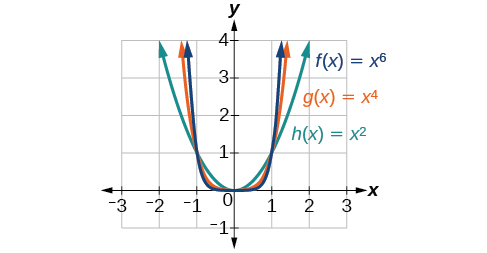$Graph of three functions, h(x)=x^2 in green, g(x)=x^4 in orange, and f(x)=x^6 in blue.$
Figure $\PageIndex{2}$: Even-power functions

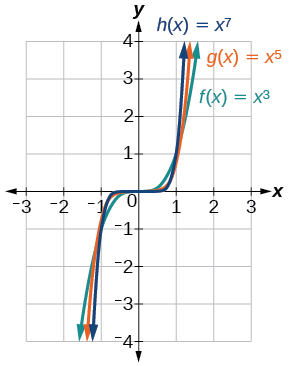
This example and the one below illustrate that functions of the form $f(x)=x^n$ reveal symmetry of one kind or another. First, in Figure $\PageIndex{2}$ above we see that even functions of the form $f(x)=x^n,$ $n$ even, are symmetric about the $y$-axis. In Figure $\PageIndex{3}$ below we see that odd functions of the form $f(x)=x^n,$ $n$ odd, are symmetric about the origin.

Figure $\PageIndex{3}$ shows the graphs of $f(x)=x^3$, $g(x)=x^5$, and $h(x)=x^7$, which are all power functions with odd, whole-number powers. Notice that these graphs look similar to the cubic function in the toolkit. Again, as the power increases, the graphs flatten near the origin and become steeper away from the origin.

For these odd power functions, as $x$ approaches negative infinity, $f(x)$ decreases without bound. As $x$ approaches positive infinity, $f(x)$ increases without bound. In symbolic form we write

$\begin{array}{ccc}
\text{as }x{\rightarrow}-{\infty},\;f(x){\rightarrow}-{\infty} &\text{ or } & \displaystyle \lim_{x \to -\infty} f(x) = -\infty \\
\text{as }x{\rightarrow}{\infty},\;f(x){\rightarrow}{\infty} &\text{ or } & \displaystyle \lim_{x \to \infty} f(x) = \infty \end{array}$

$Graph of three functions, f(x)=x^3 in green, g(x)=x^5 in orange, and h(x)=x^7 in blue.$

Figure $\PageIndex{3}$: Odd-power function

Figure $\PageIndex{4}$ below shows the end behavior of power functions in the form $f(x)=kx^n$ where $n$ is a non-negative integer depending on the power $n$ and the constant coefficient $k$.

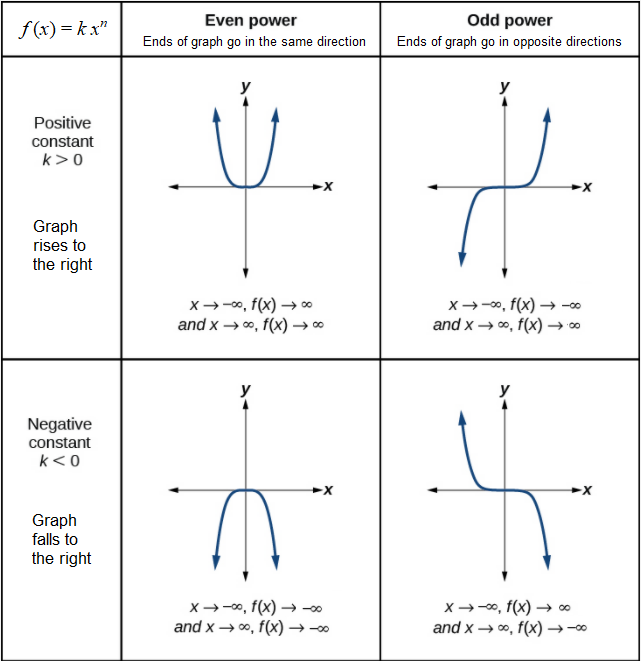
3.2 end behaviour graph.png — Figure $\PageIndex{4}$ End Behaviour of Power Functions

$how-to.png$ HowTo: Find the end behaviour of a power function $f(x)=kx^n$, $n$ is a non-negative integer.

Determine whether the constant coefficient $k$ is positive or negative.
- If positive, the graph rises on the right
- If negative, the graph falls on the right
Determine whether the power $n$ is even or odd.
- If even, the ends of the graph go in the same direction
- If odd, the ends of the graph go in opposite directions
The end behaviour analysis can be confirmed by looking at Figure $\PageIndex{4}$.

Example $\PageIndex{2}$: Identify End Behavior for an Equation of a Power Function

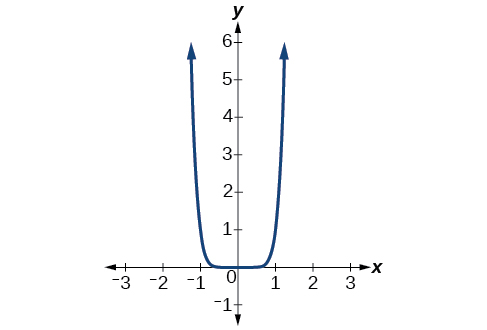
Describe the end behavior of the graph of $f(x)=x^8$.

Solution

Because the coefficient of the power function is 1 which is positive

The graph rises on the right.
More formally, as $x$ increases without bound, the output (value of $f(x)$ increases without bound.
Symbolically we write as $x→∞$, $f(x)→∞$.

Because the exponent of the power function is 8 (an even number)

Both ends of the graph go in the same direction (up)
As $x$ decreases without bound, $f(x)$ increases without bound.
As $x→−∞$, $f(x)→∞$.

The graph of the function is shown in Figure $\PageIndex{5}$.

Graph of f(x)=x^8 — Figure $\PageIndex{5}$: Graph of $f(x)=x^8$.

Example $\PageIndex{3}$:

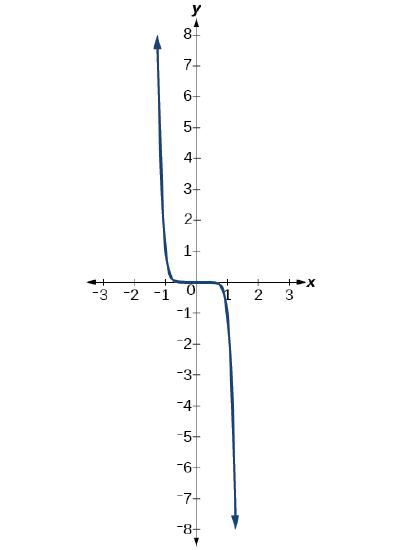
Describe the end behavior of the graph of $f(x)=−x^9$.

Solution

The exponent of the power function is 9 (an odd number).
The coefficient is –1 (negative).

Because the coefficient (-1) is negative

The graph falls on the right.
As $x$ increases without bound, $f(x)$ decreases without bound.
As $x→∞$, $f(x)→−∞$.

Because the exponent of the power function is 9 (an odd number)

The ends of the graph go in opposite directions (so the graph goes up on the left)
As $x$ decreases without bound, $f(x)$ increases without bound.
As $x→−∞$, $f(x)→∞$.

The graph of the function is shown in Figure $\PageIndex{6}$.

Graph of f(x)=-x^9 — Figure $\PageIndex{6}$: Graph of $f(x)=-x^9$.

$try-it.png$ Try It $\PageIndex{3}$

Describe in words and symbols the end behavior of $f(x)=−5x^4$.

Answer: Coefficient $-5$ is negative, so the graph falls on the right; as $x{\rightarrow}{\infty}$, $f(x){\rightarrow}−{\infty}$
Power $4$ is even, so the ends of the graph go in the same direction (down); as $x{\rightarrow}−{\infty}$, $f(x){\rightarrow}−{\infty}$

Identifying Polynomial Functions

A polynomial function consists of either zero or the sum of a finite number of non-zero terms, each of which is the product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.

Definition: Polynomial Functions

Let $n$ be a non-negative integer. A polynomial function is a function that can be written in the form

\[f(x)=a_nx^n+...+a_2x^2+a_1x+a_0 \label{poly}\]

This is called the general form of a polynomial function. Each $a_i$ is a coefficient and can be any real number. Each product $a_ix^i$ is a term of a polynomial function. Each exponent is a non-negative integer.

Example $\PageIndex{4}$: Identify Equations of Polynomial Functions

Which of the following are polynomial functions?

$f(x)=2x^3⋅3x+4$
$g(x)=−x(x^2−4)$
$h(x)=5\sqrt{x}+2$

Solution

The first two functions are examples of polynomial functions because they can be written in the form of Equation \ref{poly}, where the powers are non-negative integers and the coefficients are real numbers.

$f(x)$ can be written as $f(x)=6x^4+4$.
$g(x)$ can be written as $g(x)=−x^3+4x$.
$h(x)$ cannot be written in this form and is therefore not a polynomial function.

Identifying Polynomial Graphs

Polynomial functions have graphs that do not have sharp corners; these types of graphs are called smooth. Graphs of polynomial functions also have no breaks. Curves with no breaks are called continuous. The graphs of polynomial functions are both continuous and smooth.

Example $\PageIndex{5}$: Recognize Graphs of Polynomial Functions

Which of the graphs in Figure $\PageIndex{2}$ represents a polynomial function?

Solution

The graphs of $f$ and $h$ are graphs of polynomial functions. They are smooth and continuous.
The graphs of $g$ and $k$ are graphs of functions that are not polynomials. The graph of function $g$ has a sharp corner. The graph of function $k$ is not continuous.

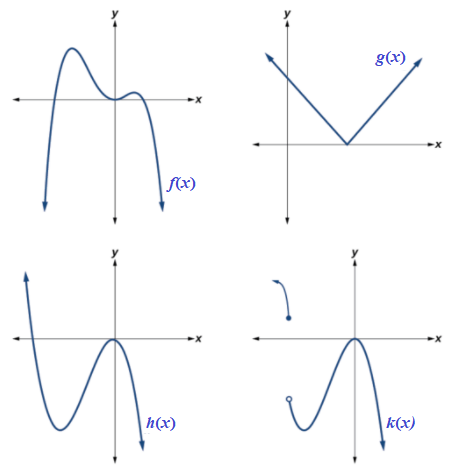$3.3 polynomials and not polynomials.png$
Figure $\PageIndex{2}$

$QA.png$ Do all polynomial functions have as their domain all real numbers?

Do all polynomial functions have as their domain all real numbers?

Yes. Any real number is a valid input for a polynomial function.

Identifying the Degree and Leading Coefficient of a Polynomial Function

Terminology of Polynomial Functions

degree is the highest power of the variable in the polynomial.
leading term is the term containing the highest power of the variable.
leading coefficient is the coefficient of the leading term.
general form is when terms are arranged in descending order of power.

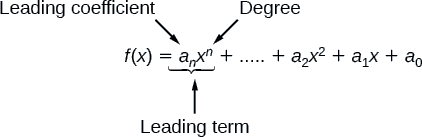$how-to.png$ How To: Given a polynomial function, identify the degree and leading coefficient

Find the highest power of $x$. This is the degree of the polynomial.
Identify the term containing the highest power of $x$. This is the leading term.
Identify the coefficient of the leading term. This is the leading coefficient.

Example $\PageIndex{6}$: Identify the Degree and Leading Coefficient of a Polynomial Function

Identify the degree, leading term, and leading coefficient of the following polynomial functions.

$f(x)=3+2x^2−4x^3$

$g(t)=5t^5−2t^3+7t$

$h(p)=6p−p^3−2$

Solution

For the function $f(x)$, the highest power of $x$ is 3, so the degree is 3. The leading term is the term containing that degree, $−4x^3$. The leading coefficient is the coefficient of that term, −4.
For the function $g(t)$, the highest power of $t$ is 5, so the degree is 5. The leading term is the term containing that degree, $5t^5$. The leading coefficient is the coefficient of that term, 5.
For the function $h(p)$, the highest power of $p$ is 3, so the degree is 3. The leading term is the term containing that degree, $−p^3$; the leading coefficient is the coefficient of that term, −1.

$try-it.png$ Try It $\PageIndex{7}$

Identify the degree, leading term, and leading coefficient of the polynomial $f(x)=4x^2−x^6+2x−5$.

Answer: The degree is 6. The leading term is $−x^6$. The leading coefficient is −1.

Identifying End Behavior of Polynomial Equations

Knowing the degree of a polynomial function is useful in helping us predict its end behavior. To determine its end behavior, look at the leading term of the polynomial function. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as $x$ grows without bound, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will match the end behavior of the term of highest degree. Therefore, the graphs of all polynomial functions will eventually rise or fall without bound when going far to the left or far to the right.

$how-to.png$ HowTo: Given a polynomial function, find its end behaviour

Identify the leading term of the polynomial
Examine the coefficient of the leading term to determine the end behaviour of the graph on the right.
- If positive, the graph rises on the right
- If negative, the graph falls on the right
Examine the degree of the leading term to determine how the ends of the graph behave relative to each other.
- If even, the ends of the graph go in the same direction
- If odd, the ends of the graph go in opposite directions

Graph		Ends go in the same direction	Ends go in opposite directions
	Leading Term	even power	odd power
Rises Right	positive coefficient	$ \nwarrow \dots \nearrow $	$ \swarrow \dots \nearrow $
Falls Right	negative coefficient	$ \swarrow \dots \searrow $	$ \nwarrow \dots \searrow $

Schematic Diagram of Polynomial End Behaviour

Because the end behaviour of a polynomial is determined by its leading term, which is a power function, the end behaviour of a polynomial is the same as that of a power function, as illustrated in Figure $\PageIndex{4}$.

Example $\PageIndex{8}$: Given an Equation of a Polynomial Function, State its End Behavior

Given the following polynomial functions, determine its leading term, degree, and end behavior.

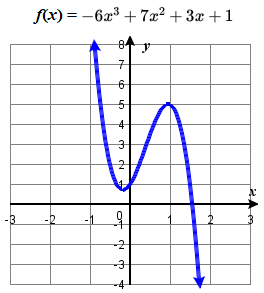
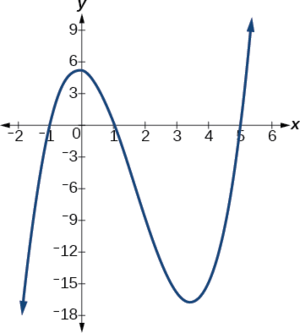
(a) $ 5x^4+2x^3−x−4$ $ \quad $ (b) $ 3x^5−4x^4+2x^2+1 $ $ \quad $ (c) $ −2x^6−x^5+3x^4+x^3 $$ \quad $ (d) $ −6x^3+7x^2+3x+1 $

Solution

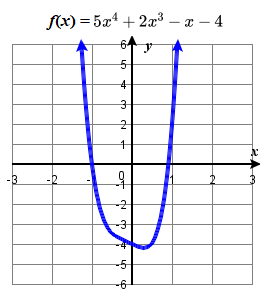
(a) Polynomial Function: $ 5x^4+2x^3−x−4$

Leading Term: $ 5x^4$ (degree 4)

positive so graph rises to the right and
even degree so ends go in the same direction: $ \nwarrow \ldots \nearrow $

Graph:

$3.3 example 8a.png$

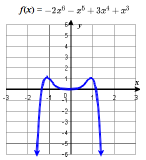
(c) Polynomial Function: $ −2x^6−x^5+3x^4+x^3 $

Leading Term: $ −2x^6 $ (degree 6)

negative so graph falls to the right and
even degree so ends go in the same direction: $ \swarrow \dots \searrow $

Graph:

$3.3 example 8c.png$

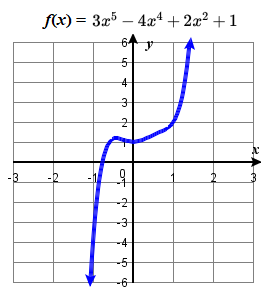
(b) Polynomial Function: $ 3x^5−4x^4+2x^2+1 $

Leading Term: $ 3x^5$ (degree 5)

positive so graph rises to the right and
odd degree so ends go in opposite directions: $ \swarrow \ldots \nearrow $

Graph:

$3.3 example 8b.png$

(d) Polynomial Function: $ −6x^3+7x^2+3x+1 $

Leading Term: $ −6x^3 $ (degree 3)

negative so graph falls to the right and
odd degree so ends go in opposite directions: $ \nwarrow \ldots \searrow $

Graph:

$3.3 example 8d.png$

$how-to.png$ How to: Given a factored polynomial, determine its leading term

Multiply the high order terms of each of the factors.
The result is the leading term of the polynomial.

Example $\PageIndex{9}$

Given the function $f(x)=−3x^2(x−1)(x+4)$, determine its leading term, degree, and end behavior.

Solution

One could begin by expanding $f(x)$ to obtain the general form of the polynomial, $ f(x)=−3x^2(x−1)(x+4) $. HOWEVER, this involves a lot of unnecessary work because the only term of interest is the leading term. The leading term of $ f(x)=−3x^2(x−1)(x+4) = {\color{Cerulean}{−3x^2}} ( {\color{Cerulean}{x}} -1)( {\color{Cerulean}{x}} +4) $ is the product of the $ {\color{Cerulean}{\textrm{leading terms}}}$ in each of the factors. So in this example, the leading term is simply the product $ {\color{Cerulean}{−3x^2}}({\color{Cerulean}{x}})({\color{Cerulean}{x}})=−3x^4 $. Thus the leading coefficient is negative (–3), so the graph falls to the right $ \ldots\searrow $ and the degree of the polynomial is 4, which is an even number, so the ends of the graph go in the same direction ( $ \swarrow\ldots\searrow $ ), or more formally, $\text{as }x{\rightarrow}−{\infty}, f(x){\rightarrow}−{\infty}$ and $\text{as } x{\rightarrow}{\infty}, f(x){\rightarrow}−{\infty}$

$try-it.png$ Try It $\PageIndex{10}$

Given the function $f(x)=0.2(x−2)(4x+1)^3(x−5)^3$, determine its leading term, degree, and end behavior.

Answer: The leading term is $0.2(x)(4x)^3(x)^3 = 12.8x^7$, so it is a degree 7 polynomial. As $x$ approaches positive infinity, $f(x)$ increases without bound; as $x$ approaches negative infinity, $f(x)$ decreases without bound. (rises to the right, ends in opposite directions: $ \swarrow\ldots\nearrow $ )

Intercepts of Polynomials

$how-to.png$ How to: Given a polynomial function, determine its intercepts

Determine the $y$-intercept by setting $x=0$ and finding $y$.
If the polynomial function is factorable, factor it into a product of linear and irreducible quadratic factors.
Set each factor equal to zero and solve. The $x$-intercepts are the solutions (or zeros) that are real numbers.
A polynomial of degree $n$ has $n$ zeros. Some of these zeros can have the same value; some can be imaginary.

Example $\PageIndex{11}$: Find Intercepts of a Factored Polynomial

Given the polynomial function $f(x)=(x−2)(x+1)(x−4)$, determine the $y$-and $x$-intercepts, the leading term, and the end behaviour.

Solution

The $y$-intercept occurs when the input is zero, so substitute 0 for $x$.

$f(0)=(0−2)(0+1)(0−4) =(−2)(1)(−4) =8 $

The $y$-intercept is $(0,8)$.

The $x$-intercepts occur when the output is zero.

\[ 0=(x−2)(x+1)(x−4) \nonumber \]

\[\begin{align*} x−2&=0 & &\text{or} & x+1&=0 & &\text{or} & x−4&=0 \\ x&=2 & &\text{or} & x&=−1 & &\text{or} & x&=4 \end{align*}\]

The $x$-intercepts are $(2,0)$,$(–1,0)$, and $(4,0)$.

The leading term is $(x)(x)(x) = x^3$. Therefore the graph rises to the right (positive coefficient) and falls to the left (odd degree so ends go in opposite directions): $ \swarrow \dots \nearrow $

Example $\PageIndex{12}$

Find the $y$- and $x$-intercepts of $g(x)=(x−2)^2(2x+3)$. Find the leading term and describe the end behaviour.

Solution

The $y$-intercept can be found by evaluating $g(0)$.

\[\begin{align*} g(0)&=(0−2)^2(2(0)+3) =12 \end{align*}\]

So the $y$-intercept is $(0,12)$.

The $x$-intercepts can be found by solving $g(x)=0$.

\[(x−2)^2(2x+3)=0 \nonumber \]

\[\begin{align*} (x−2)^2&=0 & & & (2x+3)&=0 \\ x−2&=0 & &\text{or} & x&=−\dfrac{3}{2} \\ x&=2 \end{align*}\]

So the $x$-intercepts are $(2,0)$ and $\left(−\dfrac{3}{2},0\right)$.

The leading term is $(x)^2(2x)=2x^3$. Therefore the graph rises to the right (positive coefficient) and falls to the left (odd degree so ends go in opposite directions): $ \swarrow \dots \nearrow $

Example $\PageIndex{13}$: Find $x$-intercepts of a Polynomial Function by Factoring

Find the $y$- and $x$-intercepts for $f(x)=x^3−5x^2−x+5$.

Solution

The $y$-intercept is $(0,5) $ because $f(0)=5$.

Find solutions for $f(x)=0$ by factoring.

\[\begin{align*} x^3−5x^2−x+5&=0 &&\text{Factor by grouping.} \\ x^2(x−5)−(x−5)&=0 &&\text{Factor out the common factor.} \\ (x^2−1)(x−5)&=0 &&\text{Factor the difference of squares.} \\ (x+1)(x−1)(x−5)&=0 &&\text{Set each factor equal to zero.} \end{align*}\]

\[\begin{align*} x+1&=0 & &\text{or} & x−1&=0 & &\text{or} & x−5&=0 \\ x&=−1 &&& x&=1 &&& x&=5\end{align*}\]

There are three $x$-intercepts: $(−1,0)$, $(1,0)$, and $(5,0)$.

$Graph of f(x)=x^3-5x^2-x+5 with its three intercepts (-1, 0), (1, 0), and (5, 0).$

Figure $\PageIndex{13}$: Graph of $f(x)$.

$try-it.png$ Try It $\PageIndex{14}$

Given the polynomial function $f(x)=2x^3−6x^2−20x$, determine the $y$- and $x$-intercepts. Find the leading term and describe the end behaviour.

Answer: $y$-intercept $(0,0)$; $x$-intercepts $(0,0)$,$(–2,0)$, and $(5,0)$. The leading term is $2x^3$. The curve rises to the right (positive coefficient) and falls to the left (odd degree so ends go in opposite directions): $ \swarrow \dots \nearrow $

$try-it.png$ Try It $\PageIndex{15}$

Find the $y$- and $x$-intercepts of the function $f(x)=x^4+5x^3−4x^2−20x$. Find the leading term and describe the end behaviour.

Answer

$y$-intercept $(0,0)$;
$x$-intercepts $(0,0)$, $(–2,0)$, $(2,0)$, and $(-5,0)$.
The leading term is $x^4,$ so the curve rises both on the left and on the right: $ \nwarrow \dots \nearrow $

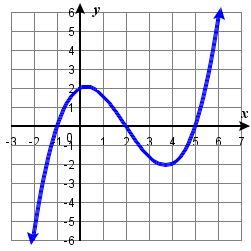
Example $\PageIndex{16}$: Given a graph of a polynomial, find a possible degree for it

Describe the end behavior and characteristics of the leading term and degree of the polynomial function in the figure below

$3.3 example 16.png$

Figure $\PageIndex{16}$.

Solution

The graph rises to the right $\dots \nearrow$ so the leading coefficient must be positive.

As the input values $x$ get very large, the output values $f(x)$ increase without bound.
$\text{As } x{\rightarrow}{\infty}, f(x){\rightarrow}{\infty}$

The ends go in opposite directions (the graph falls to the left) so the degree of the polynomial must be odd.

As the input values $x$ get very small, the output values $f(x)$ decrease without bound.
$\text{as } x{\rightarrow}−{\infty}, f(x){\rightarrow}−{\infty}$

3. Because there are 3 $x$-intercepts, the degree is at least three.

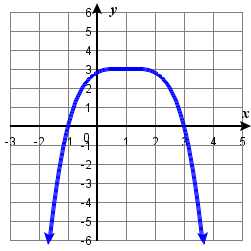
$try-it.png$ Try It $\PageIndex{17}$

Describe the end behavior, and characteristics of the leading term and degree of the polynomial function in the Figure below.

$3.3 try it 16.png$
Figure TryIt $\PageIndex{17}$

Answer

The graph falls to the right $\dots \searrow$ so the leading coefficient must be negative.
- As $x{\rightarrow}{\infty}$, $f(x){\rightarrow}−{\infty}$;
The ends go in the same direction (down) so the degree of the polynomial must be even.
- As $x{\rightarrow}−{\infty}$, $f(x){\rightarrow}−{\infty}$
Because there are 2 $x$-intercepts, the degree must be at least 2.

Key Equations

general form of a polynomial function: $f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0$

Key Concepts

A power function is a variable base raised to a number power.
The behavior of a graph as the input decreases beyond bound and increases beyond bound is called the end behavior.
The end behavior depends on whether the power is even or odd and the sign of the leading term.
A polynomial function is the sum of terms, each of which consists of a transformed power function with positive whole number power.
The degree of a polynomial function is the highest power of the variable that occurs in a polynomial. The term containing the highest power of the variable is called the leading term. The coefficient of the leading term is called the leading coefficient.
The end behavior of a polynomial function is the same as the end behavior of the power function that corresponds to the leading term of the function.

Glossary

coefficient $ \qquad $ a nonzero real number multiplied by a variable raised to an exponent
continuous function $ \qquad $ a function whose graph can be drawn without lifting the pen from the paper because there are no breaks in the graph
degree $ \qquad $ the highest power of the variable that occurs in a polynomial
end behavior $ \qquad $ the behavior of the graph of a function as the input decreases without bound and increases without bound
leading coefficient $ \qquad $ the coefficient of the leading term
leading term $ \qquad $ the term containing the highest power of the variable
polynomial function $ \qquad $ a function that consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.
power function $ \qquad $ a function that can be represented in the form $f(x)=kx^p$ where $k$ is a constant, the base is a variable, and the exponent, $p$, is a constant
smooth curve $ \qquad $ a graph with no sharp corners
term of a polynomial function $ \qquad $ any $a_ix^i$ of a polynomial function in the form $f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0$