4.1e: Exercises - Exponential Functions

A: Concepts

Exercise \(\PageIndex{A}\) 

1. Explain why the values of an increasing exponential function will eventually overtake the values of an increasing linear function.

2. Given a formula for an exponential function, is it possible to determine whether the function grows or decays exponentially just by looking at the formula? Explain.

3. The Oxford Dictionary defines the word nominal as a value that is “stated or expressed but not necessarily corresponding exactly to the real value.” Develop a reasonable argument for why the term nominal rate is used to describe the annual percentage rate of an investment account that compounds interest.

4. Why is \(b = 1\) excluded as a base in the definition of exponential functions? Explain.

5. Explain why an exponential function of the form \(y = b^{x}\) can never be negative.

Answers to odd exercises:

1. Linear functions have a constant rate of change. Exponential functions increase based on a percent of the original.

3. When interest is compounded, the percentage of interest earned to principal ends up being greater than the annual percentage rate for the investment account. Thus, the annual percentage rate does not necessarily correspond to the real interest earned, which is the very definition of nominal.

5. Since the base b must always be positive, raising a positive number to any power will always be positive

B: Identify Exponential Functions

Exercise \(\PageIndex{B}\) 

\( \bigstar \) For the following exercises, identify whether the statement represents an exponential function. Explain.

6) The average annual population increase of a pack of wolves is \(25\).

7) A population of bacteria decreases by a factor of \(\frac{1}{8}\) every \(24\) hours.

8) The value of a coin collection has increased by \(3.25\%\:\) annually over the last \(20\) years.

9) For each training session, a personal trainer charges his clients \(\$5\) less than the previous training session.

10) The height of a projectile at time \(t\) is represented by the function \(h(t)= -4.9t^2 + 18t + 40\)

\( \bigstar \) For the following exercises, determine whether the table could represent a function that is linear, exponential, or neither. If it appears to be exponential, find a function that passes through the points.

11(a) \(x\) 1 2 3 4 \(f(x)\) 70 40 10 -20

11(b) \(x\) 1 2 3 4 \(m(x)\) 80 61 42.9 25.61

11(c) \(x\) 1 2 3 4 \(g(x)\) 3 6 12 24

12(a) \(x\) 1 2 3 4 \(h(x)\) 70 49 34.3 24.01

12(b) \(x\) 1 2 3 4 \(f(x)\) 10 20 40 80

12(c) \(x\) 1 2 3 4 \(g(x)\) -3.25 2 7.25 12.5

14. Determine whether the following are exponential functions or not

(a) \(.381^{x-1}\)

(b) \((-2.7)^x\)

(c) \(\dfrac{2}{5^x}\)

(d) \(x^4+3x^2\)

(e) \(\dfrac{3}{6-x}\)

(f) \(x^2\)

(g) \(1^x\)

(h) \(3^x\)

Answers to odd exercises:

7. exponential; the population decreases by a proportional rate.

9. not exponential; the charge decreases by a constant amount each visit, so the statement represents a linear function.

11. (a) Linear, \(\quad\) (b) Neither, \(\quad\) (c) Exponential

C: Evaluate Exponential Functions

Exercise \(\PageIndex{C}\) 

\( \bigstar \) For the following exercises, evaluate each function. Give an exact answer.

17. \(f(x)=3^{x}\) for \(f(-2), f(0),\) and \(f(2)\). 18. \(f(x)=10^{x}\) for \(f(-1), f(0),\) and \(f(1)\). 19. \(g(x)=\left( 1 - \frac{2}{3} \right)^{x}\) for \(g(-1), g(0),\) and \(g(3)\). 20. \(g(x)=\left( 1 - \frac{1}{4} \right)^{x}\) for \(g(-2), g(-1),\) and \(g(0)\). 21. \(h(x)=(1+8)^{-x}\) for \(h(-1), h(0),\) and \(h\left(\frac{1}{2}\right)\).

22. \(h(x)=(1+3)^{-x}\) for \(h(-1), h\left(-\frac{1}{2}\right),\) and \(h(0)\). 23. \(f(x)=-2^{x}+1\) for \(f(-1), f(0),\) and \(f(3)\). 24. \(f(x)=2-3^{x}\) for \(f(-1), f(0),\) and \(f(2)\). 25. \(g(x)=10^{-x}+20\) for \(g(-2), g(-1),\) and \(g(0)\). 26. \(g(x)=1-2^{-x}\) for \(g(-1), g(0),\) and \(g(1)\).

Answers to odd exercises:

17. \(f(-2)=\frac{1}{9}, f(0)=1, f(2)=9\) 19. \(g(-1)=3, g(0)=1, g(3)=\frac{1}{27}\)

21. \(h(-1)=9, h(0)=1, h\left(\frac{1}{2}\right)=\frac{1}{3}\) 23. \(f(-1)=\frac{1}{2}, f(0)=0, f(3)=-7\)

25. \(g(-2)=120, g(-1)=30, g(0)=21\)

\( \bigstar \) For the following exercises, evaluate each function. Round answers to two decimal places, if necessary.

27) \(f(x)=-4^{2x+3}\) for \(f(-1)\) 28) \(f(x)=2(5)^x\) for \(f(-3)\) 29) \(f(x)=-2e^{x-1}\), for \(f(-1)\) 30) \(f(x)=e^x\), for \(f(3)\) 31) \(f(x)=1.2e^{2x}-0.3\), for \(f(3)\) 32) \(f(x)=2.7(4)^{-x+1}+1.5\), for \(f(-2)\) 33) \(g(x)=\frac{1}{3}(7)^{x-2}\) for \(g(6)\). 34) \(f(x)=-\frac{3}{2}(3)^{-x}+\frac{3}{2}\), for \(f(2)\) 35) \(h(x)=-\frac{1}{2}\left ( \frac{1}{2} \right )^x+6\) for \(h(-7)\). 36) \(f(x)=4(2)^{x-1}-2\) for \(f(5)\). 37) \(f(x)=5^x\) a. \(x=3\) b. \(x=\frac{1}{2}\) c. \(x=\sqrt{2}\) 38) \(f(x)=(1 - 0.7)^x\) a. \(x=−1\) b. \(x=4\) c. \(x=−1.5\)

39) \(f(x)=10^x\) a. \(x=−2\) b. \(x=4\) c. \(x=\frac{5}{3}\) 40) \(f(x)=e^x\) a. \(x=2\) b. \(x=−3.2\) c. \(x=π\) 41. \(f(x)=2^{x}+5\) for \(f(2.5)\). 42. \(f(x)=3^{x}-10\) for \(f(3.2)\). 43. \(g(x)=4^{x}\) for \(g(\sqrt{2})\). 44. \(g(x)=5^{x}-1\) for \(g(\sqrt{3})\). 45. \(h(x)=10^{x}\) for \(h(\pi)\). 46. \(h(x)=10^{x} + 1\) for \(h\left(\frac{\pi}{3}\right)\). 47. \(f(x)=10^{-x}-2\) for \(f(1.5)\). 48. \(f(x)=5^{-x}+3\) for \(f(1.3)\). 49. \(f(x)=\left(1 - \frac{1}{3}\right)^{x}+1\) for \(f(-2.7)\). 50. \(f(x)=\left( 1 - \frac{2}{5}\right)^{-x}-1\) for \(f(1.4)\).

Answers to odd exercises:

27. \(f(-1)=-4\) 29. \(f(-1)\approx -0.27\) 31. \(f(3)\approx 483.81\)

33. \(g(6)=800+\frac{1}{3}\approx 800.33\) 35. \(h(-7)=-58\) 37: \(a. 125 \quad b. 2.24 \quad c. 9.74\)

39: \(a. 0.01 \quad b. 10,000 \quad c. 46.42\) 41. \(10.66\) 43. \(7.10\)

45. \(1385.46\) 47. \(−1.97\) 49. \(3.99\)

\( \bigstar \) Find \(f (−1), f (0)\), and \(f (\frac{3}{2})\) for the given function. Use a calculator where appropriate to approximate to the nearest hundredth.

51. \(f(x)=e^{x}+2\) 52. \(f(x)=e^{x}-4\)

53. \(f(x)=5-3 e^{x}\) 54. \(f(x)=e^{-x}+3\)

55. \(f(x)=1+e^{-x}\) 56. \(f(x)=3-2 e^{-x}\)

57. \(f(x)=e^{-2 x}+2\) 58. \(f(x)=e^{-x^{2}}-1\)

Answers to odd exercises:

51. \(f(-1) \approx 2.37, f(0)=3, f\left(\frac{3}{2}\right) \approx 6.48\) 53. \(f(-1) \approx 3.90, f(0)=2, f\left(\frac{3}{2}\right) \approx-8.45\)

55. \(f(-1) \approx 3.72, f(0)=2, f\left(\frac{3}{2}\right) \approx 1.22\) 57. \(f(-1) \approx 9.39, f(0)=3, f\left(\frac{3}{2}\right) \approx 2.05\)

D: Exponential Growth - Identify Initial Value, Growth Factor and Growth Rate

Exercise \(\PageIndex{D}\) 

\( \bigstar \) For the following exercises, determine whether the equation represents exponential growth, exponential decay, or neither. Explain. State the growth factor and growth rate.

59) \(y=220(1.06)^x\)

60) \(y=300(1−t)^5\)

61) \(y=11,701(0.97)^t\)

62) \( y = 16.5 (1.025)^{\frac{1}{x}}\)

\( \bigstar \) For the following exercises, determine whether the equation represents continuous growth, continuous decay, or neither. Explain. State the growth rate and the growth factor.

63) \(y=3742(e)^{0.75t}\)

64) \(y=150(e)^{\frac{3.25}{t}}\)

65) \(y=2.25(e)^{-2t}\)

Answers to odd exercises:

59. exponential growth; The growth factor, \(1.06\) is greater than \(1\). The growth rate of \(6\%\) is positive.

61. exponential decay; The decay factor,  \(0.97\) is between \(0\) and \(1\). The growth rate of \(-3\%\) is negative.

63. continuous growth; the growth rate \(.75\), is greater than \(0\). The growth factor is \(e^{.75}\)

65. continuous decay; the growth rate \(-2\), is less than  \(0\). The decay factor is \(e^{-2}\).

\( \bigstar \) For the following exercises, consider this scenario. For each year \(t\), the population of a forest of trees is represented by the function\(A(t)=115(1.025)^t\). In a neighboring forest, the population of the same type of tree is represented by the function\(B(t)=82(1.029)^t\). (Round answers to the nearest whole number.)

67) Which forest’s population is growing at a faster rate?

68) Which forest had a greater number of trees initially? By how many?

69) Assuming the population growth models continue to represent the growth of the forests, which forest will have a greater number of trees after \(20\) years? By how many?

70) Assuming the population growth models continue to represent the growth of the forests, which forest will have a greater number of trees after \(100\) years? By how many?

71) Discuss the above results from the previous four exercises. Assuming the population growth models continue to represent the growth of the forests, which forest will have the greater number of trees in the long run? Why? What are some factors that might influence the long-term validity of the exponential growth model?

Answers to odd exercises:

67. The forest represented by the function  \(B(t)=82(1.029)^t\). The growth rate is \(2.9\%\). The growth factor is \(1.029\).

69. After \(t=20\) years, forest A will have \(43\) more trees than forest B.

71. Answers will vary. Sample response: For a number of years, the population of forest A will increasingly exceed forest B, but because forest B actually grows at a faster rate, the population will eventually become larger than forest A and will remain that way as long as the population growth models hold. Some factors that might influence the long-term validity of the exponential growth model are drought, an epidemic that culls the population, and other environmental and biological factors.

E: Solve Exponential Applications Given a Formula

Exercise \(\PageIndex{E}\) 

73. The population of a certain small town is growing according to the function \(P (t) = 12,500(1.02)^{t}\) where \(t\) represents time in years since the last census. Use the function to determine the population on the day of the census (when \(t = 0\)) and estimate the population in \(6\) years from that time.

74. The population of a certain small town is decreasing according to the function \(P (t) = 22,300(0.982)^{t}\) where \(t\) represents time in years since the last census. Use the function to determine the population on the day of the census (when \(t = 0\)) and estimate the population in \(6\) years from that time.

75. The decreasing value, in dollars, of a new car is modeled by the formula \(V (t) = 28,000(0.84)^{t}\) where \(t\) represents the number of years after the car was purchased. Use the formula to determine the value of the car when it was new (\(t = 0\)) and the value after \(4\) years.

76. The number of unique visitors to the college website can be approximated by the formula \(N (t) = 410(1.32)^{t}\) where \(t\) represents the number of years after 1997 when the website was created. Approximate the number of unique visitors to the college website in the year 2020.

77. If left unchecked, a new strain of flu virus can spread from a single person to others very quickly. The number of people affected can be modeled using the formula \(P(t)=e^{0.22 t}\) where \(t\) represents the number of days the virus is allowed to spread unchecked. Estimate the number of people infected with the virus after \(30\) days and after \(60\) days.

78. If left unchecked, a population of \(24\) wild English rabbits can grow according to the formula \(P(t)=24 e^{0.19 t}\) where the time \(t\) is measured in months. How many rabbits would be present \(3 \frac{1}{2}\) years later?

79. The population of a certain city in 1975 was \(65,000\) people and was growing exponentially at an annual rate of \(1.7\)%. At the time, the population growth was modeled by the formula \(P (t) = 65,000e^{0.017t}\) where \(t\) represented the number of years since 1975. In the year 2000, the census determined that the actual population was \(104,250\) people. What population did the model predict for the year 2000 and what was the actual error?

80. Because of radioactive decay, the amount of a \(10\) milligram sample of Iodine-131 decreases according to the formula \(A (t) = 10e^{−0.087t}\) where \(t\) represents time measured in days. How much of the sample remains after \(10\) days?

81. The number of cells in a bacteria sample is approximated by the logistic growth model \(N(t)=\frac{1.2 \times 10^{5}}{1+9 e^{-0.32 t}}\) where \(t\) represents time in hours. Determine the initial number of cells and then determine the number of cells \(6\) hours later.

82. The market share of a product, as a percentage, is approximated by the formula \(P(t)=\frac{100}{2+e^{-0.44 t}}\) where \(t\) represents the number of months after an aggressive advertising campaign is launched. By how much can we expect the market share to increase after the first three months of advertising?

Answers to odd exercises:

73. Initial population: \(12,500\); Population \(6\) years later: \(14,077\)

75. New: $\(28,000\); In \(4\) years: $\(13,940.40\)

77. After \(30\) days: \(735\) people; After \(60\) days: \(540,365\) people

79. Model: \(99,423\) people; error: \(4,827\) people

81. Initially there are \(12,000\) cells and \(6\) hours later there are \(51,736\) cells.

F: Solve Exponential Application problems given a rate

Exercise \(\PageIndex{F}\) 

83) The fox population in a certain region has an annual growth rate of \(9\%\) per year. In the year 2012, there were \(23,900\) fox counted in the area. What is the equation that models this growth? What is the fox population predicted to be in the year 2020?

Answers to odd exercises: 

83. \(23900(1.09)^t\), \(47,622\) fox

G: Exponential Application problems find a rate

Exercise \(\PageIndex{G}\) 

84) A scientist begins with \(100\) milligrams of a radioactive substance that decays exponentially. After \(35\) hours, \(50\)mg of the substance remains. How many milligrams will remain after \(54\) hours?

85) In the year 1985, a house was valued at \(\$110,000\). By the year 2005, the value had appreciated to \(\$145,000\). What was the annual growth rate between 1985 and 2005? Assume that the value continued to grow by the same percentage. What was the value of the house in the year 2010?

86) A car was valued at \(\$38,000\) in the year 2007. By 2013, the value had depreciated to \(\$11,000\) If the car’s value continues to drop by the same percentage, what will it be worth by 2017?

Answers to odd exercises:

85. Growth factor \(b=1.0139\), Growth rate = \(1.39\%\); \(\$155,368.09\)

H: Construct the Formula \(f(x) = a (b)^x\) given Two Points

Exercise \(\PageIndex{H}\) 

\( \bigstar \) For the following exercises, find the formula for an exponential function \(y=a(b^x)\) that passes through the two points given.

88) (\(0,6)\) and  \((3,750)\) 89) \((0,2000)\)  \((2,20)\)

90) \(\left (−1,\frac{3}{2} \right )\) and \((3,24)\) 91) \( (−2,6)\)  \((3,1)\)

92) \((3,1)\) and \((5,4)\)

Answers to odd exercises:

89. \(f(x)=2000(0.1)^x\)

91. \(f(x)=\left ( \frac{1}{6} \right )^{-\frac{3}{5}} \left ( \frac{1}{6} \right )^{\frac{x}{5}}\approx 2.93 (0.699)^x\)

I: Construct a formula \(f(x) = a (b)^x\) given a Graph

Exercise \(\PageIndex{I}\) 

\( \bigstar \) Find an equation \(y=ab^x\) for the exponential functions graphed below.

93.	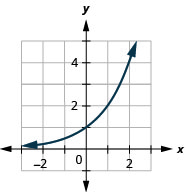94.	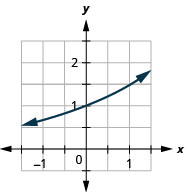95.
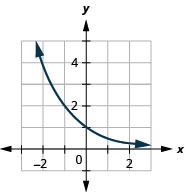96.	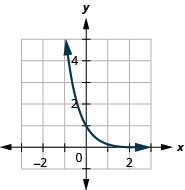97.	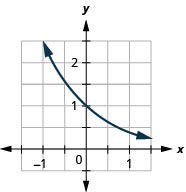98.

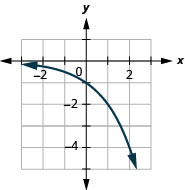Answers to odd exercises:

93. \(f(x)=2^{x}\)

95. \(f(x)=\left(\frac{1}{2}\right)^{x}\)

97. \(f(x)=(0.4)^{x}\)

J: Compound Interest

Exercise \(\PageIndex{J}\) 

\( \bigstar \) For the following exercises, use the compound interest formula, \(A(t)=P\left (1+ \frac{r}{n} \right )^{nt}\)

After a certain number of years, the value of an investment account is represented by the equation \(10,250\left (1+ \frac{0.04}{12} \right )^{120}\).

100) What is the value of the account?

101) What was the initial deposit made to the account in the previous exercise?

102) How many years had the account from the previous exercise been accumulating interest?

An account is opened with an initial deposit of \(\$6,500\) and earns \(3.6\%\) interest compounded semi-annually.

103) What will the account be worth in \(20\)years?

104) How much more would the account in the previous exercise be worth if the interest were compounding weekly?

105) Solve the compound interest formula for the principal, \(P\).

106) Use the formula found in the previous exercise to calculate the initial deposit of an account that is worth \(\$14,472.74\) after earning  \(5.5\%\) interest compounded monthly for \(5\) years. (Round to the nearest dollar.)

107) How much more would the account in the previous two exercises be worth if it were earning interest for \(5\) more years?

108) Use properties of rational exponents to solve the compound interest formula for the interest rate, \(r\).

109) Use the formula found in the previous exercise to calculate the interest rate for an account that was compounded semi-annually, had an initial deposit of \(\$9,000\) and was worth \(\$13,373.53\) after \(10\) years.

110) Use the formula found in the previous exercise to calculate the interest rate for an account that was compounded monthly, had an initial deposit of \(\$5,500\), and was worth \(\$38,455\) after \(30\) years.

111) Repeat the previous exercise to find the APY formula of an account that compounds daily. Use the results from this and the previous exercise to develop a function \(I(n)\) for the APY of any account that compounds \(n\) times per year.

112) The annual percentage yield (APY) of an investment account is a representation of the actual interest rate earned on a compounding account. It is based on a compounding period of one year. Show that the APY of an account that compounds monthly can be found with the formula  \(APY=\left (1+\frac{r}{12} \right )^{12}-1\)

113) Jamal wants to save \(\$54,000\) for a down payment on a home. How much will he need to invest in an account with \(8.2\%\) APR, compounding daily, in order to reach his goal in \(5\) years?

114) Kyoko has \(\$10,000\) that she wants to invest. Her bank has several investment accounts to choose from, all compounding daily. Her goal is to have \(\$15,000\) by the time she finishes graduate school in \(6\) years. To the nearest hundredth of a percent, what should her minimum annual interest rate be in order to reach her goal? (Hint: solve the compound interest formula for the interest rate.)

115. Jim invested $\(750\) in a \(3\)-year CD that earns \(4.2\)% annual interest that is compounded monthly. How much will the CD be worth at the end of the \(3\)-year term?

116. Jose invested $\(2,450\) in a \(4\)-year CD that earns \(3.6\)% annual interest that is compounded semi-annually. How much will the CD be worth at the end of the \(4\)-year term?

117. Jane has her $\(5,350\) savings in an account earning \(3 \frac{5}{8}\)% annual interest that is compounded quarterly. How much will be in the account at the end of \(5\) years?

118. Bill has $\(12,400\) in a regular savings account earning \(4 \frac{2}{3}\)% annual interest that is compounded monthly. How much will be in the account at the end of \(3\) years?

119. If $\(85,200\) is invested in an account earning \(5.8\)% annual interest compounded quarterly, then how much interest is accrued in the first \(3\) years?

120. If $\(124,000\) is invested in an account earning \(4.6\)% annual interest compounded monthly, then how much interest is accrued in the first \(2\) years?

Answers to odd exercises:

101. \(\$10,250\)          103. \(\$13,268.58\)          105. \(P=A(t)\cdot \left (1+ \frac{r}{n} \right )^{-nt}\)          107. \(\$4,569.10\)          109. \(4\%\)
111. \( APY = \frac{A(t)-a}{a} = \frac{a\left ( 1+\frac{r}{365} \right )^{365(1)}-a}{a} = \frac{a\left [\left ( 1+\frac{r}{365} \right )^{365}-1 \right ]}{a} = \left ( 1+\frac{r}{365} \right )^{365}-1 \)     \(I(n)=\left ( 1+\frac{r}{n} \right )^n - 1\)
113. \(\$35,838.76\)          115. $\(850.52\)          117. $\(6,407.89\)          119. $\(16,066.13\)

K: Continuous  Interest

Exercise \(\PageIndex{K}\) 

121. Bill invested $\(1,400\) in a \(3\)-year CD that earns \(4.2\)% annual interest that is compounded continuously. How much will the CD be worth at the end of the \(3\)-year term?

122. Brooklyn invested $\(2,850\) in a \(5\)-year CD that earns \(5.3\)% annual interest that is compounded continuously. How much will the CD be worth at the end of the \(5\)-year term?

123. Omar has his $\(4,200\) savings in an account earning \(4 \frac{3}{8}\)% annual interest that is compounded continuously. How much will be in the account at the end of \(2 \frac{1}{2}\) years?

124. Nancy has her $\(8,325\) savings in an account earning \(5 \frac{7}{8}\)% annual interest that is compounded continuously. How much will be in the account at the end of \(5 \frac{1}{2}\) years?

125. If $\(12,500\) is invested in an account earning \(3.8\)% annual interest compounded continuously, then how much interest is accrued in the first \(10\) years?

126. If $\(220,000\) is invested in an account earning \(4.5\)% annual interest compounded continuously, then how much interest is accrued in the first \(2\) years?

Answers to odd exercises:

121. $\(1,588.00\)

123. $\(4,685.44\)

125. $\(5,778.56\)

L: Continuous and Compounded Interest

Exercise \(\PageIndex{L}\) 

127) Suppose an investment account is opened with an initial deposit of \(\$12,000\) earning  \(7.2\%\) interest compounded monthly. How much will the account be worth after \(30\) years?

128) How much more would the account from the previous exercise be worth after \(30\) years if it were compounded continuously instead?

129) Alyssa opened a retirement account with \(7.25\%\) APR in the year 2000. Her initial deposit was \(\$13,500\). How much will the account be worth in 2025 if interest compounds monthly? How much more would she make if interest compounded continuously?

130) An investment account with an annual interest rate of \(7\%\) was opened with an initial deposit of \(\$4,000\) Compare the values of the account after \(9\) years when the interest is compounded annually, quarterly, monthly, and continuously.

Answers to odd exercises:

127. \(\$103,384.23\)

129. \(\$82,247.78\); \(\$449.75\)