5.4: The Other Trigonometric Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
In the previous section, we defined the sine and cosine functions as ratios of sides of a right triangle formed by the point of intersection
Definition: Sine, Cosine, Tangent, Secant, Cosecant, and Cotangent Functions
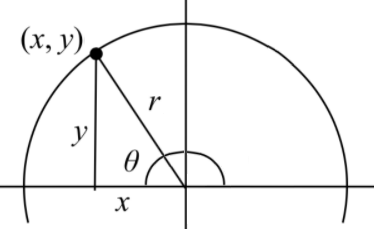 For the point (
For the point (
The signs that
Use Definitions to Obtain Trigonometric Function Values
If the coordinates of a point on the terminal side of an angle are known, the values of the trigonometric function can be found using the definitions.
Given a point on the terminal side of an angle.
Example
The point (-1, 7) is on the terminal side of some angle
Solution
We know a triangle is formed in the 2nd Quadrant, with sides
The Pythagorean Theorem can be used to find the third side:
Now the definitions of the six trigonometric functions can be used to obtain the desired function values.
Example
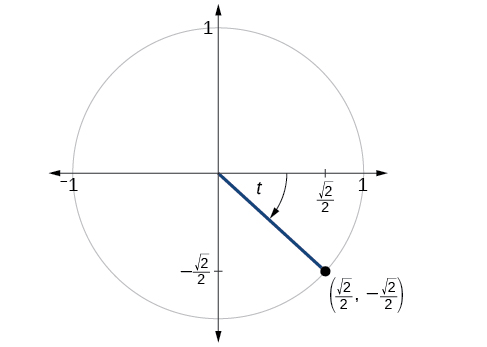
The point
Solution
Because this is a point on the unit circle,
![]() Try It
Try It
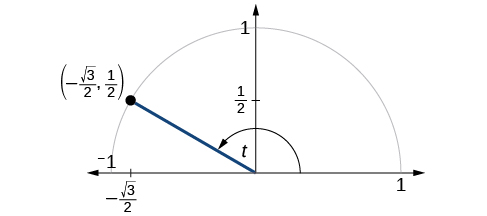
- Suppose the terminal side of
- The point
- Answers
-
1. Since
then2. We have
Given one trigonometric ratio, find other trigonometric ratios
When given a trigonometric ratio, it is possible to narrow down the possible quadrants the angle is in to two, based on the definition of the trigonometric ratio and the signs that
|
|
|
|
| Figure |
||
If given a trigonometric ratio, the definitions can be used 'in reverse' to determine the values of two of the three legs (
![]() How to: Find trig ratios given one trig ratio.
How to: Find trig ratios given one trig ratio.
Reference Triangle or Pythagorean Theorem Approach. Given a trigonometric ratio and perhaps some other information.
- Determine the quadrant the angle is in, and the signs of
- Use the definition of the given trigonometric function and the quadrant it is in to determine two of the three sides of a reference triangle and their appropriate signs.
- Use the Pythagorean Theorem to find the third side, and its appropriate sign. Now all three sides of the reference triangle are known.
- Use the definitions to determine the other trigonometric ratios.
Given a quadrant the angle is in
Example
Given
Solution
Step 1. Angle
Step 2.
Step 3. Find
Step 4. Using the definitions,
![]() Try It
Try It
Suppose
- Answers
-
We need to find a point
We have that
Using
Thus
Given a range of angle values
If a range of values an angle can have is given, that information can be translated to the quadrant the angle is in, and therefore the signs that
Figure
Example
- If
- If
Solution
1.
Find
Using the definitions,
2.
Find
Using the definitions,
![]() Try It
Try It
If
- Answers
-
Given the sign of another trigonometric ratio
Example
- If
- If
1. Solution
Step 1. Angle
Therefore
Step 2.
Step 3. Find
Step 4. Using the definitions,
2. Solution
Step 1. Angle
Therefore
Step 2.
Step 3. Find
Step 4. Using the definitions,
![]() Try It
Try It
If
- Answers
-
Given only one trigonometric ratio
Notice in the problems above we were given both a trigonometric ratio and the quadrant the angle was in. When the quadrant is not given, there are two possible solutions, as the example below illustrates.
Example
Given
Solution
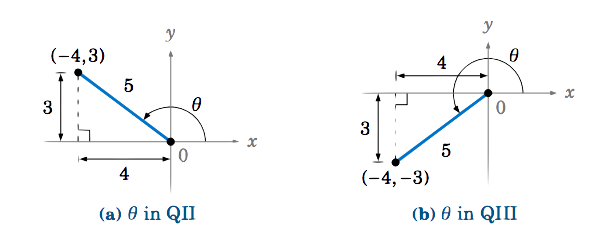
Given
Using the Pythagorean Theorem to determine
Thus there are actually two possible angles for
If the point
If the point
Trigonometric Function Values From Identities
Whenever a trigonometric ratio is given, and other function values are desired, there are two different approaches that can be used. We have been illustrating the use of the definitions and the Pythagorean Theorem. Another approach which will now be discussed uses identities.
Reciprocal and Quotient Identities
You may have noticed that the ratios defining the secant, cosecant, and cotangent are the reciprocals of the ratios defining the cosine, sine, and tangent functions, respectively. Additionally, notice that
Applying this concept to the other trigonometric functions we can state the Reciprocal and Quotient Identities.
Identities
| Reciprocal Identities | |||
| Quotient Identities |
These relationships are called identities. Identities are statements that are true for all values of the input on which they are defined. Identities are usually something that can be derived from definitions and relationships we already know.
Trigonometric Functions of Special Angles
Example
- Given
- Given
Solution
Because we know the sine and cosine values for these angles, we can use identities to evaluate the other functions.
Notice this result is consistent with our interpretation of the tangent value as the slope of the line passing through the origin at the given angle: a line at 45 degrees would indeed have a slope of 1.
We know the values of sine and cosine for "special" angles
Example
Find
Solution
We have previously used the properties of equilateral triangles to demonstrate that
A common mistake is that although
![]() Try It
Try It
- Find
- Find
- Answer
-
Because we know the sine and cosine values for the common first-quadrant angles, we can find the other four function values for those angles by rewriting the definitions of tangent, secant, cosecant, and cotangent in terms of sine and cosine and evaluating the resulting expressions. The results are shown in Table
| Angle | |||||
|---|---|---|---|---|---|
| Sine | 0 | 1 | |||
| Cosine | 1 | 0 | |||
| Tangent | 0 | 1 | Undefined | ||
| Cosecant | Undefined | 2 | 1 | ||
| Secant | 1 | 2 | Undefined | ||
| Cotangent | Undefined | 1 | 0 |
Pythagorean Identities
The Pythagorean Identity we learned earlier was derived from the Pythagorean Theorem and the definitions of sine and cosine. We can build new identities from previously established identities. For example, if we divide both sides of the Pythagorean Identity by cosine squared, we can create a new identity:
![]() Try It
Try It
Use a similar approach to establish that
- Answer
-
Identities: Alternate forms of the Pythagorean Identity
![]() How to: Given one trigonometric ratio, find other ratios.
How to: Given one trigonometric ratio, find other ratios.
Identities Approach. Given a trigonometric ratio and other information.
- Determine the quadrant the angle must be in, and thus the signs of the various trig ratios in that quadrant.
- Use identities to find the other trig ratios and their appropriate signs. Typically, use an identity to find the value of sine or cosine or their reciprocal functions, and then use other identities to find the rest of the trigonometric ratios.
Given a Trigonometric Ratio and a Quadrant
Example
If
Solution
There are two approaches to this problem, both of which work equally well.
Approach 1 (Use the Pythagorean Theorem)
Angle
Find
Using the definitions,
Approach 2 (Use Identities)
Use the
Since the angle is in the third quadrant, the cosine value will be negative so the secant value will also be negative. Keeping the negative result, and using definition of secant,
Example
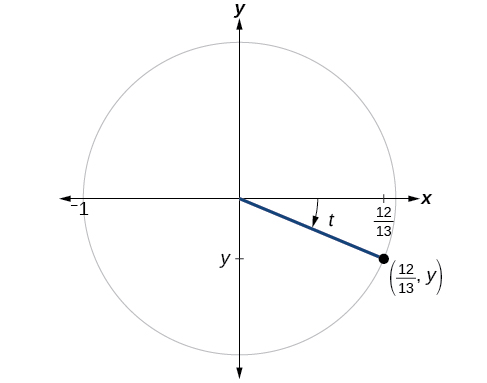
If
Solution
We are given the value of cosine so we can find the sine using the Pythagorean Identity,
The remaining functions can be calculated using identities relating them to sine and cosine.
![]() Try It
Try It
Evaluate
- Answer
-
Given
Trigonometric Function Values from Reference Angles
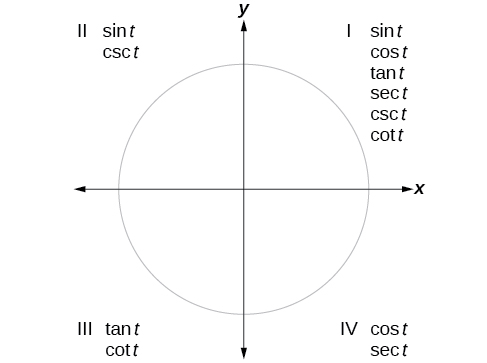
trigonometric functions are positive
We can evaluate trigonometric functions of angles outside the first quadrant using reference angles as we have already done with the sine and cosine functions. The procedure is the same: Find the reference angle formed by the terminal side of the given angle with the horizontal axis. The trigonometric function values for the original angle will be the same as those for the reference angle, except for the positive or negative sign, which is determined by x- and y-values in the quadrant where the terminal side is located.
Figure
To help us remember which of the six trigonometric functions are positive in each quadrant, we can use the mnemonic phrase “All Students Take Classes.” Each of the four words in the phrase corresponds to one of the four quadrants, starting with quadrant I and rotating counterclockwise. In quadrant I, which is “A,” all of the six trigonometric functions are positive. In quadrant II, “Students,” only sine and its reciprocal function, cosecant, are positive. In quadrant III, “Take,” only tangent and its reciprocal function, cotangent, are positive. Finally, in quadrant IV, “Classes,” only cosine and its reciprocal function, secant, are positive.
Example
Let
- Which angle between
- What is the reference angle for
- Draw these angles in standard position.
Solution
|
(a) Since
(b) |
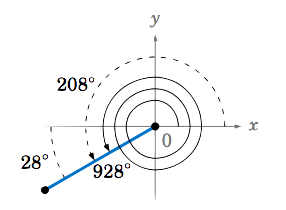 Figure |
Generalized Reference Angle Theorem
The absolute value of trigonometric functions of an angle
The choice of the (
![]() How to: Find Trigonometric Functions using Reference Angles.
How to: Find Trigonometric Functions using Reference Angles.
- Measure the angle formed by the terminal side of the given angle and the horizontal axis. This is the reference angle. The measure of a reference angle is ALWAYS a positive number between
- Observe the quadrant where the terminal side of the original angle is located. Based on the quadrant, determine whether the output is positive or negative. Rewrite the function in terms of the reference angle and the appropriate sign.
- Evaluate the function at the reference angle.
Example
Use reference angles to find all six trigonometric functions of
Solution
The angle between this angle’s terminal side and the x-axis is
![]() Try It
Try It
Use reference angles to find all six trigonometric functions of
- Answer
-
Angle
Example
Use Identities to determine the exact value of each of the following function values.
Solution
![]() Try It
Try It
Use Identities to determine the exact value of each of the following function values.
- Answer
-
Trigonometric Function Values from a Calculator
Values for the six trigonometric functions of "special" first-quadrant angles, and multiples of these angles that lie in other quadrants, can be evaluated using the value of the trig function for its reference angle and modifying the sign when appropriate.
For other angles, a calculator can be used to evaluate trigonometric functions. If the calculator has degree mode and radian mode, confirm the correct mode is chosen before making a calculation. There are calculator keys for SIN, COS, and TAN, but typically not for CSC, SEC, or COT. To evaluate these last three functions, the function must be evaluated as the reciprocal of a sine, cosine, or tangent function.
Example
- Use a calculator to find the cosecant of
1. Solution
- The angle is in radians so be sure the calculator is in radian mode.
- There is not a cosecant button on the calculator, so the reciprocal identity
- Enter the following keystrokes:
- The result obtained is
2. Solution
- The angle is in degrees so be sure the calculator is in degree mode.
- Enter the following keystrokes:
- The result is
- If the calculator does not have a degree mode, the angle must also be converted to radians. When the calculator only has a radian mode, enter the following keystrokes:
![]() Try It
Try It
Use a calculator to evaluate the following. Round to four decimal digits.
- Answer
-
Even and Odd Trigonometric Functions
To be able to use our six trigonometric functions freely with both positive and negative angle inputs, we should examine how each function treats a negative input. As it turns out, there is an important difference among the functions in this regard. Recall in Section 2.2: Attributes of Functions, even and odd functions were defined. This definition is repeated here.
Definition: Odd and Even functions
- An even function is one in which
- An odd function is one in which
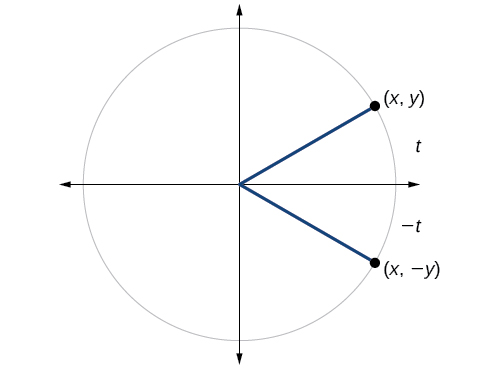
We can test whether a trigonometric function is even or odd by drawing a unit circle with a positive and a negative angle, as illustrated in Figure
- The sine of the positive angle is
- The cosine of the positive angle is
- The tangent of the positive angle is
Similar arguments can be made for the secant, cosecant and cotangent functions.
Even and Odd Trigonometric Functions; Even/Odd Identities
Cosine and secant are even functions:
Sine, tangent, cosecant, and cotangent are odd functions:
Example
If
Solution
Secant is an even function. The secant of an angle is the same as the secant of its opposite. So if the secant of angle t is 2, the secant of
![]() Try It
Try It
If the cotangent of angle
- Answer
Cofunction Identities
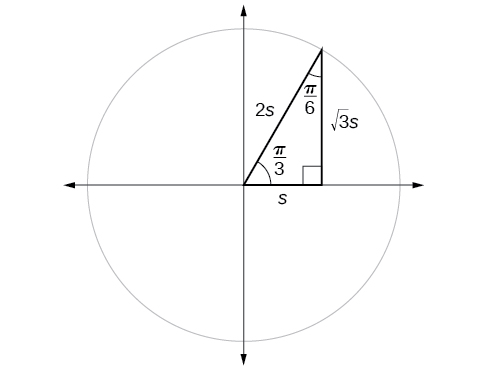
the cosine of
If we look more closely at the relationship between the sine and cosine of the special angles relative to the unit circle, we will notice a pattern. In a right triangle with angles of
This result should not be surprising because, as we see from Figure
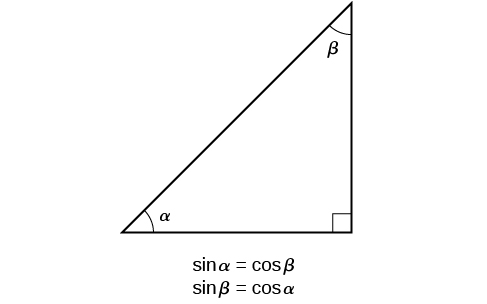
The interrelationship between the sines and cosines of
Using this identity, we can state without calculating, for instance, that the sine of
Cofunction Identities
The cofunction identities in terms of radians are listed below.
Example
If
Solution
According to the cofunction identities for sine and cosine,
![]() Try It
Try It
If
- Answer
- 2
Key Equations
| Tangent function | |
| Secant function | |
| Cosecant function | |
| Cotangent function |
| Reciprocal Identities | |||
| Quotient Identities | |||
| Pythagorean Identities | |||
| Even/Odd Identities | |||
| Cofunction Identities | |
Key Concepts
- The tangent of an angle is the ratio of the y-value to the x-value of the corresponding point on the unit circle.
- The secant, cotangent, and cosecant are all reciprocals of other functions. The secant is the reciprocal of the cosine function, the cotangent is the reciprocal of the tangent function, and the cosecant is the reciprocal of the sine function.
- The six trigonometric functions can be found from a point on the unit circle.
- Trigonometric functions can also be found from an angle.
- Trigonometric functions of angles outside the first quadrant can be determined using reference angles.
- The Pythagorean Identity makes it possible to find a cosine from a sine or a sine from a cosine.
- Identities can be used to evaluate trigonometric functions.
- Fundamental identities such as the Pythagorean Identity can be manipulated algebraically to produce new identities.
- The values of trigonometric functions of special angles can be found by mathematical analysis.
- To evaluate trigonometric functions of other angles, we can use a calculator or computer software.
- A function is said to be even if
- Cosine and secant are even; sine, tangent, cosecant, and cotangent are odd.
- Even and odd properties can be used to evaluate trigonometric functions.
Glossary
- cosecant
- the reciprocal of the sine function: on the unit circle,
- cotangent
- the reciprocal of the tangent function: on the unit circle,
- identities
- statements that are true for all values of the input on which they are defined
- secant
- the reciprocal of the cosine function: on the unit circle,
- tangent
- the quotient of the sine and cosine: on the unit circle,
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.

