6.4e: Exercises - Sum and Difference Identities
- Page ID
- 74425
A: Evaluate sum and difference formulas from a given angle.
Exercise \(\PageIndex{A}\)
\( \bigstar \) Find the exact value.
|
1. \( \cos \left ( \dfrac{7\pi }{4}- \dfrac{5\pi }{3} \right) \\[4pt]\) 2. \( \cos \left ( \dfrac{11\pi }{6}- \dfrac{3\pi }{4} \right) \\[4pt]\) 3. \( \cos \left ( \dfrac{\pi }{4}+ \dfrac{2\pi }{3} \right) \\[4pt]\) 4. \( \cos \left ( \dfrac{5\pi }{4}+ \dfrac{\pi }{3} \right) \\[4pt]\) |
5. \( \sin \left ( \dfrac{5\pi }{4}- \dfrac{7\pi }{6} \right) \\[4pt]\) 6. \( \sin \left ( \dfrac{5\pi }{3}- \dfrac{3\pi }{4} \right) \\[4pt]\) 7. \( \sin \left ( \dfrac{\pi }{4}+ \dfrac{5\pi }{6} \right) \\[4pt]\) 8. \( \sin \left ( \dfrac{7\pi }{4}+ \dfrac{\pi }{6} \right) \\[4pt]\) |
9. \( \tan \left ( \dfrac{11\pi }{6}- \dfrac{5\pi }{4} \right) \\[4pt]\) 10. \( \tan \left ( \dfrac{7\pi }{4}- \dfrac{2\pi }{3} \right) \\[4pt]\) 11. \( \tan \left ( \dfrac{\pi }{4}+ \dfrac{\pi }{6} \right) \\[4pt]\) 12. \( \tan \left ( \dfrac{3\pi }{4}+ \dfrac{7\pi }{6} \right) \\[4pt]\) |
\( \bigstar \) Find the exact value.
|
13. \( \cos \left (\dfrac{\pi }{12} \right) = \cos \left ( \dfrac{4\pi }{3}- \dfrac{5\pi }{4} \right) \\[4pt] \) 14. \(\cos \left (\dfrac{7\pi }{12} \right) = \cos \left ( \dfrac{5\pi }{6}- \dfrac{\pi }{4} \right) \\[4pt] \) 15. \( \sin \left (\dfrac{11\pi }{12} \right) = \sin \left ( \dfrac{3\pi }{4}+ \dfrac{\pi }{6} \right) \) |
16. \(\sin \left (\dfrac{5\pi }{12} \right) = \sin \left ( \dfrac{7\pi }{4}- \dfrac{4\pi }{3} \right) \\[4pt] \) 17. \(\tan \left (\dfrac{19\pi }{12} \right) = \tan \left ( \dfrac{3\pi }{4}+ \dfrac{5\pi }{6} \right) \\[4pt]\) 18. \(\tan \left (-\dfrac{\pi }{12} \right) = \tan \left ( \dfrac{7\pi }{6}- \dfrac{5\pi }{4} \right) \) |
19. \(\sin (195^{\circ}) \) 20. \(\sin (75^{\circ}) \) 21. \(\cos (345^{\circ}) \) 22. \(\cos (165^{\circ}) \) 23. \(\tan (-15^{\circ}) \) 24. \(\cos (105^{\circ}) \) |
\( \bigstar \) Simplify
| 25. \(\sin \left (x-\dfrac{3\pi }{4} \right)\) | 26. \(\sin \left (x+\dfrac{11\pi }{6} \right)\) | 27. \(\cos \left (x+\dfrac{2\pi }{3} \right)\) | 28. \(\cos \left (x-\dfrac{5\pi }{6} \right)\) |
| 29. \(\sec \left (\dfrac{\pi }{2}-\theta \right)\) | 30. \(\csc \left (\dfrac{\pi }{2}-t \right)\) | 31. \(\cot \left (\dfrac{\pi }{2}-x \right)\) | 32. \(\tan \left (\dfrac{\pi }{4}-x \right)\) |
\( \bigstar \) (a) Simplify and then (b) graph
|
33. \(\cos \left ( \dfrac{\pi }{2}-x \right )\) 34. \(\sin (\pi -x)\) |
35. \(\tan \left ( \dfrac{\pi }{3}+x \right )\) 36. \(\sin \left ( \dfrac{\pi }{3}+x \right )\) |
37. \(\tan \left ( \dfrac{\pi }{4}-x \right )\) 38. \(\cos \left ( \dfrac{7\pi }{6}+x \right )\) |
39. \(\sin \left ( \dfrac{\pi }{4}+x \right )\) 40. \(\cos \left ( \dfrac{5\pi }{4}+x \right )\) |
- Answers to odd exercises.
-
1. \(\dfrac{\sqrt{2}+\sqrt{6}}{4}\) 3. \(\dfrac{-\sqrt{2}-\sqrt{6}}{4}\) 5. \(\dfrac{\sqrt{6}-\sqrt{2}}{4}\) 7. \(\dfrac{\sqrt{2}-\sqrt{6}}{4}\) 9. \( -2 - \sqrt{3} \) 11. \( 2 + \sqrt{3} \)
13. \(\dfrac{\sqrt{2}+\sqrt{6}}{4}\) 15. \(\dfrac{\sqrt{6}-\sqrt{2}}{4}\) 17. \(-2-\sqrt{3}\) 19. \(-\dfrac{\sqrt{3}-1}{2\sqrt{2}}\) 21. \(\dfrac{1+\sqrt{3}}{2\sqrt{2}}\) 23. \( -2 + \sqrt{3} \)
25. \(-\dfrac{\sqrt{2}}{2}\sin x-\dfrac{\sqrt{2}}{2}\cos x\) 27. \(-\dfrac{1}{2}\cos x-\dfrac{\sqrt{3}}{2}\sin x\) 29. \(\csc \theta\) 31. \(\tan x\)
33. \(\sin x\)
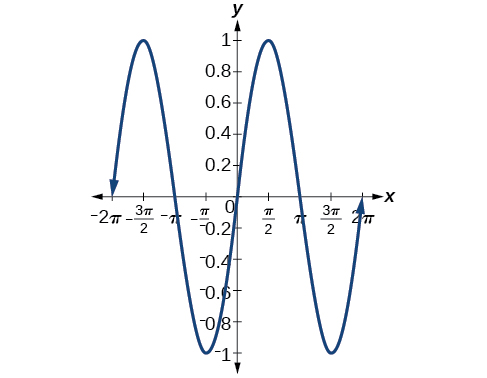
35. \(\cot \left ( \dfrac{\pi }{6}-x \right )\)
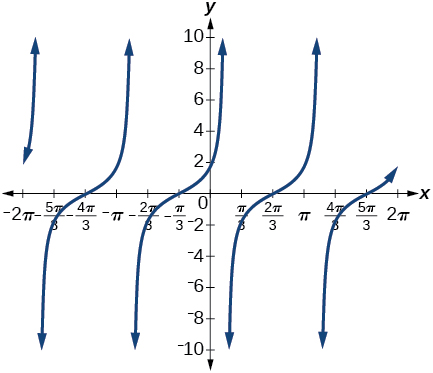
37. \(\cot \left ( \dfrac{\pi }{4}+x \right )\)
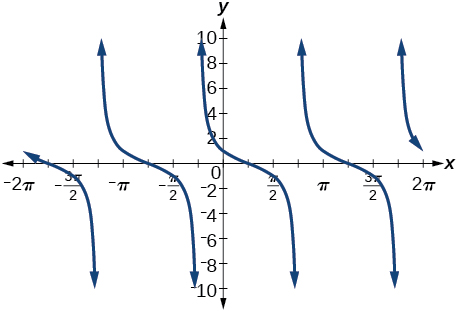
39. \(\dfrac{\sin x}{\sqrt{2}}+\dfrac{\cos x}{\sqrt{2}}\)
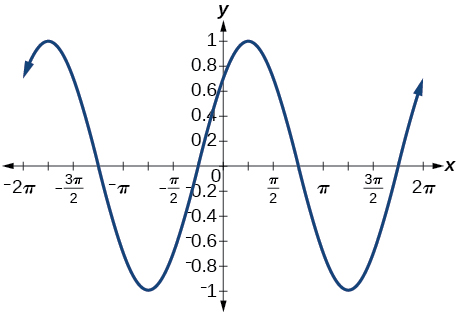
B: Evaluate sum and difference formulas given trig ratios of angles
Exercise \(\PageIndex{B}\)
41. Given that \(\sin a=\dfrac{4}{5}\) and \(\cos b=\dfrac{1}{3}\), with \(a\) and \(b\) both in the interval \(\left [ 0, \dfrac{\pi }{2} \right )\)
(a) Find \(\sin (a-b)\) (b) Find \(\cos (a+b)\).
42. Given that \(\sin a=\dfrac{2}{3}\) and \(\cos b=-\dfrac{1}{4}\) with \(a\) and \(b\) both in the interval \(\left [ \dfrac{\pi }{2}, \pi \right )\)
(a) Find \(\sin (a+b)\) (b) Find \(\cos (a-b)\).
43. Angles \(A\) and \(B\) are in standard position and \(\sin( A ) = \dfrac{1}{2}, \cos(A) > 0)\), \(\cos(B) = \dfrac{3}{4}\), and \(\sin(B) < 0\).
Draw a picture of the angles \(A\) and \(B\) in the plane and then find each of the following.
(a) \(\cos(A + B)\) (b) \(\cos(A - B)\) (c) \(\sin(A + B)\) (d) \(\sin(A - B)\) (e) \(\tan(A + B)\) (f) \(\tan(A - B)\)
\( \bigstar \) Given the information about angles \(A\) and \(B\) in the exercises below, find the exact value for each of the following.
(a) \(\cos(A + B)\) (b) \(\cos(A - B)\) (c) \(\sin(A + B)\) (d) \(\sin(A - B)\) (e) \(\tan(A + B)\) (f) \(\tan(A - B)\)
45. \( \sin A = -\dfrac{3}{5} \) with \(A\) in Quadrant III, and \( \cos B = \dfrac{1}{2} \) with \(B\) in Quadrant IV.
46. \( \sin A = \dfrac{4}{5} \) with \(A\) in Quadrant I, and \( \tan B = -\dfrac{\sqrt{5}}{2} \) with \(B\) in Quadrant II.
47. \( \cos A = \dfrac{1}{2} \) with \( 0 \le A \le \tfrac{\pi}{2} \), and \( \tan B = 2 \sqrt{2} \) with \( \pi \le B \le \tfrac{3\pi}{2} \).
48. \( \cos A = -\dfrac{\sqrt{3}}{3} \) with \( \pi \le A \le \tfrac{3\pi}{2} \), and \( \sin B = \dfrac{\sqrt{3}}{3} \) with \(\tfrac{\pi}{2} \le B \le \pi \).
49. \( A = \tan^{-1} \left( \sqrt{5} \right) \) and \( B = \sin^{-1} \left( - \dfrac{\sqrt{5}}{3} \right) \)
50. \( A = \tan^{-1} \left( - 2 \right) \) and \( B = \cos^{-1} \left( - \dfrac{\sqrt{6}}{6} \right) \)
\( \bigstar \) Find the exact value of each expression.
|
52. |
53. |
54. |
|
|
|
|
- Answers to odd exercises.
-
41a. \(\sin (a-b)=\left ( \frac{4}{5} \right )\left ( \frac{1}{3} \right )-\left ( \frac{3}{5} \right )\left ( \frac{2\sqrt{2}}{3} \right )=\dfrac{4-6\sqrt{2}}{15}\)
41b. \(\cos (a+b)=\left ( \frac{3}{5} \right )\left ( \frac{1}{3} \right )-\left ( \frac{4}{5} \right )\left ( \frac{2\sqrt{2}}{3} \right )=\dfrac{3-8\sqrt{2}}{15}\)
43. a. \( \tfrac{\sqrt{3}}{2} \cdot \tfrac{3}{4} - \tfrac{1}{2} \cdot \tfrac{-\sqrt{7}}{4} =\dfrac{3\sqrt{3} + \sqrt{7}}{8}\), b. \( \dfrac{3\sqrt{3} - \sqrt{7}}{8}\), c. \( \dfrac{3 - \sqrt{21}}{8}\), d. \( \dfrac{3 + \sqrt{21}}{8}\), e. \(\dfrac{4\sqrt{3} -3 \sqrt{7}}{5}\), f. \(\dfrac{4\sqrt{3} +3 \sqrt{7}}{5}\)
45. \( \sin (A+B) = \tfrac{-3}{5} \cdot \tfrac{1}{2} + \tfrac{-4}{5} \cdot \tfrac{-\sqrt{3}}{2} = \dfrac{-3+4\sqrt{3}}{10} \), \( \cos(A+B) = \dfrac{-4-3\sqrt{3}}{10} \), \( \tan(A+B) = \dfrac{48 - 25\sqrt{3}}{-11} \\ \)
\( \quad \;\; \sin(A-B) = \dfrac{-3-4\sqrt{3}}{10} \), \( \cos(A-B) = \dfrac{-4+3\sqrt{3}}{10} \), \( \tan(A-B) = \dfrac{48 + 25\sqrt{3}}{-11} \)47. \( \sin (A+B) = \tfrac{\sqrt{3}}{2} \cdot \tfrac{-1}{3} + \tfrac{1}{2} \cdot \tfrac{-2\sqrt{2}}{3} = \dfrac{-\sqrt{3}-2\sqrt{2}}{6}\), \( \cos(A+B) = \dfrac{-1+2\sqrt{6}}{6}\), \( \tan(A+B) = \dfrac{-9\sqrt{3} - 8\sqrt{2}}{23} \\ \)
\( \quad \;\; \sin(A-B) = \dfrac{-\sqrt{3}+2\sqrt{2}}{6} \), \( \cos(A-B) = \dfrac{-1-2\sqrt{6}}{6}\), \( \tan(A-B) = \dfrac{-9\sqrt{3} + 8\sqrt{2}}{23} \)49. \( \sin (A+B) = \tfrac{\sqrt{3}}{6} \cdot \tfrac{2}{3} + \tfrac{\sqrt{6}}{6} \cdot \tfrac{-\sqrt{5}}{3} = \dfrac{\sqrt{30}}{18},\) \( \cos(A+B) = \dfrac{7\sqrt{6}}{18},\) \( \tan(A+B) = \dfrac{\sqrt{5}}{7} \\ \)
\( \quad \;\; \sin(A-B) = \dfrac{\sqrt{30}}{6}\), \( \cos(A-B) = \dfrac{-\sqrt{6}}{6}\), \( \tan(A-B) = -\sqrt{5} \)53. \(\dfrac{\sqrt{2}-\sqrt{6}}{4}\) 59. \( \dfrac{\sqrt{1-u^4} -u^2 \sqrt{1+u^2} }{1+u^2} \)
C: Solve Equations
Exercise \(\PageIndex{D}\)
\( \bigstar \) Solve each equation for all solutions.
|
65. \(\sin \left(3x\right)\cos \left(6x\right)-\cos \left(3x\right)\sin \left(6x\right)= -0.9\) 66. \(\sin \left(6x\right)\cos \left(11x\right)-\cos \left(6x\right)\sin \left(11x\right)= -0.1\) |
67. \(\cos \left(2x\right)\cos \left(x\right)+\sin \left(2x\right)\sin \left(x\right)=1\) 68. \(\cos \left(5x\right)\cos \left(3x\right)-\sin \left(5x\right)\sin \left(3x\right)=\dfrac{\sqrt{3} }{2}\) |
- Answers to odd exercises.
-
65. \(0.373 + \frac{2\pi}{3} k\) and \(0.674 + \frac{2\pi}{3} k\), where \(k\) is an integer 67. \(2 \pi k\), where \(k\) is an integer
D: Verify Identities
Exercise \(\PageIndex{F}\)
\( \bigstar \) Simplify.
| 71. \(\dfrac{\tan \left (\dfrac{3}{2}x \right)-\tan \left (\dfrac{7}{5}x \right)}{1+\tan \left (\dfrac{3}{2}x \right)\tan \left (\dfrac{7}{5}x \right)}\) | 72. \(\sin(2x)\cos(5x)-\sin(5x)\cos(2x)\) |
\( \bigstar \) Verify the Identity.
|
73. \(\dfrac{\sin \left(x\right)+\sin \left(y\right)}{\cos \left(x\right)+\cos \left(y\right)} =\tan \left(\dfrac{1}{2} \left(x+y\right)\right)\) 74. \(\dfrac{\sin\;(A-B)}{\sin\;(A+B)} ~=~ \dfrac{\cot\;B \;-\; \cot\;A}{\cot\;B \;+\; \cot\;A}\) 75. \(\cot\;A ~+~ \cot\;B ~=~ \dfrac{\sin\;(A+B)}{\sin\;A~\sin\;B}\) 76. \(\dfrac{\sin(r + s)}{\cos(r)\cos(s)} = \tan(r) + \tan(s)\) 77. \(\dfrac{\sin(r - s)}{\cos(r)\cos(s)} = \tan(r) - \tan(s)\) 78. \(\dfrac{\cos\;(A+B)}{\sin\;A~\cos\;B} ~=~ \cot\;A \;-\; \tan\;B\) 79. \(\dfrac{\cos (a+b)}{\cos a \cos b}=1-\tan a \tan b\) |
80. \(\dfrac{\tan (a+b)}{\tan (a-b)}=\dfrac{\sin a \cos a + \sin b \cos b}{\sin a \cos a - \sin b \cos b}\) 81. \(\tan \left ( x+\dfrac{\pi }{4} \right )=\dfrac{\tan x+1}{1-\tan x}\) 82. \(\tan \left(\dfrac{\pi }{4} -t\right)=\dfrac{1-\tan \left(t\right)}{1+\tan \left(t\right)}\) 83. \(\dfrac{\tan (x+y)}{1+\tan x \tan y}=\dfrac{\tan x + \tan y}{1-\tan^2 x \tan^2 y}\) 84. \(\cot\;(A+B) ~=~ \dfrac{\cot\;A~\cot\;B \;-\; 1}{\cot\;A \;+\; \cot\;B}\) 85. \(\cot\;(A-B) ~=~ \dfrac{\cot\;A~\cot\;B \;+\; 1}{\cot\;B \;-\; \cot\;A}\) 87. \(\dfrac{\cos(x+h)-\cos(x)}{h}=\cos x\dfrac{\cos (h)-1}{h}-\sin x \dfrac{\sin (h)}{h}\) |
- Answers to odd exercises
- 71. \(\tan \left (\frac{x}{10} \right) \)
75. \(\cot\;A ~+~ \cot\;B = \dfrac{\cos(A)}{\sin(A)} + \dfrac{\cos(B)}{\sin(B)} \\
= \dfrac{\cos(A)}{\sin(A)} \cdot \dfrac{\sin(B)}{\sin(B)} + \dfrac{\cos(B)}{\sin(B)} \cdot \dfrac{\sin(A)}{\sin(A)} \\ \)
\( \quad \;\;
= \dfrac{\cos(A)\sin(B) + \cos(B) \sin(A) }{\sin(A) \sin(B) } = \dfrac{\sin\;(A+B)}{\sin\;A~\sin\;B}\)
77. \(\dfrac{\sin(r - s)}{\cos(r)\cos(s)} = \dfrac{\sin (r) \cos (s) - \cos (r) \sin (s)}{\cos(r)\cos(s)}
\\ \)
\( \quad \;\;
=\dfrac{\sin (r) \cos (s)}{\cos(r)\cos(s)} - \dfrac{\cos (r) \sin (s)}{\cos(r)\cos(s)}
=\dfrac{\sin (r) }{\cos(r)} - \dfrac{ \sin (s)}{\cos(s)} = \tan(r) - \tan(s)\)
79. \( \dfrac{\cos (a+b)}{\cos a \cos b} = \dfrac{\cos a \cos b}{\cos a \cos b}- \dfrac{\sin a \sin b}{\cos a \cos b}= 1-\tan a \tan b \)
81. \( \tan \left ( x+\dfrac{\pi }{4} \right ) = \dfrac{\tan x + \tan\left (\tfrac{\pi}{4} \right )}{1-\tan x \tan\left (\tfrac{\pi}{4} \right )} = \dfrac{\tan x+1}{1-\tan x(1)} = \dfrac{\tan x+1}{1-\tan x} \)
83. \(\dfrac{\tan (x+y)}{1+\tan x \tan y}= \dfrac{\tan x + \tan y}{1- \tan x \tan y} \cdot \dfrac{1}{1+\tan x \tan y} = \dfrac{\tan x + \tan y}{1-\tan^2 x \tan^2 y}\)
85. \(\cot\;(A-B) = \dfrac{1}{\tan (A-B)}
=\dfrac{1+\tan A \tan B}{\tan A + \tan B}
=\dfrac{1+\tan A \tan B}{\tan A + \tan B} \cdot \dfrac{\cot A \cot B}{\cot A \cot B}
= \dfrac{\cot\;A~\cot\;B \;+\; 1}{\cot\;B \;-\; \cot\;A}\)
87. \( \dfrac{\cos(x+h)-\cos(x)}{h} = \dfrac{\cos x\cos (h) - \sin x\sin (h) -\cos x}{h} = \dfrac{\cos x(\cos (h)-1) - \sin x(\sin (h))}{h} \\ \)
\( \quad \;\; = \cos x \cdot \dfrac{\cos (h)-1}{h}-\sin x \cdot \dfrac{\sin (h)}{h} \)
\( \bigstar \) Verify the Identity.
|
90. \(2\sin \left(a+b\right)\sin \left(a-b\right)=\cos \left(2b\right)-{\rm cos}(2a)\) 91. \(\cos(x+y)\cos(x-y)=\cos^2x-\sin^2y\) 92. \(\cos \left(a+b\right)+\cos \left(a-b\right)=2\cos \left(a\right)\cos \left(b\right)\) 93. \( \sin(4x)-\sin(3x)\cos x =\sin x \cos(3x) \) 94. \( \cos(4x)+\sin x \sin(3x) = \cos x \cos(3x)\) 95. \( \sin(3x)\cos(6x)=\sin(9x)-\cos(3x)\sin(6x)\) 96. \( \sin(4x) = \sin(5x)\cos x-\cos(5x)\sin x \) |
97. \(\sin(3x)=3\sin x \cos^2x-\sin^3x \) 98. \(\cos(3x)=\cos^3x-3\sin^2x\cos x \) 99. \( \sin(2x) = 2 \sin x \cos x\) 100. \( \cos(2\theta ) = \cos^2\theta -\sin^2\theta\) 101. \( \tan(2\theta ) = \dfrac{2\tan \theta }{1-\tan^2\theta }\) 102. \( \tan(-x)=\dfrac{\tan x-\tan(2x)}{1+\tan x \tan(2x)} \) |
- Answers to odd exercises.
- 91. \(\cos(x+y)\cos(x-y) =(\cos x \cos y - \sin x \sin y)(\cos x \cos y + \sin x \sin y)
=\cos^2 x \cos^2 y - \sin ^2 x \sin ^2 y \)
\( \quad \;\; =(1-\sin^2 x )(1-\sin^2 y) - \sin ^2 x \sin ^2 y
=1 -\sin^2 x -\sin^2 y+\sin ^2 x \sin ^2 y - \sin ^2 x \sin ^2 y \)
\( \quad \;\;
=1 -\sin^2 x -\sin^2 y = \cos^2x-\sin^2y\)
93. \( \sin(4x)-\sin(3x)\cos x = \sin (x + 3x) -\sin(3x)\cos x \)
\( \quad \;\;
= \sin x \cos (3x) + \cos x \sin (3x) -\sin(3x)\cos x = \sin x \cos(3x) \)
95. \( \sin(3x)\cos(6x) = \sin(3x)\cos(6x) + \cos(3x)\sin(6x) -\cos(3x)\sin(6x) = \sin(9x)-\cos(3x)\sin(6x)\)
97. \( \sin (x+2x) = \sin x \cos (2x)+\sin (2x) \cos x = \sin x(\cos ^2 x - \sin ^2 x)+2\sin x \cos x \cos x \\
= \sin x \cos ^2 x-\sin ^3 x + 2\sin x\cos ^2 x = 3\sin x\cos ^2 x - \sin ^3 x \)
99. \( \sin(2x) = \sin x \cos x + \cos x \sin x = 2 \sin x \cos x\)
101. \( \tan(2\theta ) = \dfrac{ \tan \theta + \tan \theta}{1- \tan \theta \tan \theta} = \dfrac{2\tan \theta }{1-\tan^2\theta } \)

