6.5: Double-Angle, Half-Angle, and Reduction Formulas

Learning Objectives.

• Use double-angle formulas to find exact values
• Use double-angle formulas to solve equations
• Use double-angle formulas to verify identities
• Use reduction formulas to simplify an expression
• Use half-angle formulas to find exact values

Use Double-Angle Formulas to Find Exact Values

In the previous section, we used addition and subtraction formulas for trigonometric functions. Now, we take another look at those same formulas. The double-angle formulas are a special case of the sum formulas, where $\alpha=\beta$. Deriving the double-angle formula for sine begins with the sum formula,

$$\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta \nonumber$$

If we let $\alpha=\beta=\theta$, then we have

$sin(2\theta) =  \sin(\theta+\theta) = \sin \theta \cos \theta+\cos \theta \sin \theta\ = 2\sin \theta \cos \theta$

Deriving the double-angle for cosine gives us three options. First, starting from the sum formula, $\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta$, and letting $\alpha=\beta=\theta$, we have

$cos(2\theta) = \cos(\theta+\theta) = \cos \theta \cos \theta - \sin \theta \sin \theta = {\cos}^2 \theta - {\sin}^2 \theta$

Using the Pythagorean properties, we can expand this double-angle formula for cosine and get two more variations. The first variation is:

$\cos(2\theta) = {\cos}^2 \theta-{\sin}^2 \theta = (1-{\sin}^2 \theta)-{\sin}^2 \theta = 1 - 2 \sin^2 \theta$

The second variation is:

$\cos(2\theta) = {\cos}^2 \theta-{\sin}^2 \theta = \cos^2 \theta - (1-{\cos}^2 \theta) = 2 \cos^2 \theta - 1$

Similarly, to derive the double-angle formula for tangent, replacing $\alpha=\beta=\theta$ in the sum formula gives

$$\begin{align*} \tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\[4pt] \tan(\theta+\theta)&= \dfrac{\tan \theta+\tan \theta}{1-\tan \theta \tan \theta}\\[4pt] \tan(2\theta)&= \dfrac{2\tan \theta}{1-{\tan}^2 \theta} \end{align*}$$

DOUBLE-ANGLE FORMULAS

$$\begin{align} \sin(2\theta)&= 2 \sin \theta \cos \theta\\[4pt] \cos(2\theta)&= \begin{cases}{\cos}^2 \theta-{\sin}^2 \theta   \\  1-2 {\sin}^2 \theta   \\   2{\cos}^2 \theta-1 \end{cases}\\[4pt] \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2\theta} \end{align}$$

Example $\PageIndex{1}$: Use Double-Angle Formulas to Evaluate a Trigonometric Expression

Given that $\tan \theta=−\dfrac{3}{4}$ and $\theta$ is in quadrant II, find the following:

a. $\sin(2\theta)$ $\qquad$  b. $\cos(2\theta)$ $\qquad$ c. $\tan(2\theta)$

Solution

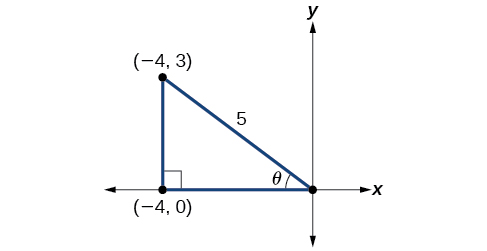If we draw a triangle to reflect the information given, we can find the values needed to solve the problems on the image. We are given $\tan \theta=−\dfrac{3}{4}$, such that $\theta$ is in quadrant II. The tangent of an angle is equal to the opposite side over the adjacent side, and because $\theta$ is in the second quadrant, the adjacent side is on the x-axis and is negative. Use the Pythagorean Theorem to find the length of the hypotenuse:

$c^2 = {(-4)}^2+{(3)}^2 = 16+9 = 25 \rightarrow c= 5$ Therefore,   ${ \begin{matrix} \boxed { \begin{array}{llr} x &=& -4 \\ y &=& 3\\ r &=& 5 \end{array}} \end{matrix} }$. 

Using these values we obtain:  ${ \begin{matrix} \boxed { \begin{array}{llr}\cos \theta &=& -\dfrac{4}{5}\\  \sin \theta &=& \dfrac{3}{5}\\ \tan \theta &=& -\dfrac{3}{4} \end{array} } \end{matrix} }$.

1. Write the double-angle formula for sine. Then substitute the values found above and simplify:

$$\begin{align*} \sin(2\theta)&=2 \sin \theta \cos \theta \\[4pt] & = 2\left(\dfrac{3}{5}\right)\left(-\dfrac{4}{5}\right)      \quad = -\dfrac{24}{25} \end{align*}$$

2. Write the double-angle formula for cosine.  Then substitute the values found above and simplify:

   $$\begin{align*} \cos(2\theta)&={\cos}^2 \theta−{\sin}^2 \theta  \\[4pt] &=    {\left(-\dfrac{4}{5}\right)}^2-{\left(\dfrac{3}{5}\right)}^2 \quad =\dfrac{16}{25}-\dfrac{9}{25} = \dfrac{7}{25} \end{align*}$$

3. Write the double-angle formula for tangent. Then substitute the values found above and simplify:

   $$\begin{align*} \tan(2\theta) &==\dfrac{2 \tan \theta}{1−{\tan}^2\theta}\\[4pt] &= \dfrac{2\left(-\dfrac{3}{4}\right )}{1-{\left(-\dfrac{3}{4}\right)}^2} \qquad = \dfrac{-\dfrac{3}{2}}{1-\dfrac{9}{16}}= -\dfrac{3}{2}\left(\dfrac{16}{7}\right)= -\dfrac{24}{7} \end{align*}$$

 Try It $\PageIndex{1}$

Given $\sin \alpha=\dfrac{5}{8}$, with $\theta$ in quadrant I, find $\cos(2\alpha)$. 

Answer

$\cos(2\alpha)=\dfrac{7}{32}$

Example $\PageIndex{2}$: Use Double-Angle Formulas to Rewrite Trigonometric Expressions

Use the double-angle formula for cosine to write $\cos(6x)$ in terms of $\cos(3x)$. 

Solution

$$\begin{align*} \cos(6x)&= \cos(3x+3x)\\[4pt] &= \cos 3x \cos 3x-\sin 3x \sin 3x\\[4pt] &= {\cos}^2 3x-{\sin}^2 3x \end{align*}$$

Analysis

This example illustrates that we can use the double-angle formula without having exact values. It emphasizes that the pattern is what we need to remember and that identities are true for all values in the domain of the trigonometric function.

Use Double-Angle Formulas to Solve Equations

When solving equations,  fundamental identities are used to make solving equations simpler. Then basic rules of algebra are used to solve the equation.

Example $\PageIndex{3a}$: Use Double-Angle Formulas to Solve an Equation

Solve the equation exactly using a double-angle formula: $\cos(2\theta)=\cos \theta$.

Solution

We have three choices of expressions to substitute for the double-angle of cosine. As it is simpler to solve for one trigonometric function at a time, we will choose the double-angle identity involving only cosine:

$$\begin{align*} \cos(2\theta)&= \cos \theta\\ 2{\cos}^2 \theta-1&= \cos \theta\\ 2 {\cos}^2 \theta-\cos \theta-1&= 0\\ (2 \cos \theta+1)(\cos \theta-1)&= 0\\ 2 \cos \theta+1&= 0\\ \cos \theta&= -\dfrac{1}{2}\\ \cos \theta-1&= 0\\ \cos \theta&= 1 \end{align*}$$

So, if $\cos \theta=−\dfrac{1}{2}$,then $\theta=\dfrac{2\pi}{3}\pm 2\pi k$ and $\theta=\dfrac{4\pi}{3}\pm 2\pi k$; if $\cos \theta=1$,then $\theta=0\pm 2\pi k$.

Example $\PageIndex{3b}$ 

Solve the equation exactly using an identity: $3 \cos \theta+3=2 {\sin}^2 \theta$, $0≤\theta<2\pi$.

Solution

If we rewrite the right side, we can write the equation in terms of cosine:

$$\begin{align*} 3 \cos \theta+3&= 2 {\sin}^2 \theta\\ 3 \cos \theta+3&= 2(1-{\cos}^2 \theta)\\ 3 \cos \theta+3&= 2-2{\cos}^2 \theta\\ 2 {\cos}^2 \theta+3 \cos \theta+1&= 0\\ (2 \cos \theta+1)(\cos \theta+1)&= 0\\ 2 \cos \theta+1&= 0\\ \cos \theta&= -\dfrac{1}{2}\\ \theta&= \dfrac{2\pi}{3},\space \dfrac{4\pi}{3}\\ \cos \theta+1&= 0\\ \cos \theta&= -1\\ \theta&= \pi\\ \end{align*}$$

Our solutions are $\theta=\dfrac{2\pi}{3},\space \dfrac{4\pi}{3},\space \pi$.

Use Double-Angle Formulas to Verify Identities

The techniques used for solving equations are not the same as those for verifying identities. To verify an identity, one side of the identity  is rewritten to match the other side. 

Simplify

A first step in verifying identities or solving equations is recognizing patterns.

Example $\PageIndex{4}$ Simplify by Recognizing Identities

Simplify the expressions

a) $2\cos ^{2} \left(12{}^\circ \right)-1$

b) $8\sin \left(3x\right)\cos \left(3x\right)$

Solution

a) Notice that the expression is in the same form as one version of the double angle identity for cosine: $\cos (2\theta )=2\cos ^{2} (\theta )-1$. Using this,

$$2\cos ^{2} \left(12{}^\circ \right)-1=\cos \left(2\cdot 12{}^\circ \right)=\cos \left(24{}^\circ \right)\nonumber$$

b) This expression looks similar to the result of the double angle identity for sine.

$$\begin{array}{cl}8\sin \left(3x\right)\cos \left(3x\right) &\text{Factor a 4 out of the original expression}\\ 4\cdot 2\sin \left(3x\right)\cos \left(3x\right)  &\text{Applying the double angle identity}\\ 4\sin (6x) \end{array}\nonumber$$

 Try It $\PageIndex{4}$: Recognize and simplify

Use an identity to find the exact value of $\cos ^{2} \left(75{}^\circ \right)-\sin ^{2} \left(75{}^\circ \right)$.

Answer

$$\cos ^{2} \left(75{}^\circ \right)-\sin ^{2} \left(75{}^\circ \right)=\cos (2\cdot 75{}^\circ )  = \cos (150{}^\circ )=\dfrac{-\sqrt{3} }{2}\nonumber$$

Double angle formulas can be used to simplify expressions.

Example $\PageIndex{5}$: Simplify

Simplify $\dfrac{\cos (2t)}{\cos (t)-\sin (t)}$.

Solution

With three choices for how to rewrite the double angle, we need to consider which will be the most useful. To simplify this expression, it would be great if the denominator would cancel with something in the numerator, which would require a factor of $\cos (t)-\sin (t)$ in the numerator, which is most likely to occur if we rewrite the numerator with a mix of sine and cosine.

$$\begin{array}{cl} \dfrac{\cos (2t)}{\cos (t)-\sin (t)}     &\text{Apply the double angle identity}\\ =\dfrac{\cos ^{2} (t)-\sin ^{2} (t)}{\cos (t)-\sin (t)}     &\text{Factor the numerator}\\ =\dfrac{\left(\cos (t)-\sin (t)\right)\left(\cos (t)+\sin (t)\right)}{\cos (t)-\sin (t)}     &\text{Cancel the common factor}\\ \cos (t)+\sin (t)\nonumber      &\text{Result is in the most simplified form} \end{array} \nonumber$$

Verify

Establishing identities using the double-angle formulas is performed using the same steps as have been used previously to verify identities. Choose the more complicated side of the equation and rewrite it until it matches the other side.

Example $\PageIndex{6}$: Use Double-Angle Formulas to Verify an Identity

Verify the following identity using double-angle formulas:

$$1+\sin(2\theta)={(\sin\theta+\cos\theta)}^2 \nonumber$$

Solution

We will work on the right side of the equal sign and rewrite the expression until it matches the left side.

$\begin{array}{r|l} {(\sin \theta+\cos \theta)}^2&= {\sin}^2 \theta+2 \sin \theta \cos \theta+{\cos}^2 \theta\\[4pt] &= ({\sin}^2 \theta+{\cos}^2 \theta)+2 \sin \theta \cos \theta\\[4pt] &= 1+2 \sin \theta \cos \theta\\[4pt] &= 1+\sin(2\theta) \end{array}$

Analysis

This process is not complicated, as long as we recall the perfect square formula from algebra: ${(a\pm b)}^2=a^2\pm 2ab+b^2$, where here, $a=\sin \theta$ and $b=\cos \theta$. Part of being successful in mathematics is the ability to recognize patterns. While the terms or symbols may change, the algebra remains consistent.

 Try It $\PageIndex{6}$

Verify the identity: ${\cos}^4 \theta−{\sin}^4 \theta=\cos(2\theta)$. 

Answer

${\cos}^4 \theta−{\sin}^4 \theta=({\cos}^2 \theta+{\sin}^2 \theta)({\cos}^2 \theta−{\sin}^2 \theta)=\cos(2\theta)$

Example $\PageIndex{7}$ 

Verify the identity: $\tan(2 \theta)=2\cot \theta−\tan \theta$

Solution

In this case, we will work with the left side of the equation and simplify or rewrite until it equals the right side of the equation.

$$\begin{array}{r|ll} \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} & \text{Double-angle formula}\\[4pt] &= \dfrac{2 \tan \theta\left (\dfrac{1}{\tan \theta}\right)}{(1-{\tan}^2 \theta)\left (\dfrac{1}{\tan \theta}\right )} & \text{Multiply by a term that results in desired numerator}\\[4pt] &= \dfrac{2}{\dfrac{1}{\tan \theta}-\dfrac{ {\tan}^2 \theta}{\tan \theta}}\\[4pt] &= \dfrac{2}{\cot \theta-\tan \theta} & \text {Use reciprocal identity for } \dfrac{1}{\tan \theta} \end{array}$$

Analysis

Here is a case where the more complicated side of the initial equation appeared on the right, but we chose to work the left side. However, if we had chosen the left side to rewrite, we would have been working backwards to arrive at the equivalency. For example, suppose that we wanted to show

$$\begin{array}{r|ll} \dfrac{2\tan \theta}{1-{\tan}^2 \theta}&= \dfrac{2}{\cot \theta-\tan \theta} \\[4pt] &= \frac{2}{\dfrac{1}{\tan \theta }-\tan \theta }\left ( \dfrac{\tan \theta }{\tan \theta } \right ) & \text{Multiply by a term that results in desired numerator}\\[4pt] &= \dfrac{2 \tan \theta}{\dfrac{1}{\tan \theta}(\tan \theta)-\tan \theta(\tan \theta)}\\[4pt] &= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} \end{array}$$

When using the identities to simplify a trigonometric expression or solve a trigonometric equation, there are usually several paths to a desired result. There is no set rule as to what side should be manipulated. However, we should begin with the guidelines set forth earlier.

 Try It $\PageIndex{7}$

Verify the identity: $\cos(2\theta)\cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta$. 

Answer

$\cos(2 \theta)\cos \theta=({\cos}^2 \theta−{\sin}^2 \theta) \cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta$

Example $\PageIndex{8}$ 

Prove $\sec (2\alpha )=\dfrac{\sec ^{2} (\alpha )}{2-\sec ^{2} (\alpha )}$.

Solution

Since the right side seems a bit more complicated than the left side, we begin there.

$$\begin{array} {r|ll} \sec (2\alpha )   &= \dfrac{\sec ^{2} (\alpha )}{2-\sec ^{2} (\alpha )}   &\text{Rewrite the secants in terms of cosine} \\   &=  \dfrac{   \dfrac{1}{\cos^2 \alpha}}{ 2-\dfrac{1}{\cos^2 \alpha} }   &\text{Simplify complex fraction\(^{*}\) by multiplying by a convenient 1} \\    &=\dfrac{\dfrac{1}{\cos ^{2} (\alpha )} }{\left(2-\dfrac{1}{\cos ^{2} (\alpha )} \right)}  \cdot \dfrac{ \cos ^{2} (\alpha )}{ \cos ^{2} (\alpha )}  &\text{Multiply numerator; multiply denominator}\\  &=\dfrac{\dfrac{\cos ^{2} (\alpha )}{\cos ^{2} (\alpha )} }{2\cos ^{2} (\alpha )-\dfrac{\cos ^{2} (\alpha )}{\cos ^{2} (\alpha )} \cdot }  &\text{Simplify}\\     &=\dfrac{1}{2\cos ^{2} (\alpha )-1}  &\text{Rewrite the denominator as a double angle}\\   &=\dfrac{1}{\cos (2\alpha )}  &\text{Rewrite as a secant}\\ &=\sec (2\alpha )  &\text{Identity is verified} \nonumber \end{array}$$

$^{*}$At this point, we could have rewritten the bottom with common denominators, subtracted the terms, inverted and multiplied, then simplified. Instead, we chose to clear the fractions in numerator and denominator by multiplying both the top and bottom by $\cos ^{2} (\alpha )$, the common denominator.

Power Reduction Formulas 

The double-angle formulas can be used to derive the reduction formulas, which are formulas we can use to reduce the power of a given expression involving even powers of sine or cosine. They allow us to rewrite the even powers of sine or cosine in terms of the first power of cosine. These formulas are especially important in higher-level math courses, calculus in particular. Also called the power-reducing formulas, three identities are included and are easily derived from the double-angle formulas.

We can use two of the three double-angle formulas for cosine to derive the reduction formulas for sine and cosine. Let’s begin with $\cos(2\theta)=1−2 {\sin}^2 \theta$. Solve for ${\sin}^2 \theta$:

$$\begin{align*} \cos(2\theta)&= 1 -  2 {\sin}^2 \theta  \\[4pt]  2 {\sin}^2 \theta &=1-\cos(2\theta) \\[4pt] {\sin}^2 \theta &= \dfrac{1-\cos(2\theta)}{2} \end{align*}$$

Next, we use the formula $\cos(2\theta)=2 {\cos}^2 \theta−1$. Solve for ${\cos}^2 \theta$:

$$\begin{align*} \cos(2\theta)&= 2 {\cos}^2 \theta-1\\[4pt] 1+\cos(2\theta)&= 2 {\cos}^2 \theta\\[4pt] \dfrac{1+\cos(2\theta)}{2}&= {\cos}^2 \theta \end{align*}$$

The last reduction formula is derived by writing tangent in terms of sine and cosine:

$$\begin{align*} \tan^2 \theta &= \frac{\sin^2 \theta}{\cos^2 \theta} \\[4pt] &= \dfrac{\dfrac{1-\cos(2\theta)}{2}}{\dfrac{1+\cos(2\theta)}{2}} && \text{Substitute the reduction formulas} \\[4pt] &= \left(\dfrac{1-\cos(2 \theta)}{2}\right)\left(\dfrac{2}{1+\cos(2 \theta)}\right) \\[4pt] &= \dfrac{1-\cos(2 \theta)}{1+\cos(2 \theta)} \end{align*}$$

POWER REDUCTION FORMULAS

$${\sin}^2 \theta=\dfrac{1−\cos(2 \theta)}{2}$$

$${\cos}^2 \theta=\dfrac{1+\cos(2 \theta)}{2}$$

$${\tan}^2 \theta=\dfrac{1−\cos(2 \theta)}{1+\cos(2 \theta)}$$

Example $\PageIndex{9}$: Use Power Reduction Formulas

Write an equivalent expression for ${\cos}^4 x$ that does not involve any powers of sine or cosine greater than $1$.

Solution

We will apply the reduction formula for cosine twice.

$$\begin{align*} {\cos}^4 x&= {({\cos}^2 x)}^2\\[4pt] &= {\left(\dfrac{1+\cos(2x)}{2}\right)}^2\qquad \text{Substitute reduction formula}\\[4pt] &= \dfrac{1}{4}(1+2\cos(2x)+{\cos}^2 (2x))\\[4pt] &= \dfrac{1}{4}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{4}\left (\dfrac{1+{\cos}^2(2x)}{2}\right )\qquad \text{ Substitute reduction formula for } {\cos}^2 x\\[4pt] &= \dfrac{1}{4}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{8}+\dfrac{1}{8} \cos(4x)\\[4pt] &= \dfrac{3}{8}+\dfrac{1}{2} \cos(2x)+\dfrac{1}{8} \cos(4x) \end{align*}$$

Analysis

The solution is found by using the reduction formula twice, as noted, and the perfect square formula from algebra.

Example $\PageIndex{10}$: Use Power-Reducing Formulas to Prove an Identity

Use the power-reducing formulas to prove ${\sin}^3(2x)=\left[ \dfrac{1}{2} \sin(2x) \right] [ 1−\cos(4x)]$

Solution

We will work on simplifying the left side of the equation:

$$\begin{align*} {\sin}^3(2x)&= [\sin(2x)][{\sin}^2(2x)]\\[4pt] &= \sin(2x)\left [\dfrac{1-\cos(4x)}{2}\right ]\qquad \text{Substitute the power-reduction formula.}\\[4pt] &= \sin(2x)\left(\dfrac{1}{2}\right)[1-\cos(4x)]\\[4pt] &= \dfrac{1}{2}[\sin(2x)][1-\cos(4x)] \end{align*}$$

Analysis

Note that in this example, we substituted $\dfrac{1−\cos(4x)}{2}$ for ${\sin}^2(2x)$. The formula states ${\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}$. We let $\theta=2x$, so $2\theta=4x$.

 Try It $\PageIndex{11}$

Use the power-reducing formulas to prove that $10{\cos}^4 x=\dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x)$. 

Answer

$$\begin{align*} 10{\cos}^4 x&= 10{({\cos}^2x)}^2\\[4pt] &= 10{\left[\dfrac{ 1+\cos(2x)}{2} \right]}^2\qquad \text{Substitute reduction formula for } {\cos}^2x\\[4pt] &= \dfrac{10}{4}[1+2\cos(2x)+{\cos}^2(2x)]\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2}\cos(2x)+\dfrac{10}{4}\left(\dfrac{1+{\cos}^2(2x)}{2}\right)\qquad \text{ Substitute reduction formula for } {\cos}^2 x\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}$$

Half-Angle Formulas 

The next set of identities is the set of half-angle formulas, which can be derived from the reduction formulas and we can use when we have an angle that is half the size of a special angle. If we replace $\theta$ with $\dfrac{\alpha}{2}$, the half-angle formula for sine is found by simplifying the equation and solving for $\sin\left(\dfrac{\alpha}{2}\right)$. Note that the half-angle formulas are preceded by a $\pm$ sign. This does not mean that both the positive and negative expressions are valid. Rather, it depends on the quadrant in which $\dfrac{\alpha}{2}$ terminates.

The half-angle formula for sine is derived as follows:

$$\begin{align*} {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2}\\[4pt] {\sin}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\left(\cos 2\cdot \dfrac{\alpha}{2}\right)}{2} = \dfrac{1-\cos \alpha}{2}\\[4pt] \sin \left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}} \end{align*}$$

To derive the half-angle formula for cosine, we have

$$\begin{align*} {\cos}^2 \theta&= \dfrac{1+\cos(2\theta)}{2}\\[4pt] {\cos}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{2} = \dfrac{1+\cos \alpha}{2}\\[4pt] \cos\left(\dfrac{\pi}{2}\right)&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}} \end{align*}$$

For the tangent identity, we have

$$\begin{align*} {\tan}^2 \theta&= \dfrac{1-\cos(2\theta)}{1+\cos(2\theta)}\\[4pt] {\tan}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}\\[4pt] \tan\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} \end{align*}$$

HALF-ANGLE FORMULAS

$$\begin{align} \sin\left(\dfrac{\alpha}{2}\right)&=\pm \sqrt{\dfrac{1-\cos \alpha}{2}} \label{halfsine} \\[4pt] \cos \left(\dfrac{\alpha}{2} \right) &=\pm \sqrt{\dfrac{1+\cos \alpha}{2}} \\[4pt] \tan\left(\dfrac{\alpha}{2}\right) &=\pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} =\dfrac{\sin \alpha}{1+\cos \alpha} =\dfrac{1-\cos \alpha}{\sin \alpha}\end{align}$$

Example $\PageIndex{12}$: Use Half Angle Formulas to Evaluate a Trigonometric Expression

Using a Half-Angle Formula to Find the Exact Value of a Sine Function. Find $\sin(15°)$ using a half-angle formula.

Solution

Since $15°=\dfrac{30°}{2}$,we use the half-angle formula for sine (Equation $\ref{halfsine}$):

$$\begin{align*} \sin 15° = \sin \dfrac{30^{\circ}}{2}&= \sqrt{\dfrac{1-\cos 30^{\circ}}{2}}\\[4pt] &= \sqrt{\dfrac{1-\dfrac{\sqrt{3}}{2}}{2}}   = \sqrt{\dfrac{\dfrac{2-\sqrt{3}}{2}}{2}}   = \sqrt{\dfrac{2-\sqrt{3}}{4}}   = \dfrac{\sqrt{2-\sqrt{3}}}{2} \end{align*}$$

Remember that we can check the answer with a graphing calculator.

Analysis

Notice that we used only the positive root because $\sin(15°)$ is positive. 

Example $\PageIndex{13}$ 

Given that $\tan \alpha=\dfrac{8}{15}$ and $α$ lies in quadrant III, find the exact value of the following:

a.  $\sin\left(\dfrac{\alpha}{2}\right)$ $\qquad$ b. $\cos\left(\dfrac{\alpha}{2}\right)$$\qquad$ c. $\tan\left(\dfrac{\alpha}{2}\right)$

Solution

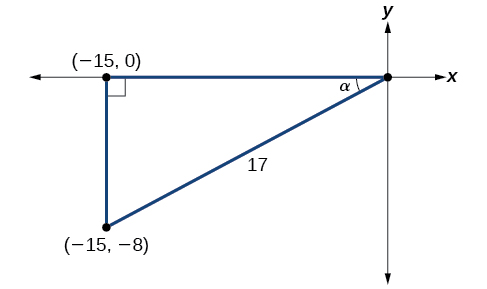Using the given information, we can draw the triangle shown to the right. Using the Pythagorean Theorem, we find the hypotenuse to be 17. Therefore, we can calculate $\sin \alpha=−\dfrac{8}{17}$ and $\cos \alpha=−\dfrac{15}{17}$. in summary then,  ${ \begin{matrix} \boxed { \begin{array}{llr}\cos \theta &=& -\dfrac{15}{17}\\  \sin \theta &=& -\dfrac{8}{17}\\ \tan \theta &=& \dfrac{8}{15} \end{array} } \end{matrix} }$.

Before we start, we must remember that if $α$ is in quadrant III, then $180°<\alpha<270°$,so $\dfrac{180°}{2}<\dfrac{\alpha}{2}<\dfrac{270°}{2}$. This means that the terminal side of $\dfrac{\alpha}{2}$ is in quadrant II, since $90°<\dfrac{\alpha}{2}<135°$.

1. To find $\sin \dfrac{\alpha}{2}$, we begin by writing the half-angle formula for sine. Then we substitute the value of the cosine we found from the triangle above and simplify. $$\begin{align*} \sin \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1-(-\dfrac{15}{17})}{2}} = \pm \sqrt{\dfrac{\dfrac{32}{17}}{ \; 2 \; }}  = \pm \sqrt{\dfrac{32}{17}\cdot \dfrac{1}{2}}   = \pm \sqrt{\dfrac{16}{17}}   = \pm \dfrac{4}{\sqrt{17}}   = \dfrac{4\sqrt{17}}{17} \end{align*}$$ We choose the positive value of $\sin \dfrac{\alpha}{2}$ because the angle $\dfrac{\alpha}{2}$ terminates in quadrant II and sine is positive in quadrant II.
2. To find $\cos \dfrac{\alpha}{2}$, we will write the half-angle formula for cosine, substitute the value of the cosine we found from the triangle above, and simplify.
   $$\begin{align*} \cos \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1+\left(-\dfrac{15}{17}\right)}{2}} = \pm \sqrt{\dfrac{\dfrac{2}{17}}{2}}  = \pm \sqrt{\dfrac{2}{17}\cdot \dfrac{1}{2}}   = \pm \sqrt{\dfrac{1}{17}}   = -\dfrac{\sqrt{17}}{17} \end{align*}$$ We choose the negative value of $\cos \dfrac{\alpha}{ \; 2 \; }$ because the angle $\dfrac{\alpha}{2}$ is in quadrant II because cosine is negative in quadrant II.
3. To find $\tan \dfrac{\alpha}{2}$, we write the half-angle formula for tangent. Again, we substitute the value of the cosine we found from the triangle above and simplify.
   $$\begin{align*} \tan \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}}\\[4pt] &= \pm \sqrt{\dfrac{1-\left(-\dfrac{15}{17}\right)}{1+\left(-\dfrac{15}{17}\right)}} = \pm \sqrt{\dfrac{\dfrac{32}{17}}{\; \dfrac{2}{17} \;}}   = \pm \sqrt{\dfrac{32}{2}}   = -\sqrt{16}   = -4 \end{align*}$$ We choose the negative value of $\tan \dfrac{\alpha}{2}$ because $\dfrac{\alpha}{2}$ lies in quadrant II, and tangent is negative in quadrant II.

 Try It $\PageIndex{14}$

Given that $\sin \alpha=−\dfrac{4}{5}$ and $\alpha$ lies in quadrant IV, find the exact value of $\cos \left(\dfrac{\alpha}{2}\right)$.​​​​​

Answer

$-\dfrac{2}{\sqrt{5}}$

Key Equations

Double-angle formulas
$\sin(2\theta)=2\sin \theta \cos \theta$	$\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta$ $=1−2{\sin}^2 \theta$ $=2{\cos}^2 \theta−1$	$\tan(2\theta)=\dfrac{2\tan \theta}{1−{\tan}^2 \theta}$
Reduction formulas
${\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}$	${\cos}^2 \theta=\dfrac{1+\cos(2\theta)}{2}$	${\tan}^2 \theta=\dfrac{1−\cos(2\theta)}{1+\cos(2\theta)}$
Half-angle formulas
$\sin \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{2}}$	$\cos \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}$	$\tan \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{1+\cos \alpha}}$ $=\dfrac{\sin \alpha}{1+\cos \alpha}$ $=\dfrac{1−\cos \alpha}{\sin \alpha}$

Key Concepts

• Double-angle identities are derived from the sum formulas of the fundamental trigonometric functions: sine, cosine, and tangent. 
• Reduction formulas are especially useful in calculus, as they allow us to reduce the power of the trigonometric term. 
• Half-angle formulas allow us to find the value of trigonometric functions involving half-angles, whether the original angle is known or not. 

Contributors and Attributions

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.