13.5E: The Chain Rule for Functions of Multiple Variables (Exercises)

Last updated
Save as PDF

Page ID: 10730

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

In exercises 1 - 6, use the information provided to solve the problem.

1) Let $ w(x,y,z)=xy\cos z,$ where $ x=t,y=t^2,$ and $ z=\arcsin t.$ Find $ \dfrac{dw}{dt}$.

Answer:: $ \dfrac{dw}{dt}=y\cos z+x\cos z(2t)−\dfrac{xy\sin z}{\sqrt{1−t^2}}$

2) Let $ w(t,v)=e^{tv}$ where $ t=r+s$ and $ v=rs$. Find $ \dfrac{∂w}{∂r}$ and $ \dfrac{∂w}{∂s}$.

3) If $ w=5x^2+2y^2, \quad x=−3u+v,$ and $ y=u−4v,$ find $ \dfrac{∂w}{∂u}$ and $ \dfrac{∂w}{∂v}$.

Answer:: $ \dfrac{∂w}{∂u}=−30x+4y \quad\ = \quad -30(-3u + v) + 4(u - 4v) \quad = \quad 90u -30v + 4u - 16v \quad = \quad 94u - 46v$,
$\dfrac{∂w}{∂v}=10x−16y \quad\ = \quad 10(-3u + v) - 16(u - 4v) \quad = \quad -30u +10v - 16u + 64v \quad = \quad -46u + 74v$

4) If $ w=xy^2,x=5\cos(2t),$ and $ y=5\sin(2t)$, find $ \dfrac{∂w}{∂t}$.

5) If $ f(x,y)=xy,x=r\cos θ,$ and $ y=r\sin θ$, find $\dfrac{∂f}{∂r}$ and express the answer in terms of $ r$ and $ θ$.

Answer:: $ \dfrac{∂f}{∂r}=r\sin(2θ)$

6) Suppose $ f(x,y)=x+y,u=e^x\sin y,\quad x=t^2$ and $ y=πt$, where $ x=r\cos θ$ and $ y=r\sin θ$. Find $ \dfrac{∂f}{∂θ}$.

In exercises 7 - 12, find $ \dfrac{dz}{dt}$ in two ways, first using the chain rule and then by direct substitution.

7) $ z=x^2+y^2, \quad x=t,y=t^2$

Answer:: $ \dfrac{dz}{dt}=2t+4t^3$

8) $ z=\sqrt{x^2+y^2},\quad y=t^2,x=t$

9) $ z=xy,\quad x=1−\sqrt{t},y=1+\sqrt{t}$

Answer:: $ \dfrac{dz}{dt}=−1$

10) $ z=\frac{x}{y},\quad x=e^t,y=2e^t$

11) $ z=\ln(x+y), \quad x=e^t,y=e^t$

Answer:: $ \dfrac{dz}{dt}=1$

12) $ z=x^4,\quad x=t,y=t$

13) Let $ w(x,y,z)=x^2+y^2+z^2, \quad x=cost,y=sint,$ and $ z=e^t$. Express $ w$ as a function of $ t$ and find $ \dfrac{dw}{dt}$ directly. Then, find $ \dfrac{dw}{dt}$ using the chain rule.

Answer:: $ \dfrac{dw}{dt}=2e^{2t}$ in both cases

14) Let $ z=x^2y,$ where $ x=t^2$ and $ y=t^3$. Find $ \dfrac{dz}{dt}$.

15) Let $ u=e^x\sin y,$ where $ x=-\ln 2t$ and $ y=πt$. Find $ \dfrac{du}{dt}$ when $ x=\ln 2$ and $ y=\frac{π}{4}$.

Answer:: $ \dfrac{du}{dt} = \sqrt{2}\big(\pi - 4\big)$

In exercises 16 - 33, find $ \dfrac{dy}{dx}$ using partial derivatives.

16) $ \sin(6x)+\tan(8y)+5=0$

17) $ x^3+y^2x−3=0$

Answer:: $ \dfrac{dy}{dx}=−\dfrac{3x^2+y^2}{2xy}$

18) $ \sin(x+y)+\cos(x−y)=4$

19) $ x^2−2xy+y^4=4$

Answer:: $ \dfrac{dy}{dx}=\dfrac{y−x}{−x+2y^3}$

20) $ xe^y+ye^x−2x^2y=0$

21) $ x^{2/3}+y^{2/3}=a^{2/3}$

Answer:: $ \dfrac{dy}{dx}=−\sqrt[3]{\frac{y}{x}}$

22) $ x\cos(xy)+y\cos x=2$

23) $ e^{xy}+ye^y=1$

Answer:: $ \dfrac{dy}{dx}=−\dfrac{ye^{xy}}{xe^{xy}+e^y(1+y)}$

24) $ x^2y^3+\cos y=0$

25) Find $ \dfrac{dz}{dt}$ using the chain rule where $ z=3x^2y^3,\,\,x=t^4,$ and $ y=t^2$.

Answer:: $ \dfrac{dz}{dt}=42t^{13}$

26) Let $ z=3\cos x−\sin(xy),x=\frac{1}{t},$ and $ y=3t.$ Find $ \dfrac{dz}{dt}$.

27) Let $ z=e^{1−xy},\,\, x=t^{1/3},$ and $ y=t^3$. Find $ \dfrac{dz}{dt}$.

Answer:: $ \dfrac{dz}{dt}=−\frac{10}{3}t^{7/3}×e^{1−t^{10/3}}$

28) Find $ \dfrac{dz}{dt}$ by the chain rule where $ z=\cosh^2(xy),\,\,x=\frac{1}{2}t,$ and $ y=e^t$.

29) Let $ z=\dfrac{x}{y},\,\, x=2\cos u,$ and $ y=3\sin v.$ Find $ \dfrac{∂z}{∂u}$ and $ \dfrac{∂z}{∂v}$.

Answer:: $ \dfrac{∂z}{∂u}=\dfrac{−2\sin u}{3\sin v}$ and $ \dfrac{∂z}{∂v}=\dfrac{−2\cos u\cos v}{3\sin^2v}$

30) Let $ z=e^{x^2y}$, where $ x=\sqrt{uv}$ and $ y=\frac{1}{v}$. Find $ \dfrac{∂z}{∂u}$ and $ \dfrac{∂z}{∂v}$.

31) If $ z=xye^{x/y},\,\, x=r\cos θ,$ and $ y=r\sin θ$, find $ \dfrac{∂z}{∂r}$ and $ \dfrac{∂z}{∂θ}$ when $ r=2$ and $ θ=\frac{π}{6}$.

Answer:: $ \dfrac{∂z}{∂r}=\sqrt{3}e^{\sqrt{3}}, \dfrac{∂z}{∂θ}=(2−4\sqrt{3})e^{\sqrt{3}}$

32) Find $ \dfrac{∂w}{∂s}$ if $ w=4x+y^2+z^3,\,\,x=e^{rs^2},\,\,y=\ln(\frac{r+s}{t}),$ and $ z=rst^2$.

33) If $ w=\sin(xyz),\,\,x=1−3t,\,\,y=e^{1−t},$ and $ z=4t$, find $ \dfrac{∂w}{∂t}$.

Answer:: $ \dfrac{∂w}{∂t}=-3yz\cos(xyz)−xze^{1−t}\cos(xyz)+4xy\cos(xyz)$

In exercises 34 - 36, use this information: A function $ f(x,y)$ is said to be homogeneous of degree $ n$ if $ f(tx,ty)=t^nf(x,y)$. For all homogeneous functions of degree $ n$, the following equation is true: $ x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)$. Show that the given function is homogeneous and verify that $ x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)$.

34) $ f(x,y)=3x^2+y^2$

35) $ f(x,y)=\sqrt{x^2+y^2}$

Answer:: $ f(tx,ty)=\sqrt{t^2x^2+t^2y^2}=t^1f(x,y), \quad \dfrac{∂f}{∂y}=x\frac{1}{2}(x^2+y^2)^{−1/2}×2x+y\frac{1}{2}(x^2+y^2)^{−1/2}×2y=1f(x,y)$

36) $ f(x,y)=x^2y−2y^3$

37) The volume of a right circular cylinder is given by $ V(x,y)=πx^2y,$ where $ x$ is the radius of the cylinder and $ y$ is the cylinder height. Suppose $ x$ and $ y$ are functions of $ t$ given by $ x=\frac{1}{2}t$ and $ y=\frac{1}{3}t$ so that $ x$ and $ y$ are both increasing with time. How fast is the volume increasing when $ x=2$ and $ y=5$? Assume time is measured in seconds.

Answer:: $ \ddfrac{dV}{dt} = \frac{34π}{3}\,\text{units}^3/\text{s}$

38) The pressure $ P$ of a gas is related to the volume and temperature by the formula $ PV=kT$, where temperature is expressed in kelvins. Express the pressure of the gas as a function of both $ V$ and $ T$. Find $ \dfrac{dP}{dt}$ when $ k=1, \dfrac{dV}{dt}=2$ cm³/min, $ \dfrac{dT}{dt}=12$ K/min, $ V=20 cm^3$, and $ T=20°F$.

39) The radius of a right circular cone is increasing at $ 3$ cm/min whereas the height of the cone is decreasing at $ 2$ cm/min. Find the rate of change of the volume of the cone when the radius is $ 13$ cm and the height is $ 18$ cm.

Answer:: $ \dfrac{dV}{dt}=\frac{1066π}{3}\,\text{cm}^3/\text{min}$

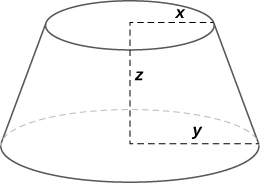
40) The volume of a frustum of a cone is given by the formula $ V=\frac{1}{3}πz(x^2+y^2+xy),$ where $ x$ is the radius of the smaller circle, $ y$ is the radius of the larger circle, and $ z$ is the height of the frustum (see figure). Find the rate of change of the volume of this frustum when $ x=10$ in., $y=12$ in., and $ z=18$ in.

$Frustum of a cone with height z, top radius of x and bottom radius of y.$

41) A closed box is in the shape of a rectangular solid with dimensions $ x,y,$ and $ z$. (Dimensions are in inches.) Suppose each dimension is changing at the rate of $ 0.5$ in./min. Find the rate of change of the total surface area of the box when $ x=2$ in., $y=3$ in., and $ z=1$ in.

Answer:: $ \dfrac{dA}{dt}=12\, \text{in.}^2/\text{min}$

42) The total resistance in a circuit that has three individual resistances represented by $ x,y,$ and $ z$ is given by the formula $ R(x,y,z)=\dfrac{xyz}{yz+xz+xy}$. Suppose at a given time the $ x$ resistance is $ 100\,Ω$, the $ y$ resistance is $ 200\,Ω,$ and the $ z$ resistance is $ 300\,Ω.$ Also, suppose the $ x$ resistance is changing at a rate of $ 2\,Ω/\text{min},$ the $ y$ resistance is changing at the rate of $ 1\,Ω/\text{min}$, and the $ z$ resistance has no change. Find the rate of change of the total resistance in this circuit at this time.

43) The temperature $ T$ at a point $ (x,y)$ is $ T(x,y)$ and is measured using the Celsius scale. A fly crawls so that its position after $ t$ seconds is given by $ x=\sqrt{1+t}$ and $ y=2+\frac{1}{3}t$, where $ x$ and $ y$ are measured in centimeters. The temperature function satisfies $ T_x(2,3)=4$ and $ T_y(2,3)=3$. How fast is the temperature increasing on the fly’s path after $ 3$ sec?

Answer:: $ 2$°C/sec

44) The $ x$ and $ y$ components of a fluid moving in two dimensions are given by the following functions: $ u(x,y)=2y$ and $ v(x,y)=−2x$ with $x≥0$ and $y≥0$. The speed of the fluid at the point $ (x,y)$ is $ s(x,y)=\sqrt{u(x,y)^2+v(x,y)^2}$. Find $ \dfrac{∂s}{∂x}$ and $ \dfrac{∂s}{∂y}$ using the chain rule.

45) Let $ u=u(x,y,z),$ where $ x=x(w,t),\, y=y(w,t),\, z=z(w,t),\, w=w(r,s)$, and $ t=t(r,s).$ Use a tree diagram and the chain rule to find an expression for $ \dfrac{∂u}{∂r}$.

Answer:: $ \frac{∂u}{∂r}=\frac{∂u}{∂x}(\frac{∂x}{∂w}\frac{∂w}{∂r}+\frac{∂x}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂y}(\frac{∂y}{∂w}\frac{∂w}{∂r}+\frac{∂y}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂z}(\frac{∂z}{∂w}\frac{∂w}{∂r}+\frac{∂z}{∂t}\frac{∂t}{∂r})$