Line Integrals (Exercises)

Last updated
Save as PDF

Page ID: 21160

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1. True or False? Line integral $\displaystyle\int _C f(x,y)\,ds$ is equal to a definite integral if $C$ is a smooth curve defined on $[a,b]$ and if function $f$ is continuous on some region that contains curve $C$.

Answer: True

2. True or False? Vector functions $\vecs r_1=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}, \quad 0≤t≤1,$ and $\vecs r_2=(1−t)\,\hat{\mathbf i}+(1−t)^2\,\hat{\mathbf j}, \quad 0≤t≤1$, define the same oriented curve.

3. True or False? $\displaystyle\int _{−C}(P\,dx+Q\,dy)=\int _C(P\,dx−Q\,dy)$

Answer: False

4. True or False? A piecewise smooth curve $C$ consists of a finite number of smooth curves that are joined together end to end.

5. True or False? If $C$ is given by $x(t)=t,\quad y(t)=t, \quad 0≤t≤1$, then $\displaystyle\int _Cxy\,ds=\int ^1_0t^2\,dt.$

Answer: False

For the following exercises, use a computer algebra system (CAS) to evaluate the line integrals over the indicated path.

6. [T] $\displaystyle\int _C(x+y)\,ds$

$C:x=t,y=(1−t),z=0$ from $(0, 1, 0)$ to $(1, 0, 0)$

7. [T] $\displaystyle \int _C(x−y)ds$

$C:\vecs r(t)=4t\,\hat{\mathbf i}+3t\,\hat{\mathbf j}$ when $0≤t≤2$

Answer: $\displaystyle\int _C(x−y)\,ds=10$

8. [T] $\displaystyle\int _C(x^2+y^2+z^2)\,ds$

$C:\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j}+8t\,\hat{\mathbf k}$ when $0≤t≤\dfrac{π}{2}$

9. [T] Evaluate $\displaystyle\int _Cxy^4\,ds$, where $C$ is the right half of circle $x^2+y^2=16$ and is traversed in the clockwise direction.

Answer: $\displaystyle\int _Cxy^4\,ds=\frac{8192}{5}$

10. [T] Evaluate $\displaystyle\int _C4x^3ds$, where C is the line segment from $(−2,−1)$ to $(1, 2)$.

For the following exercises, find the work done.

11. Find the work done by vector field $\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}$ on a particle moving along a line segment that goes from $(1,4,2)$ to $(0,5,1)$.

Answer: $W=8$ units of work

12. Find the work done by a person weighing 150 lb walking exactly one revolution up a circular, spiral staircase of radius 3 ft if the person rises 10 ft.

13. Find the work done by force field $\vecs F(x,y,z)=−\dfrac{1}{2}x\,\hat{\mathbf i}−\dfrac{1}{2}y\,\hat{\mathbf j}+\dfrac{1}{4}\,\hat{\mathbf k}$ on a particle as it moves along the helix $\vecs r(t)=\cos t\,\hat{\mathbf i}+\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k}$ from point $(1,0,0)$ to point $(−1,0,3π)$.

Answer: $W=\frac{3π}{4}$ units of work

14. Find the work done by vector field $\vecs{F}(x,y)=y\,\hat{\mathbf i}+2x\,\hat{\mathbf j}$ in moving an object along path $C$, which joins points $(1, 0)$ and $(0, 1)$.

15. Find the work done by force $\vecs{F}(x,y)=2y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}+(x+y)\,\hat{\mathbf k}$ in moving an object along curve $\vecs r(t)=\cos(t)\,\hat{\mathbf i}+\sin(t)\,\hat{\mathbf j}+16\,\hat{\mathbf k}$, where $0≤t≤2π$.

Answer: $W=π$ units of work

16. Find the mass of a wire in the shape of a circle of radius 2 centered at (3, 4) with linear mass density $ρ(x,y)=y^2$.

For the following exercises, evaluate the line integrals.

17. Evaluate $\displaystyle\int_C\vecs F·d\vecs{r}$, where $\vecs{F}(x,y)=−1\,\hat{\mathbf j}$, and $C$ is the part of the graph of $y=\frac{1}{2}x^3−x$ from $(2,2)$ to $(−2,−2)$.

Answer: $\displaystyle\int _C\vecs F·d\vecs{r}=4$ units of work

18. Evaluate $\displaystyle\int _γ(x^2+y^2+z^2)^{−1}ds$, where $γ$ is the helix $x=\cos t,y=\sin t,z=t,$ with $0≤t≤T.$

19. Evaluate $\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz$ over the line segment from $(1,1,1) $ to $(3,2,0).$

Answer: $\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz=−1$

20. Let $C$ be the line segment from point (0, 1, 1) to point (2, 2, 3). Evaluate line integral $\displaystyle\int _Cy\,ds.$

21. [T] Use a computer algebra system to evaluate the line integral $\displaystyle\int _Cy^2\,dx+x\,dy$, where $C$ is the arc of the parabola $x=4−y^2$ from $(−5, −3)$ to $(0, 2)$.

Answer: $\displaystyle\int _C(y^2)\,dx+(x)\,dy=\dfrac{245}{6}$

22. [T] Use a computer algebra system to evaluate the line integral $\displaystyle\int _C (x+3y^2)\,dy$ over the path $C$ given by $x=2t,y=10t,$ where $0≤t≤1.$

23. [T] Use a CAS to evaluate line integral $\displaystyle\int _C xy\,dx+y\,dy$ over path $C$ given by $x=2t,y=10t$, where $0≤t≤1$.

Answer: $\displaystyle\int _Cxy\,dx+y\,dy=\dfrac{190}{3}$

24. Evaluate line integral $\displaystyle\int _C(2x−y)\,dx+(x+3y)\,dy$, where $C$ lies along the $x$-axis from $x=0$ to $x=5$.

26. [T] Use a CAS to evaluate $\displaystyle\int _C\dfrac{y}{2x^2−y^2}\,ds$, where $C$ is defined by the parametric equations $x=t,y=t$, for $1≤t≤5.$

Answer: $\displaystyle\int _C\frac{y}{2x^2−y^2}\,ds=\sqrt{2}\ln 5$

27. [T] Use a CAS to evaluate $\displaystyle\int _Cxy\,ds$, where $C$ is defined by the parametric equations $x=t^2,y=4t$, for $0≤t≤1.$

In the following exercises, find the work done by force field $\vecs F$ on an object moving along the indicated path.

28. $\vecs{F}(x,y)=−x \,\hat{\mathbf i}−2y\,\hat{\mathbf j}$

$C:y=x^3$ from $(0, 0)$ to $(2, 8)$

Answer: $W=−66$ units of work

29. $\vecs{F}(x,y)=2x\,\hat{\mathbf i}+y\,\hat{\mathbf j}$

<$C$: counterclockwise around the triangle with vertices $(0, 0), (1, 0), $ and $(1, 1)$

30. $\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}−5z\,\hat{\mathbf k}$

$C:\vecs r(t)=2\cos t\,\hat{\mathbf i}+2\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k},\; 0≤t≤2π$

Answer: $W=−10π^2$ units of work

31. Let $\vecs F$ be vector field $\vecs{F}(x,y)=(y^2+2xe^y+1)\,\hat{\mathbf i}+(2xy+x^2e^y+2y)\,\hat{\mathbf j}$. Compute the work of integral $\displaystyle\int _C\vecs F·d\vecs{r}$, where $C$ is the path $\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j},\quad 0≤t≤\dfrac{π}{2}$.

32. Compute the work done by force $\vecs F(x,y,z)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}−z\,\hat{\mathbf k}$ along path $\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+t^3\,\hat{\mathbf k}$, where $0≤t≤1$.

Answer: $W=2$ units of work

33. Evaluate $\displaystyle\int _C\vecs F·d\vecs{r}$, where $\vecs{F}(x,y)=\dfrac{1}{x+y}\,\hat{\mathbf i}+\dfrac{1}{x+y}\,\hat{\mathbf j}$ and $C$ is the segment of the unit circle going counterclockwise from $(1,0)$ to $(0, 1)$.

34. Force $\vecs F(x,y,z)=zy\,\hat{\mathbf i}+x\,\hat{\mathbf j}+z^2x\,\hat{\mathbf k}$ acts on a particle that travels from the origin to point $(1, 2, 3)$. Calculate the work done if the particle travels:

along the path $(0,0,0)→(1,0,0)→(1,2,0)→(1,2,3)$ along straight-line segments joining each pair of endpoints;
along the straight line joining the initial and final points.
Is the work the same along the two paths?
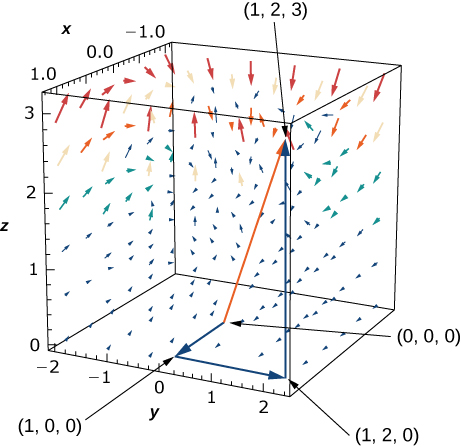
$clipboard_e7c787ff46860b19ec57c0669a08914af.png$

Answer: a. $W=11$ units of work;
b. $W=\dfrac{39}{4}=9\frac{3}{4}$ units of work;
c. No

35. Find the work done by vector field $\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}$ on a particle moving along a line segment that goes from $(1, 4, 2)$ to $(0, 5, 1).$

36. How much work is required to move an object in vector field $\vecs{F}(x,y)=y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}$ along the upper part of ellipse $\dfrac{x^2}{4}+y^2=1$ from $(2, 0)$ to $(−2,0)$?

Answer: $W=2π$ units of work

37. A vector field is given by $\vecs{F}(x,y)=(2x+3y)\,\hat{\mathbf i}+(3x+2y)\,\hat{\mathbf j}$. Evaluate the line integral of the field around a circle of unit radius traversed in a clockwise fashion.

38. Evaluate the line integral of scalar function $xy$ along parabolic path $y=x^2$ connecting the origin to point $(1, 1)$.

Answer: $\displaystyle\int _C f\,ds=\dfrac{25\sqrt{5}+1}{120}$

39. Find $\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy$ along $C: y=3x$ from $(0, 0)$ to $(1, 3).$

40. Find $\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy$ along $C: y^2=9x$ from $(0, 0)$ to $(1, 3).$

Answer: $\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy=6.15$

For the following exercises, use a CAS to evaluate the given line integrals.

41. [T] Evaluate $\vecs F(x,y,z)=x^2z\,\hat{\mathbf i}+6y\,\hat{\mathbf j}+yz^2\,\hat{\mathbf k}$, where $C$ is represented by $\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+\ln t \,\hat{\mathbf k},1≤t≤3$.

42. [T] Evaluate line integral $\displaystyle\int _γxe^y\,ds$ where, $γ$ is the arc of curve $x=e^y$ from $(1,0)$ to $(e,1)$.

Answer: $\displaystyle\int _γxe^y\,ds≈7.157$

43. [T] Evaluate the integral $\displaystyle\int _γxy^2\,ds$, where $γ$ is a triangle with vertices $(0, 1, 2), (1, 0, 3)$, and $(0,−1,0)$.

44. [T] Evaluate line integral $\displaystyle\int _γ(y^2−xy)\,dx$, where $γ$ is curve $y=\ln x$ from $(1, 0)$ toward $(e,1)$.

Answer: $\displaystyle\int _γ(y^2−xy)\,dx≈−1.379$

45. [T] Evaluate line integral $\displaystyle\int_γ xy^4\,ds$, where $γ$ is the right half of circle $x^2+y^2=16$.

46. [T] Evaluate $\int C \vecs F⋅d\vecs{r},\int C \vecs F·d\vecs{r},$ where $\vecs F(x,y,z)=x^2y\,\mathbf{\hat i}+(x−z)\,\mathbf{\hat j}+xyz\,\mathbf{\hat k}$ and

$C: \vecs r(t)=t\,\mathbf{\hat i}+t^2\,\mathbf{\hat j}+2\,\mathbf{\hat k},0≤t≤1$.

Answer: $\displaystyle\int _C \vecs F⋅d\vecs{r}≈−1.133$ units of work

47. Evaluate $\displaystyle\int _C \vecs F⋅d\vecs{r}$, where $\vecs{F}(x,y)=2x\sin y\,\mathbf{\hat i}+(x^2\cos y−3y^2)\,\mathbf{\hat j}$ and

$C$ is any path from $(−1,0)$ to $(5, 1)$.

48. Find the line integral of $\vecs F(x,y,z)=12x^2\,\mathbf{\hat i}−5xy\,\mathbf{\hat j}+xz\,\mathbf{\hat k}$ over path $C$ defined by $y=x^2, z=x^3$ from point $(0, 0, 0)$ to point $(2, 4, 8)$.

Answer: $\displaystyle\int _C \vecs F⋅d\vecs{r}≈22.857$ units of work

49. Find the line integral of $\displaystyle\int _C(1+x^2y)\,ds$, where $C$ is ellipse $\vecs r(t)=2\cos t\,\mathbf{\hat i}+3\sin t\,\mathbf{\hat j}$ from $0≤t≤π.$

For the following exercises, find the flux.

50. Compute the flux of $\vecs{F}=x^2\,\mathbf{\hat i}+y\,\mathbf{\hat j}$ across a line segment from $(0, 0)$ to $(1, 2).$

Answer: $\text{flux}=−\frac{1}{3}$

51. Let $\vecs{F}=5\,\mathbf{\hat i}$ and let $C$ be curve $y=0,$ with $0≤x≤4$. Find the flux across $C$.

52. Let $\vecs{F}=5\,\mathbf{\hat j}$ and let $C$ be curve $y=0,$ with $0≤x≤4$. Find the flux across $C$.

Answer: $\text{flux}=-20$

53. Let $\vecs{F}=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}$ and let $C: \vecs r(t)=\cos t\,\mathbf{\hat i}+\sin t\,\mathbf{\hat j}$ for $0≤t≤2π$. Calculate the flux across $C$.

54. Let $\vecs{F}=(x^2+y^3)\,\mathbf{\hat i}+(2xy)\,\mathbf{\hat j}$. Calculate flux $\vecs F$ orientated counterclockwise across the curve $C: x^2+y^2=9.$

Answer: $\text{flux}=0$

Complete the rest of the exercises as stated.

55. Find the line integral of $\displaystyle\int _C z^2\,dx+y\,dy+2y\,dz,$ where $C$ consists of two parts: $C_1$ and $C_2.$ $C_1$ is the intersection of cylinder $x^2+y^2=16$ and plane $z=3$ from $(0, 4, 3)$ to $(−4,0,3).$ $C_2$ is a line segment from $(−4,0,3)$ to $(0, 1, 5)$.

56. A spring is made of a thin wire twisted into the shape of a circular helix $x=2\cos t,\;y=2\sin t,\;z=t.$ Find the mass of two turns of the spring if the wire has a constant mass density of $ρ$ grams per cm.

Answer: $m=4πρ\sqrt{5}$ grams

57. A thin wire is bent into the shape of a semicircle of radius $a$. If the linear mass density at point $P$ is directly proportional to its distance from the line through the endpoints, find the mass of the wire.

58. An object moves in force field $\vecs F(x,y,z)=y^2\,\mathbf{\hat i}+2(x+1)y\,\mathbf{\hat j}$ counterclockwise from point $(2, 0)$ along elliptical path $x^2+4y^2=4$ to $(−2,0)$, and back to point $(2, 0)$ along the $x$-axis. How much work is done by the force field on the object?

Answer: $W=0$ units of work

59. Find the work done when an object moves in force field $\vecs F(x,y,z)=2x\,\mathbf{\hat i}−(x+z)\,\mathbf{\hat j}+(y−x)\,\mathbf{\hat k}$ along the path given by $\vecs r(t)=t^2\,\mathbf{\hat i}+(t^2−t)\,\mathbf{\hat j}+3\,\mathbf{\hat k}, \; 0≤t≤1.$

60. If an inverse force field $\vecs F$ is given by $\vecs F(x,y,z)=\dfrac{k}{‖r‖^3}r$, where $k$ is a constant, find the work done by $\vecs F$ as its point of application moves along the $x$-axis from $A(1,0,0)$ to $B(2,0,0)$.

Answer: $W=\frac{k}{2}$ units of work

61. David and Sandra plan to evaluate line integral $\displaystyle\int _C\vecs F·d\vecs{r}$ along a path in the $xy$-plane from $(0, 0)$ to $(1, 1)$. The force field is $\vecs{F}(x,y)=(x+2y)\,\mathbf{\hat i}+(−x+y^2)\,\mathbf{\hat j}$. David chooses the path that runs along the $x$-axis from $(0, 0)$ to $(1, 0)$ and then runs along the vertical line $x=1$ from $(1, 0)$ to the final point $(1, 1)$. Sandra chooses the direct path along the diagonal line $y=x$ from $(0, 0)$ to $(1, 1)$. Whose line integral is larger and by how much?

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.