4.7: Definite integrals by substitution.

Substitution for Definite Integrals

Substitution can be used with definite integrals, too. However, using substitution to evaluate a definite integral requires a change to the limits of integration. If we change variables in the integrand, the limits of integration change as well.

Substitution with Definite Integrals

Let \(u=g(x)\) and let \(g'\) be continuous over an interval \([a,b]\), and let \(f\) be continuous over the range of \(u=g(x).\) Then,

\[∫^b_af(g(x))g′(x)dx=∫^{g(b)}_{g(a)}f(u)\,du.\]

Although we will not formally prove this theorem, we justify it with some calculations here. From the substitution rule for indefinite integrals, if \(F(x)\) is an antiderivative of \(f(x),\) we have

\[ ∫f(g(x))g′(x)\,dx=F(g(x))+C.\]

Then

\[\begin{align} ∫^b_af[g(x)]g′(x)\,dx &= F(g(x))\bigg|^{x=b}_{x=a} \nonumber \\ &=F(g(b))−F(g(a)) \nonumber\\ &= F(u) \bigg|^{u=g(b)}_{u=g(a)} \nonumber\\ &=∫^{g(b)}_{g(a)}f(u)\,du \nonumber\end{align} \nonumber\]

and we have the desired result.

Example \(\PageIndex{5}\): Using Substitution to Evaluate a Definite Integral

Use substitution to evaluate \[ ∫^1_0x^2(1+2x^3)^5\,dx.\]

Solution

Let \(u=1+2x^3\), so \(du=6x^2dx\). Since the original function includes one factor of \(x^2\) and \(du=6x^2dx\), multiply both sides of the du equation by \(1/6.\) Then,

\[ du=6x^2\,dx\]

\[ \dfrac{1}{6}du=x^2\,dx.\]

To adjust the limits of integration, note that when \(x=0,u=1+2(0)=1,\) and when \(x=1,u=1+2(1)=3.\) Then

\[ ∫^1_0x^2(1+2x^3)^5dx=\dfrac{1}{6}∫^3_1u^5\,du.\]

Evaluating this expression, we get

\[ \dfrac{1}{6}∫^3_1u^5\,du=(\dfrac{1}{6})(\dfrac{u^6}{6})|^3_1=\dfrac{1}{36}[(3)^6−(1)^6]=\dfrac{182}{9}.\]

Exercise \(\PageIndex{5}\)

Use substitution to evaluate the definite integral \[ ∫^0_{−1}y(2y^2−3)^5\,dy.\]

Hint

Use the steps from Example to solve the problem.

Answer

\(\dfrac{91}{3}\)

Example \(\PageIndex{6}\): Using Substitution with an Exponential Function

Use substitution to evaluate \[ ∫^1_0xe^{4x^2+3}\,dx.\]

Solution

Let \(u=4x^3+3.\) Then, \(du=8x\,dx.\) To adjust the limits of integration, we note that when \(x=0,u=3\), and when \(x=1,u=7\). So our substitution gives

\[ ∫^1_0xe^{4x^2+3}\,dx=\dfrac{1}{8}∫^7_3e^udu=\dfrac{1}{8}e^u|^7_3=\dfrac{e^7−e^3}{8}≈134.568\]

Exercise \(\PageIndex{6}\)

Use substitution to evaluate \[ ∫^1_0x^2cos(\dfrac{π}{2}x^3)\,dx.\]

Hint

Use the process from Example to solve the problem.

Answer

\(\dfrac{2}{3π}≈0.2122\)

Substitution may be only one of the techniques needed to evaluate a definite integral. All of the properties and rules of integration apply independently, and trigonometric functions may need to be rewritten using a trigonometric identity before we can apply substitution. Also, we have the option of replacing the original expression for u after we find the antiderivative, which means that we do not have to change the limits of integration. These two approaches are shown in Example.

Example \(\PageIndex{7}\): Using Substitution to Evaluate a Trigonometric Integral

Use substitution to evaluate \[∫^{π/2}_0\cos^2θ\,dθ.\]

Solution

Let us first use a trigonometric identity to rewrite the integral. The trig identity \(\cos^2θ=\dfrac{1+\cos 2θ}{2}\) allows us to rewrite the integral as

\[∫^{π/2}_0\cos^2θdθ=∫^{π/2}_0\dfrac{1+\cos2θ}{2}\,dθ.\]

Then,

\[∫^{π/2}_0(\dfrac{1+\cos2θ}{2})dθ=∫^{π/2}_0(\dfrac{1}{2}+\dfrac{1}{2}\cos 2θ)\,dθ\]

\[=\dfrac{1}{2}∫^{π/2}_0\,dθ+∫^{π/2}_0\cos2θ\,dθ.\]

We can evaluate the first integral as it is, but we need to make a substitution to evaluate the second integral. Let \(u=2θ.\) Then, \(du=2\,dθ,\) or \(\dfrac{1}{2}\,du=dθ\). Also, when \(θ=0,u=0,\) and when \(θ=π/2,u=π.\) Expressing the second integral in terms of \(u\), we have

\(\dfrac{1}{2}∫^{π/2}_0\,dθ+\dfrac{1}{2}∫^{π/2}_0cos^2θ\,dθ=\dfrac{1}{2}∫^{π/2}_0\,dθ+\dfrac{1}{2}(\dfrac{1}{2})∫^π_0\cos u \,du\)

\(=\dfrac{θ}{2}|^{θ=π/2}_{θ=0}+\dfrac{1}{4}sinu|^{u=θ}_{u=0}\)

\(=(\dfrac{π}{4}−0)+(0−0)=\dfrac{π}{4}\)

Example \( \PageIndex{8}\): Evaluating a Definite Integral Using Inverse Trigonometric Functions

Evaluate the definite integral

\[ ∫^1_0\dfrac{dx}{\sqrt{1−x^2}}. \nonumber\]

Solution

We can go directly to the formula for the antiderivative in the rule on integration formulas resulting in inverse trigonometric functions, and then evaluate the definite integral. We have

\[ ∫^1_0\dfrac{dx}{\sqrt{1−x^2}}=\sin^{−1}x∣^1_0=\sin^{−1}1−\sin^{−1}0=\dfrac{π}{2}−0=\dfrac{π}{2}.\nonumber\

Example \( \PageIndex{9}\): Evaluating a Definite Integral

Evaluate the definite integral \( ∫^{\sqrt{3}}_{\sqrt{3}/3}\dfrac{dx}{1+x^2}\).

Solution

Use the formula for the inverse tangent. We have

\[ ∫^{\sqrt{3}}_{\sqrt{3}/3}\dfrac{dx}{1+x^2}=tan^{−1}x∣^{\sqrt{3}}_{\sqrt{3}/3} =[tan^{−1}(\sqrt{3})]−[tan^{−1}(\dfrac{\sqrt{3}}{3})]=\dfrac{π}{6}.\]

Exercise \(\PageIndex{9}\)

Evaluate the definite integral \( ∫^2_0\dfrac{dx}{4+x^2}\).

Hint

Follow the procedures from Example to solve the problem.

Answer

\[ \dfrac{π}{8}\]

As mentioned at the beginning of this section, exponential functions are used in many real-life applications. The number e is often associated with compounded or accelerating growth, as we have seen in earlier sections about the derivative. Although the derivative represents a rate of change or a growth rate, the integral represents the total change or the total growth. Let’s look at an example in which integration of an exponential function solves a common business application.

A price–demand function tells us the relationship between the quantity of a product demanded and the price of the product. In general, price decreases as quantity demanded increases. The marginal price–demand function is the derivative of the price–demand function and it tells us how fast the price changes at a given level of production. These functions are used in business to determine the price–elasticity of demand, and to help companies determine whether changing production levels would be profitable.

Example \(\PageIndex{4}\): Finding a Price–Demand Equation

Find the price–demand equation for a particular brand of toothpaste at a supermarket chain when the demand is 50 tubes per week at $2.35 per tube, given that the marginal price—demand function, \(p′(x),\) for x number of tubes per week, is given as

\[p'(x)=−0.015e^{−0.01x}.\]

If the supermarket chain sells 100 tubes per week, what price should it set?

Solution

To find the price–demand equation, integrate the marginal price–demand function. First find the antiderivative, then look at the particulars. Thus,

\[p(x)=∫−0.015e^{−0.01x}dx=−0.015∫e^{−0.01x}dx.\]

Using substitution, let \(u=−0.01x\) and \(du=−0.01dx\). Then, divide both sides of the du equation by −0.01. This gives

\[\dfrac{−0.015}{−0.01}∫e^udu=1.5∫e^udu=1.5e^u+C=1.5e^{−0.01}x+C.\]

The next step is to solve for C. We know that when the price is $2.35 per tube, the demand is 50 tubes per week. This means

\[p(50)=1.5e^{−0.01(50)}+C=2.35.\]

Now, just solve for C:

\[C=2.35−1.5e^{−0.5}=2.35−0.91=1.44.\]

Thus,

\[p(x)=1.5e^{−0.01x}+1.44.\]

If the supermarket sells 100 tubes of toothpaste per week, the price would be

\[p(100)=1.5e−0.01(100)+1.44=1.5e−1+1.44≈1.99.\]

The supermarket should charge $1.99 per tube if it is selling 100 tubes per week.

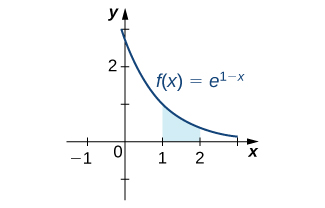
Example \(\PageIndex{5}\): Evaluating a Definite Integral Involving an Exponential Function

Evaluate the definite integral \[∫^2_1e^{1−x}dx.\]

Solution

Again, substitution is the method to use. Let \(u=1−x,\) so \(du=−1dx\) or \(−du=dx\). Then \(∫e^{1−x}dx=−∫e^udu.\) Next, change the limits of integration. Using the equation \(u=1−x\), we have

\[u=1−(1)=0\]

\[u=1−(2)=−1.\]

The integral then becomes

\[∫^2_1e^{1−x}\,dx=−∫^{−1}_0e^u\,du=∫^0_{−1}e^u\,du=eu|^0_{−1}=e^0−(e^{−1})=−e^{−1}+1.\]

See Figure.

Figure \(\PageIndex{2}\): The indicated area can be calculated by evaluating a definite integral using substitution.

Exercise \(\PageIndex{4}\)

Evaluate \(∫^2_0e^{2x}dx.\)

Hint

Let \(u=2x.\)

Answer

\(\dfrac{1}{2}∫^4_0e^udu=\dfrac{1}{2}(e^4−1)\)

Example \(\PageIndex{6}\): Growth of Bacteria in a Culture

Suppose the rate of growth of bacteria in a Petri dish is given by \(q(t)=3^t\), where t is given in hours and \(q(t)\) is given in thousands of bacteria per hour. If a culture starts with 10,000 bacteria, find a function \(Q(t)\) that gives the number of bacteria in the Petri dish at any time t. How many bacteria are in the dish after 2 hours?

Solution

We have

\[Q(t)=∫3^tdt=\dfrac{3^t}{\ln 3}+C.\]

Then, at \(t=0\) we have \(Q(0)=10=\dfrac{1}{\ln 3}+C,\) so \(C≈9.090\) and we get

\[Q(t)=\dfrac{3^t}{\ln 3}+9.090.\]

At time \(t=2\), we have

\[Q(2)=\dfrac{3^2}{\ln 3}+9.090\]

\[=17.282.\]

After 2 hours, there are 17,282 bacteria in the dish.

Exercise \(\PageIndex{5}\)

From Example, suppose the bacteria grow at a rate of \(q(t)=2^t\). Assume the culture still starts with 10,000 bacteria. Find \(Q(t)\). How many bacteria are in the dish after 3 hours?

Hint

Use the procedure from Example to solve the problem

Answer

\(Q(t)=\dfrac{2^t}{\ln 2}+8.557.\) There are 20,099 bacteria in the dish after 3 hours.

Example \(\PageIndex{7}\): Fruit Fly Population Growth

Suppose a population of fruit flies increases at a rate of \(g(t)=2e^{0.02t}\), in flies per day. If the initial population of fruit flies is 100 flies, how many flies are in the population after 10 days?

Solution

Let \(G(t)\) represent the number of flies in the population at time t. Applying the net change theorem, we have

\(G(10)=G(0)+∫^{10}_02e^{0.02t}dt\)

\(=100+[\dfrac{2}{0.02}e^{0.02t}]∣^{10}_0\)

\(=100+[100e^{0.02t}]∣^{10}_0\)

\(=100+100e^{0.2}−100\)

\(≈122.\)

There are 122 flies in the population after 10 days.

Exercise \(\PageIndex{6}\)

Suppose the rate of growth of the fly population is given by \(g(t)=e^{0.01t},\) and the initial fly population is 100 flies. How many flies are in the population after 15 days?

Hint

Use the process from Example to solve the problem.

Answer

There are 116 flies.

Example \(\PageIndex{8}\): Evaluating a Definite Integral Using Substitution

Evaluate the definite integral using substitution: \[∫^2_1\dfrac{e^{1/x}}{x^2}\,dx.\]

Solution

This problem requires some rewriting to simplify applying the properties. First, rewrite the exponent on e as a power of x, then bring the \(x^2\) in the denominator up to the numerator using a negative exponent. We have

\[∫^2_1\dfrac{e^{1/x}}{x^2}\,dx=∫^2_1e^{x^{−1}}x^{−2}\,dx.\]

Let \(u=x^{−1},\) the exponent on \(e\). Then

\[du=−x^{−2}\,dx\]

\[−du=x^{−2}\,dx.\]

Bringing the negative sign outside the integral sign, the problem now reads

\[−∫e^u\,du.\]

Next, change the limits of integration:

\[u=(1)^{−1}=1\]

\[u=(2)^{−1}=\dfrac{1}{2}.\]

Notice that now the limits begin with the larger number, meaning we must multiply by −1 and interchange the limits. Thus,

\[−∫^{1/2}_1e^udu=∫^1_{1/2}e^udu=e^u|^1_{1/2}=e−e^{1/2}=e−\sqrt{e}.\]

Exercise \(\PageIndex{7}\)

Evaluate the definite integral using substitution: \[∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}dx.\]

Hint

Let \(u=4x^{−2}.\)

Answer

\[∫^2_1\dfrac{1}{x^3}e^{4x^{−2}}dx=\dfrac{1}{8}[e^4−e]\].

Example is a definite integral of a trigonometric function. With trigonometric functions, we often have to apply a trigonometric property or an identity before we can move forward. Finding the right form of the integrand is usually the key to a smooth integration.

Example \(\PageIndex{12}\): Evaluating a Definite Integral

Find the definite integral of \[∫^{π/2}_0\dfrac{\sin x}{1+\cos x}dx.\]

Solution

We need substitution to evaluate this problem. Let \(u=1+\cos x\) so \(du=−\sin x\,dx.\) Rewrite the integral in terms of u, changing the limits of integration as well. Thus,

\[u=1+cos(0)=2\]

\[u=1+cos(\dfrac{π}{2})=1.\]

Then

\[∫^{π/2}_0\dfrac{\sin x}{1+\cos x}=−∫^1+2u^{−1}du=∫^2_1u^{−1}du=\ln |u|^2_1=[\ln 2−\ln 1]=\ln 2\]

Key Concepts

• Substitution is a technique that simplifies the integration of functions that are the result of a chain-rule derivative. The term ‘substitution’ refers to changing variables or substituting the variable u and du for appropriate expressions in the integrand.
• When using substitution for a definite integral, we also have to change the limits of integration.

Key Equations

• Substitution with Definite Integrals

\(∫^b_af(g(x))g'(x)dx=∫^{g(b)}_{g(a)}f(u)du\)

Glossary

change of variables

the substitution of a variable, such as u, for an expression in the integrand

integration by substitution

a technique for integration that allows integration of functions that are the result of a chain-rule derivative

Contributors and Attributions

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.