4.E: Basic Concepts of Euclidean Geometry (Exercises)

Exercise $\PageIndex{1}$: Similarity

Assess whether each of the following statement is true or false and justify your answer.

1. Any two equilateral triangles are similar.
2. Any two isosceles triangles are similar.
3. Any two squares are similar.
4. Any two rectangles are similar.
5. Any two pentagons are similar.
6. Any two polygons are similar.

Exercise $\PageIndex{2}$: Area

Starting with the formula for the area of a triangle, show how to obtain the formula for the area of a parallelogram and the area of a hexagon.

Exercise $\PageIndex{3}$: Interior angle

Find the general formula for the center angle in a regular n-sided polygon. Justify your answer.

Find the general formula for the exterior angle in a regular n-sided polygon. Justify your answer.

Exercise $\PageIndex{4}$: Triangles

Prove or disprove the following: an equilateral triangle is an isosceles triangle.

Explain why an equilateral triangle is not a scalene triangle.

Exercise $\PageIndex{5}$: True or False

Explain why the following statements below are true.

1. A square is a rectangle.
2. A rectangle is a parallelogram.
3. A square is a kite.
4. A parallelogram is a trapezoid.

Exercise $\PageIndex{6}$: Angles

Given cutout sheets with angles $40^{\circ}, 55^{\circ }$ and $85^{\circ}$. By adding or subtracting angles, construct other angles that measure $15^{\circ}, 30^{\circ}, 70^{\circ}, 95^{\circ}$and $100^{\circ}.$

Can you construct an angle that measures $75^{\circ}?$Explain how or say why not.

Exercise $\PageIndex{7}$: Converse of the Pythagorean Theorem

State the statement for the converse of the Pythagorean Theorem. Is this statement true or false? Justify your answer.

Exercise $\PageIndex{8}$: Venn diagram

Create a Venn diagram to illustrate the types of quadrilaterals listed in this section.

Exercise $\PageIndex{9}$: Parallelogram

Let $(a; b); ((0; c); (d:e); (f; 0)$ be vertices of a quadrilateral. Show that if you take the midpoints of any quadrilateral and connect them in turn, you will always get a parallelogram.

Exercise $\PageIndex{10}$: Venn Triangles

Express the relationship between scalene, isosceles and equilateral triangles with a Venn diagram.

Exercise $\PageIndex{11}$: Angles

Consider the figure:

Given that  \( a= 47^{\circ}, \) and \(c= 55^{\circ}.\)

Find other listed angles.

Exercise $\PageIndex{12}$:

 

Refer to the cube picture above.

Name the following:

1. Two line segments that do not lie in the same plane.
2. Two intersecting line segments.
3. Three concurrent line segments that do not lie in the same plane.
4. Two skew line segments.
5. A pair of supplementary angles.
6. A pair of perpendicular line segments.
7. Two parallel line segments.

Exercise $\PageIndex{13}$: Inner Circle

Find the area between the perimeter of this square and the unit circle.

Answer

$1- \pi$

Exercise $\PageIndex{14}$: Outer Circle

Find the area between the perimeter of the unit circle and the triangle created from connecting the points $(0,1), (−\frac{4}{5}, −\frac{3}{5})$and $\displaystyle (\frac{4}{5}, −\frac{3}{5})$, as seen in the following figure.

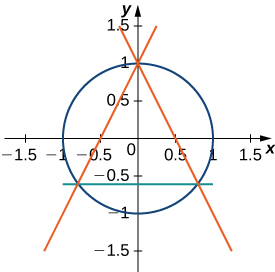
Answer

(\displaystyle π−\frac{32}{25}\)

Exercise $\PageIndex{15}$: Reuleaux triangle

The Reuleaux triangle consists of an equilateral triangle and three regions, each of them bounded by the side of the triangle and an arc of a circle of radius \(s \) centred at the opposite vertex of the triangle. Show that the area of the Reuleaux triangle in the following figure of side length $s$ is $\frac{s^2}{2}(\pi - \sqrt{3})$.

 

 

https://texample.net/tikz/examples/all/

Exercises 13-16 are from

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.