1.1E: Exercises

Last updated
Save as PDF

Page ID: 18539

This page is a draft and is under active development.

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The answers were provided to selected problems.

Exercise $\PageIndex{1}$

Derive the formula for the volume of a sphere using the slicing method.

Answer: $\dfrac{4}{3}\pi R^3$

Solution:

As in most problems we should choose to graph the function first. We know the formula for a circle, $x^2+y^2=r^2$ and solving for y we get $y=\pm\sqrt{R^2-x^2}$. When graphed they appear as:

$exercise1 slicing.png$

With the blue line being the positive values and the green the negatives. Now we must find what an area of a slice will be. As we are trying to find the volume of a sphere the area of a slice must be a circle, with radius $y=r=\sqrt{R^2-x^2}$.

Setting up the area of a slice we get \[A(x)=\pi r^2=\pi (\sqrt{R^2-x^2})^2=\pi(R^2-x^2)\]

Integrating over the interval of $[-R,R]$ we get: \[V=\pi \int_{-R}^{R}(R^2-x^2)dx=\pi \Big[R^2x-\dfrac{1}{3}x^3\Big]_{-R}^{R}=\dfrac{4}{3}\pi R^3\]

Exercise $\PageIndex{2}$

Derive the formula for the volume of a cone.

Answer: $\dfrac{\pi R^2h}{3}$

Solution:

Draw a picture, similar to:

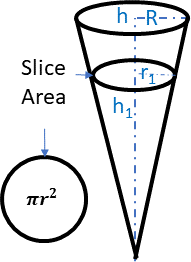
$E1.12_Cone.png$

Note the area of a slice is $ \pi r^2 $ and that the triangle formed by the origin, h₁ and r₁ is similar to the triangle formed by the origin, h and R. Thus $ r_1 = \dfrac{Rh_1}{h} $, with R and h being constants.

Integrating over the interval of $[0, R] $ we get: $ V= \pi \int_{0}^{R} \dfrac{R^2 y^2}{h^2}\, dy= \dfrac{\pi R^2 y^3}{3h^2}\Big|_0^h=\dfrac{\pi R^2h}{3} $. Note, had we drawn the cone on it's side, the variable of integration would have been $ x$ and we would have rotated around the $x$ axis.

Exercise $\PageIndex{3}$

Use the slicing method to derive the formula for the volume of a tetrahedron with side length a.

Answer

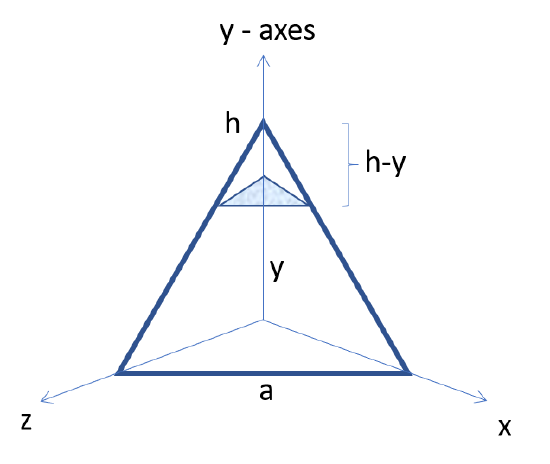
Draw a picture similar to the image below, with the height of the tetrahedron centered on one of the axes. We've chosen the y-axis. $1.1E3_Tetrahedron.png$

Note that the height of the regular tetrahedron is $ \dfrac{\sqrt{6}}{3} a $. To find this, you must first find the distance from one of the vertices to the center of the tetrahedron. Then use that base length with a side length of $ a$ to find the height.

Once the height is obtained. The area of a triangle slice at a particular height becomes $\dfrac{\sqrt{3}}{4}(a-\dfrac{\sqrt{3}y}{2})^2 $. Integrating from zero to $ \dfrac{\sqrt{6}}{3} a $, we obtain the volume of a regular tetrahedron is $ V = \dfrac{a^3 \sqrt{2}}{12} $.

Exercise $\PageIndex{4}$

Use the disk method to derive the formula for the volume of a trapezoidal cylinder.

Answer

First, start with a diagram.

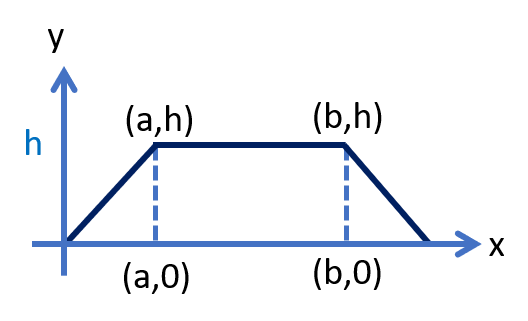
$1.1E4_Trapezoid.png$

Then construct the disks. From zero to a and b the area of our disk will be $ \pi r^2 $, where $r $ is the height of the triangle and given by $ r= \dfrac{hx}{a} $. Thus the volume rotated around the x axis would be $ \int_0^a \pi (\dfrac{hx}{a})^2\, dx = \dfrac{\pi ha^2}{3} $. Since the middle section has a constant radius of h, then $ V =\int_a^b \pi (h)^2\, dx = \pi h^2(b-a) $. The final piece would be determined similar to the first piece assuming $w-b=a$, then we obtain $V = \dfrac{2 \pi ha^2}{3}+\pi h^2(b-a) $.

Exercise $\PageIndex{5}$

Explain when you would use the disk method versus the washer method. When are they interchangeable?

Answer: The disk method is used when rotating a function that abuts the axis of rotation. The washer method is used when rotating a function that does not abut the chosen axis of rotation, thus forming a shape that looks like a washer in 2D or a doughnut in 3D. They are interchangeable when the function abuts the axis of rotation.

For exercises 6 - 10, draw a typical slice and find the volume using the slicing method for the given volume.

Exercise $\PageIndex{6}$

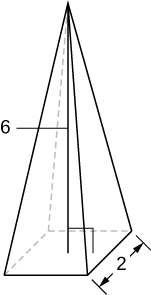
A pyramid with height 6 units and square base of side 2 units, as pictured here.

$alt$

Answer: Here the cross-sections are squares taken perpendicular to the $y$-axis.
We use the vertical cross-section of the pyramid through its center to obtain an equation relating $x$ and $y$.
Here this would be the equation, $ y = 6 - 6x $. Since we need the dimensions of the square at each $y$-level, we solve this equation for $x$ to get, $x = 1 - \tfrac{y}{6}$.
This is half the distance across the square cross-section at the $y$-level, so the side length of the square cross-section is, $s = 2\left(1 - \tfrac{y}{6}\right).$
Thus, we have the area of a cross-section is,

$A(y) = \left[2\left(1 - \tfrac{y}{6}\right)\right]^2 = 4\left(1 - \tfrac{y}{6}\right)^2.$

$\begin{align*} \text{Then},\quad V &= \int_0^6 4\left(1 - \tfrac{y}{6}\right)^2 \, dy \\[5pt]
&= -24 \int_1^0 u^2 \, du, \quad \text{where} \, u = 1 - \tfrac{y}{6}, \, \text{so} \, du = -\tfrac{1}{6}\,dy, \quad \implies \quad -6\,du = dy \\[5pt]
&= 24 \int_0^1 u^2 \, du = 24\dfrac{u^3}{3}\bigg|_0^1 \\[5pt]
&= 8u^3\bigg|_0^1 \\[5pt]
&= 8\left( 1^3 - 0^3 \right) \quad= \quad 8\, \text{units}^3 \end{align*}$

Exercise $\PageIndex{7}$

A pyramid with height 4 units and a rectangular base with length 2 units and width 3 units, as pictured here.

$alt$

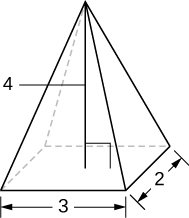
Answer: Here the cross-sections are rectangles taken perpendicular to the $y$-axis.
We use the vertical cross-section of the pyramid through its center to obtain an equation relating $x$ and $y$ and $ z $ and $ y$.
Here the equations are $ y = 4 - 4x $ and $ z=4-\dfrac{8x}{3} $. Since we need the dimensions of the rectangle at each $y$-level, we solve these equation for $x$ to get, $x = 1 - \tfrac{y}{4}$ for the side of length 2 and for $z$ to get, $z = \dfrac{3}{2}(1 - \tfrac{y}{4})$ for the side of length 3.
These are half the distance from the y axis, so the side lengths of the rectangular cross-section are: $s_2 = 2\left(1 - \tfrac{y}{4}\right).$ and $s_3 = 3\left(1 - \tfrac{y}{4}\right).$
Thus, we have the area of a cross-section is,

$A(y) = \left[2\left(1 - \tfrac{y}{4}\right)\right] \left[3\left(1 - \tfrac{y}{4}\right)\right] = 6\left(1 - \tfrac{y}{4}\right)^2.$

$\begin{align*} \text{Then},\quad V &= \int_0^4 6\left(1 - \tfrac{y}{4}\right)^2 \, dy \\[5pt]
&= -24 \int_1^0 u^2 \, du, \quad \text{where} \, u = 1 - \tfrac{y}{4}, \, \text{so} \, du = -\tfrac{1}{4}\,dy, \quad \implies \quad -4\,du = dy \\[5pt]
&= 24 \int_0^1 u^2 \, du = 24\dfrac{u^3}{3}\bigg|_0^1 \\[5pt]
&= 8u^3\bigg|_0^1 \\[5pt]
&= 8\left( 1^3 - 0^3 \right) \quad= \quad 8\, \text{units}^3 \end{align*}$

Exercise $\PageIndex{8}$

A tetrahedron with a base side of 4 units,as seen here.

$alt$

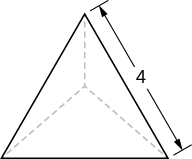
Answer: $V = \dfrac{32}{3\sqrt{2}} = \dfrac{16\sqrt{2}}{3}$ units³

Exercise $\PageIndex{9}$

A pyramid with height 5 units, and an isosceles triangular base with lengths of 6 units and 8 units, as seen here.

$alt$

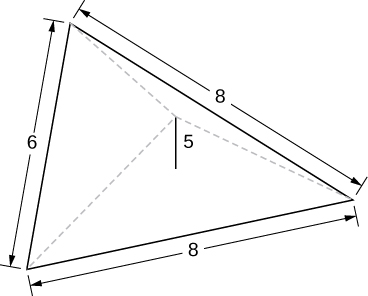
Answer

The area of an isosceles triangle using geometry is $ A=\dfrac{1}{2} s^2 \sin\theta $, where $s$ is the length of the isosceles sides and $\theta$ is the angle between them, which is 0.76879 radians (or approximately 44 degrees). Now we need to relate the height of the pyramid with the side length at that height. Solving for a linear equation with two points in terms of $ s$, we obtain $ s = \dfrac{8}{5}(5-y) $.

$ V = \int_0^5 \dfrac{1}{2} (\dfrac{8}{5}(5-y))^2 sin(0.76879) \, dy = 0.89 \int_0^5 (5-y)^2 \, dy = 0.89 \int_{u=0}^{u=5} u^2\, du = 47.46 \, \text{units}^3. $

Exercise $\PageIndex{10}$

A cone of radius $ r$ and height $ h$ has a smaller cone of radius $ r/2$ and height $ h/2$ removed from the top, as seen here. The resulting solid is called a frustum.

$alt$

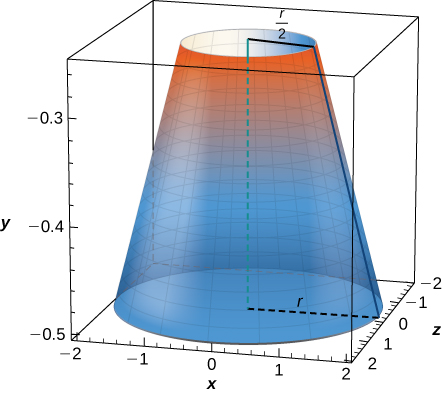
Answer: $V = \dfrac{7\pi}{12} hr^2$ units³

For exercises 11 - 16, draw an outline of the solid and find the volume using the slicing method.

Exercise $\PageIndex{11}$

The base is a circle of radius $ a$. The slices perpendicular to the base are squares.

Answer

$CircularBaseSquareCrossSection.png$

$ \int_{-a}^a 4(a^2-x^2)\, dx = \dfrac{16a^3}{3} \, \text{units}^3. $

Exercise $\PageIndex{12}$

The base is a triangle with vertices $ (0,0),(1,0),$ and $ (0,1)$. Slices perpendicular to the $xy$-plane are semicircles.

Answer

$alt$

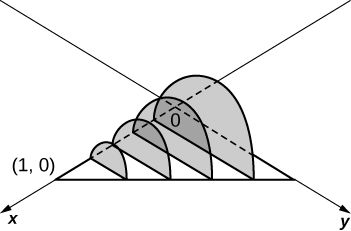
$\displaystyle V = \int_0^1 \dfrac{\pi(1-x)^2}{8}\, dx \quad = \quad \dfrac{π}{24}$ units³

Exercise $\PageIndex{13}$

The base is the region under the parabola $ y=1−x^2$ in the first quadrant. Slices perpendicular to the $xy$-plane are squares.

Answer: TBD

Exercise $\PageIndex{14}$

The base is the region under the parabola $ y=1−x^2$ and above the $x$-axis. Slices perpendicular to the $y$-axis are squares.

Answer

$alt$

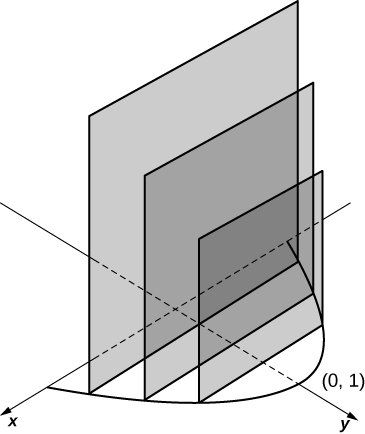
$\displaystyle V = \int_0^1 4(1 - y)\,dy \quad = \quad 2$ units³

Exercise $\PageIndex{15}$

The base is the region enclosed by $ y=x^2$ and $ y=9.$ Slices perpendicular to the $x$-axis are right isosceles triangles.

Answer: TBD

Exercise $\PageIndex{16}$

The base is the area between $ y=x$ and $ y=x^2$. Slices perpendicular to the $x$-axis are semicircles.

Answer

$alt$

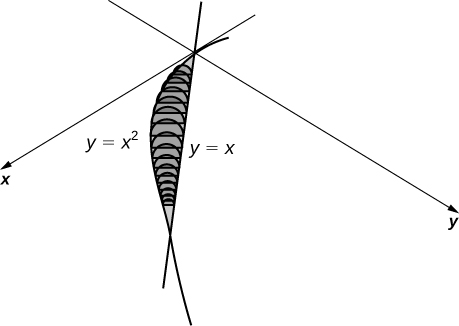
$\displaystyle V = \int_0^1 \dfrac{\pi}{8}\left( x - x^2 \right)^2 \, dx \quad=\quad \dfrac{π}{240}$ units³

Disk and Washer Method

For exercises 17 - 24, draw the region bounded by the curves. Then, use the disk or washer method to find the volume when the region is rotated around the $x$-axis.

Exercise $\PageIndex{17}$

$ x+y=8,\quad x=0$, and $ y=0$

Answer: TBD

Exercise $\PageIndex{18}$

$ y=2x^2,\quad x=0,\quad x=4,$ and $ y=0$

Answer

$alt$

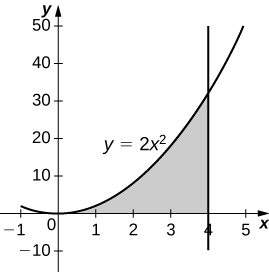
$\displaystyle V = \int_0^4 4\pi x^4\, dx \quad=\quad \dfrac{4096π}{5}$ units³

Exercise $\PageIndex{19}$

$ y=e^x+1,\quad x=0,\quad x=1,$ and $ y=0$

Answer: TBD

Exercise $\PageIndex{20}$

$ y=x^4,\quad x=0$, and $ y=1$

Answer

$alt$

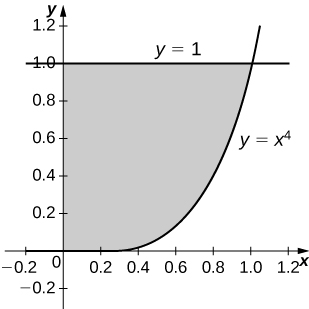
$\displaystyle V = \int_0^1 \pi\left( 1^2 - \left( x^4\right)^2\right)\, dx = \int_0^1 \pi\left( 1 - x^8\right)\, dx \quad = \quad \dfrac{8π}{9}$ units³

Exercise $\PageIndex{21}$

$y=\sqrt{x}, \, x=0, \, x=4$ and $y=0$

Answer: TBD

Exercise $\PageIndex{22}$

$ y=\sin(x), \, y=\cos(x)$ and $ x=0$

Answer

$alt$

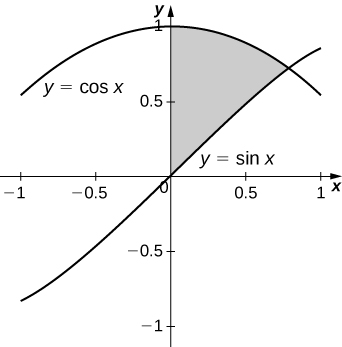
$\displaystyle V = \int_0^{\pi/4} \pi \left( \cos^2 x - \sin^2 x\right) \, dx = \int_0^{\pi/4} \pi \cos 2x \, dx \quad=\quad \dfrac{π}{2}$ units³

Exercise $\PageIndex{23}$

$y=\dfrac{1}{x}, \, x=2$, and $ y=3$

Answer: TBD

Exercise $\PageIndex{24}$

$ x^2−y^2=9$ and $ x+y=9,\quad y=0$ and $ x=0$

Answer

$alt$

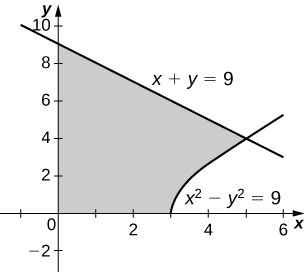
$V = 207π$ units³

For exercises 25 - 32, draw the region bounded by the curves. Then, find the volume when the region is rotated around the $y$-axis.

Exercise $\PageIndex{25}$

$ y=4−\dfrac{1}{2}x,\quad x=0,$ and $ y=0$

Answer: TBD

Exercise $\PageIndex{26}$

$ y=2x^3,\quad x=0,\quad x=1,$ and $ y=0$

Answer

$alt$

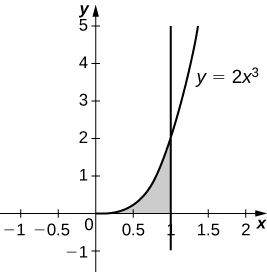
$V = \dfrac{4π}{5}$ units³

Exercise $\PageIndex{27}$

$ y=3x^2,\quad x=0,$ and $ y=3$

Answer: TBD

Exercise $\PageIndex{28}$

$y=\sqrt{4-x^2},\, y=0$, and $ x=0$

Answer

$alt$

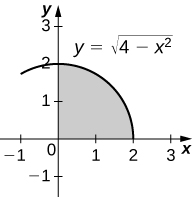
$V = \dfrac{16π}{3}$ units³

Exercise $\PageIndex{29}$

$y= \dfrac{1}{\sqrt{x+1}},\, x=o$, and $ x=3$

Answer: TBD

Exercise $\PageIndex{30}$

$ x=\sec(y)$, $y=\dfrac{\pi}{4},\, y=0$, and $ x=0$

Answer

$alt$

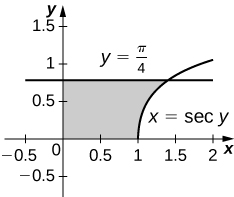
$V = π$ units³

Exercise $\PageIndex{31}$

$y=\dfrac{1}{x+1},\, x=0$, and $ x=2$

Answer: TBD

Exercise $\PageIndex{32}$

$ y=4−x,\quad y=x,$ and $ x=0$

Answer

$alt$

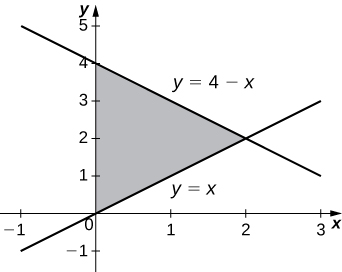
$V = \dfrac{16π}{3}$ units³

For exercises 33 - 40, draw the region bounded by the curves. Then, find the volume when the region is rotated around the $x$-axis.

Exercise $\PageIndex{33}$

$ y=x+2,\quad y=x+6,\quad x=0$, and $ x=5$

Answer: TBD

Exercise $\PageIndex{34}$

$ y=x^2$ and $ y=x+2$

Answer

$alt$

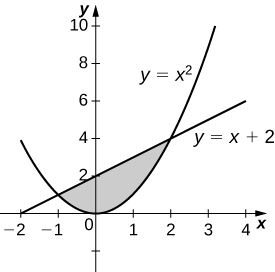
$V = \dfrac{72π}{5}$ units³

Exercise $\PageIndex{35}$

$ x^2=y^3$ and $ x^3=y^2$

Answer: TBD

Exercise $\PageIndex{36}$

$ y=4−x^2$ and $ y=2−x$

Answer

$alt$

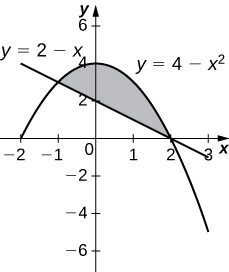
$V = \dfrac{108π}{5}$ units³

Exercise $\PageIndex{37}$

$y=\cos(x),\, y=e^{-x}, \, x=0$, and $ x=1.2927$

Answer: TBD

Exercise $\PageIndex{38}$

$y=\sqrt{x}$ and $ y=x^2$

Answer

$alt$

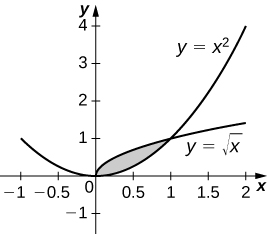
$V = \dfrac{3π}{10}$ units³

Exercise $\PageIndex{39}$

$ y=\sin x,\quad y=5\sin x,\quad x=0$ and $ x=π$

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{40}$

$y=\sqrt{1+x^2}$ and $y=\sqrt{4-x^2} $

Answer

$alt$

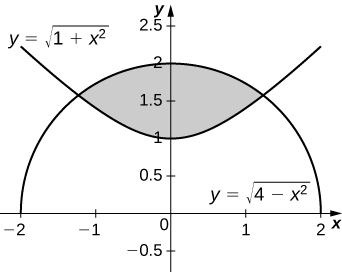
$V = 2\sqrt{6}π$ units³

For exercises 41 - 45, draw the region bounded by the curves. Then, use the washer method to find the volume when the region is revolved around the $y$-axis.

Exercise $\PageIndex{41}$

$y= \sqrt{x}, \, x=4$, and $ y=0$

Answer: TBD

Exercise $\PageIndex{42}$

$ y=x+2,\quad y=2x−1$, and $ x=0$

Answer

$alt$

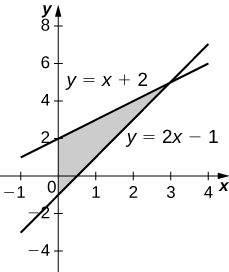
$V = 9π$ units³

Exercise $\PageIndex{43}$

$y=\dfrac{3}{x}$ and $ y=x^3$

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{44}$

$ x=e^{2y},\quad x=y^2,\quad y=0$, and $ y=\ln(2)$

Answer

$alt$

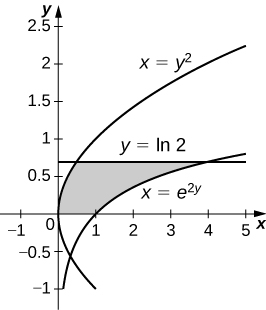
$V = \dfrac{π}{20}(75−4\ln^5(2))$ units³

Exercise $\PageIndex{45}$

$ x=\sqrt{9-y^2},\, x=e^{-y}, \, y=0$, and $ y=3$

Answer: TBD

Exercise $\PageIndex{46}$

Yogurt containers can be shaped like frustums. Rotate the line $ y= \dfrac{1}{m} x$ around the $y$-axis to find the volume between $ y=a$ and $ y=b$.

$alt$

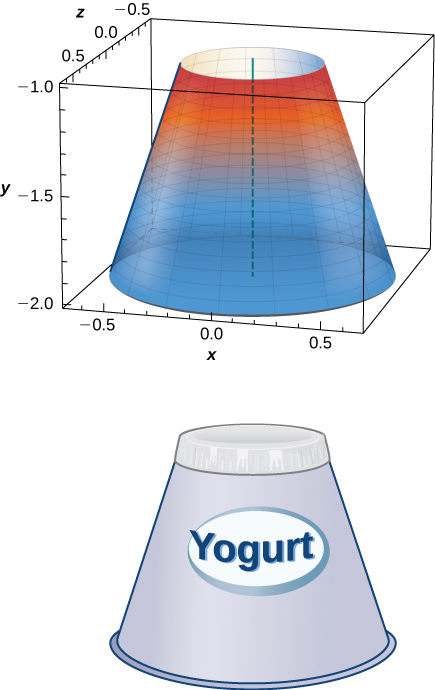
Answer: $V = \dfrac{m^2π}{3}(b^3−a^3)$ units³

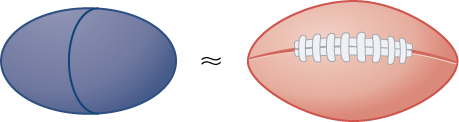
Exercise $\PageIndex{47}$

Rotate the ellipse $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ around the $x$-axis to approximate the volume of a football, as seen here.

$alt$

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{48}$

Rotate the ellipse $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ around the $y$-axis to approximate the volume of a football.

Answer: $V = \dfrac{4a^2bπ}{3}$ units³

Exercise $\PageIndex{49}$

A better approximation of the volume of a football is given by the solid that comes from rotating $ y=\sin x $ around the $x$-axis from $ x=0$ to $ x=π$. What is the volume of this football approximation, as seen here?

$alt$

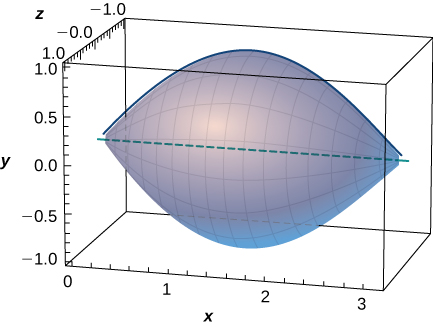
Answer: $\dfrac{\pi^2}{2} $ cubic units.

Exercise $\PageIndex{50}$

What is the volume of the Bundt cake that comes from rotating $ y=\sin x$ around the $y$-axis from $ x=0$ to $ x=π$?

$alt$

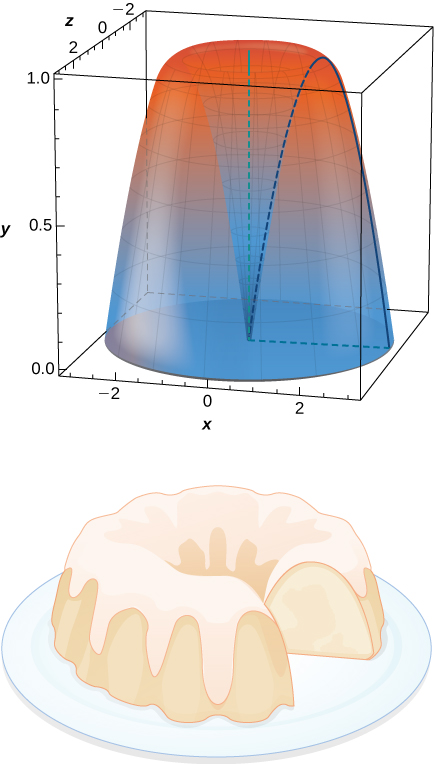
Answer: $V = 2π^2$ units³

For exercises 51 - 56, find the volume of the solid described.

Exercise $\PageIndex{51}$

The base is the region between $ y=x$ and $ y=x^2$. Slices perpendicular to the $x$-axis are semicircles.

Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{52}$

The base is the region enclosed by the generic ellipse $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ Slices perpendicular to the $x$-axis are semicircles.

Answer: $V = \dfrac{2ab^2π}{3}$ units³

Exercise $\PageIndex{53}$

Bore a hole of radius a down the axis of $a$ right cone and through the base of radius $b$, as seen here.

$alt$

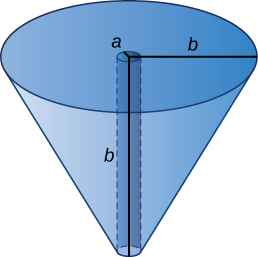
Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{54}$

Find the volume common to two spheres of radius $r$ with centers that are $2h$ apart, as shown here.

$alt$

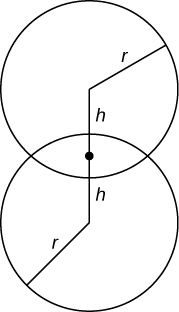
Answer: $V = \dfrac{π}{12}(r+h)^2(6r−h)$ units³

Exercise $\PageIndex{55}$

Find the volume of a spherical cap of height $h$ and radius $r$ where $h<r$, as seen here.

$alt$

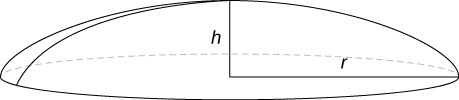
Answer: Add texts here. Do not delete this text first.

Exercise $\PageIndex{56}$

Find the volume of a sphere of radius $R$ with a cap of height $h$ removed from the top, as seen here.

$alt$

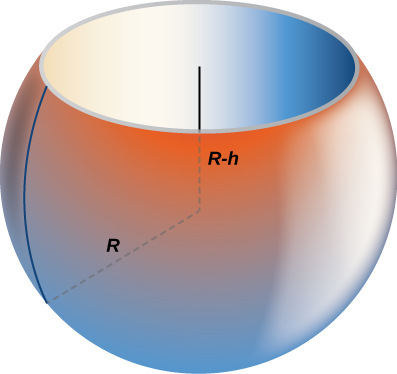
Answer: $V = \dfrac{π}{3}(h+R)(h−2R)^2$ units³