5.4: Counting Methods

Learning Objectives

Students will be able to:

• Apply the multiplication rule to quickly count the number of possible outcomes.
• Count the number of different possible arrangements by using the permutation rule.
• Count the number of different possible groupings by using the combinations rule.

Recall that

\[P(A)=\frac{\text { number of ways for } A \text { to occur }}{\text { total number of outcomes }}\]

for theoretical probabilities. So far the problems we have looked at had rather small total number of outcomes. We could easily count the number of elements in the sample space. If there are a large number of elements in the sample space we can use counting techniques such as permutations or combinations to count them.

Multiplication Principle and Tree Diagrams

The simplest of the counting techniques is the multiplication principle. A tree diagram is a useful tool for visualizing the multiplication principle.

Example \(\PageIndex{1}\): Multiplication Principle for a Three Course Dinner

Let’s say that a person walks into a restaurant for a three course dinner. There are four different salads, three different entrees, and two different desserts to choose from. Assuming the person wants to eat a salad, an entrée and a desert, how many different meals are possible?

Solution

Figure \(\PageIndex{1}\): Tree Diagram for Three-Course Dinner

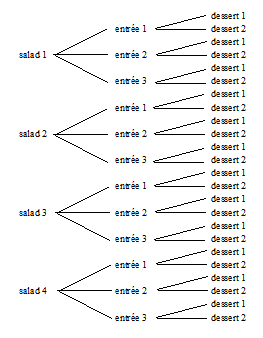
Looking at the tree diagram we can see that the total number of meals is \(4 \times 3 \times 2 = 24\, \text{meals}\).

Definition: Multiplication Principle

If there are \(n_1\) ways to of choosing the first item, \(n_2\) ways of choosing the second item after the first item is chosen, \(n_3\) ways of choosing the third item after the first two have been chosen, and so on until there are \(n_k\) ways of choosing the last item after the earlier choices, then the total number of choices overall is given by

\[n_1 \times n_2 \times n_3 \times n_4 \times n_5 ... \times n_k. \label{Multiplication Principle}\]

Example \(\PageIndex{2}\): Multiplication Principle for Lining up People

Let’s look at the number of ways that four people can line up. We can choose any of the four people to be first. Then there are three people who can be second and two people who can be third. At this point there is only one person left to be last. Using the multiplication principle there are

\[4 \times 3 \times 2 \times 1 = 24\, \text{ways} \nonumber\]

for four people to line up.

This type of calculation occurs frequently in counting problems so we have some notation to simplify the problem.

Definition: Factorial

The factorial of \(n\), read “n factorial” is

\[n! = n(n-1)(n-2)(n-3)...(2)(1).\]

By this definition, \(0! = 1.\)

Example \(\PageIndex{3}\): Factorials

\[\begin{align*} 5! &= 5 \times 4 \times 3 \times 2 \times 1 \\[4pt] &= 120 \\[5pt] 8! &= 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \\[4pt] &= 40,320 \end{align*}\]

Factorials get very large very fast.

\[20! = 2.43 \times 10^{18} \nonumber\]

and

\[40! = 8.16 \times 10^{47}. \nonumber\]

70! is larger than most calculators can handle.

The multiplication principle may seem like a very simple idea but it is very powerful. Many complex counting problems can be solved using the multiplication principle.

Example \(\PageIndex{4}\): Multiplication Principle for License Plates

Some license plates in Arizona consist of three digits followed by three letters. How many license plates of this type are possible if:

1. There are 10 digits (0, 1, 2, 3, …, 9) and 26 letters. \[\underbrace{(10 \cdot 10 \cdot 10) \cdot (26 \cdot 26 \cdot 26)}_{\text{digits}}=17,576,000 \text {license plates } \nonumber\]
2. letters can be repeated but digits cannot? \[\underbrace{(\underline{10} \cdot \underline{9} \cdot \underline{8}) \cdot(26 \cdot 26 \cdot 26)}_{\text {letters}}=12,654,720\, \text{license plates} \nonumber\]
3. the first digit cannot be zero and both digits and letters can be repeated? \[\underbrace{(\underline{9} \cdot \underline{10} \cdot \underline{10})}_{\text{digits}} \cdot \underbrace{(\underline{26} \cdot 26 \cdot 26)}_{\text{letters}}=15,818,400\, \text{license plates} \nonumber\]
4. neither digits nor numbers can be repeated. \[\underbrace{(\underline{10} \cdot \underline{9} \cdot \underline{8})}_{\text{digits}} \cdot \underbrace{(\underline{26} \cdot \underline{25} \cdot \underline{24})}_{\text{letters}}=11,232,000 \, \text{license plates} \nonumber\]

Permutations

Consider the following counting problems:

1. In how many ways can three runners finish a race?
2. In how many ways can a group of three people be chosen to work on a project?

What is the difference between these two problems? In the first problem the order that the runners finish the race matters. In the second problem the order in which the three people are chosen is not important, only which three people are chosen matters.

Definition: Permutation

A permutation is an arrangement of a set of items. The number of permutations of n items taking r at a time is given by:​​​

\[P(n, r)=\frac{n !}{(n-r) !} \label{permutation}\]

Note: Many calculators can calculate permutations directly. Look for a function that looks like \(_nP_r\) or \(P(n,r)\)

Example \(\PageIndex{5}\): Permutation for Race Cars

Let’s look at a simple example to understand the formula for the number of permutations of a set of objects. Assume that 10 cars are in a race. In how many ways can three cars finish in first, second and third place? The order in which the cars finish is important. Use the multiplication principle. There are 10 possible cars to finish first. Once a car has finished first, there are nine cars to finish second. After the second car is finished, any of the eight remaining cars can finish third. 10 x 9 x 8 = 720. This is a permutation of 10 items taking three at a time.

Using the permutation formula (Equation \ref{permutation}):

\[P(10,3)=\frac{10 !}{(10-3) !}=\frac{10 !}{7 !}= \dfrac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 10 \cdot 9 \cdot 8 = 720 \nonumber\]

Using the multiplication principle (Equation \ref{Multiplication Principle}):

\[\underline{10} \cdot \underline{9} \cdot \underline{8} = 720 \nonumber\]

There are 720 different ways for cars to finish in the top three places.

Example \(\PageIndex{6}\): Permutation for Orchestra Programs

The school orchestra is planning to play six pieces of music at their next concert. How many different programs are possible?

Solution

This is a permutation because they are arranging the songs in order to make the program. Using the permutation formula (Equation \ref{permutation}):

\[P(6,6)=\frac{6 !}{(6-6) !}=\frac{6 !}{0 !}=\frac{720}{1}=720 \nonumber\]

Using the multiplication principle (Equation \ref{Multiplication Principle}):

\[\underline{6} \cdot \underline{5} \cdot \underline{4} \cdot \underline{3} \cdot \underline{2} \cdot \underline{1}=720 \nonumber\]

There are 720 different ways of arranging the songs to make the program.

Example \(\PageIndex{7}\): Permutation for Club Officers

The Volunteer Club has 18 members. An election is held to choose a president, vice-president and secretary. In how many ways can the three officers be chosen?

Solution

The order in which the officers are chosen matters so this is a permutation.

Using the permutation formula (Equation \ref{permutation}):

\[P(18,3)=\frac{18 !}{(18-3) !}=\frac{18 !}{15 !}=18 \cdot 7 \cdot 6=4896 \nonumber\]

Note: All digits in 18! in the numerator from 15 down to one will cancel with the 15! in the denominator.

Using the multiplication principle (Equation \ref{Multiplication Principle}):

\(\begin{array} {cccccc} {\underline{18}}&{\cdot}&{\underline{17}}&{\cdot}&{\underline{16}}&{ = 4896}\\ {\text{Pres.}}&{}&{\text{V.P.}}&{}&{\text{Sec.}}&{} \end{array}\)

There are 4896 different ways the three officers can be chosen.

Another notation for permutations is \(_nP_r\). So, \(P(18,3)\) can also be written as \(_{18}P_3\). Most scientific calculators have an \(_nP_r\) button or function.

Combinations

Example \(\PageIndex{8}\): Formula for Combinations

Choose a committee of two people from persons A, B, C, D and E. By the multiplication principle there are \*5 \cdot 4 = 20\) ways to arrange the two people.

AB AC AD AE BA BC BD BE CA CB

CD CE DA DB DC DE EA EB EC ED

Committees AB and BA are the same committee. Similarly for committees CD and DC. Every committee is counted twice.

\[\frac{20}{2}=10 \nonumber\]

so there are 10 possible different committees.

Now choose a committee of three people from persons A, B, C, D and E. There are \(5 \cdot 4 \cdot 3 = 60\) ways to pick three people in order. Think about the committees with persons A, B and C. There are \(3! =6\) of them.

ABC ACB BAC BCA CAB CBA

Each of these is counted as one of the 60 possibilities but they are the same committee. Each committee is counted six times so there are

\[\frac{60}{6}=10 \, \text{different committees}. \nonumber\]

In both cases we divided the number of permutations by the number of ways to rearrange the people chosen.

The number of permutations of n people taking r at a time is \(P(n,r)\) and the number of ways to rearrange the people chosen is \(r!\). Putting these together we get

\[\begin{aligned}
\frac{n !}{\# \text { ways to arrange r items }} &=\frac{P(n, r)}{r !}=\frac{(n-r) !}{\frac{r !}{1}} \\
&=\frac{n !}{(n-r) !} \cdot \frac{1}{r !} \\
&=\frac{n !}{(n-r) ! r !}
\end{aligned}\]

Definition: Combination

A combination is a selection of objects in which the order of selection does not matter. The number of combinations of n items taking r at a time is:

\[C(n, r)=\frac{n !}{r !(n-r) !} \label{combination}\]

Note: Many calculators can calculate combinations directly. Look for a function that looks like \(_nC_r\) or (C(n,r)).

Example \(\PageIndex{9}\): Combination for Picking Books

A student has a summer reading list of eight books. The student must read five of the books before the end of the summer. In how many ways can the student read five of the eight books?

Solution

The order of the books is not important, only which books are read. This is a combination of eight items taking five at a time.

\[C(8,5)=\frac{8 !}{5 !(8-5) !}=\frac{8 !}{5 ! 3 !}= \dfrac{8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{5 \times 4 \times 3 \times 2 \times 1} = \dfrac{8 \times 7 \times 6}{3 \times 2 \times 1} = 8 \times 7 = 56\]

There are 56 ways to choose five of the books to read.

Example \(\PageIndex{10}\): Combination for Halloween Candy

A child wants to pick three pieces of Halloween candy to take in her school lunch box. If there are 13 pieces of candy to choose from, how many ways can she pick the three pieces?

Solution

This is a combination because it does not matter in what order the candy is chosen.

\[\begin{align*} C(13,3) &=\frac{13 !}{3 !(13-3) !}=\frac{13 !}{3 ! 10 !} \\[4pt] &= \dfrac{13 \times 12 \times 11 \times 10 \times 9\times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1}{(3 \times 2 \times 1)(10 \times 9\times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1} \\[4pt] &=\frac{13 \times 12 \times 11}{3 \times 2 \times 1} \\[4pt] =\frac{1716}{6}=286 \end{align*}\]

There are 286 ways to choose the three pieces of candy to pack in her lunch.

Note: The difference between a combination and a permutation is whether order matters or not. If the order of the items is important, use a permutation. If the order of the items is not important, use a combination.

Example \(\PageIndex{11}\): Permutation or Combination for Bicycle Serial Numbers

A serial number for a particular model of bicycle consists of a letter followed by four digits and ends with two letters. Neither letters nor numbers can be repeated. How many different serial numbers are possible?

Solution

This is a permutation because the order matters.

Use the multiplication principle to solve this. There are 26 letters and 10 digits possible.

\[26 \cdot 10 \cdot \underline{9} \cdot \underline{8} \cdot \underline{7} \cdot \underline{25} \cdot \underline{24}=78,624,000\]

There are 78,624,000 different serial numbers of this form.

Example \(\PageIndex{12}\): Permutation or Combination for Choosing Men and Women

A class consists of 15 men and 12 women. In how many ways can two men and two women be chosen to participate in an in-class activity?

Solution

This is a combination since the order in which the people is chosen is not important.

Choose two men:

\[C(15,2)=\frac{15 !}{2 !(15-2) !}=\frac{15 !}{2 ! 13 !}=105 \nonumber\]

Choose two women:

\[C(12,2)=\frac{12 !}{2 !(12-2) !}=\frac{12 !}{2 ! 10 !}=66 \nonumber\]

We want 2 men and 2 women so multiply these results.

\[105(66)=6930 \nonumber\]

There are 6930 ways to choose two men and two women to participate.

Probabilities Involving Permutations and Combinations

Now that we can calculate the number of permutations or combinations, we can use that information to calculate probabilities.

Example \(\PageIndex{13}\): Probability with a Combination for Choosing Students

There are 20 students in a class. Twelve of the students are women. The names of the students are put into a hat and five names are drawn. What is the probability that all of the chosen students are women?

Solution

This is a combination because the order of choosing the students is not important.

\[P(\text { all females })=\frac{\# \text { ways to pick } 5 \text { women }}{\# \text { ways to pick } 5 \text { students }}\]

The number of way to choose 5 women is

\[C(12,5)=792 \nonumber\]

The number of ways to choose 5 students is

\[C(20,5)=15,504 \nonumber\]

\[P(\text { all females })=\frac{\# \text { ways to pick } 5 \text { women }}{\# \text { ways to pick } 5 \text { students }}=\frac{792}{15,504}=0.051 \nonumber\]

The probability that all the chosen students are women is 0.051 or 5.1%.

Example \(\PageIndex{14}\): Probability with a Permutation for a Duck Race

The local Boys and Girls Club holds a duck race to raise money. Community members buy a rubber duck marked with a numeral between 1 and 30, inclusive. The box of 30 ducks is emptied into a creek and allowed to float downstream to the finish line. What is the probability that ducks numbered 5, 18 and 21 finish in first, second and third, respectively?

Solution

This is a permutation since the order of finish is important.

\[P(5,18 \& 21 \text { finish } 1 \text { st, } 2 \text { nd } \& \text { 3 } \mathrm{rd})=\dfrac{\# \text { ways } 5,18 \& 21 \text { finish } 1 \text { st, } 2 \text { nd } \& 3 \mathrm{rd}}{\# \text { ways any ducks can finish } 1 \text { st, } 2 \text { nd } \& \text { 3rd }} \nonumber\]

There is only one way that the ducks can finish with #5 in first, #18 in second and #21 in third.

The number of ways any ducks can finish in first, second and third is

\[P(30,3)=24,360 \nonumber\]

\[ \begin{align*} P(5,18 \& 21 \text { finish } 1 \text { st, } 2 \text { nd } \& \text {3rd}) &=\frac{\# \text { ways } 5,18 \& 21 \text { finish } 1 \text { st, } 2 \text { nd } \& 3 \text { rd }}{\# \text { ways any ducks can finish } 1 \text {st,}, 2 \text {nd} \& \text {3 rd}} \\[4pt] &=\frac{1}{24,360} \approx 4.10 x 10^{-5} \end{align*}\]

The probability that ducks numbered 5, 18 and 21 finish in first, second and third, respectively, is approximately 0.000041 or 0.0041%.

Example \(\PageIndex{15}\): Probability with a Permutation for Two-Card Poker Hands

A poker hand consists of two cards. What is the probability that the poker hand consists of two jacks or two fives?

Solution

It’s not possible to get two jacks and two fives at the same time so these are mutually exclusive events.

The number of ways to get two jacks is

\[C(4,2)=6.\]

The number of ways to get two fives is

\[C(4,2)=6\]

The number of ways to get two jacks or two fives is

\[6+6=12\]

The total number of ways to get a 2-card poker hand is

\[C(52,2)=1326\]

\[P(2 \text { jacks or } 2 \text { fives })=\dfrac{\text { number of ways to get } 2 \text { jacks or } 2 \text { fives }}{\text { number of ways to choose } 2 \text { cards }}=\frac{12}{1326} \approx 0.009\]

The probability of getting two jacks or two fives is approximately 0.009 or 0.9%.

Example \(\PageIndex{16}\): Probability with a Combination for Rotten Apples

A basket contains 10 good apples and two bad apples. If a distracted shopper reaches into the basket and picks three apples without looking, what is the probability he gets one bad apple?

Solution

This is a combination since the order in which the apples were picked is not important. He picks three apples total. If one apple is bad the other two must be good. Find the probability of one bad apple and two good apples.

\[P(\text { one bad and two good apples })=\frac{\# \text { ways to get one bad and two good apples }}{\# \text { ways to get three apples }} \nonumber\]

The number of ways to get one bad and two good apples is

\[C(2,1) \cdot C(10,2)=2 \cdot 45=90 \nonumber\]

The number of ways to get three apples is

\[C(10,3)=120\]

\[ \begin{align*} P(\text { one bad and two good apples }) &=\frac{\# \text { ways to get one bad and two good apples }}{\# \text { ways to get three apples }} \\[4pt] &=\frac{90}{120} \\[4pt] &=0.75 \end{align*}\]

The probability of getting one bad apple out of three apples is 0.75 or 75%