2.3: Other Charts

Last updated
Save as PDF

Page ID: 105815

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Frequency and relative frequency distribution tables along with (relative) frequency bar plots and histograms are considered the basic visual summaries of data as they can be constructed for any type of data and essentially provide all the information one may need to know about the given data. However, statisticians continue to invent ways to display data. Next, we will discuss some other less common ways used to visually summarize the data.

One method, developed in the 1960s by the late Professor John Tukey of Princeton University, is called a stem-and-leaf diagram, or stemplot. Let’s consider again the ages of the presidents at the time of their inauguration. We are going to construct the stem-and-leaf diagram by first constructing a stem - the list the first digits of all possible ages and then drawing the leaves one for each president’s age.

The stem-and leaf diagram in which stem 4 has the following leaves: 9, 8, 6, 9, 7, 2, 3, 7, 7; stem 5 has the following leaves: 7, 7, 7, 8, 7, 4, 1, 0, 2, 6, 4, 1, 5, 5, 4, 1, 6, 5, 1, 4, 1, 5, 6, 2, 4; stem 6 has the following leaves: 1, 1, 8, 4, 5, 0, 2, 1, 9, 4; stem 7 has the following leaf: 0. — Figure $\PageIndex{1}$: Stem-and-leaf diagram for the ages of US presidents. (Copyright; author via source)

Once the diagram is complete, we can sort the values in each branch in increasing order:

The stem-and leaf diagram in which stem 4 has the following leaves: 2, 3, 6, 7, 7, 7, 8, 9, 9; stem 5 has the following leaves: 0, 1, 1, 1, 1, 1, 2, 2, 4, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 7, 7, 7, 7, 8; stem 6 has the following leaves: 0, 1, 1, 1, 2, 4, 4, 5, 8, 9; stem 7 has the following leaf: 0. — Figure $\PageIndex{2}$: Stem-and-leaf diagram for the ages of US presidents with leaves in ascending order. (Copyright; author via source)

When the branches are too long, we can split the branches by assigning a portion of the branch in this case values from 0-4 to one half and the values from 5-9 to the other half:

The stem-and leaf diagram in which stem 4 has the following leaves in the first row: 2, 3, 6, and the following leaves in the second row: 7, 7, 7, 8, 9, 9; stem 5 has the following leaves in the first row: 0, 1, 1, 1, 1, 1, 2, 2, 4, 4, 4, 4, 4, and the following leaves in the second: 5, 5, 5, 5, 6, 6, 6, 7, 7, 7, 7, 8; stem 6 has the following leaves in the first row: 0, 1, 1, 1, 2, 4, 4, 5, and the following leaves in the second row: 8, 9; stem 7 has the following leaf: 0. — Figure $\PageIndex{3}$: Stem-and-leaf diagram for the ages of US presidents with split stem and leaves in ascending order. (Copyright; author via source)

To construct a stem-and-leaf diagram:

Think of each observation as a stem—consisting of all but the rightmost digit—and a leaf, the rightmost digit.
Write the stems from smallest to largest in a vertical column to the left of a vertical rule.
Write each leaf to the right of the vertical rule in the row that contains the appropriate stem.
(Optional) Arrange the leaves in each row in ascending order.
(Optional) Split the stems.

This ingenious diagram is often easier to construct than either a frequency distribution or a histogram and generally displays more information.

Here are a few tips to consider before making a stem-and-leaf diagram also known as a stemplot:

Stemplots do not work well for large data sets, where each stem must hold a large number of leaves.
There is no magic number of stems to use, but five is a good minimum. Too few or too many stems will make it difficult to see the distribution’s shape.
If you split stems, be sure that each stem is assigned an equal number of possible leaf digits (two stems, each with five possible leaves; or five stems, each with two possible leaves).
You can get more flexibility by rounding the data so that the final digit after rounding is suitable as a leaf. Do this when the data has too many digits. For example, in reporting teachers’ salaries, using all five digits (for example, $42,549) would be unreasonable. It would be better to round to the nearest thousand and use 4 as a stem and 3 as a leaf.

Alternatively, we can use another type of graphical display for quantitative data called the dot plot.

The dot plot showing the horizontal axis extending from 40 to 70 and 45 dots (one for each president's age) aligned in the following way: 1 dot above 42, 1 dot above 43, 1 dot above 46, 3 dots above 47, 1 dot above 48, 2 dots above 49, 1 dot above 50, 5 dots above 51, 2 dots above 52, 5 dots above 54, 4 dots above 55, 3 dots above 56, 4 dots above 57, 1 dot above 58, 1 dot above 60, 3 dots above 61, 1 dot above 62, 2 dots above 64, 1 dot above 65, 1 dot above 68, 1 dot above 69, and 1 dot above 70. — Figure $\PageIndex{4}$: Dot plot for the ages of US presidents. (Copyright; author via source)

To Construct a Dot Plot:

Draw a horizontal axis that displays the possible values of the quantitative data.
Record each observation by placing a dot over the appropriate value on the horizontal axis.
Label the horizontal axis with the name of the variable.

Dot plots are particularly useful for showing the relative positions of the data in a data set or for comparing two or more data sets.

Why bother with learning different ways to summarize data?

The advantage of dot plots and stem-and-leaf plots is that both of them can be constructed as the data being collected, that is we do not need to have access to the entire data set to start visualizing it.
To compare two populations side-by-side we can use a back-to-back stem-and-leaf plot by drawing a stem and adding leaves for one population on one side and for the other population on the other side. We can also use the dot plot in the same way by drawing the dots for one population above the x-axis and for the other population below the x-axis.

As an alternative to drawing the vertical bars in histograms we can mark the frequencies with a point and then connect the points with lines.

A frequency polygon superimposed on a frequency histogram showing ages at inauguration of 45 US presidents of which there are 2 presidents between 40 and 45, 7 between 45-50, 13 between 50-55, 12 between 55-60, 7 between 60-65, 3 between 65-70, 1 between 70-75. — Figure $\PageIndex{5}$: Frequency Polygon Superimposed on the Frequency Histogram (on the left) and Frequency Polygon by itself (on the right) for the ages of US presidents.

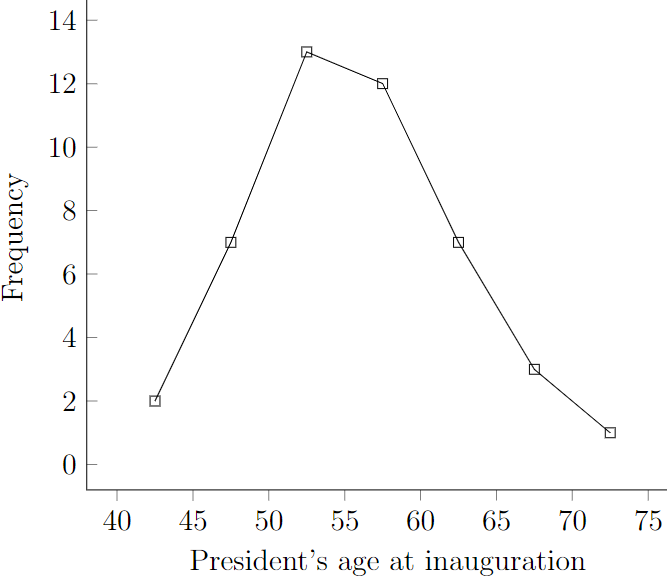
A frequency polygon showing ages at inauguration of 45 US presidents of which there are 2 presidents between 40 and 45, 7 between 45-50, 13 between 50-55, 12 between 55-60, 7 between 60-65, 3 between 65-70, 1 between 70-75. — Figure $\PageIndex{5}$: Frequency Polygon Superimposed on the Frequency Histogram (on the left) and Frequency Polygon by itself (on the right) for the ages of US presidents.

Such a summary is called a frequency polygon. As an alternative it can be used to save ink in your printer!

Another common way to organize the data is to use a cumulative frequency. A cumulative frequency of a class is obtained by summing the frequencies of all classes representing values less than the upper limit of the given class. The last entry in the cumulative frequency column must be equal to the total number of observations.

Cumulative Frequency Table for presidents' ages at inauguration
Classes	Midpoint	Frequency	Cumulative Frequency
40 to 45	42.5	2	2
45 to 50	47.5	7	2+7=9
50 to 55	52.5	13	2+7+13=22
55 to 60	57.5	12	2+7+13+12=34
60 to 65	62.5	7	2+7+13+12+7=41
65 to 70	67.5	3	2+7+13+12+7+3=44
70 to 75	72.5	1	2+7+13+12+7+3+1=45
Total:		45

A cumulative frequency polygon that is constructed using the midpoints on the horizontal axis and the cumulative frequency on the vertical axis is called ogive.

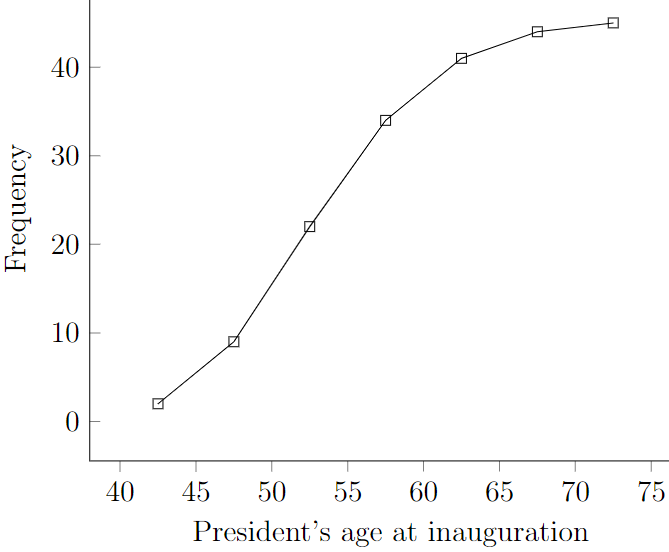
A cumulative frequency polygon showing ages at inauguration of 45 US presidents of which there are 2 presidents are younger than 45, 9 are younger than 50, 22 are younger than 55, 34 are younger than 60, 41 are younger than 65, 44 are younger than 70, and all 45 are younger than 75. — Figure $\PageIndex{6}$: Cumulative Frequency Polygon for the ages of US presidents. (Copyright; author via source)

We can easily do the same with relative cumulative frequencies. First construct the cumulative relative frequency table:

Cumulative relative frequency table for the ages of US presidents.
Classes	Midpoint	Cumulative Frequency	Relative Cumulative Frequency
40 to 45	42.5	2	2/45=0.044
45 to 50	47.5	9	9/45=0.200
50 to 55	52.5	22	22/45=0.489
55 to 60	57.5	34	34/45=0.756
60 to 65	62.5	41	41/45=0.911
65 to 70	67.5	44	44/45=0.978
70 to 75	72.5	45	45/45=1.000

Then construct the cumulative relative frequency polygon, also known as ogive:

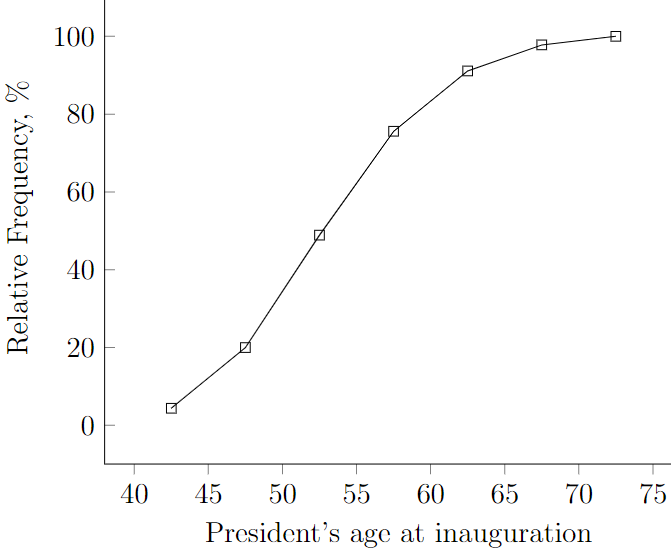
A relative cumulative frequency polygon showing ages at inauguration of 45 US presidents of which there are 4.4% are younger than 45, 20% are younger than 50, 48.9% are younger than 55, 75.6% are younger than 60, 91.1% are younger than 65, 97.8% are younger than 70, and all 100% are younger than 75. — Figure $\PageIndex{7}$: Ogive for the ages of US presidents. (Copyright; author via source)

We discussed a variety of alternatives to the most basic visual summaries – frequency tables and histograms.

Search

Text Color

Text Size

Margin Size

Font Type