1.6E: Inverse Functions

Last updated
Save as PDF

Page ID: 127010

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

section 1.6 exercises

Assume that the function f is a one-to-one function.

1. If $f(6)=7$, find $f^{-1} (7)$

2. If $f(3)=2$, find $f^{-1} (2)$

3. If $f^{-1} (-4)=-8$, find $f(-8)$

4. If $f^{-1} (-2)=-1$, find $f(-1)$

5. If $f(5)=2$, find $(f(5))^{-1}$

6. If $f(1)=4$, find $(f(1))^{-1}$

7. Using the graph of $f(x)$ shown

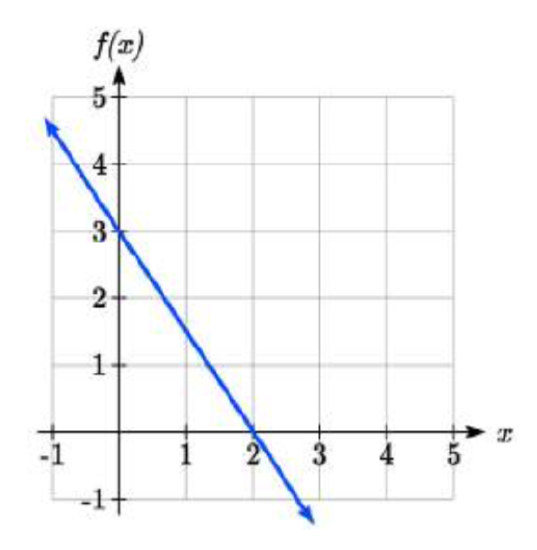
$屏幕快照 2019-06-17 下午5.06.51.png$

a. Find $f(0)$

b. Solve $f(x)=0$

c. Find $f^{-1} (0)$

d. Solve $f^{-1} (x)=0$

8. Using the graph shown

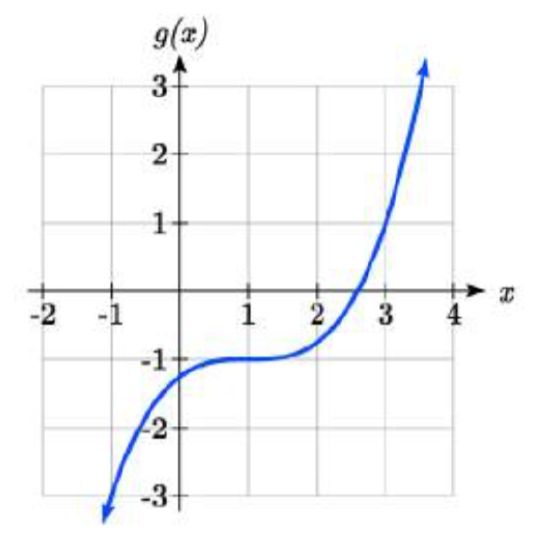
$屏幕快照 2019-06-17 下午5.08.02.png$

a. Find $g(1)$

b. Solve $g(x)=1$

c. Find $g^{-1} (1)$

d. Solve $g^{-1} (x)=1$

9. Use the table below to find the indicated quantities.

$x$	0	1	2	3	4	5	6	7	8	9
$f(x)$	8	0	7	4	2	6	5	3	9	1

a. Find $f(1)$

b. Solve $f(x)=3$

c. Find $f^{-1}(0)$

d. Solve $f^{-1}(x)=7$

10. Use the table below to fill in the missing values.

$t$	0	1	2	3	4	5	6	7	8
$h(t)$	6	0	1	7	2	3	5	4	9

a. Find $h(6)$

b. Solve $h(t)=0$

c. Find $h^{-1} (5)$

d. Solve $h^{-1} (t)=1$

For each table below, create a table for $f^{-1} (x).$

11.

$x$	3	6	9	13	14
$f(x)$	1	4	7	12	16

For each function below, find $f^{-1} (x)$

13. $f(x)=x+3$

14. $f(x)=x+5$

15. $f(x)= 2 - x$

16. $f(x)=3-x$

17. $f(x)=11x+7$

18. $f(x)=9+10x$

For each function, find a domain on which $f$ is one-to-one and non-decreasing, then find the inverse of $f$ restricted to that domain.

19. $f(x)=(x +7)^{2}$

20. $f(x)=(x-6)^{2}$

21. $f(x)=x^{2} -5$

22. $f(x)=x^{2} +1$

23. If $f(x)=x^{3} -5$ and $g(x)=\sqrt[{3}]{x+5}$, find

a. $f(g(x))$

b. $g(f(x))$

c. What does this tell us about the relationship between $f(x)$ and $g(x)$?

24. If $f(x)=\dfrac{x}{2+x}$ and $g(x)=\dfrac{2x}{1-x}$, find

a. $f(g(x))$

b. $g(f(x))$

c. What does this tell us about the relationship between $f(x)$ and $g(x)$?

Answer

1. 6

3. -4

5. 1/2

7a. 3
b. 2
c. 2
d. 2

11.

$x$	1	4	7	12	16
$f^{-1}(x)$	3	6	9	13	14

13. $f^{-1}(x) = x -3$

15. $f^{-1}(x) = -x + 2$

17. $f^{-1}(x) = \dfrac{x - 7}{11}$

19. Restricted domain $x \ge -7$, $f^{-1}(x) = \sqrt{x} - 7$

21. Restricted domain $x \ge 0$, $f^{-1}(x) = \sqrt{x + 5}$

23a. $f(g(x)) = (\sqrt[3]{x + 5})^3 - 5 = x$
b. $g(f(x)) = \sqrt[3]{x^3 - 5 + 5} = x$
c. This means that they are inverse functions (of each other)

\(x\)	0	1	2	3	4	5	6	7	8	9
\(f(x)\)	8	0	7	4	2	6	5	3	9	1

\(t\)	0	1	2	3	4	5	6	7	8
\(h(t)\)	6	0	1	7	2	3	5	4	9

\(x\)	3	6	9	13	14
\(f(x)\)	1	4	7	12	16

\(x\)	1	4	7	12	16
\(f^{-1}(x)\)	3	6	9	13	14