5.3: Use Direct and Inverse Variation
- Last updated
- Nov 6, 2023
- Save as PDF
- Page ID
- 142722
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
By the end of this section, you will be able to:
- Solve direct variation problems
- Solve inverse variation problems
Note
Before you get started, take this readiness quiz.
If you miss a problem, go back to the section listed and review the material.
- Find the multiplicative inverse of −8
If you missed this problem, review Exercise 1.10.13. - Solve for n: 45=20n
If you missed this problem, review Exercise 2.2.1. - Evaluate 5x2 when x=10
If you missed this problem, review Exercise 1.3.25.
When two quantities are related by a proportion, we say they are proportional to each other. Another way to express this relation is to talk about the variation of the two quantities. We will discuss direct variation and inverse variation in this section.
Solve Direct Variation Problems
Lindsay gets paid $15 per hour at her job. If we let s be her salary and h be the number of hours she has worked, we could model this situation with the equation
s=15h
Lindsay’s salary is the product of a constant, 15, and the number of hours she works. We say that Lindsay’s salary varies directly with the number of hours she works. Two variables vary directly if one is the product of a constant and the other.
Definition: DIRECT VARIATION
For any two variables x and y, y varies directly with x if
y=kx, where n≠0
In applications using direct variation, generally we will know values of one pair of the variables and will be asked to find the equation that relates x and y. Then we can use that equation to find values of y for other values of x.
How to Solve Direct Variation Problems
Example 5.3.1
If y varies directly with x and y=20 when x=8, find the equation that relates x and y.
- Answer
-




Example 5.3.2
If y varies directly as x and y=3, when x=10, find the equation that relates x and y.
- Answer
-
y=310x
Example 5.3.3
If y varies directly as x and y=12 when x=4, find the equation that relates x and y.
- Answer
-
y=3x
We’ll list the steps below.
Definition: SOLVE DIRECT VARIATION PROBLEMS
- Write the formula for direct variation.
- Substitute the given values for the variables.
- Solve for the constant of variation.
- Write the equation that relates x and y.
Now we’ll solve a few applications of direct variation.
Example 5.3.4
When Raoul runs on the treadmill at the gym, the number of calories, c, he burns varies directly with the number of minutes, m, he uses the treadmill. He burned 315 calories when he used the treadmill for 18 minutes.
- Write the equation that relates c and m.
- How many calories would he burn if he ran on the treadmill for 25 minutes?
- Answer
-
1.
The number of calories, c varies directly with the number of minutes, m, on the treadmill, and c=315 when m=18 Write the formula for direct variation. 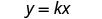
We will use c in place of y and mm in place of x. 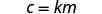
Substitute the given values for the variables. 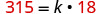
Solve for the constant of variation. 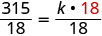
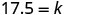
Write the equation that relates c and m. 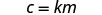
Substitute in the constant of variation. 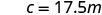
2.
Find c when m=25.
Write the equation that relates c and m. 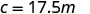
Substitute the given value for m. 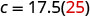
Simplify. 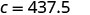
Raoul would burn 437.5 calories if he used the treadmill for 25 minutes.
Example 5.3.5
The number of calories, c, burned varies directly with the amount of time, t, spent exercising. Arnold burned 312 calories in 65 minutes exercising.
- Write the equation that relates c and t.
- How many calories would he burn if he exercises for 90 minutes?
- Answer
-
- c=4.8t
- 432 calories
Example 5.3.6
The distance a moving body travels, d, varies directly with time, t, it moves. A train travels 100 miles in 2 hours
- Write the equation that relates d and t.
- How many miles would it travel in 5 hours?
- Answer
-
- d=50t
- 250 miles
In the previous example, the variables c and m were named in the problem. Usually that is not the case. We will have to name the variables in the next example as part of the solution, just like we do in most applied problems.
Example 5.3.7
The number of gallons of gas Eunice’s car uses varies directly with the number of miles she drives. Last week she drove 469.8 miles and used 14.5 gallons of gas.
- Write the equation that relates the number of gallons of gas used to the number of miles driven.
- How many gallons of gas would Eunice’s car use if she drove 1000 miles?
- Answer
-
1.
The number of gallons of gas varies directly with the number of miles driven. First we will name the variables. Let g= number of gallons of gas.
m= number of miles driven.Write the formula for direct variation. 
We will use g in place of y and m in place of x. 
Substitute the given values for the variables 
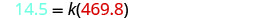
Solve for the constant of variation. 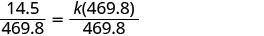
We will round to the nearest thousandth. 
Write the equation that relates g and m. 
Substitute in the constant of variation. 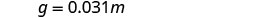
2.
Find g when m=1000. Write the equation that relates g and m. g=0.031m Substitute the given value for m. g=0.031(1000) Simplify. g=31 Eunice’s car would use 31 gallons of gas if she drove it 1,000 miles. Notice that in this example, the units on the constant of variation are gallons/mile. In everyday life, we usually talk about miles/gallon.
Example 5.3.8
The distance that Brad travels varies directly with the time spent traveling. Brad travelled 660 miles in 12 hours,
- Write the equation that relates the number of miles travelled to the time.
- How many miles could Brad travel in 4 hours?
- Answer
-
- m=55h
- 220 miles
Example 5.3.9
The weight of a liquid varies directly as its volume. A liquid that weighs 24 pounds has a volume of 4 gallons.
- Write the equation that relates the weight to the volume.
- If a liquid has volume 13 gallons, what is its weight?
- Answer
-
- w=6v
- 78 pounds
In some situations, one variable varies directly with the square of the other variable. When that happens, the equation of direct variation is y=kx2.
Example 5.3.10
The maximum load a beam will support varies directly with the square of the diagonal of the beam’s cross-section. A beam with diagonal 4” will support a maximum load of 75 pounds.
- Write the equation that relates the maximum load to the cross-section.
- What is the maximum load that can be supported by a beam with diagonal 8”?
- Answer
-
1.
The maximum load varies directly with the square of the diagonal of the cross-section. Name the variables. Let L= maximum load.
c= the diagonal of the cross-sectionWrite the formula for direct variation, where y varies directly with the square of x. 
We will use L in place of y and c in place of x. 
Substitute the given values for the variables. 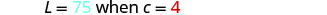

Solve for the constant of variation. 

Write the equation that relates L and c. 
Substitute in the constant of variation. 
2.
Find L when c=8. Write the equation that relates L and c. L=4.6875c2 Substitute the given value for c. L=4.6875(8)2 Simplify. L=300 A beam with diagonal 8” could supporta maximum load of 300 pounds.
Example 5.3.11
The distance an object falls is directly proportional to the square of the time it falls. A ball falls 144 feet in 3 seconds.
- Write the equation that relates the distance to the time.
- How far will an object fall in 4 seconds?
- Answer
-
- d=16t2
- 256 feet
Example 5.3.12
The area of a circle varies directly as the square of the radius. A circular pizza with a radius of 6 inches has an area of 113.04 square inches.
- Write the equation that relates the area to the radius.
- What is the area of a pizza with a radius of 9 inches?
- Answer
-
- A=3.14r2
- 254.34 square inches
Solve Inverse Variation Problems
Many applications involve two variable that vary inversely. As one variable increases, the other decreases. The equation that relates them is y=kx.
Definition: INVERSE VARIATION
For any two variables x and y, y varies inversely with x if
y=kx,where k≠0
The word ‘inverse’ in inverse variation refers to the multiplicative inverse. The multiplicative inverse of x is 1x.
We solve inverse variation problems in the same way we solved direct variation problems. Only the general form of the equation has changed. We will copy the procedure box here and just change ‘direct’ to ‘inverse’.
Definition: SOLVE INVERSE VARIATION PROBLEMS
- Write the formula for inverse variation.
- Substitute the given values for the variables.
- Solve for the constant of variation.
- Write the equation that relates x and y.
Example 5.3.13
If y varies inversely with x and y=20 when x=8 x and y.
- Answer
-
Write the formula for inverse variation. 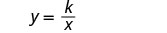
Substitute the given values for the variables. 

Solve for the constant of variation. 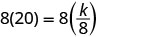

Write the equation that relates x and y. 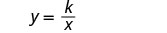
Substitute in the constant of variation. 
Example 5.3.14
If p varies inversely with q and p=30 when q=12 find the equation that relates p and q.
- Answer
-
p=360q
Example 5.3.15
If y varies inversely with x and y=8 when x=2 find the equation that relates x and y.
- Answer
-
y=16x
Example 5.3.16
The fuel consumption (mpg) of a car varies inversely with its weight. A car that weighs 3100 pounds gets 26 mpg on the highway.
- Write the equation of variation.
- What would be the fuel consumption of a car that weighs 4030 pounds?
- Answer
-
1.
The fuel consumption varies inversely with the weight. First we will name the variables. Let f= fuel consumption.
w= weight.Write the formula for inverse variation. 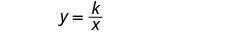
We will use f in place of y and w in place of x. 
Substitute the given values for the variables. 
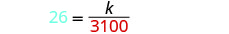
Solve for the constant of variation. 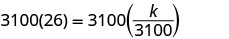

Write the equation that relates f and w. 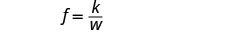
Substitute in the constant of variation. 
2.
Find f when w=4030. Write the equation that relates f and w. 
Substitute the given value for w. f=80,6004030 Simplify. f=20 A car that weighs 4030 pounds would have fuel consumption of 20 mpg.
Example 5.3.17
A car’s value varies inversely with its age. Elena bought a two-year-old car for $20,000.
- Write the equation of variation.
- What will be the value of Elena’s car when it is 5 years old?
- Answer
-
- v=40,000a
- $8,000
Example 5.3.18
The time required to empty a pool varies inversely as the rate of pumping. It took Lucy 2.5 hours to empty her pool using a pump that was rated at 400 gpm (gallons per minute).
- Write the equation of variation.
- How long will it take her to empty the pool using a pump rated at 500 gpm?
- Answer
-
- t=1000r
- 2 hours
Example 5.3.19
The frequency of a guitar string varies inversely with its length. A 26” long string has a frequency of 440 vibrations per second.
- Write the equation of variation.
- How many vibrations per second will there be if the string’s length is reduced to 20” by putting a finger on a fret?
- Answer
-
1.
The frequency varies inversely with the length. Name the variables. Let f= frequency.
L=length.Write the formula for inverse variation. 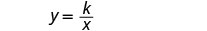
We will use f in place of y and L in place of x 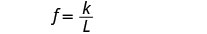
Substitute the given values for the variables. 

Solve for the constant of variation. 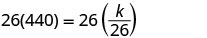

Write the equation that relates f and L. 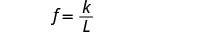
Substitute in the constant of variation. 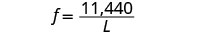
2.
Find f when L=20. Write the equation that relates f and L. f=11,440L Substitute the given value for L. f=11,44020 Simplify. f=572 A 20” guitar string has frequency 572 vibrations per second.
Example 5.3.20
The number of hours it takes for ice to melt varies inversely with the air temperature. Suppose a block of ice melts in 2 hours when the temperature is 65 degrees.
- Write the equation of variation.
- How many hours would it take for the same block of ice to melt if the temperature was 78 degrees?
- Answer
-
- h=130t
- 123 hours
Example 5.3.21
The force needed to break a board varies inversely with its length. Richard uses 24 pounds of pressure to break a 2-foot long board.
- Write the equation of variation.
- How many pounds of pressure is needed to break a 5-foot long board?
- Answer
-
- F=48L
- 9.6 pounds


