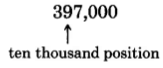Skip to main content
Mathematics LibreTexts

1.8: Rounding Whole Numbers

  1. Last updated
  2. Save as PDF
  • Page ID
    116749

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Learning Objectives

    • understand that rounding is a method of approximation
    • be able to round a whole number to a specified position

    Rounding as an Approximation

    A primary use of whole numbers is to keep count of how many objects there are in a collection. Sometimes we're only interested in the approximate number of objects in the collection rather than the precise number. For example, there are approxi­mately 20 symbols in the collection below.

    An arrangement of symbols.

    The precise number of symbols in the above collection is 18.

    Definition: Rounding

    We often approximate the number of objects in a collection by mentally seeing the collection as occurring in groups of tens, hundreds, thousands, etc. This process of approximation is called rounding. Rounding is very useful in estimation. We will study estimation in Chapter 8.

    When we think of a collection as occurring in groups of tens, we say we're rounding to the nearest ten. When we think of a collection as occurring in groups of hundreds, we say we're rounding to the nearest hundred. This idea of rounding continues through thousands, ten thousands, hundred thousands, millions, etc.

    The process of rounding whole numbers is illustrated in the following examples.

    Example \(\PageIndex{1}\)

    Round 67 to the nearest ten.

    Solution

    On the number line, 67 is more than halfway from 60 to 70. The digit immedi­ately to the right of the tens digit, the round-off digit, is the indicator for this.

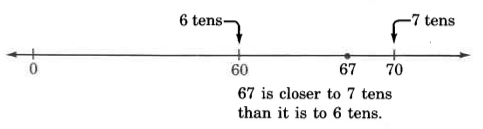
    A number line from 0 to 70. At the dash for the number sixty is a label, 6 tens. At the dash for 70 is a label, 7 tens. In between the two dashes is a dot on the number 67. Below, is a statement. 67 is closer to 7 tens than it is to 6 tens.

    Thus, 67, rounded to the nearest ten, is 70.

    Example \(\PageIndex{2}\)

    Round 4,329 to the nearest hundred.

    Solution

    On the number line, 4,329 is less than halfway from 4,300 to 4,400. The digit to the immediate right of the hundreds digit, the round-off digit, is the indicator.

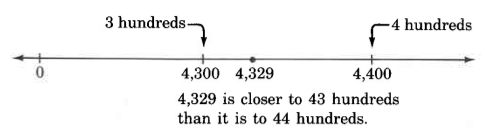
    A number line from 0 to 4,400. The mark for 4,300 is labeled, 3 hundreds. The mark for 4,400 is labeled, 4 hundreds. A dot on the number 4,329 is in between the two marks. Below the number line is a statement. 4,329 is closer to 43 hundreds than it is to 44 hundreds.

    Thus, 4,329, rounded to the nearest hundred is 4,300.

    Example \(\PageIndex{3}\)

    Round 16,500 to the nearest thousand.

    Solution

    On the number line, 16,500 is exactly halfway from 16,000 to 17,000.

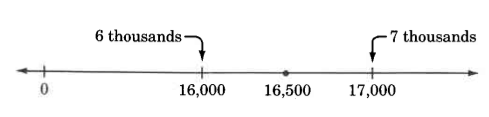
    A number line from 0 to 17,000. The 16,000 mark is labeled, 6 thousands. The 17,000 mark is labeled, 7 thousands. In between the two marks is a dot on the number 16,500.

    By convention, when the number to be rounded is exactly halfway between two numbers, it is rounded to the higher number.

    Thus, 16,500, rounded to the nearest thousand, is 17,000.

    Example \(\PageIndex{4}\)

    A person whose salary is $41,450 per year might tell a friend that she makes $41,000 per year. She has rounded 41,450 to the nearest thousand. The number 41,450 is closer to 41,000 than it is to 42,000.

    The Method of Rounding Whole Numbers

    From the observations made in the preceding examples, we can use the following method to round a whole number to a particular position.

    1. Mark the position of the round-off digit.
    2. Note the digit to the immediate right of the round-off digit.
      1. If it is less than 5, replace it and all the digits to its right with zeros. Leave the round-off digit unchanged.
      2. If it is 5 or larger, replace it and all the digits to its right with zeros. Increase the round-off digit by 1.

    Sample Set A

    Use the method of rounding whole numbers to solve the following problems.

    Round 3,426 to the nearest ten.

    Solution

    • We are rounding to the tens position. Mark the digit in the tens position
      3,426, with the 2 labeled, tens position.
    • Observe the digit immediately to the right of the tens position. It is 6. Since 6 is greater than 5, we round up by replacing 6 with 0 and adding 1 to the digit in the tens position (the round-off position): 2+1=32+1=3 .
      3,430

    Thus, 3,426 rounded to the nearest ten is 3,430.

    Sample Set A

    Round 9,614,018,007 to the nearest ten million.

    Solution

    1. We are rounding to the nearest ten million.
      9,614,018,007, with the first 1 labeled, ten millions position.
    2. Observe the digit immediately to the right of the ten millions position. It is 4. Since 4 is less than 5, we round down by replacing 4 and all the digits to its right with zeros.
      9,610,000,000

    Thus, 9,614,018,007 rounded to the nearest ten million is 9,610,000,000.

    Sample Set A

    Round 148,422 to the nearest million.

    Solution

    1. Since we are rounding to the nearest million, we'll have to imagine a digit in the millions position. We'll write 148,422 as 0,148,422.
      0,148,422, with the 0 labeled, millions position.
    2. The digit immediately to the right is 1. Since 1 is less than 5, we'll round down by replacing it and all the digits to its right with zeros.
      0,000,000
      This number is 0.

    Thus, 148,422 rounded to the nearest million is 0.

    Sample Set A

    Round 397,000 to the nearest ten thousand.

    Solution

    • We are rounding to the nearest ten thousand.
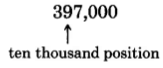
      397,000, with the 9 labeled, ten thousand position.
    • The digit immediately to the right of the ten thousand position is 7. Since 7 is greater than 5, we round up by replacing 7 and all the digits to its right with zeros and adding 1 to the digit in the ten thousands position. But 9+1=109+1=10 and we must carry the 1 to the next (the hundred thousands) position.
      400,000

    Thus, 397,000 rounded to the nearest ten thousand is 400,000.

    Practice Set A

    Use the method of rounding whole numbers to solve each problem.

    Round 3387 to the nearest hundred.

    Answer

    3400

    Practice Set A

    Round 26,515 to the nearest thousand.

    Answer

    27,000

    Practice Set A

    Round 30,852,900 to the nearest million.

    Answer

    31,000,000

    Practice Set A

    Round 39 to the nearest hundred.

    Answer

    0

    Practice Set A

    Round 59,600 to the nearest thousand.

    Answer

    60,000

    Exercises

    For the following problems, complete the table by rounding each number to the indicated positions.

    Exercise \(\PageIndex{1}\)

    1,642

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    1,600 2000 0 0

    Exercise \(\PageIndex{2}\)

    5,221

    hundred thousand ten thousand million

    Exercise \(\PageIndex{3}\)

    91,803

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    91,800 92,000 90,000 0

    Exercise \(\PageIndex{4}\)

    106,007

    hundred thousand ten thousand million

    Exercise \(\PageIndex{5}\)

    208

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    200 0 0 0

    Exercise \(\PageIndex{6}\)

    199

    hundred thousand ten thousand million

    Exercise \(\PageIndex{7}\)

    863

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    900 1,000 0 0

    Exercise \(\PageIndex{8}\)

    794

    hundred thousand ten thousand million

    Exercise \(\PageIndex{9}\)

    925

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    900 1,000 0 0

    Exercise \(\PageIndex{10}\)

    909

    hundred thousand ten thousand million

    Exercise \(\PageIndex{11}\)

    981

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    1,000 1,000 0 0

    Exercise \(\PageIndex{12}\)

    965

    hundred thousand ten thousand million

    Exercise \(\PageIndex{13}\)

    551,061,285

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    551,061,300 551,061,000 551,060,000 551,000,000

    Exercise \(\PageIndex{14}\)

    23,047,991,521

    hundred thousand ten thousand million

    Exercise \(\PageIndex{15}\)

    106,999,413,206

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    106,999,413,200 106,999,413,000 106,999,410,000 106,999,000,000

    Exercise \(\PageIndex{16}\)

    5,000,000

    hundred thousand ten thousand million

    Exercise \(\PageIndex{17}\)

    8,006,001

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    8,006,000 8,006,000 8,010,000 8,000,000

    Exercise \(\PageIndex{18}\)

    94,312

    hundred thousand ten thousand million

    Exercise \(\PageIndex{19}\)

    33,486

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    33,500 33,000 30,000 0

    Exercise \(\PageIndex{20}\)

    560,669

    hundred thousand ten thousand million

    Exercise \(\PageIndex{21}\)

    388,551

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    388,600 389,000 390,000 0

    Exercise \(\PageIndex{22}\)

    4,752

    hundred thousand ten thousand million

    Exercise \(\PageIndex{23}\)

    8,209

    hundred thousand ten thousand million
    Answer
    hundred thousand ten thousand million
    8,200 8,000 10,000 0

    Exercise \(\PageIndex{24}\)

    In 1950, there were 5,796 cases of diphtheria reported in the United States. Round to the nearest hundred.

    Exercise \(\PageIndex{25}\)

    In 1979, 19,309,000 people in the United States received federal food stamps. Round to the near­est ten thousand.

    Answer

    19,310,000

    Exercise \(\PageIndex{26}\)

    In 1980, there were 1,105,000 people between 30 and 34 years old enrolled in school. Round to the nearest million.

    Exercise \(\PageIndex{27}\)

    In 1980, there were 29,100,000 reports of aggra­vated assaults in the United States. Round to the nearest million.

    Answer

    29,000,000

    For the following problems, round the numbers to the posi­tion you think is most reasonable for the situation.

    Exercise \(\PageIndex{28}\)

    In 1980, for a city of one million or more, the average annual salary of police and firefighters was $16,096.

    Exercise \(\PageIndex{29}\)

    The average percentage of possible sunshine in San Francisco, California, in June is 73%.

    Answer

    70% or 75%

    Exercise \(\PageIndex{30}\)

    In 1980, in the state of Connecticut, $3,777,000,000 in defense contract payroll was awarded.

    Exercise \(\PageIndex{31}\)

    In 1980, the federal government paid $5,463,000,000 to Viet Nam veterans and depen­dants.

    Answer

    $5,500,000,000

    Exercise \(\PageIndex{32}\)

    In 1980, there were 3,377,000 salespeople em­ployed in the United States.

    Exercise \(\PageIndex{33}\)

    In 1948, in New Hampshire, 231,000 popular votes were cast for the president.

    Answer

    230,000

    Exercise \(\PageIndex{34}\)

    In 1970, the world production of cigarettes was 2,688,000,000,000.

    Exercise \(\PageIndex{35}\)

    In 1979, the total number of motor vehicle regis­trations in Florida was 5,395,000.

    Answer

    5,400,000

    Exercise \(\PageIndex{36}\)

    In 1980, there were 1,302,000 registered nurses the United States.

    Exercises for Review

    Exercise \(\PageIndex{37}\)

    There is a term that describes the visual displaying of a number. What is the term?

    Answer

    graphing

    Exercise \(\PageIndex{38}\)

    What is the value of 5 in 26,518,206?

    Exercise \(\PageIndex{39}\)

    Write 42,109 as you would read it.

    Answer

    Forty-two thousand, one hundred nine

    Exercise \(\PageIndex{40}\)

    Write "six hundred twelve" using digits.

    Exercise \(\PageIndex{41}\)

    Write "four billion eight" using digits.

    Answer

    4,000,000,008

    This page titled 1.8: Rounding Whole Numbers is shared under a CC BY license and was authored, remixed, and/or curated by Denny Burzynski & Wade Ellis, Jr. (OpenStax CNX) .