10.2: Rounding Integers

Rounding as an Approximation

A primary use of whole numbers is to keep count of how many objects there are in a collection. Sometimes we're only interested in the approximate number of objects in the collection rather than the precise number. For example, there are approxi­mately 20 symbols in the collection below.

The precise number of symbols in the above collection is 18.

We often approximate the number of objects in a collection by mentally seeing the collection as occurring in groups of tens, hundreds, thousands, etc. This process of approximation is one method of rounding. Rounding is very useful in estimation. When we think of a collection as occurring in groups of tens, we say we're rounding to the nearest ten. When we think of a collection as occurring in groups of hundreds, we say we're rounding to the nearest hundred. This idea of rounding continues through thousands, ten thousands, hundred thousands, millions, etc.

One Rounding Rule

Most people reading this text will be used to one rounding rule. We will think of this as the standard rounding rule. The process of rounding whole numbers using this rule is illustrated in the following examples.

Example \(\PageIndex{1}\)

Round 67 to the nearest ten.

Solution

On the number line, 67 is more than halfway from 60 to 70. The digit immedi­ately to the right of the tens digit, the round-off digit, is the indicator for this.

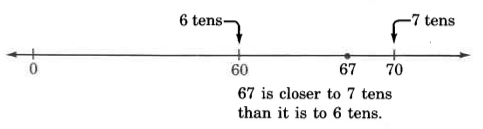
Thus, 67, rounded to the nearest ten, is 70.

Note that we can also refer to the place value when rounding. The previous example involved rounding 67 to the tens place.

Example \(\PageIndex{2}\)

Round 4,329 to the nearest hundred.

Solution

On the number line, 4,329 is less than halfway from 4,300 to 4,400. The digit to the immediate right of the hundreds digit, the round-off digit, is the indicator.

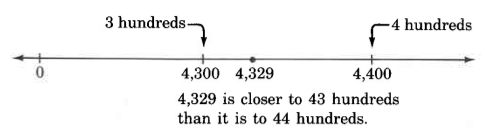
Thus, 4,329, rounded to the nearest hundred is 4,300.

Unfortunately, the word "nearest" can make rounding confusing. 

Example \(\PageIndex{3}\)

Round 16,500 to the nearest thousand.

Solution

On the number line, 16,500 is exactly halfway from 16,000 to 17,000.

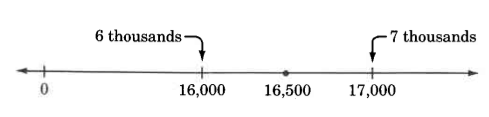
By convention, when the number to be rounded is exactly halfway between two numbers, it is rounded to the higher number.

Thus, 16,500, rounded to the nearest thousand, is 17,000.

Note the phrase "by convention" in the previous example. What that means is that the community we are discussing has made a decision (consciously or not) to do things one way. For example, by convention, we say that the letter "U" comes before the letter "V" in the English alphabet. But it does not have to be that way. It would be just as reasonable if "V" came before "U".

Most of the time, when we say "round to the nearest ____" we leave out the caveat "unless the number is exactly halfway between two values, in which case choose the larger one". This fact is merely something people decided. In fact, sometimes, we want to choose the lower value. In such cases, we must specifiy that's what we want since that's not the convention. One way a person might state this is by saying, "round down" instead of "round".

Example \(\PageIndex{4}\)

A person whose salary is $41,450 per year might tell a friend that she makes $41,000 per year. She has rounded 41,450 to the nearest thousand. The number 41,450 is closer to 41,000 than it is to 42,000.

The Method of Rounding Whole Numbers using the Standard Rule

From the observations made in the preceding examples, we can use the following method to round a whole number to a particular position.

1. Mark the position of the round-off digit.
2. Note the digit to the immediate right of the round-off digit.
   1. If it is less than 5, replace it and all the digits to its right with zeros. Leave the round-off digit unchanged.
   2. If it is 5 or larger, replace it and all the digits to its right with zeros. Increase the round-off digit by 1.

In the following example, you will see some cases that can confuse many people.

Example \(\PageIndex{1}\)

Use the method described above to do the following.

1. Round 3,426 to the nearest ten.
2. Round 9,614,018,007 to the nearest ten million.
3. Round 148,422 to the nearest million.
4. Round 397,000 to the nearest ten thousand.

Solution

1. We are rounding to the tens position. Mark the digit in the tens position.
   
   Observe the digit immediately to the right of the tens position. It is 6. Since 6 is greater than 5, we round up by replacing 6 with 0 and adding 1 to the digit in the tens position (the round-off position): 2+1=32+1=3.
   Thus, 3,426 rounded to the nearest ten is 3,430.
2. We are rounding to the nearest ten million.
   
   Observe the digit immediately to the right of the ten millions position. It is 4. Since 4 is less than 5, we round down by replacing 4 and all the digits to its right with zeros.
   Thus, 9,614,018,007 rounded to the nearest ten million is 9,610,000,000.
3. Since we are rounding to the nearest million, we'll have to imagine a digit in the millions position. We'll write 148,422 as 0,148,422.
   
   The digit immediately to the right is 1. Since 1 is less than 5, we'll round down by replacing it and all the digits to its right with zeros.
   0,000,000
   Thus, 148,422 rounded to the nearest million is 0.
4. We are rounding to the nearest ten thousand.
   
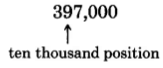
   The digit immediately to the right of the ten thousand position is 7. Since 7 is greater than 5, we round up by replacing 7 and all the digits to its right with zeros and adding 1 to the digit in the ten thousands position. But 9+1=109+1=10 and we must carry the 1 to the next (the hundred thousands) position.
   Thus, 397,000 rounded to the nearest ten thousand is 400,000.

Now try to do some on your own.

Exercise \(\PageIndex{1}\)

Use the method described above to do the following.

1. Round 3387 to the nearest hundred.
2. Round 26,515 to the nearest thousand.
3. Round 30,852,900 to the nearest million.
4. Round 39 to the nearest hundred.
5. Round 59,600 to the nearest thousand.