10.3: Rounding Decimals

Rounding Decimal Numbers

We previously considered the concept of rounding numbers where our concern with rounding was related to positive integers only. With a few minor changes, we can apply the same rules of rounding to decimals (non-integers) and negative integers. To round a value to any integer (positive or negative), we simply apply the same method as before while keeping in mind what it means for negative numbers to be less than or greater than other numbers. We have not discussed negative numbers yet, however. So, we will not focus on this at this time. So, we will focus on non-integers. The method outlined below applies to positive and negative values, but all the examples and exercises will involve positive values to keep things simple for now.

To round a decimal to a particular position:

1. Mark the position of the round-off digit.
2. Note whether the digit to the immediate right of the marked digit is
   1. less than 5. If so, leave the round-off digit unchanged.
   2. 5 or greater. If so, add 1 to the round-off digit.
3. If the round-off digit is
   1. to the right of the decimal point, eliminate all the digits to its right.
   2. to the left of the decimal point, replace all the digits between it and the decimal point with zeros and eliminate the decimal point and all the decimal digits.

Example \(\PageIndex{1}\)

Round each decimal to the specified position. (The numbers in parentheses indicate which step is being used.)

Round 32.116 to the nearest hundredth.

Solution

1.  
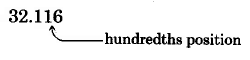
2. The digit immediately to the right is 6, and \(6 > 5\), so we add 1 to the round-off digit: \(1 + 1 = 2\).
3. The round-off digit is to the right of the decimal point, so we eliminate all digits to its right.

The number 32.116 rounded to the nearest hundredth is 32.12.

Note that the only real change to the method we saw in the previous section is that we need to consider what happens to the right of the round-off digit based on where it is in relation to the decimal point.

Example \(\PageIndex{1}\)

Round 633.14216 to the nearest hundred.

Solution

1.  
2. The digit immediately to the right is 3, and \(3 < 5\) so we leave the round-off digit unchanged.
3. The round-off digit is to the left of 0, so we replace all the digits between it and the decimal point with zeros and eliminate the decimal point and all the decimal digits.

The number 633.14216 rounded to the nearest hundred is 600.

We can actually combine 3a and 3b to the following: 3* Replace all digits to the right of the round-off digit with 0. This is because we could write literally any number as a number followed by infinitely many 0s. For example, 4.5 = 4.5000... and 670 = 670.000... The reason we usually do not do this is because by using the method with two cases for Step 3, the reader can tell exactly where our round-off digit is. Let's see what we mean by this.

Example \(\PageIndex{1}\)

Round 84.996 to the nearest hundredth using both methods (one with Steps 3a and 3b and one with Step 3*).

Solution

1. The round-off digit is the 9 in the hundredths place.
2. The digit to the right of that is 6, so we add 1 to 9. That gives us 10, so we replace the 9 with 0 and add the 1 to the digit in the tenths place. Since the digit in the tenths place is also 9, we get 10 again. So, we replace that 9 with 0 and add the 1 to the digit in the ones place. The digit in the ones place is 4, so we get 5.
3. In the first method, we eliminate the digits to the right of the round-off digit.
   Thus, 84.996 rounded to the nearest hundredth is 85.00.
   In the second method, we replace all digits to the right of the round-off digit with 0.
   Thus, 84.996 rounded to the nearest hundredth is 85.000...

Notice that in the first method, we got 85.00, and the last written 0 is in the hundredths place, which was the round-off digit! In the second method, we get 85.000..., which is equivalent in value to 85.00. But by writing it this way, the person reading our answer does not know that the hundredths place was where we rounded to unless we explicitly state that in words.

The purpose of that previous example is to give a reason for why we use the usual rounding method in which Step 3 is split into 3a and 3b. It is common for people to think, "This is unnecessarily complicated" about rules in mathematics. Sometimes it's because it has to be (in these cases, the "rules" are actually "properties"). Sometimes it's because the rule is based on a reason that may not be evident at first (like what we just saw). But there definitely are times when the "rule" is just a convention with no particular reason behind it. In those cases, there is often disagreement between mathematicians about that rule. Yes, mathematicians argue about math. They do it a lot!

Example \(\PageIndex{1}\)

Round each of the following numbers.

• 1,729.63 to the nearest ten
• 1.0144 to the nearest tenth
• 60.98 to the nearest one

Solution

• 1,729.63 rounded to the nearest ten is 1,730.
• 1.0144 rounded to the nearest tenth is 1.0.
• 60.98 rounded to the nearest one is 61.

Sometimes we hear a phrase such as "round to the fourth decimal place" or "round to three decimal places." This phrase means that the round-off digit is the fourth decimal digit (7the digit in the ten-thousandths position) or third decimal digit (the digit in the thousandths position), respectively.

Example \(\PageIndex{1}\)

Round each of the following numbers.

• 67.129 to the second decimal place
• 67.129558 to 3 decimal places

Solution

• 67.129 rounded to the second decimal place is 67.13.
• 67.129558 rounded to 3 decimal places is 67.130.

Now, try these on your own.

Exercise \(\PageIndex{1}\)

Round each decimal to the specified position.

1. 4.816 to the nearest hundredth.
2. 0.35928 to the nearest ten thousandths.
3. 82.1 to the nearest one.
4. 753.98 to the hundreds place.
5. Round 43.99446 to three decimal places.
6. Round 105.019997 to four decimal places.
7. Round 99.9999 to the second decimal place.