3.2.1: Double Integrals Part 1 (Exercises)

In exercises 1 and 2, use the midpoint rule with \(m = 4\) and \(n = 2\) to estimate the volume of the solid bounded by the surface \(z = f(x,y)\), the vertical planes \(x = 1\), \(x = 2\), \(y = 1\), and \(y = 2\), and the horizontal plane \(z = 0\).

1) \(f(x,y) = 4x + 2y + 8xy\)

Answer

\(27\)

2) \(f(x,y) = 16x^2 + \frac{y}{2}\)

In exercises 3 and 4, estimate the volume of the solid under the surface \(z = f(x,y)\) and above the rectangular region \(R\) by using a Riemann sum with \(m = n = 2\) and the sample points to be the lower left corners of the sub-rectangles of the partition.

3) \(f(x,y) = \sin x - \cos y\), \(R = [0, \pi] \times [0, \pi]\)

Answer

\(0\)

4) \(f(x,y) = \cos x + \cos y\), \(R = [0, \pi] \times [0, \frac{\pi}{2}]\)

5) Use the midpoint rule with \(m = n = 2\) to estimate \(\iint_R f(x,y) \,dA\), where the values of the function f on \(R = [8,10] \times [9,11]\) are given in the following table.

	\(y\)
\(x\)	9	9.5	10	10.5	11
8	9.8	5	6.7	5	5.6
8.5	9.4	4.5	8	5.4	3.4
9	8.7	4.6	6	5.5	3.4
9.5	6.7	6	4.5	5.4	6.7
10	6.8	6.4	5.5	5.7	6.8

Answer

\(21.3\)

6) The values of the function \(f\) on the rectangle \(R = [0,2] \times [7,9]\) are given in the following table. Estimate the double integral \(\iint_R f(x,y)\,dA\) by using a Riemann sum with \(m = n = 2\). Select the sample points to be the upper right corners of the sub-squares of R.

	\(y_0 = 7\)	\(y_1 = 8\)	\(y_2 = 9\)
\(x_0 = 0\)	10.22	10.21	9.85
\(x_1 = 1\)	6.73	9.75	9.63
\(x_2 = 2\)	5.62	7.83	8.21

7) The depth of a children’s 4-ft by 4-ft swimming pool, measured at 1-ft intervals, is given in the following table.

1. Estimate the volume of water in the swimming pool by using a Riemann sum with \(m = n = 2\). Select the sample points using the midpoint rule on \(R = [0,4] \times [0,4]\).
2. Find the average depth of the swimming pool.

   	\(y\)
   \(x\)	0	1	2	3	4
   0	1	1.5	2	2.5	3
   1	1	1.5	2	2.5	3
   2	1	1.5	1.5	2.5	3
   3	1	1	1.5	2	2.5
   4	1	1	1	1.5	2

Answer

a. 28 \(\text{ft}^3\)
b. 1.75 ft.

8) The depth of a 3-ft by 3-ft hole in the ground, measured at 1-ft intervals, is given in the following table.

1. Estimate the volume of the hole by using a Riemann sum with \(m = n = 3\) and the sample points to be the upper left corners of the sub-squares of \(R\).
2. Find the average depth of the hole.

   	\(y\)
   \(x\)	0	1	2	3
   0	6	6.5	6.4	6
   1	6.5	7	7.5	6.5
   2	6.5	6.7	6.5	6
   3	6	6.5	5	5.6

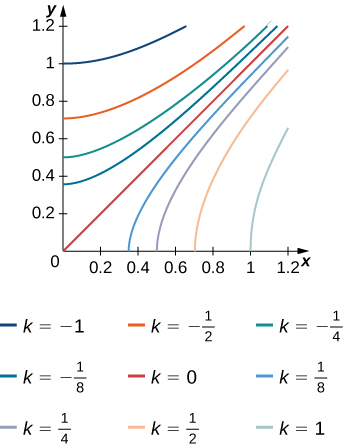
9) The level curves \(f(x,y) = k\) of the function \(f\) are given in the following graph, where \(k\) is a constant.

1. Apply the midpoint rule with \(m = n = 2\) to estimate the double integral \(\iint_R f(x,y)\,dA\), where \(R = [0.2,1] \times [0,0.8]\).
2. Estimate the average value of the function \(f\) on \(R\).

   

Answer

a. Answers will vary somewhat, but should be close to these: \(f(0.4,0.2) \approx 0.125\), \(f(0.4,0.6) \approx− 0.2\), \(f(0.8,0.2) \approx 0.6\), and \(f(0.8,0.6) \approx 0.3\).
Since the area of each rectangle is \(\Delta A_i = (0.4)(0.4) = 0.16 \text{ units}^2\), \(\displaystyle \iint_R f(x,y)\,dA = \int_{0.2}^{1}\int_{0}^{0.8} f(x,y) \,dy\,dx \approx f(0.4,0.2)(0.16)+f(0.4,0.6)(0.16) +f(0.8,0.2) (0.16) + f(0.8,0.6)(0.16) = 0.132\)
b. \(f_{ave} = \dfrac{\int_{0.2}^{1}\int_{0}^{0.8} f(x,y) \,dy\,dx}{\text{area of }R}\approx \dfrac{\int_{0.2}^{1}\int_{0}^{0.8} f(x,y) \,dy\,dx}{0.64} \approx 0.206\)

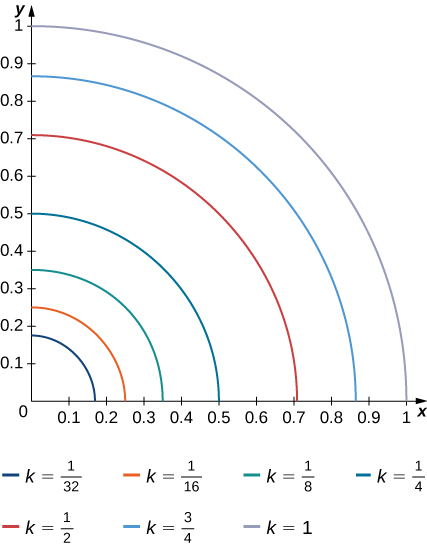
10) The level curves \(f(x,y) = k\) of the function \(f\) are given in the following graph, where \(k\) is a constant.

1. Apply the midpoint rule with \(m = n = 2\) to estimate the double integral \(\iint_R f(x,y)\,dA\), where \(R = [0.1,0.5] \times [0.1,0.5]\).
2. Estimate the average value of the function f on \(R\).

   

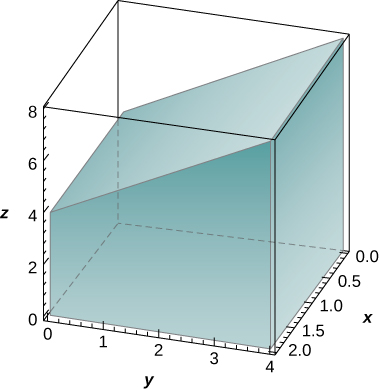
11) The solid lying under the surface \(z = \sqrt{4 - y^2}\) and above the rectangular region\( R = [0,2] \times [0,2]\) is illustrated in the following graph. Evaluate the double integral \(\iint_Rf(x,y)\), where \(f(x,y) = \sqrt{4 - y^2}\) by finding the volume of the corresponding solid.

Answer

\(2\pi\)

12) The solid lying under the plane \(z = y + 4\) and above the rectangular region \(R = [0,2] \times [0,4]\) is illustrated in the following graph. Evaluate the double integral \(\iint_R f(x,y)\,dA\), where \(f(x,y) = y + 4\), by finding the volume of the corresponding solid.

In the exercises 13 - 20, calculate the integrals by reversing the order of integration.

13) \(\displaystyle \int_{-1}^1\left(\int_{-2}^2 (2x + 3y + 5)\,dx \right) \space dy\)

Answer

\(40\)

14) \(\displaystyle \int_0^2\left(\int_0^1 (x + 2e^y + 3)\,dx \right) \space dy\)

15) \(\displaystyle \int_1^{27}\left(\int_1^2 (\sqrt[3]{x} + \sqrt[3]{y})\,dy \right) \space dx\)

Answer

\(\frac{81}{2} + 39\sqrt[3]{2}\)

16) \(\displaystyle \int_1^{16}\left(\int_1^8 (\sqrt[4]{x} + 2\sqrt[3]{y})\,dy \right) \space dx\)

17) \(\displaystyle \int_{\ln 2}^{\ln 3}\left(\int_0^1 e^{x+y}\,dy \right) \space dx\)

Answer

\(e - 1\)

18) \(\displaystyle \int_0^2\left(\int_0^1 3^{x+y}\,dy \right) \space dx\)

19) \(\displaystyle \int_1^6\left(\int_2^9 \frac{\sqrt{y}}{x^2}\,dy \right) \space dx\)

Answer

\(15 - \frac{10\sqrt{2}}{9}\)

20) \(\displaystyle \int_1^9 \left(\int_4^2 \frac{\sqrt{x}}{y^2}\,dy \right)\,dx\)

In exercises 21 - 34, evaluate the iterated integrals by choosing the order of integration.

21) \(\displaystyle \int_0^{\pi} \int_0^{\pi/2} \sin(2x)\cos(3y)\,dx \space dy\)

Answer

\(0\)

22) \(\displaystyle \int_{\pi/12}^{\pi/8}\int_{\pi/4}^{\pi/3} [\cot x + \tan(2y)]\,dx \space dy\)

23) \(\displaystyle \int_1^e \int_1^e \left[\frac{1}{x}\sin(\ln x) + \frac{1}{y}\cos (\ln y)\right] \,dx \space dy\)

Answer

\((e − 1)(1 + \sin 1 − \cos 1)\)

24) \(\displaystyle \int_1^e \int_1^e \frac{\sin(\ln x)\cos (\ln y)}{xy} \,dx \space dy\)

25) \(\displaystyle \int_1^2 \int_1^2 \left(\frac{\ln y}{x} + \frac{x}{2y + 1}\right)\,dy \space dx\)

Answer

\(\frac{3}{4}\ln \left(\frac{5}{3}\right) + 2 (\ln 2)^2 - \ln 2\)

26) \(\displaystyle \int_1^e \int_1^2 x^2 \ln(x)\,dy \space dx\)

27) \(\displaystyle \int_1^{\sqrt{3}} \int_1^2 y \space \arctan \left(\frac{1}{x}\right) \,dy \space dx\)

Answer

\(\frac{1}{8}[(2\sqrt{3} - 3) \pi + 6 \space \ln 2]\)

28) \(\displaystyle \int_0^1 \int_0^{1/2} (\arcsin x + \arcsin y)\,dy \space dx\)

29) \(\displaystyle \int_0^1 \int_1^2 xe^{x+4y}\,dy \space dx\)

Answer

\(\frac{1}{4}e^4 (e^4 - 1)\)

30) \(\displaystyle \int_1^2 \int_0^1 xe^{x-y}\,dy \space dx\)

31) \(\displaystyle \int_1^e \int_1^e \left(\frac{\ln y}{\sqrt{y}} + \frac{\ln x}{\sqrt{x}}\right)\,dy \space dx\)

Answer

\(4(e - 1)(2 - \sqrt{e})\)

32) \(\displaystyle \int_1^e \int_1^e \left(\frac{x \space \ln y}{\sqrt{y}} + \frac{y \space \ln x}{\sqrt{x}}\right)\,dy \space dx\)

33) \(\displaystyle \int_0^1 \int_1^2 \left(\frac{x}{x^2 + y^2} \right)\,dy \space dx\)

Answer

\(-\frac{\pi}{4} + \ln \left(\frac{5}{4}\right) - \frac{1}{2} \ln 2 + \arctan 2\)

34) \(\displaystyle \int_0^1 \int_1^2 \frac{y}{x + y^2}\,dy \space dx\)

In exercises 35 - 38, find the average value of the function over the given rectangles.

35)\(f(x,y) = −x +2y\), \(R = [0,1] \times [0,1]\)

Answer

\(\frac{1}{2}\)

36) \(f(x,y) = x^4 + 2y^3\), \(R = [1,2] \times [2,3]\)

37) \(f(x,y) = \sinh x + \sinh y\), \(R = [0,1] \times [0,2]\)

Answer

\(\frac{1}{2}(2 \space \cosh 1 + \cosh 2 - 3)\).

38) \(f(x,y) = \arctan(xy)\), \(R = [0,1] \times [0,1]\)

39) Let \(f\) and \(g\) be two continuous functions such that \(0 \leq m_1 \leq f(x) \leq M_1\) for any \(x ∈ [a,b]\) and \(0 \leq m_2 \leq g(y) \leq M_2\) for any\( y ∈ [c,d]\). Show that the following inequality is true:

\[m_1m_2(b-a)(c-d) \leq \int_a^b \int_c^d f(x) g(y)\,dy dx \leq M_1M_2 (b-a)(c-d). \nonumber \]

In exercises 40 - 43, use property v. of double integrals and the answer from the preceding exercise to show that the following inequalities are true.

40) \(\frac{1}{e^2} \leq \iint_R e^{-x^2 - y^2} \space dA \leq 1\), where \(R = [0,1] \times [0,1]\)

41) \(\frac{\pi^2}{144} \leq \iint_R \sin x \cos y \space dA \leq \frac{\pi^2}{48}\), where \(R = \left[ \frac{\pi}{6}, \frac{\pi}{3}\right] \times \left[ \frac{\pi}{6}, \frac{\pi}{3}\right]\)

42) \(0 \leq \iint_R e^{-y}\space \cos x \space dA \leq \frac{\pi}{2}\), where \(R = \left[0, \frac{\pi}{2}\right] \times \left[0, \frac{\pi}{2}\right]\)

43) \(0 \leq \iint_R (\ln x)(\ln y) \,dA \leq (e - 1)^2\), where \(R = [1, e] \times [1, e] \)

44) Let \(f\) and \(g\) be two continuous functions such that \(0 \leq m_1 \leq f(x) \leq M_1\) for any \(x ∈ [a,b]\) and \(0 \leq m_2 \leq g(y) \leq M_2\) for any \(y ∈ [c,d]\). Show that the following inequality is true:

\[(m_1 + m_2) (b - a)(c - d) \leq \int_a^b \int_c^d |f(x) + g(y)| \space dy \space dx \leq (M_1 + M_2)(b - a)(c - d) \nonumber \]

In exercises 45 - 48, use property v. of double integrals and the answer from the preceding exercise to show that the following inequalities are true.

45) \(\frac{2}{e} \leq \iint_R (e^{-x^2} + e^{-y^2}) \,dA \leq 2\), where \(R = [0,1] \times [0,1]\)

46) \(\frac{\pi^2}{36}\iint_R (\sin x + \cos y)\,dA \leq \frac{\pi^2 \sqrt{3}}{36}\), where \(R = [\frac{\pi}{6}, \frac{\pi}{3}] \times [\frac{\pi}{6}, \frac{\pi}{3}]\)

47) \(\frac{\pi}{2}e^{-\pi/2} \leq \iint_R (\cos x + e^{-y})\,dA \leq \pi\), where \(R = [0, \frac{\pi}{2}] \times [0, \frac{\pi}{2}]\)

48) \(\frac{1}{e} \leq \iint_R (e^{-y} - \ln x) \,dA \leq 2\), where \(R = [0, 1] \times [0, 1]\)

In exercises 49 - 50, the function \(f\) is given in terms of double integrals.

1. Determine the explicit form of the function \(f\).
2. Find the volume of the solid under the surface \(z = f(x,y)\) and above the region \(R\).
3. Find the average value of the function \(f\) on \(R\).
4. Use a computer algebra system (CAS) to plot \(z = f(x,y)\) and \(z = f_{ave}\) in the same system of coordinates.

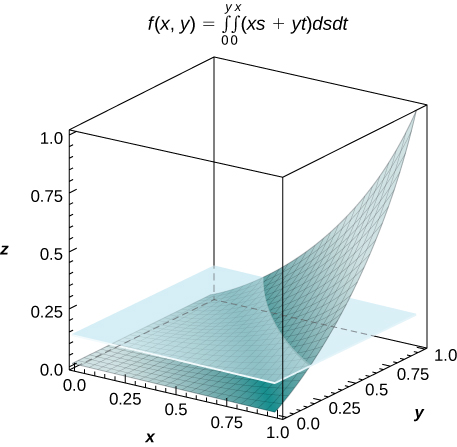
49) [T] \(f(x,y) = \int_0^y \int_0^x (xs + yt) ds \space dt\), where \((x,y) \in R = [0,1] \times [0,1]\)

Answer

a. \(f(x,y) = \frac{1}{2} xy (x^2 + y^2)\);
b. \(V = \int_0^1 \int_0^1 f(x,y)\,dx \space dy = \frac{1}{8}\);
c. \(f_{ave} = \frac{1}{8}\);

d.

50) [T] \(f(x,y) = \int_0^x \int_0^y [\cos(s) + \cos(t)] \, dt \space ds\), where \((x,y) \in R = [0,3] \times [0,3]\)

51) Show that if \(f\) and \(g\) are continuous on \([a,b]\) and \([c,d]\), respectively, then

\(\displaystyle \int_a^b \int_c^d |f(x) + g(y)| dy \space dx = (d - c) \int_a^b f(x)\,dx\)

\(\displaystyle + \int_a^b \int_c^d g(y)\,dy \space dx = (b - a) \int_c^d g(y)\,dy + \int_c^d \int_a^b f(x)\,dx \space dy\).

52) Show that \(\displaystyle \int_a^b \int_c^d yf(x) + xg(y)\,dy \space dx = \frac{1}{2} (d^2 - c^2) \left(\int_a^b f(x)\,dx\right) + \frac{1}{2} (b^2 - a^2) \left(\int_c^d g(y)\,dy\right)\).

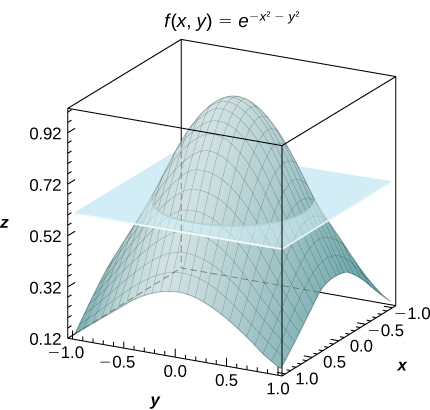
53) [T] Consider the function \(f(x,y) = e^{-x^2-y^2}\), where \((x,y) \in R = [−1,1] \times [−1,1]\).

1. Use the midpoint rule with \(m = n = 2,4,..., 10\) to estimate the double integral \(I = \iint_R e^{-x^2 - y^2} dA\). Round your answers to the nearest hundredths.
2. For \(m = n = 2\), find the average value of f over the region R. Round your answer to the nearest hundredths.
3. Use a CAS to graph in the same coordinate system the solid whose volume is given by \(\iint_R e^{-x^2-y^2} dA\) and the plane \(z = f_{ave}\).

Answer

a. For \(m = n = 2\), \(I = 4e^{-0.5} \approx 2.43\)
b. \(f_{ave} = e^{-0.5} \simeq 0.61\);

c.

54) [T] Consider the function \(f(x,y) = \sin (x^2) \space \cos (y^2)\), where \((x,y \in R = [−1,1] \times [−1,1]\).

1. Use the midpoint rule with \(m = n = 2,4,..., 10\) to estimate the double integral \(I = \iint_R \sin (x^2) \cos (y^2) \space dA\). Round your answers to the nearest hundredths.
2. For \(m = n = 2\), find the average value of \(f\)over the region R. Round your answer to the nearest hundredths.
3. Use a CAS to graph in the same coordinate system the solid whose volume is given by \(\iint_R \sin(x^2) \cos(y^2) \space dA\) and the plane \(z = f_{ave}\).

In exercises 55 - 56, the functions \(f_n\) are given, where \(n \geq 1\) is a natural number.

1. Find the volume of the solids \(S_n\) under the surfaces \(z = f_n(x,y)\) and above the region \(R\).
2. Determine the limit of the volumes of the solids \(S_n\) as \(n\) increases without bound.

55) \(f(x,y) = x^n + y^n + xy, \space (x,y) \in R = [0,1] \times [0,1]\)

Answer

a. \(\frac{2}{n + 1} + \frac{1}{4}\)
b. \(\frac{1}{4}\)

56) \(f(x,y) = \frac{1}{x^n} + \frac{1}{y^n}, \space (x,y) \in R = [1,2] \times [1,2]\)

57) Show that the average value of a function \(f\) on a rectangular region \(R = [a,b] \times [c,d]\) is \(f_{ave} \approx \frac{1}{mn} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}^*,y_{ij}^*)\),where \((x_{ij}^*,y_{ij}^*)\) are the sample points of the partition of \(R\), where \(1 \leq i \leq m\) and \(1 \leq j \leq n\).

58) Use the midpoint rule with \(m = n\) to show that the average value of a function \(f\) on a rectangular region \(R = [a,b] \times [c,d]\) is approximated by

\[f_{ave} \approx \frac{1}{n^2} \sum_{i,j =1}^n f \left(\frac{1}{2} (x_{i=1} + x_i), \space \frac{1}{2} (y_{j=1} + y_j)\right). \nonumber \]

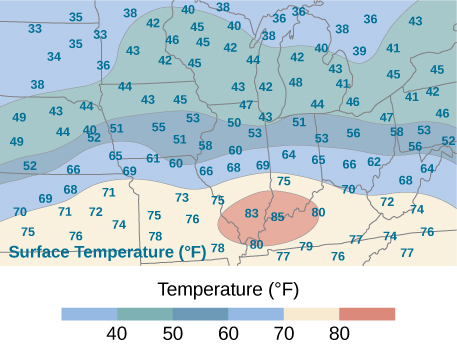
59) An isotherm map is a chart connecting points having the same temperature at a given time for a given period of time. Use the preceding exercise and apply the midpoint rule with \(m = n = 2\) to find the average temperature over the region given in the following figure.

Answer

\(56.5^{\circ}\) F; here \(f(x_1^*,y_1^*) = 71, \space f(x_2^*, y_1^*) = 72, \space f(x_2^*,y_1^*) = 40, \space f(x_2^*,y_2^*) = 43\), where \(x_i^*\) and \(y_j^*\) are the midpoints of the subintervals of the partitions of \([a,b]\) and \([c,d]\), respectively.