4.1E: Exercises for Section 12.1
- Last updated
- Dec 18, 2020
- Save as PDF
- Page ID
- 54101
( \newcommand{\kernel}{\mathrm{null}\,}\)
Introduction to Vector-Valued Functions
1) Give the component functions x=f(t) and y=g(t) for the vector-valued function ⇀r(t)=3sectˆi+2tantˆj.
- Answer
- Here we can say that f(t)=3sect,g(t)=2tant
so we have x(t)=3sect,y(t)=2tant.
2) Given ⇀r(t)=3sectˆi+2tantˆj, find the following values (if possible).
- ⇀r(π4)
- ⇀r(π)
- ⇀r(π2)
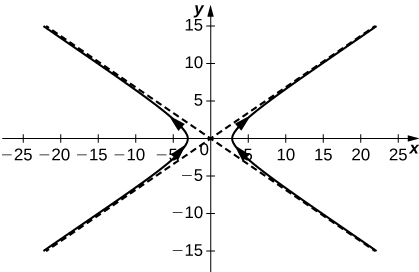
3) Sketch the curve of the vector-valued function ⇀r(t)=3sectˆi+2tantˆj and give the orientation of the curve. Sketch asymptotes as a guide to the graph.
- Answer
Limits of Vector-Valued Functions
4) Evaluate limt→0(etˆi+sinttˆj+e−tˆk)
5) Given the vector-valued function ⇀r(t)=⟨cost,sint⟩ find the following values:
- limt→π4⇀r(t)
- ⇀r(π3)
- Is ⇀r(t) continuous at t=π3?
- Graph ⇀r(t).
- Answer
-
a. ⟨√22,√22⟩,
b. ⟨12,√32⟩,
c. Yes, the limit as t approaches π3 is equal to r(π3),
d.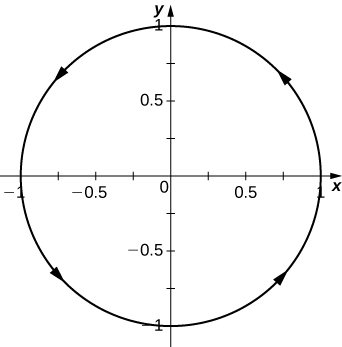
6) Given the vector-valued function ⇀r(t)=⟨t,t2+1⟩, find the following values:
- limt→−3⇀r(t)
- ⇀r(−3)
- Is ⇀r(t) continuous at x=−3?
- ⇀r(t+2)−⇀r(t)
7) Let ⇀r(t)=etˆi+sintˆj+lntˆk. Find the following values:
- ⇀r(π4)
- limt→π4⇀r(t)
- Is ⇀r(t) continuous at t=π4?
- Answer
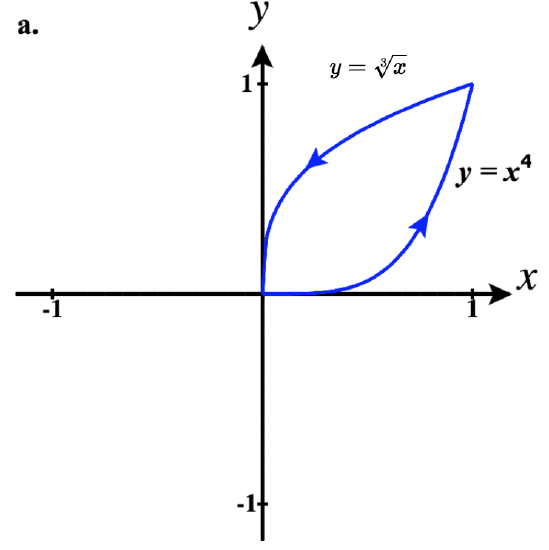
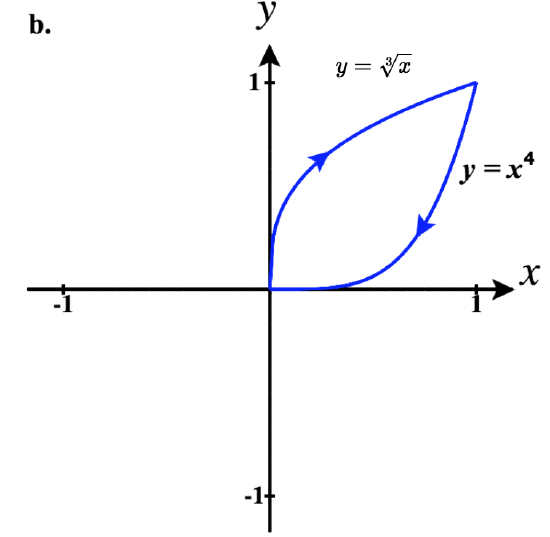
- a. ⟨eπ4,√22,ln(π4)⟩;
b. ⟨eπ4,√22,ln(π4)⟩;
c. Yes
For exercises 8 - 13, find the limit of the following vector-valued functions at the indicated value of t.
8) limt→4⟨√t−3,√t−2t−4,tan(πt)⟩
9) limt→π2⇀r(t) for ⇀r(t)=etˆi+sintˆj+lntˆk
- Answer
- ⟨eπ2,1,ln(π2)⟩
10) limt→∞⟨e−2t,2t+33t−1,arctan(2t)⟩
11) limt→e2⟨tln(t),lntt2,√ln(t2)⟩
- Answer
- 2e2ˆi+2e4ˆj+2ˆk
12) limt→π6⟨cos2t,sin2t,1⟩
13) limt→∞⇀r(t) for ⇀r(t)=2e−ti+e−tˆj+ln(t−1)ˆk
- Answer
- The limit does not exist because the limit of ln(t−1) as t approaches infinity does not exist.
Domain of a Vector-Valued Function
For problems 14 - 17, find the domain of the vector-valued functions.
14) Domain: ⇀r(t)=⟨t2,t,sint⟩
15) Domain: ⇀r(t)=⟨t2,tant,lnt⟩
- Answer
- D⇀r={t|t>0,t≠(2k+1)π2,wherekis any integer}
16) Domain: ⇀r(t)=⟨t2,√t−3,32t+1⟩
17) Domain: ⇀r(t)=⟨csc(t),1√t−3,ln(t−2)⟩
- Answer
- D⇀r={t|t>3,t≠nπ,wherenis any integer}
18) a. Find the domain of ⇀r(t)=2e−tˆi+e−tˆj+ln(t−1)ˆk.
b. For what values of t is ⇀r(t)=2e−tˆi+e−tˆj+ln(t−1)ˆk continuous?
- Answer
- a. D⇀r:(1,∞)
b. All t such that t∈(1,∞)
19) Domain: ⇀r(t)=(arccost)ˆi+√2t−1ˆj+ln(t)ˆk
- Answer
- D⇀r:[12,1]
Visualizing Vector-Valued Functions
20) Describe the curve defined by the vector-valued function ⇀r(t)=(1+t)ˆi+(2+5t)ˆj+(−1+6t)ˆk.
21) Let ⇀r(t)=⟨cost,t,sint⟩ and use it to answer the following questions.
- For what values of t is ⇀r(t) continuous?
- Sketch the graph of ⇀r(t).
- Answer
- a. ⇀r is continuous for all real numbers, i.e., for t∈R.
b. Note that there should be a z on the vertical axis in the cross-section in image (a) below instead of the y.
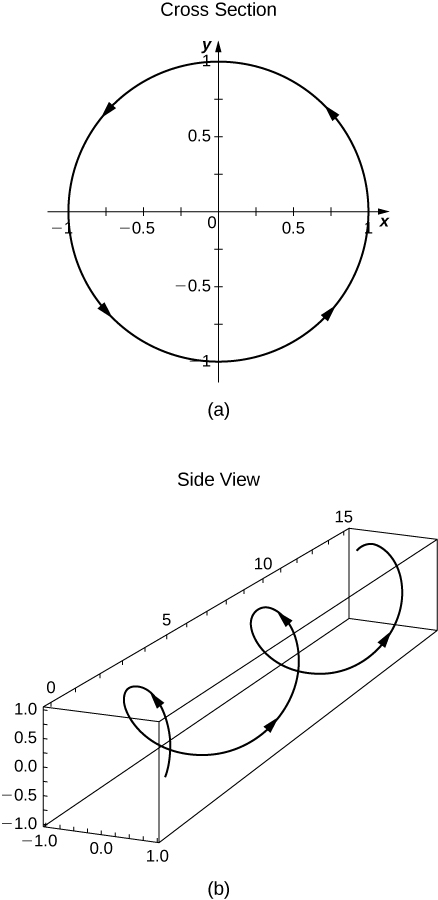
22) Produce a careful sketch of the graph of ⇀r(t)=t2ˆi+tˆj.
In questions 23 - 25, use a graphing utility to sketch each of the vector-valued functions:
23) [T] ⇀r(t)=2cos2tˆi+(2−√t)ˆj
- Answer
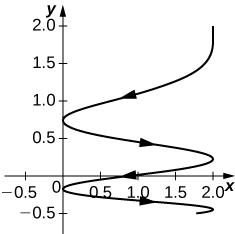
24) [T] ⇀r(t)=⟨ecos(3t),e−sin(t)⟩
25) [T] ⇀r(t)=⟨2−sin(2t),3+2cost⟩
- Answer
Finding Equations in x and y for the Path Traced out by Vector-Valued Functions
For questions 26-33, eliminate the parameter t, write the equation in Cartesian coordinates, then sketch the graph of the vector-valued functions.
26) ⇀r(t)=2tˆi+t2ˆj
(Hint: Let x=2t and y=t2. Solve the first equation for t in terms of x and substitute this result into the second equation.)
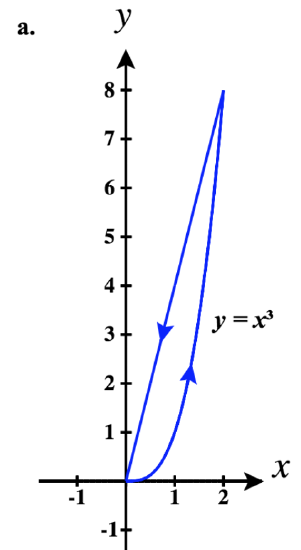
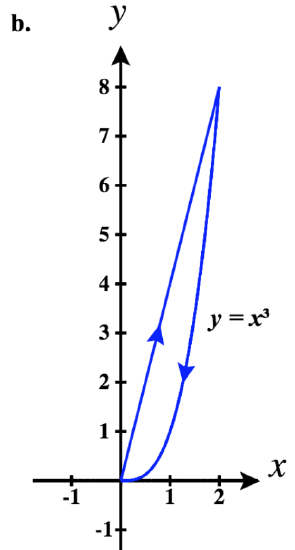
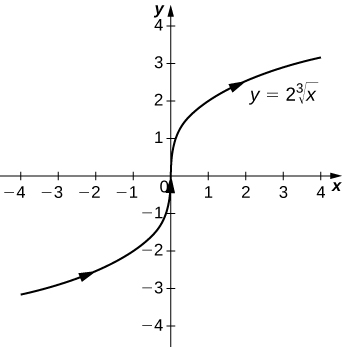
27) ⇀r(t)=t3ˆi+2tˆj
- Answer
-
y=23√x, a variation of the cube-root function
28) ⇀r(t)=sintˆi+costˆj
29) ⇀r(t)=3costˆi+3sintˆj
- Answer
-
x2+y2=9, a circle centered at (0,0) with radius 3, and a counterclockwise orientation

30) ⇀r(t)=⟨sint,4cost⟩
31) ⇀r(t)=2sintˆi−3costˆj
- Answer
-
x24+y29=1, an ellipse centered at (0,0) with intercepts at x=±2 and y=±3, and a clockwise orientation
32) ⇀r(t)=tantˆi−2sectˆj
33) ⇀r(t)=3sectˆi+4tantˆj
- Answer
-
x29−y216=1, a hyperbola centered at (0,0) with x-intercepts (3,0) and (−3,0), with orientation shown
Finding a Vector-Valued Function to Trace out the Graph of an Equation in x and y
For questions 34 - 40, find a vector-valued function that traces out the given curve in the indicated direction.
34) 4x2+9y2=36; clockwise and counterclockwise
35) y=x2; from left to right
- Answer
- ⇀r(t)=⟨t,t2⟩, where t increases
36) The line through P and Q where P is (1,4,−2) and Q is (3,9,6)
37) The circle, x2+y2=36, oriented clockwise, with position (−6,0) at time t=0.
- Answer
- ⇀r(t)=−6costˆi+6sintˆj
38) The ellipse, x2+y236=1, oriented counterclockwise
- Answer
- ⇀r(t)=costˆi+6sintˆj
39) The hyperbola, y236−x2=1, top piece is oriented from left-to-right
- Answer
- ⇀r(t)=tantˆi+6sectˆj
40) The hyperbola, x249−y264=1, right piece is oriented from bottom-to-top
- Answer
- ⇀r(t)=7sectˆi+8tantˆj
Parameterizing a Piecewise Path
For questions 41 - 44, provide a parameterization for each piecewise path. Try to write a parameterization that starts with t=0 and progresses on through values of t as you move from one piece to another.
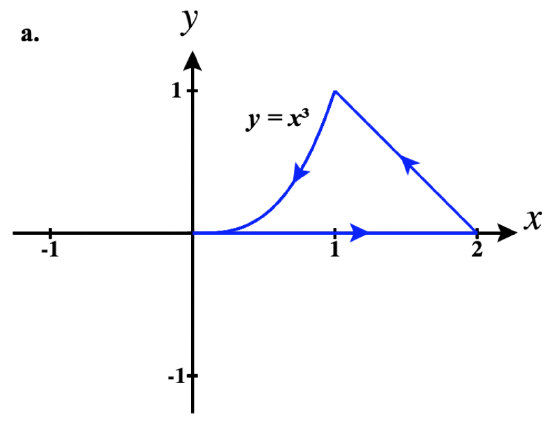
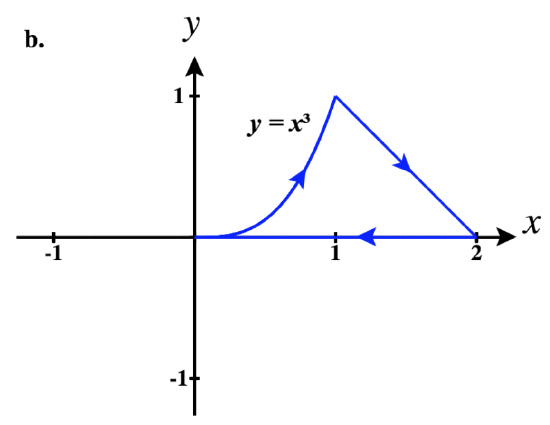
41)
- Answer
- a. ⇀r1(t)=tˆi+t4ˆj for 0≤t≤1
⇀r2(t)=−tˆi+3√−tˆj for −1≤t≤0
So a piecewise parameterization of this path is:
⇀r(t)={tˆi+t4ˆj,0≤t≤1(2−t)ˆi+3√2−tˆj,1<t≤2
b. ⇀r1(t)=tˆi+3√tˆj for 0≤t≤1
⇀r2(t)=−tˆi+(−t)4ˆj for −1≤t≤0
So a piecewise parameterization of this path is:
⇀r(t)={tˆi+3√tˆj,0≤t≤1(2−t)ˆi+(2−t)4ˆj,1<t≤2
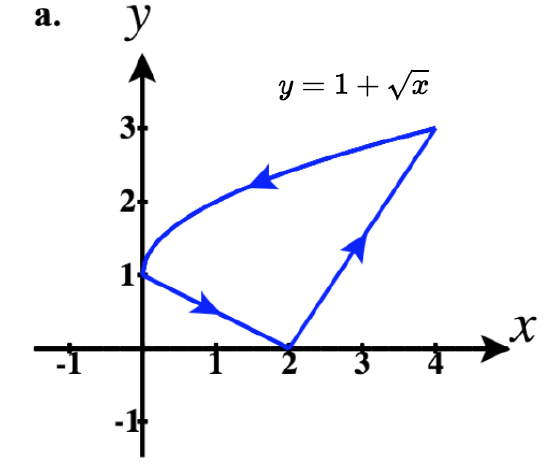
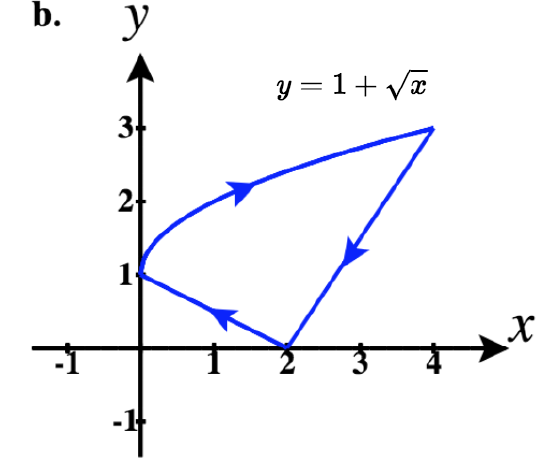
42)
43)
- Answer
- a. ⇀r1(t)=tˆi+0ˆj for 0≤t≤2
⇀r2(t)=−tˆi+(2+t)ˆj for −2≤t≤−1
⇀r3(t)=−tˆi+(−t)3ˆj for −1≤t≤0
So a piecewise parameterization of this path is:
⇀r(t)={tˆi,0≤t≤2(4−t)ˆi+(t−2)ˆj,2<t≤3(4−t)ˆi+(4−t)3ˆj,3<t≤4
b. ⇀r1(t)=tˆi+t3ˆj for 0≤t≤1
⇀r2(t)=tˆi+(2−t)ˆj for 1≤t≤2
⇀r3(t)=−tˆi+0ˆj for −2≤t≤0
So a piecewise parameterization of this path is:
⇀r(t)={tˆi+t3ˆj,0≤t≤1tˆi+(2−t)ˆj,1<t≤2(4−t)ˆi,2<t≤4
44)
Additional Vector-Valued Function Questions
For questions 45 - 48, consider the curve described by the vector-valued function ⇀r(t)=(50e−tcost)ˆi+(50e−tsint)ˆj+(5−5e−t)ˆk.
45) What is the initial point of the path corresponding to ⇀r(0)?
- Answer
- (50,0,0)
46) What is limt→∞⇀r(t)?
47) [T] Use technology to sketch the curve.
- Answer
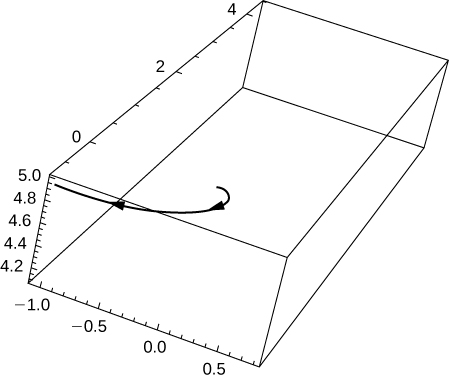
48) Eliminate the parameter t to show that z=5−r10 where r2=x2+y2.
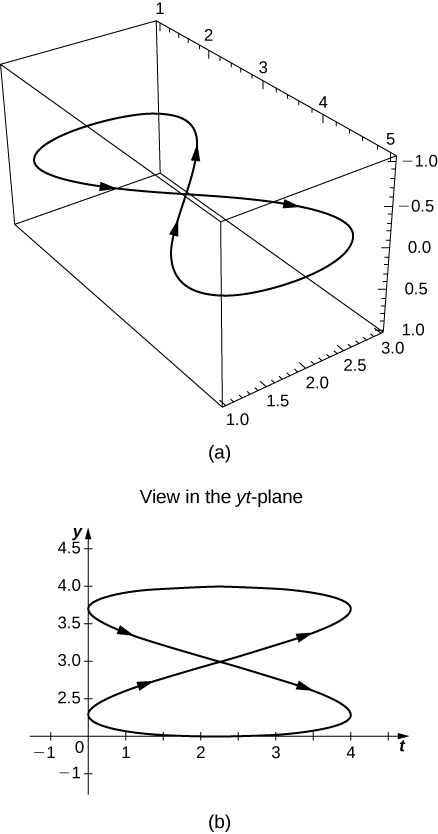
49) [T] Let ⇀r(t)=costˆi+sintˆj+0.3sin(2t)ˆk. Use technology to graph the curve (called the roller-coaster curve) over the interval [0,2π). Choose at least two views to determine the peaks and valleys.
- Answer
50) [T] Use the result of the preceding problem to construct an equation of a roller coaster with a steep drop from the peak and steep incline from the “valley.” Then, use technology to graph the equation.
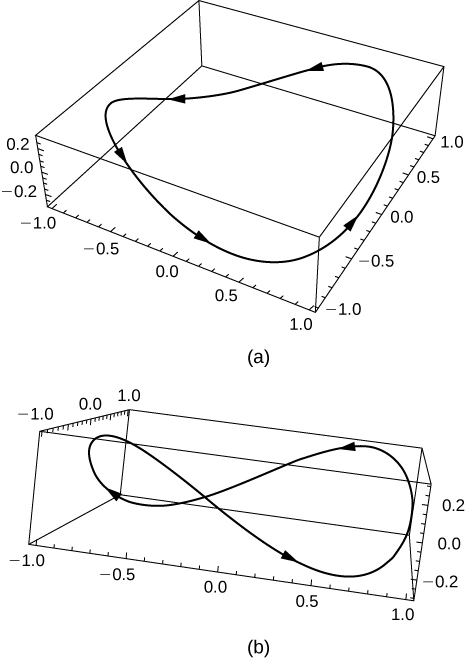
51) Use the results of the preceding two problems to construct an equation of a path of a roller coaster with more than two turning points (peaks and valleys).
- Answer
-
One possibility is ⇀r(t)=costˆi+sintˆj+sin(4t)ˆk. By increasing the coefficient of t in the third component, the number of turning points will increase.
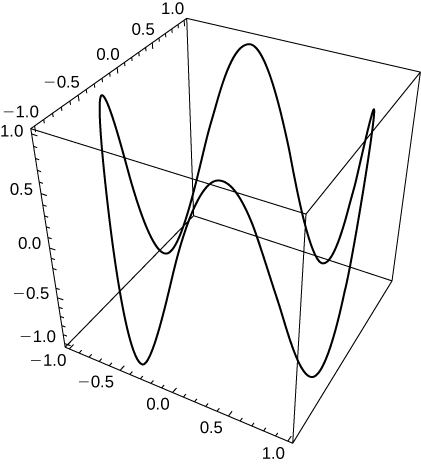
52) Complete the following investigation.
- Graph the curve ⇀r(t)=(4+cos(18t))cos(t)ˆi+(4+cos(18t)sin(t))ˆj+0.3sin(18t)ˆk using two viewing angles of your choice to see the overall shape of the curve.
- Does the curve resemble a “slinky”?
- What changes to the equation should be made to increase the number of coils of the slinky?
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Paul Seeburger (Monroe Community College) created problems 12, 14, 19, 22, 30-33, 37- 44.