2.9: Applied Optimization
- Last updated
- Save as PDF
- Page ID
- 80892
We have used derivatives to help find the maximums and minimums of some functions given by equations, but it is very unlikely that someone will simply hand you a function and ask you to find its extreme values. More typically, someone will describe a problem and ask your help in maximizing or minimizing something: What is the largest volume package which the post office will take?
; What is the quickest way to get from here to there?
; or What is the least expensive way to accomplish some task?
In this section, we’ll discuss how to find these extreme values using calculus.
Max/Min Applications
Example
The manager of a garden store wants to build a 600 square foot rectangular enclosure on the store’s parking lot in order to display some equipment. Three sides of the enclosure will be built of redwood fencing, at a cost of $7 per running foot. The fourth side will be built of cement blocks, at a cost of $14 per running foot. Find the dimensions of the least costly such enclosure.
The process of finding maxima or minima is called optimization. The function we're optimizing is called the objective function (or objective equation). The objective function can be recognized by its proximity to est
words (greatest, least, highest, farthest, most, …). Look at the garden store example; the cost function is the objective function.
In many cases, there are two (or more) variables in the problem. In the garden store example again, the length and width of the enclosure are both unknown. If there is an equation that relates the variables we can solve for one of them in terms of the others, and write the objective function as a function of just one variable. Equations that relate the variables in this way are called constraint equations. The constraint equations are always equations, so they will have equals signs. For the garden store, the fixed area relates the length and width of the enclosure. This will give us our constraint equation.
Max-Min Story Problem Technique
- Translate the English statement of the problem line by line into a picture (if that applies) and into math. This is often the hardest step!
- Identify the objective function. Look for words indicating a largest or smallest value.
- If you seem to have two or more variables, find the constraint equation. Think about the English meaning of the word
constraint
, and remember that the constraint equation will have an equals sign. - Solve the constraint equation for one variable and substitute into the objective function. Now you have an equation of one variable.
- If you seem to have two or more variables, find the constraint equation. Think about the English meaning of the word
- Use calculus to find the optimum values. (Take derivative, find critical points, test. Don't forget to check the endpoints!)
- Look back at the question to make sure you answered what was asked. Translate your number answer back into English.
Here is a link to the examples used in the videos in this section: Applied Optimization Examples.
Example \(\PageIndex{1}\)
The manager of a garden store wants to build a 600 square foot rectangular enclosure on the store's parking lot in order to display some equipment. Three sides of the enclosure will be built of redwood fencing, at a cost of $7 per running foot. The fourth side will be built of cement blocks, at a cost of $14 per running foot. Find the dimensions of the least costly such enclosure.
First, translate line by line into math and a picture:
| Text | Translation |
|
The manager of a garden store wants to build a 600 square foot rectangular enclosure on the store's parking lot in order to display some equipment. Three sides of the enclosure will be built of redwood fencing, at a cost of $7 per running foot. The fourth side will be built of cement blocks, at a cost of $14 per running foot. Find the dimensions of the least costly such enclosure. |
Let \(x\) and \(y\) be the dimensions of the enclosure, with \(y\) being the length of the side made of blocks. Then: \[\text{Area} = A = xy = 600.\nonumber \] \(2x + y\) costs $7 per foot, \(y\) costs $14 per foot, so \[\text{Cost} = C = 7(2x + y) + 14y = 14x + 21y.\nonumber \] Find \(x\) and \(y\) so that \(C\) is minimized. |
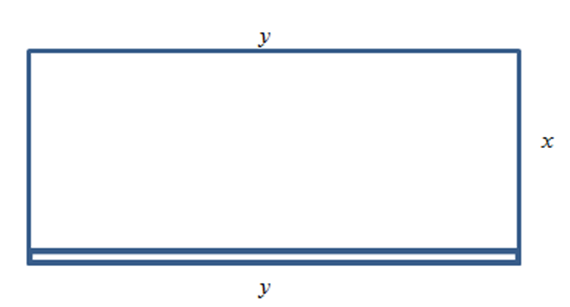
The objective function is the cost function, and we want to minimize it. As it stands, though, it has two variables, so we need to use the constraint equation. The constraint equation is the fixed area \(A = xy = 600\). Solve \(A\) for \(x\) to get \( x=\frac{600}{y} \), and then substitute into \(C\): \[C=14\left(\frac{600}{y}\right)+21y=\frac{8400}{y}+21y.\nonumber \]
Now we have a function of just one variable, so we can find the minimum using calculus.
\[C'=-\frac{8400}{y^2}+21\nonumber \] \(C'\) is undefined for \(y = 0\), and \(C' = 0\) when \(y = 20\) or \(y = -20\).
Of these three critical numbers, only \(y = 20\) makes sense (is in the domain of the actual function) – remember that \(y\) is a length, so it can’t be negative, and \(y = 0\) would mean there was no enclosure at all, so it couldn't have an area of 600 square feet.
Test \(y = 20\) (here we chose the second derivative test): \[C''=\frac{16800}{y^3} \gt 0,\nonumber \] so this is a local minimum.
Since this is the only critical point in the domain, this must be the global minimum. Going back to our constraint function, we can find that when \(y = 20\), \(x = 30\). The dimensions of the enclosure that minimize the cost are 20 feet by 30 feet.
When trying to maximize their revenue, businesses also face the constraint of consumer demand. While a business would love to see lots of products at a very high price, typically demand decreases as the price of goods increases. In simple cases, we can construct that demand curve to allow us to maximize revenue.
Example \(\PageIndex{2}\)
A concert promoter has found that if she sells tickets for $50 each, she can sell 1200 tickets, but for each $5 she raises the price, 50 less people attend. What price should she sell the tickets at to maximize her revenue?
We are trying to maximize revenue, and we know that \( R=pq \), where \(p\) is the price per ticket, and \(q\) is the quantity of tickets sold.
The problem provides information about the demand relationship between price and quantity – as price increases, demand decreases. We need to find a formula for this relationship. To investigate, let's calculate what will happen to attendance if we raise the price:
| Price, \( p \) | 50 | 55 | 60 | 65 |
| Quantity, \( q \) | 1200 | 1150 | 1100 | 1050 |
You might recognize this as a linear relationship. We can find the slope for the relationship by using two points: \[m=\frac{1150-1200}{55-50}=\frac{-50}{5}=-10.\nonumber \]
You may notice that the second step in that calculation corresponds directly to the statement of the problem: the attendance drops 50 people for every $5 the price increases.
Using the point-slope form of the line, we can write the equation relating price and quantity: \[q-1200=-10(p-50).\nonumber \]
Simplifying to slope-intercept form gives the demand equation \[ q=1700-10p. \nonumber \]
Substituting this into our revenue equation, we get an equation for revenue involving only one variable: \[R=pq=p(1700-10p)=1700p-10p^2.\nonumber \]
Now, we can find the maximum of this function by finding critical numbers. \( R'=1700-20p \), so \( R'=0 \) when \(p = 85\).
Using the second derivative test, \( R''=-20 \lt 0 \) (for any value of \( p \)), so the critical number is a local maximum. Since it is the only critical number, we can also conclude that it is the global maximum.
The promoter will be able to maximize revenue by charging $85 per ticket. At this price, she will sell \( q=1700-10(85)=850 \) tickets, generating $72,250 in revenue.
Marginal Revenue = Marginal Cost
You may have heard before that profit is maximized when marginal cost and marginal revenue are equal.
Now you can see why people say that! (Even though it’s not completely true.)
Example \(\PageIndex{3}\)
Suppose we want to maximize profit.
Now we know what to do – find the profit function, find its critical points, test them, etc.
But remember that Profit = Revenue - Cost. So Profit' = Revenue' - Cost'. That is, the derivative of the profit function is \(MR - MC\).
Now let’s find the critical points – those will be where Profit' = 0 or is undefined. Profit' = 0 when \(MR - MC = 0\), or where \(MR = MC\).
Profit has critical points when Marginal Revenue and Marginal Cost are equal.
In all the cases we'll see in this class, Profit will be very well behaved, and we won't have to worry about looking for critical points where Profit' is undefined. But remember that not all critical points are local max! The places where \(MR = MC\) could represent local max, local min, or neither one.
Example \(\PageIndex{4}\)
A company sells \(q\) ribbon winders per year at \(\$p\) per ribbon winder. The demand function for ribbon winders is given by: \(p=300-0.02q\). The ribbon winders cost $30 apiece to manufacture, plus there are fixed costs of $9000 per year. Find the quantity where profit is maximized.
We want to maximize profit, but there isn’t a formula for profit given. So let's make one. We can find a function for Revenue = \(pq\) using the demand function for \(p\). \[R(q)=(300-0.02q)q=300q-0.02q^2.\nonumber \]
We can also find a function for Cost, using the variable cost of $30 per ribbon winder, plus the fixed cost: \[C(q)=9000+30q.\nonumber \]
Putting them together, we get a function for Profit: \[P(q)=R(q)-C(q)=\left(300q-0.02q^2\right)-(9000+30q)=-0.02q^2+270q-9000\nonumber \]
Now we have two choices. We can find the critical points of Profit by taking the derivative of \(P(q)\) directly, or we can find \(MR\) and \(MC\) and set them equal. (Naturally, we'll get the same answer either way.)
Let's use \(MR = MC\) this time. \[ \begin{align*} MR & = 300-0.04q\\ MC & = 30\\ 300-0.04q & = 30\\ 270 & = 0.04q\\ q & = 6750 \end{align*} \nonumber \]
The only critical point is at \(q = 6750\). Now we need to be sure this is a local max and not a local min. In this case, we'll look to the graph of \(P(q)\) – it's a downward opening parabola, so this must be a local max. And since it's the only critical point, it must also be the global max.
Profit is maximized when they sell 6750 ribbon winders.
Average Cost = Marginal Cost
Average cost is minimized when average cost = marginal cost
is another saying that isn’t quite true; in this case, the correct statement is:
Average Cost has critical points when Average Cost and Marginal Cost are equal.
Let’s look at a geometric argument here. Remember that the average cost is the slope of the diagonal line, the line from the origin to the point on the total cost curve. If you move your clear plastic ruler around, you’ll see (and feel) that the slope of the diagonal line is smallest when the diagonal line just touches the cost curve – when the diagonal line is actually a tangent line – when the average cost is equal to the marginal cost.
Example \(\PageIndex{5}\)
The cost in dollars to produce \(q\) gift baskets is given by \(C(q) = 160+2q+ .1q^2\). Find the quantity where the average cost is minimum.
Solution
\(A(q) = \frac{C(q)}{q} = \frac{160}{q} + 2 + .1q\). We could find the critical points by finding \(A'\), or by setting average cost to marginal cost; we’ll do the latter this time.
\[MC(q) = 2+ .2q. \nonumber\]
So we want to solve:
\[\begin{align*} \frac{160}{q} +2+.1q &= 2+.2q \\ \frac{160}{q} &= .1q \\ 1600 &= q^2 \\ q&=40 \end{align*}\]
The critical point of average cost is when \(q = 40\).
Notice that we still have to confirm that the critical point is a minimum. For this, we can use the first or second derivative test on \(A(q)\).
\[\begin{align*} A'(q) = \frac{-160}{q^2} +.1 \\ A''(q) = \frac{320}{q^3} >0 \end{align*}\]
The second derivative is positive for all positive \(q\), so that means this is a local min. Average cost is minimized when they produce 40 gift baskets; at that quantity, the average cost is $10 per basket.


