4.E: Functions of Two Variables (Exercises)

4.1 Exercises

Exercise $\PageIndex{1}$

$F(x,y) = x^2-y^2$. Find

a) $F(0,4)$

b) $F(4,0)$

c) $F(x,4)$

d) $F(4,y)$

e) $F(800,800)$

f) $F(x,x)$

g) $F(x,-x)$

Exercise $\PageIndex{2}$

$g(s,t)=\sqrt{st^2}$. Find

a) $g(1,9)$

b) $g(9,1)$

c) $g(1,t)$

d) $g(s,9)$

e) $g(w,z+1)$

Exercise $\PageIndex{3}$

Let $f(x,y,z,w) = x^2 - \frac{1}{zw}+xyz^2$. Evaluate $f(1,2,3,4)$.

Exercise $\PageIndex{4}$

Let $f(x,y,z,w) = \sqrt{xy} - w^2 + 102yz$. Evaluate $f(1,2,3,4)$.

Exercise $\PageIndex{5}$

Here is a table showing the function $A(t,r)$

$\overset{t}{\downarrow} \ r\rightarrow$	.03	.04	.05	.06	.07
1	30.45	40.81	51.27	61.84	72.51
2	61.84	83.29	105.17	127.50	150.27
3	94.17	127.50	161.83	197.22	233.68

a) Find $A(2, .05)$

b) Find $A(.05, .2)$

c) Is $A(t, .06)$ an increasing or decreasing function of $t$?

d) Is $A(3, r)$ an increasing or decreasing function of $r$?

Exercise $\PageIndex{6}$

Here is a table showing values for the function $H(t,h)$.

$\overset{t}{\downarrow} \ h\rightarrow$	100	150	200
0	100	150	200
1	110.1	160.1	210.1
2	110.4	160.4	210.4
3	100.9	150.9	200.9
4	81.6	131.6	181.6
5	52.5	102.5	152.5

a) Is $H(t, 150)$ an increasing or decreasing function of $t$?

b) Is $H( 4, h)$ an increasing or decreasing function of $h$?

c) Fill in the blanks: The maximum value shown on this table is $H$(___,___) =____.

d) Fill in the blanks: The minimum value shown on this table is $H$(___,___) =____.

Exercise $\PageIndex{7}-\PageIndex{10}$

In problems 7 – 10, plot the given points.

7. $A = (0,3,4), B = (1,4,0), C = (1,3,4), D = (1, 4,2)$

8. $E = (4,3,0), F = (3,0,1), G = (0,4,1), H = (3,3,1)$

9. $P = (2,3,–4), Q = (1,–2,3), R = (4,–1,–2), S = (–2,1,3)$

10. $T = (–2,3,–4), U = (2,0,–3), V = (–2,0,0), W = (–3,–1,–2)$

Exercise $\PageIndex{11}-\PageIndex{14}$

In problems 11 – 14, calculate the distances between the given points

11. $A = (5,3,4), B = (3,4,4)$

12. $A = (6,2,1), B = (3,2,1)$

13. $A = (3,4,2), B = (–1,6,–2)$

14. $A = (–1,5,0), B = (1,3,2)$

Exercise $\PageIndex{15}-\PageIndex{18}$

In problems 15 – 18, graph the given planes.

15. $y = 1$ and $z = 2$	16. $x = 4$ and $y = 2$
17. $x = 1$ and $y = 0$	18. $x = 2$ and $z = 0$

Exercise $\PageIndex{19}-\PageIndex{22}$

In problems 19 – 22, the center and radius of a sphere are given. Find an equation for the sphere.

19. Center = (4, 3, 5), radius = 3	20. Center = (0, 3, 6), radius = 2
21. Center = (5, 1, 0), radius = 5	22. Center = (1, 2, 3), radius = 4

Exercise $\PageIndex{23}-\PageIndex{24}$

In problems 23 – 24, the equation of a sphere is given. Find the center and radius of the sphere.

23. $(x–3)^2 + (y+4)^2 + (z–1)^2 = 16$

24. $(x+2)^2 + y^2 + (z–4)^2 = 25$

Exercise $\PageIndex{25}-\PageIndex{30}$

For problems 25 through 30. Match the contour diagram to the computer-generated, perspective drawing (a through f) it matches. Briefly explain your answer.

25.

26.

27.

28.

29.

30.

a.

b.

c.

d.

e.

f.

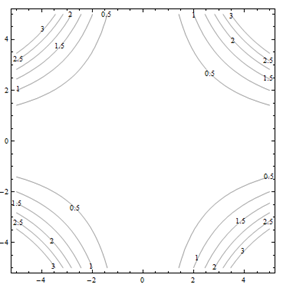
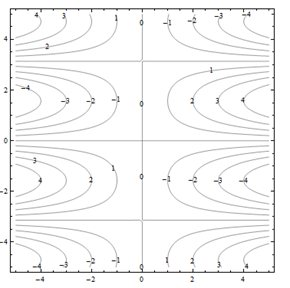
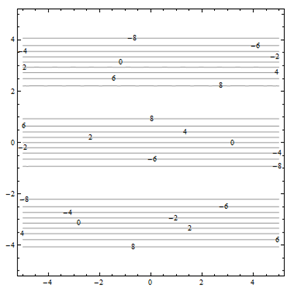
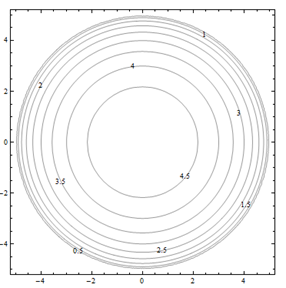
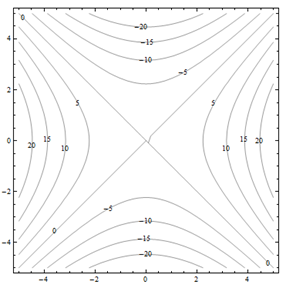
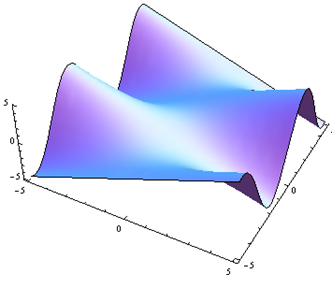
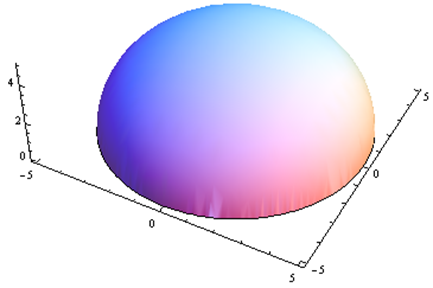
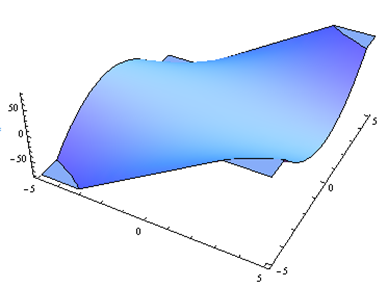
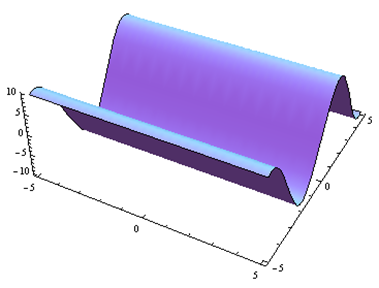
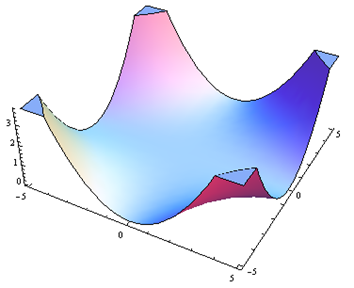
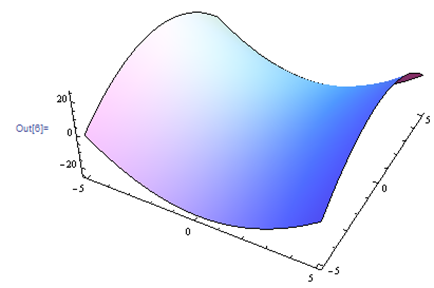
Exercise $\PageIndex{31}-\PageIndex{36}$

For problems 31 through 36. Match the contour diagram to the equation (a through f) it matches. Briefly explain your answer.

31.

32.

33.

34.

35.

36.

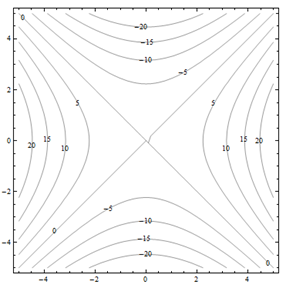
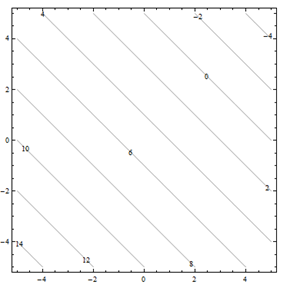
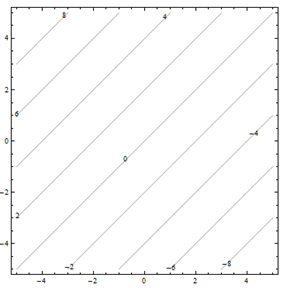
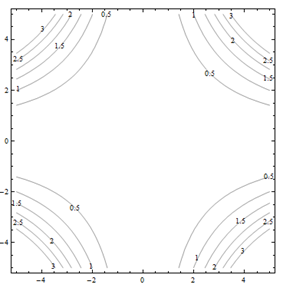
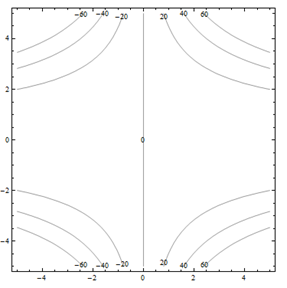
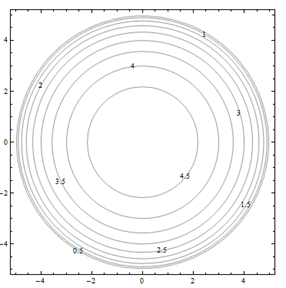
a. $f(x,y) = y-x$	b. $f(x,y) = xy^2$
c. $f(x,y) = \sqrt{25-x^2-y^2}$	d. $f(x,y) = 5-x-y$
e. $f(x,y) = 0.01x^2y^2$	f. $f(x,y) = x^2-y^2$

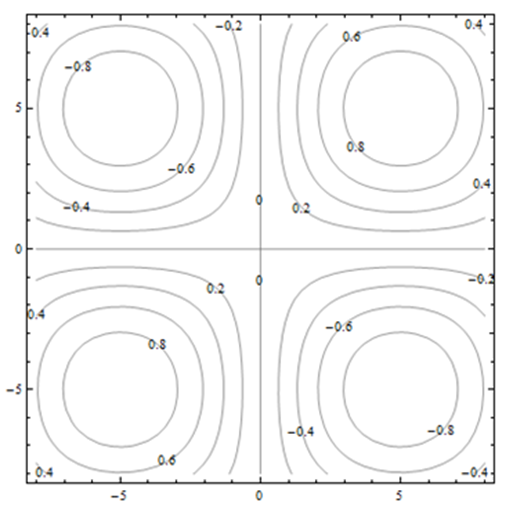
Exercise $\PageIndex{37}$

The contour diagram shown is for a function $M(x, y)$.

Use the diagram to answer the following:

a) Estimate $M(1, 3)$

b) Estimate $M(3, 1)$

c) Is $M(x, 3)$ an increasing or decreasing function of $x$?

d) Is $M(3, y)$ an increasing or decreasing function of $y$?

e) Find a value of $c$ so that $M(c, y)$ is a constant function of $y$.

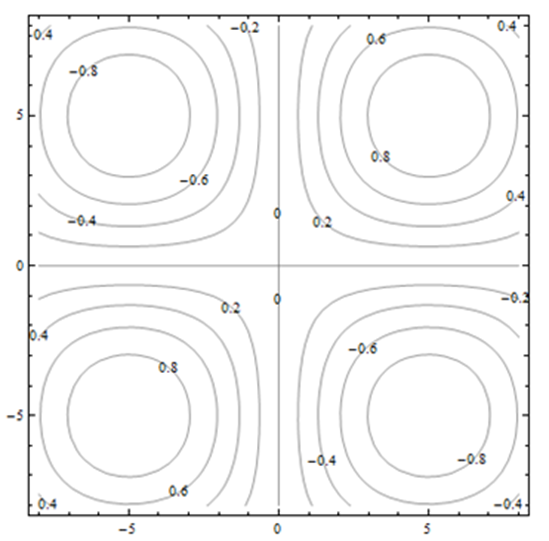
Exercise $\PageIndex{38}$

The contour diagram shown is for a function $G(x, y)$.

Use the diagram to answer the following:

a) Estimate $G(2, 3)$

b) Suppose you travel north (in the direction of increasing $y$) along the surface, starting above (2, 3). Describe your journey.

c) Suppose you travel east (in the direction of increasing $x$) along the surface, starting above (2, 3). Describe your journey.

Exercise $\PageIndex{39}$

The demand functions for two products are given below. $p_1$, $p_2$, $q_1$, and $q_2$ are the prices (in dollars) and quantities for products 1 and 2. Are these two products complementary goods or substitute goods

$$q_1 = 200 -3p_1 + p_2 \nonumber$$

$$q_2 = 150 + p_1 -2p_2 \nonumber$$

Exercise $\PageIndex{40}$

The demand functions for two products are given below. $p_1$, $p_2$, $q_1$, and $q_2$ are the prices (in dollars) and quantities for products 1 and 2. Are these two products complementary goods or substitute goods

$$q_1 = 350 + p_1 + 2p_2 \nonumber$$

$$q_2 = 225 + p_1 + p_2 \nonumber$$

Exercise $\PageIndex{41}$

Consider the Cobb-Douglas Production function: $P(L,K) = 11 L^{0.3} K^{0.7}$. Find the total units of production when 19 units of labor and 12 units of capital are invested.

Exercise $\PageIndex{42}$

Consider the Cobb-Douglas Production function: $P(L,K) = 6 L^{0.6} K^{0.4}$. Find the total units of production when 24 units of labor and 8 units of capital are invested.

4.2 Exercises

Exercise $\PageIndex{1}-\PageIndex{16}$

For problems 1 through 16, find $f_x$ and $f_y$ for the function given

1. $f(x,y) = x^2-5y^2$

2. $f(x,y) = \frac{x^2-5y^2}{x+4}$

3. $f(x,y) = e^{x+6y}$

4. $f(x,y) = (x^2-5y^2) e^x$

5. $f(x,y) = (x^2 - 5y^2) \left(\frac{1}{3y}+4\right)$

6. $f(x,y) = x$

7. $f(x,y) = 6$

8. $f(x,y) = \ln (xy+2x-6y)$

9. $f(x,y) = \frac{x^2-5y^2}{y^4-5x^4}$

10. $f(x,y) = e^{\sqrt{x-4y}} (x-4y)$

11. $f(x,y) = y^5 e^x$

12. $f(x,y) = \frac{1}{16xy}$

13. $f(x,y) = (x+e^y)^7$

14. $f(x,y) = x^4 + 4x^3y - 6x^2y^2 - 4xy^3 + y^4$

15. $f(x,y) = \sqrt{x+\sqrt{y}}$

16. $f(x,y) = x^2y^3-4x^3$

Exercise $\PageIndex{17}$

Here is a table showing the function $A(t,r)$

$\overset{t}{\downarrow} \ r\rightarrow$	.03	.04	.05	.06	.07
1	30.45	40.81	51.27	61.84	72.51
2	61.84	83.29	105.17	127.50	150.27
3	94.17	127.50	161.83	197.22	233.68

a. Estimate $A_t (2, .05)$.

b. Estimate $A_r (2, .05)$

c. Use your answers to parts a and b to estimate the value of $A (2.5, .054)$

d. The values in the table came from $A(t,r)=1000 (e^{rt} - 1)$, which shows the interest earned if 1000 dollars is deposited in an account earning r annual interest, compounded continuously, and left there for $t$ years. How close are your estimates from parts a, b, and c?

Exercise $\PageIndex{18}$

18. Here is a table showing values for the function $H(t,h)$.

$\overset{t}{\downarrow} \ h\rightarrow$	100	150	200
0	100	150	200
1	110.1	160.1	210.1
2	110.4	160.4	210.4
3	100.9	150.9	200.9
4	81.6	131.6	181.6
5	52.5	102.5	152.5

a. Estimate the value of $\frac{\partial H}{dt}$ at (3, 150).

b. Estimate the value of $\frac{\partial H}{dh}$ at (3, 150).

c. Use your answers to parts a and b to estimate the value of $H(2.6, 156)$.

d. The values in the table came from $H (t,h) = h + 15t - 4.9t^2$, which gives the height in meters above the ground after $t$ seconds of an object that is thrown upward from an initial height of $h$ meters with an initial velocity of 15 meters per second. How close are your estimates from parts a, b, and c?

Exercise $\PageIndex{19}$

Given the function $f(x,y) = x^2\sqrt{y}$

a. Calculate $f(2,4)$, $f_x (2,4)$, and $f_y(2,4)$

b. Use your answers from part $a$ to estimate $f(1.9, 4.1)$

Exercise $\PageIndex{20}$

Given the function $f(x,y) = \ln (10 - x^2 - y)$

a. Calculate $f(2,5)$, $f_x (2,5)$, and $f_y(2,5)$

b. Use your answers from part $a$ to estimate $f(1.8,4.8)$

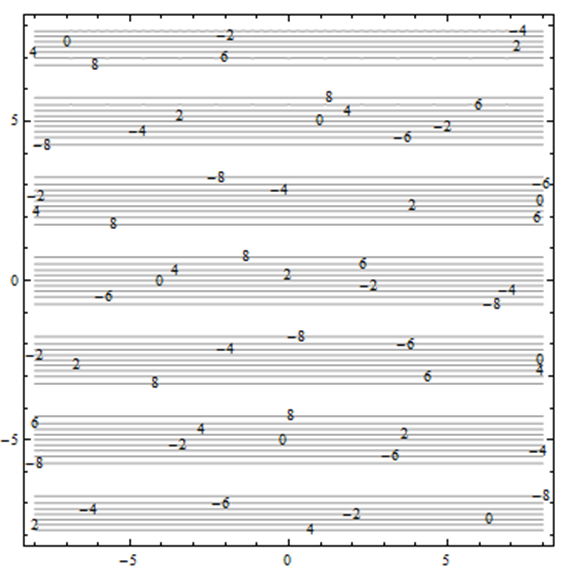
Exercise $\PageIndex{21}-\PageIndex{26}$

In problems 21 - 26, use the contour plot shown to estimate the desired value.

21. $f_x(1,-5)$

22. $f_x(-5,2)$

23. $f_x(5,5)$

24. $f_x(0,0)$

25. $f_y(1,-5)$

26. $f_y(-5,2)$

4.3 Exercises

Exercise $\PageIndex{1}-\PageIndex{6}$

For problems 1 through 6, find $f_{xx}$, $f_{yy}$, $f_{xy}$ and $f_{yx}$ for the function given. Confirm that $f_{xy} = f_{yx}$.

1. $f(x,y) = x^2-5y^2$

2. $f(x,y) = x^4+4x^3y-6x^2y^y-4xy^3+y^4$

3. $f(x,y) = 5x^2y^2$

4. $f(x,y) = e^{x+6y}$

5. $f(x,y) = \ln (xy + 2x - 6y)$

6. $f(x,y) = \frac{x^2}{y^4-5}$

Exercise $\PageIndex{7}$

Find the critical points of $f(x,y) = y^3 - x^3 + 15x^2 - 12y + 12$ and use the Second Derivative Test to classify them. If the test fails, say “the test fails.”

Exercise $\PageIndex{8}$

Find the critical points of $f(x,y) = 2xy-x^2-2y^2+6x+4$ and use the Second Derivative Test to classify them. If the test fails, say “the test fails.”

Exercise $\PageIndex{9}$

Find the critical points of $f(x,y)=y^2-4 \ln (x) + 4x$ and use the Second Derivative Test to classify them. If the test fails, say “the test fails.”

Exercise $\PageIndex{10}$

Find the critical points of $f(x,y)= xy - 6x^2 + 3x -y+2$ and use the Second Derivative Test to classify them. If the test fails, say “the test fails.”

Exercise $\PageIndex{11}$

The origin is a critical point for the function $f(x,y) = x^3+y^3$, and $D = 0$ there. That is, the Second Derivative Test fails. Use what you know about shapes of functions to decide if there is a local minimum, local maximum, or saddle point for this function at (0, 0).

Exercise $\PageIndex{12}$

The origin is a critical point for the function $f(x,y) = 15 - x^2y^2$, and $D = 0$ there. That is, the Second Derivative Test fails. Use what you know about shapes of functions to decide if there is a local minimum, local maximum, or saddle point for this function at (0, 0).

Exercise $\PageIndex{13}-\PageIndex{18}$

For problems 13 through 18, find all local maxima, minima, and saddle points for the function.

13. $f(x,y) = xy -5x^2 - 5y^2 + 33y$

14. $f(x,y) = 10xy-x^2-y^2+3x$

15. $f(x,y) = x^3+y^3-3xy$

16. $f(x,y) = 5x^2-4xy+2y^2+4x-4y+10$

17. $f(x,y) = y^2e^x+x^2$

18. $f(x,y) = xy+2x-\ln (x^2y)$, for $x>0$ and $y>0$.

Exercise $\PageIndex{19}$

The demand functions for two products are given below. $p_1$, $p_2$, $q_1$, and $q_2$ are the prices (in dollars) and quantities for products 1 and 2.

$$q_1 = 200+3p_1+p_2 \nonumber$$

$$q_2=150+p_1+2p_2\nonumber$$

a. Are these two products complementary goods or substitute goods?

b. What is the quantity demanded for each when the price for product 1 is $20 per item and the price for product 2 is $30 per item?

c. Write a function $R(p_1,p_2)$ that expresses the total revenue from these two products.

d. Find the price and quantity for each product that maximizes the total revenue.

Exercise $\PageIndex{20}$

The demand functions for two products are given below. $p_1$, $p_2$, $q_1$, and $q_2$ are the prices (in dollars) and quantities for products 1 and 2.

$$q_1 = 350+p_1+2p_2 \nonumber$$

$$q_2=225+p_1+p_2\nonumber$$

a. Are these two products complementary goods or substitute goods?

b. What is the quantity demanded for each when the price for product 1 is $20 per item and the price for product 2 is $30 per item?

c. Write a function $R(p_1,p_2)$ that expresses the total revenue from these two products.

d. Find the price and quantity for each product that maximizes the total revenue.

Exercise $\PageIndex{21}$

Suppose the demand functions for two products are $q_1 = f(p_1, p_2)$ and $q_2 = g(p_1, p_2)$, where $p_1$, $p_2$, $q_1$, and $q_2$ are the prices (in dollars) and quantities for products 1 and 2. Consider the four partial derivatives $\frac{\partial q_1}{\partial p_1}$, $\frac{\partial q_1}{\partial p_2}$, $\frac{\partial q_2}{\partial p_1}$, and $\frac{\partial q_2}{\partial p_2}$. Tell the sign of each of these partial derivatives if

a. the products are complementary goods.

b. the products are substitute goods.