8.5: Polar Form of Complex Numbers

Plotting Complex Numbers in the Complex Plane

Plotting a complex number \(a+bi\) is similar to plotting a real number, except that the horizontal axis represents the real part of the number, \(a\), and the vertical axis represents the imaginary part of the number, \(bi\).

How to: Given a complex number \(a+bi\), plot it in the complex plane.

1. Label the horizontal axis as the real axis and the vertical axis as the imaginary axis.
2. Plot the point in the complex plane by moving \(a\) units in the horizontal direction and \(b\) units in the vertical direction.

Example \(\PageIndex{1}\): Plotting a Complex Number in the Complex Plane

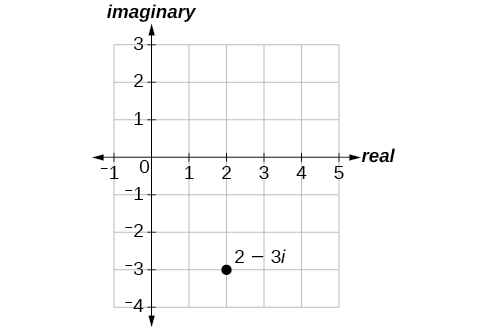
Plot the complex number \(2−3i\) in the complex plane.

Solution

From the origin, move two units in the positive horizontal direction and three units in the negative vertical direction. See Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\)

Finding the Absolute Value of a Complex Number

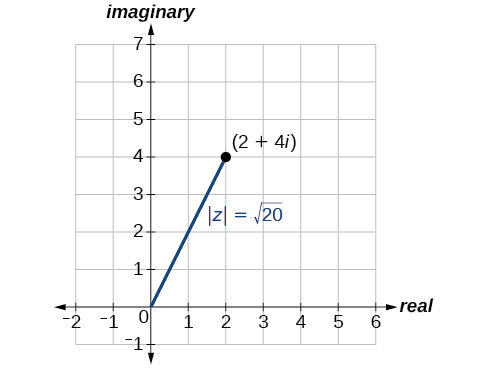
The first step toward working with a complex number in polar form is to find the absolute value. The absolute value of a complex number is the same as its magnitude, or \(| z |\). It measures the distance from the origin to a point in the plane. For example, the graph of \(z=2+4i\), in Figure \(\PageIndex{3}\), shows \(| z |\).

Figure \(\PageIndex{3}\)

ABSOLUTE VALUE OF A COMPLEX NUMBER

Given \(z=x+yi\), a complex number, the absolute value of \(z\) is defined as

\[| z |=\sqrt{x^2+y^2}\]

It is the distance from the origin to the point \((x,y)\).

Notice that the absolute value of a real number gives the distance of the number from \(0\), while the absolute value of a complex number gives the distance of the number from the origin, \((0, 0)\).

Example \(\PageIndex{2}\): Finding the Absolute Value of a Complex Number with a Radical

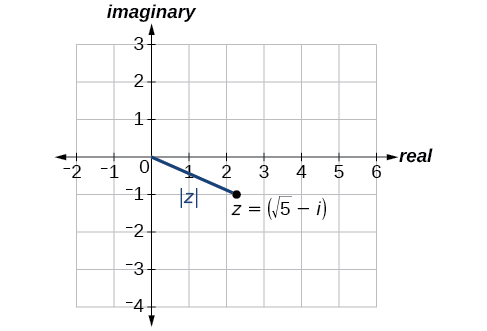
Find the absolute value of \(z=\sqrt{5}−i\).

Solution

Using the formula, we have

\[\begin{align*} |z| &= \sqrt{x^2+y^2} \\ |z| &= \sqrt{{(\sqrt{5})}^2+{(-1)}^2} \\ |z| &= \sqrt{5+1} \\ |z| &= \sqrt{6} \end{align*}\]

See Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\)

Writing Complex Numbers in Polar Form

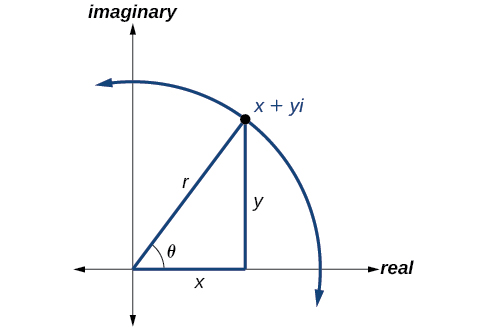
The polar form of a complex number expresses a number in terms of an angle \(\theta\) and its distance from the origin \(r\). Given a complex number in rectangular form expressed as \(z=x+yi\), we use the same conversion formulas as we do to write the number in trigonometric form:

\[\begin{align*} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align*}\]

We review these relationships in Figure \(\PageIndex{6}\).

Figure \(\PageIndex{6}\)

We use the term modulus to represent the absolute value of a complex number, or the distance from the origin to the point \((x,y)\). The modulus, then, is the same as \(r\), the radius in polar form. We use \(\theta\) to indicate the angle of direction (just as with polar coordinates). Substituting, we have

\[\begin{align*} z &= x+yi \\ z &= r \cos \theta+(r \sin \theta)i \\ z &= r(\cos \theta+i \sin \theta) \end{align*}\]

POLAR FORM OF A COMPLEX NUMBER

Writing a complex number in polar form involves the following conversion formulas:

\[\begin{align} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align}\]

Making a direct substitution, we have

\[\begin{align} z &= x+yi \\ z &= (r \cos \theta)+i(r \sin \theta) \\ z &= r(\cos \theta+i \sin \theta) \end{align}\]

where \(r\) is the modulus and \(\theta\) is the argument. We often use the abbreviation \(r\; cis \theta\) to represent \(r(\cos \theta+i \sin \theta)\).

Example \(\PageIndex{4}\): Expressing a Complex Number Using Polar Coordinates

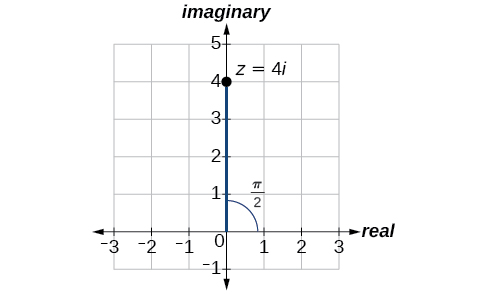
Express the complex number \(4i\) using polar coordinates.

Solution

On the complex plane, the number \(z=4i\) is the same as \(z=0+4i\). Writing it in polar form, we have to calculate \(r\) first.

\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{0^2+4^2} \\ r &= \sqrt{16} \\ r &= 4 \end{align*}\]

Next, we look at \(x\). If \(x=r \cos \theta\), and \(x=0\), then \(\theta=\dfrac{\pi}{2}\). In polar coordinates, the complex number \(z=0+4i\) can be written as \(z=4\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right) \text{ or } 4\; cis\left( \dfrac{\pi}{2}\right)\). See Figure \(\PageIndex{7}\).

Figure \(\PageIndex{7}\)

Finding Products of Complex Numbers in Polar Form

Now that we can convert complex numbers to polar form we will learn how to perform operations on complex numbers in polar form. For the rest of this section, we will work with formulas developed by French mathematician Abraham de Moivre (1667-1754). These formulas have made working with products, quotients, powers, and roots of complex numbers much simpler than they appear. The rules are based on multiplying the moduli and adding the arguments.

PRODUCTS OF COMPLEX NUMBERS IN POLAR FORM

If \(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) and \(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), then the product of these numbers is given as:

\[\begin{align} z_1z_2 &= r_1r_2[ \cos(\theta_1+\theta_2)+i \sin(\theta_1+\theta_2) ] \\ z_1z_2 &= r_1r_2\space cis(\theta_1+\theta_2) \end{align}\]

Notice that the product calls for multiplying the moduli and adding the angles.

Example \(\PageIndex{7}\): Finding the Product of Two Complex Numbers in Polar Form

Find the product of \(z_1z_2\), given \(z_1=4(\cos(80°)+i \sin(80°))\) and \(z_2=2(\cos(145°)+i \sin(145°))\).

Solution

Follow the formula

\[\begin{align*} z_1z_2 &= 4⋅2[\cos(80°+145°)+i \sin(80°+145°)] \\ z_1z_2 &= 8[\cos(225°)+i \sin(225°)] \\ z_1z_2 &= 8\left[\cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ z_1z_2 &= 8\left[−\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ z_1z_2 &= −4\sqrt{2}−4i\sqrt{2} \end{align*}\]

Finding Quotients of Complex Numbers in Polar Form

The quotient of two complex numbers in polar form is the quotient of the two moduli and the difference of the two arguments.

QUOTIENTS OF COMPLEX NUMBERS IN POLAR FORM

If \(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) and \(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), then the quotient of these numbers is

\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}[\cos(\theta_1−\theta_2)+i \sin(\theta_1−\theta_2) ],\space z_2≠0\]

\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}\space cis(\theta_1−\theta_2),\space z_2≠0\]

Notice that the moduli are divided, and the angles are subtracted.

How to: Given two complex numbers in polar form, find the quotient

1. Divide \(\dfrac{r_1}{r_2}\).
2. Find \(\theta_1−\theta_2\).
3. Substitute the results into the formula: \(z=r(\cos \theta+i \sin \theta)\). Replace \(r\) with \(\dfrac{r_1}{r_2}\), and replace \(\theta\) with \(\theta_1−\theta_2\).
4. Calculate the new trigonometric expressions and multiply through by \(r\).

Example \(\PageIndex{8}\): Finding the Quotient of Two Complex Numbers

Find the quotient of \(z_1=2(\cos(213°)+i \sin(213°))\) and \(z_2=4(\cos(33°)+i \sin(33°))\).

Solution

Using the formula, we have

\[\begin{align*} \dfrac{z_1}{z_2} &= \dfrac{2}{4}[\cos(213°−33°)+i \sin(213°−33°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[\cos(180°)+i \sin(180°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[−1+0i] \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2}+0i \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2} \end{align*}\]

Finding Powers of Complex Numbers in Polar Form

Finding powers of complex numbers is greatly simplified using De Moivre’s Theorem. It states that, for a positive integer \(n\), \(z^n\) is found by raising the modulus to the \(n^{th}\) power and multiplying the argument by \(n\). It is the standard method used in modern mathematics.

DE MOIVRE’S THEOREM

If \(z=r(\cos \theta+i \sin \theta)\) is a complex number, then

\[\begin{align} z^n &= r^n[\cos(n\theta)+i \sin(n\theta) ] \\ z^n &= r^n\space cis(n\theta) \end{align}\]

where \(n\) is a positive integer.

Example \(\PageIndex{9}\): Evaluating an Expression Using De Moivre’s Theorem

Evaluate the expression \({(1+i)}^5\) using De Moivre’s Theorem.

Solution

Since De Moivre’s Theorem applies to complex numbers written in polar form, we must first write \((1+i)\) in polar form. Let us find \(r\).

\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(1)}^2+{(1)}^2} \\ r &= \sqrt{2} \end{align*}\]

Then we find \(\theta\). Using the formula \(\tan \theta=\dfrac{y}{x}\) gives

\[\begin{align*} \tan \theta &= \dfrac{1}{1} \\ \tan \theta &= 1 \\ \theta &= \dfrac{\pi}{4} \end{align*}\]

Use De Moivre’s Theorem to evaluate the expression.

\[\begin{align*} {(a+bi)}^n &= r^n[\cos(n\theta)+i \sin(n\theta)] \\ {(1+i)}^5 &= {(\sqrt{2})}^5\left[ \cos\left(5⋅\dfrac{\pi}{4}\right)+i \sin\left(5⋅\dfrac{\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ \cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ −\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ {(1+i)}^5 &= −4−4i \end{align*}\]

Finding Roots of Complex Numbers in Polar Form

To find the \(n^{th}\) root of a complex number in polar form, we use the \(n^{th}\) Root Theorem or De Moivre’s Theorem and raise the complex number to a power with a rational exponent. There are several ways to represent a formula for finding \(n^{th}\) roots of complex numbers in polar form.

THE \(N^{TH}\) ROOT THEOREM

To find the \(n^{th}\) root of a complex number in polar form, use the formula given as

\[z^{\tfrac{1}{n}}=r^{\tfrac{1}{n}}\left[ \cos\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right)+i \sin\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right) \right]\]

where \(k=0, 1, 2, 3, . . . , n−1\). We add \(\dfrac{2k\pi}{n}\) to \(\dfrac{\theta}{n}\) in order to obtain the periodic roots.

th Root of a Complex Number

Evaluate the cube roots of \(z=8\left(\cos\left(\frac{2\pi}{3}\right)+i\sin\left(\frac{2\pi}{3}\right)\right)\).

Solution

We have

\[\begin{align*} z^{\frac{1}{3}} &= 8^{\frac{1}{3}}\left[ \cos\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right) \right] \\ z^{\frac{1}{3}} &= 2\left[ \cos\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right) \right] \end{align*}\]

There will be three roots: \(k=0, 1, 2\). When \(k=0\), we have

\(z^{\frac{1}{3}}=2\left(\cos\left(\dfrac{2\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}\right)\right)\)

When \(k=1\), we have

\[\begin{align*} z^{\frac{1}{3}} &=2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right) \right] \;\;\;\;\;\;\;\;\; \text{Add }\dfrac{2(1)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{8\pi}{9}\right)+i \sin\left(\dfrac{8\pi}{9}\right)\right) \end{align*}\]

When \(k=2\), we have

\[\begin{align*} z^{\frac{1}{3}} &= 2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right) \right] \;\;\;\;\;\;\; \text{Add }\dfrac{2(2)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{14\pi}{9}\right)+i \sin\left(\dfrac{14\pi}{9}\right)\right) \end{align*}\]

Remember to find the common denominator to simplify fractions in situations like this one. For \(k=1\), the angle simplification is

\[\begin{align*} \dfrac{\dfrac{2\pi}{3}}{3}+\dfrac{2(1)\pi}{3} &= \dfrac{2\pi}{3}(\dfrac{1}{3})+\dfrac{2(1)\pi}{3}\left(\dfrac{3}{3}\right) \\ &=\dfrac{2\pi}{9}+\dfrac{6\pi}{9} \\ &=\dfrac{8\pi}{9} \end{align*}\]