6.2.3: Solid Geometric Figures and Objects

Last updated
Save as PDF

Page ID: 87302

Leah Griffith, Veronica Holbrook, Johnny Johnson & Nancy Garcia
Rio Hondo College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

6.2.3 Learning Objectives

Find the volume of some common geometric objects

The Meaning and Notation for Volume

The product $\text{(length unit)}\text{(length unit)}\text{(length unit)} = \text{(length unit)}^3$, or cubic length unit (cu length unit), can be interpreted physically as the volume of a three-dimensional object.

Definition: Volume

The volume of an object is the amount of cubic length units contained in the object.

For example, 4 cu mm means that 4 cubes, 1 mm on each side, would precisely fill some three-dimensional object. (The cubes may have to be cut and rearranged so they match the shape of the object.)

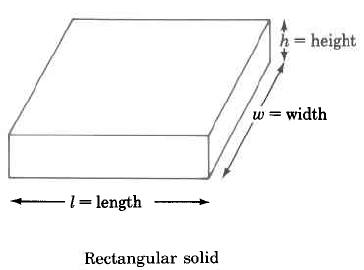
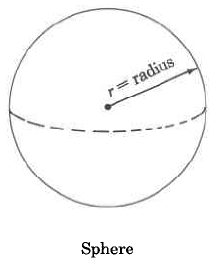
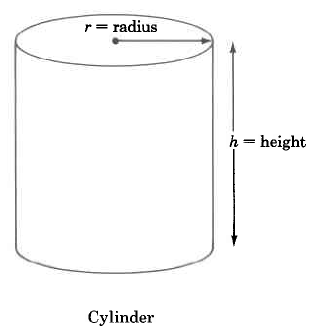
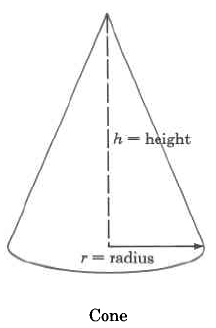
$A rectangular solid, with length l, width w, and height h.$ $A sphere with radius r.$ $A cylinder with height h and radius r.$ $A cone with height h and radius r.$

Volume Formulas

	Figure	Volume Formula	Statement
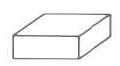$A rectangular solid.$	Rectangular solid	$\begin{array} {rcl} {V_R} & = & {l \cdot w \cdot h} \\ {} & = & {\text{(area of base)} \cdot \text{(height)}} \end{array}$	The volume of a rectangular solid is the length times the width times the height.
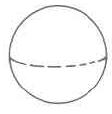$A sphere.$	Sphere	$V_s = \dfrac{4}{3} \cdot \pi \cdot r^3$	The volume of a sphere is $\dfrac{4}{3}$ times $\pi$ times the cube of the radius.
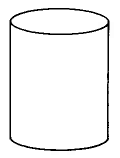$A cylinder.$	Cylinder	$\begin{array} {rcl} {V_{Cyl}} & = & {\pi \cdot r^2 \cdot h} \\ {} & = & {\text{(area of base)} \cdot \text{(height)}} \end{array}$	The volume of a cylinder is $\pi$ times the square of the radius times the height.
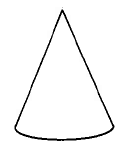$A cone.$	Cone	$\begin{array} {rcl} {V_c} & = & {\dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h} \\ {} & = & {\text{(area of base)} \cdot \text{(height)}} \end{array}$	The volume of a cone is $\dfrac{1}{3}$ times $\pi$ times the square of the radius times the height.

Finding Volumes of Some Common Geometric Objects

Example 1

Find the volume of the rectangular solid.

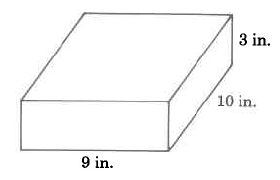
$A rectangular solid with width 9in, length 10in, and height 3in.$

Solution

$\begin{array} {rcl} {V_R} & = & {l \cdot w \cdot h} \\ {} & = & {\text{9 in} \cdot \text{10 in.} \cdot \text{3 in}} \\ {} & = & {\text{270 cu in}} \\ {} & = & {\text{270 in}^3} \end{array}$

The volume of this rectangular solid is 270 cu in.

Example 2

Find the approximate volume of the sphere.

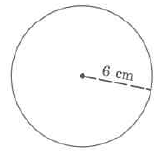
$A circle with radius 6cm.$

Solution

$\begin{array} {rcl} {V_S} & = & {\dfrac{4}{3} \cdot \pi \cdot r^3} \\ {} & \approx & {(\dfrac{4}{3}) \cdot (3.14) \cdot \text{(6 cm)}^3} \\ {} & \approx & {(\dfrac{4}{3}) \cdot (3.14) \cdot \text{(216 cu cm)}} \\ {} & \approx & {\text{904.32 cu cm}} \end{array}$

The approximate volume of this sphere is 904.32 cu cm, which is often written as 904.32 cm$^3$.

Example 3

Find the approximate volume of the cylinder.

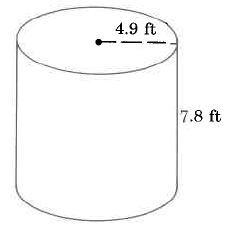
$A cylinder with radius 4.9ft and height 7.8ft.$

Solution

$\begin{array} {rcl} {V_{Cyl}} & = & {\pi \cdot r^2 \cdot h} \\ {} & \approx & {(3.14) \cdot (\text{4.9 ft})^2 \cdot \text{(7.8 ft)}} \\ {} & \approx & {(3.14) \cdot (\text{24.01 sq ft}) \cdot \text{(7.8 ft)}} \\ {} & \approx & {(3.14) \cdot \text{(187.278 cu ft)}} \\ {} & \approx & {\text{588.05292 cu ft}} \end{array}$

The volume of this cylinder is approximately 588.05292 cu ft. The volume is approximate because we approximated $\pi$.

Example 4

Find the approximate volume of the cone. Round to two decimal places.

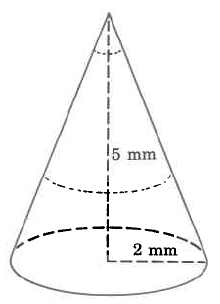
$A cone with height 5mm and radius 2mm$

Solution

$\begin{array} {rcl} {V_{c}} & = & {\dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h} \\{} & \approx & {(\dfrac{1}{3}) \cdot (3.14) \cdot (\text{2 mm})^2 \cdot \text{(5 mm)}} \\ {} & \approx & {(\dfrac{1}{3}) \cdot (3.14) \cdot (\text{4 sq mm}) \cdot \text{(5 mm)}} \\ {} & \approx & {(\dfrac{1}{3}) \cdot (3.14) \cdot \text{(20 cu mm)}} \\ {} & \approx & {20.9\overline{3} \text{ cu mm}} \\ {} & \approx & {\text{20.93 cu mm}} \end{array}$

The volume of this cone is approximately 20.93 cu mm. The volume is approximate because we approximated $\pi$.

Try It Now 1

Find the volume of the rectangular solid.

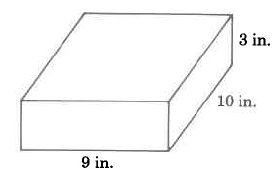
$A rectangular solid with width 9in, length 10in, and height 3in.$

Answer: 21 cu in

Try It Now 2

Find the volume of the sphere. Use the $\pi$ key on your calculator to find the approximate volume.

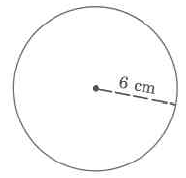
$A sphere with radius 6cm.$

Answer: 904.32 cu ft

Try It Now 3

Find the volume of the cylinder. Use the $\pi$ key on your calculator to find the approximate volume.

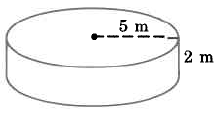
$A cylinder with radius 5m and height 2m.$

Answer: 157 cu m

Try It Now 4

Find the volume of the cone. Use the $\pi$ key on your calculator to find the approximate volume.

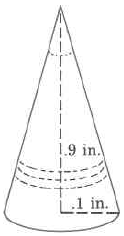
$A cone with height .9in and radius .1 in.$

Answer: 0.00942 cu in

Finding the Volume of Composite Figures

Similar to finding the area of composite figures, we will first determine the separate shapes that the figure is made of. Then use the formulas for the volumes of the individual shapes and add them together.

Example 5

Find the approximate volume of the composite figure. Use the $\pi$ key on your calculator to find the approximate volume if necessary. Round to two decimal places.

$A cylinder with a cone on top. The object has a diameter of 3.0ft. The cone has a height of 3.0ft. The cylinder's height is 8.1ft.$

Solution

This shape is made up of a cone and a cylinder. We can tell from the base of the cylinder, that the diameter of the cone is 3.0 ft.

$\begin{array} {rcl} {V} & = &{V_{cone}+V_{cylinder}}\\{}& = &{\dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h+\pi \cdot r^2 \cdot h}\\{} & \approx & {(\dfrac{1}{3}) \cdot \pi \cdot (\text{1.5 ft})^2 \cdot \text{(3.0 ft)}+\pi \cdot \text{1.5 ft}^2 \cdot \text{8.1 ft.}}\\{} & \approx & {(\dfrac{1}{3}) \cdot \pi \cdot (\text{2.25 ft}^2) \cdot \text{(3.0 ft)}+\pi \cdot \text{2.25 ft}^2 \cdot \text{8.1 ft.}}\\{} & \approx & {(\dfrac{1}{3}) \cdot \pi \cdot \text{(6.75 cu ft)}+\pi \cdot \text{18.225 cu ft}}\\{} & \approx & {7.06858 \text{ cu ft}+57.25553\text{ cu ft}} \\{} & \approx & {\text{64.32 cu ft}} \end{array}$

The volume of this figure is approximately 64.32 cu ft. The volume is approximate because we approximated $\pi$.

Try It Now 6

Find the volume of the composite figure.

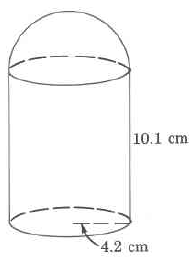
$A cylinder with a half-sphere on top. The object's radius is 4.2cm, and the cylinder's height is 10.1cm.$

Answer

This shape is composed of a hemisphere and a cylinder.

$V\approx 870$ cu cm

Search

Text Color

Text Size

Margin Size

Font Type

Volume Formulas