1.8: Relating Trigonometric Functions

Last updated
Save as PDF

Page ID: 61238

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

State the reciprocal relationships between trig functions, and use these identities to find values of trig functions.
State quotient relationships between trig functions, and use quotient identities to find values of trig functions.
State the domain and range of each trig function.
State the sign of a trig function, given the quadrant in which an angle lies.
State the Pythagorean identities and use these identities to find values of trig functions.

Reciprocal and Pythagorean Identities

The two most basic types of trigonometric identities are the reciprocal identities and the Pythagorean identities. The reciprocal identities are simply definitions of the reciprocals of the three standard trigonometric ratios:
\[ \sec \theta=\frac{1}{\cos \theta} \quad \csc \theta=\frac{1}{\sin \theta} \quad \cot \theta=\frac{1}{\tan \theta}
\]

Also, recall the definitions of the three standard trigonometric ratios (sine, cosine and tangent):
\[ \begin{array}{l}
\sin \theta=\frac{o p p}{h y p} \\
\cos \theta=\frac{a d j}{h y p} \\
\tan \theta=\frac{o p p}{a d y}
\end{array}
\]

If we look more closely at the relationships between the sine, cosine and tangent, we'll notice that $\frac{\sin \theta}{\cos \theta}=\tan \theta$
\[ \frac{\sin \theta}{\cos \theta}=\frac{\left(\frac{o p p}{h y p}\right)}{\left(\frac{a d j}{h y p}\right)}=\frac{o p p}{h y p} * \frac{h y p}{a d j}=\frac{o p p}{a d j}=\tan \theta
\]

Pythagorean Identities
The Pythagorean Identities are, of course, based on the Pythagorean Theorem. If we recall a diagram that was introduced in Chapter $2,$ we can build these identities from the relationships in the diagram:

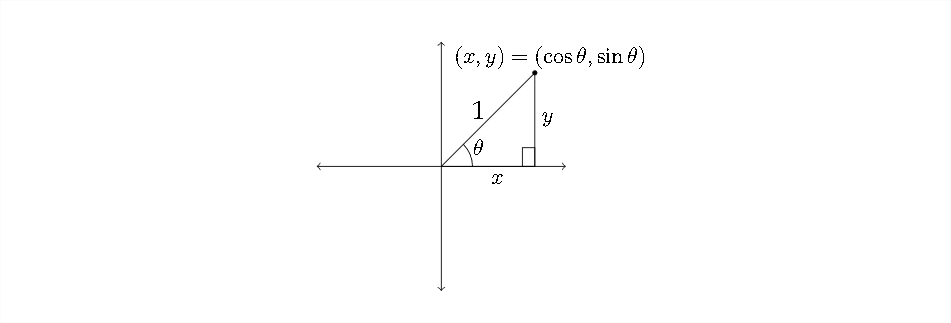
$clipboard_ed780c7fde91ea675bea981d3e4178732.png$

Using the Pythagorean Theorem in this diagram, we see that $x^{2}+y^{2}=1^{2},$ so $x^{2}+y^{2}=1 .$ But, also remember that, in the unit circle, $x=\cos \theta$ and $y=\sin \theta$

Substituting this equality gives us the first Pythagorean Identity:
\[ x^{2}+y^{2}=1
\] or
\[ \cos ^{2} \theta+\sin ^{2} \theta=1
\] This identity is usually stated in the form:
\[ \sin ^{2} \theta+\cos ^{2} \theta=1
\]

If we take this identity and divide through on both sides by $\cos ^{2} \theta,$ this will result in the first of two additional Pythagorean Identities:
\[ \frac{\sin ^{2} \theta}{\cos ^{2} \theta}+\frac{\cos ^{2} \theta}{\cos ^{2} \theta}=\frac{1}{\cos ^{2} \theta}
\] or
\[ \tan ^{2} \theta+1=\sec ^{2} \theta
\]

Dividing through by $\sin ^{2} \theta$ gives us the second:
\[ \frac{\sin ^{2} \theta}{\sin ^{2} \theta}+\frac{\cos ^{2} \theta}{\sin ^{2} \theta}=\frac{1}{\sin ^{2} \theta}
\] or
\[ 1+\cot ^{2} \theta=\csc ^{2} \theta
\] So, the three Pythagorean Identities we will be using are:
\[ \begin{array}{l}
\sin ^{2} \theta+\cos ^{2} \theta=1 \\
\tan ^{2} \theta+1=\sec ^{2} \theta \\
1+\cot ^{2} \theta=\csc ^{2} \theta
\end{array}
\]

These Pythagorean Identities are often stated in other terms, such as:
\[ \begin{array}{l}
\sin ^{2} \theta=1-\cos ^{2} \theta \\
\cos ^{2} \theta=1-\sin ^{2} \theta \\
\tan ^{2} \theta=\sec ^{2} \theta-1 \\
\cot ^{2} \theta=\csc ^{2} \theta-1
\end{array}
\]

Now that we have some basic identities to work with, let's use them to verify the equality of some more complicated statements. The process of verifying trigonometric identities involves changing one side of the given expression into the other side. since these are not really equations, we will not treat them the way we treat equations. That is to say, we won't add or subtract anything to both sides of the statement (or multiply or divide by anything on both sides either).

Another reason for not treating a trigonometric identity as an equation is that, in practice, this process typically involves just one side of the statement. In problem solving, mathematicians typically use trigonometric identities to change the appearance of a problem without changing its value. In this process, a trigonometric expression is changed into another trigonometric expression rather than showing that two trigonometric expressions are the same, which is what we will be doing.

The trigonometric identities we have discussed in this section are summarized below:

$clipboard_e2e496ea4f227115b2de6bdbf8c87dd10.png$

The form sin $\theta$ or $\cos \theta$ is typically used, however any letter may be used to represent the angle in question so long as it is the SAME letter in all expressions. For example, we can say that:
\[ \sin ^{2} \theta+\cos ^{2} \theta=1
\] or we can say that

\[ \sin ^{2} x+\cos ^{2} x=1
\] however:
\[ \sin ^{2} \theta+\cos ^{2} x \neq 1
\] because $\theta$ and $x$ could be different angles!

Quotient Identities

The definitions of the trig functions led us to the reciprocal identities, which can be seen in the Concept about that topic. They also lead us to another set of identities, the quotient identities.

Consider first the sine, cosine, and tangent functions. For angles of rotation (not necessarily in the unit circle) these functions are defined as follows:

$\begin{aligned}\sin \theta&=\dfrac{y}{r}\\ \cos \theta&=\dfrac{x}{r}\\ \tan \theta &=\dfrac{y}{x}\end{aligned}$

Given these definitions, we can show that $\tan \theta =\dfrac{\sin \theta}{\cos \theta}$, as long as $\cos \theta \neq 0$:

$\dfrac{\sin \theta}{\cos \theta} =\dfrac{\dfrac{y}{r}}{\dfrac{x}{r}}=\dfrac{y}{r}\times \dfrac{r}{x}=\dfrac{y}{x}=\tan \theta$.

The equation $\tan \theta =\dfrac{\sin \theta}{\cos \theta}$ is therefore an identity that we can use to find the value of the tangent function, given the value of the sine and cosine.

Let's take a look at some problems involving quotient identities.

1. Find the value of $\tan \theta$?

If $\cos \theta =\dfrac{5}{13}$ and $\sin \theta =\dfrac{12}{13}$, what is the value of $\tan \theta $?

$\tan \theta =\dfrac{12}{5}$

$\tan \theta =\dfrac{\sin \theta}{\cos \theta} =\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{13}\times \dfrac{13}{5}=\dfrac{12}{5}$

2. Show that $\cot \theta =\dfrac{\cos \theta}{\sin \theta}$

$\cos \theta \sin \theta =\dfrac{\dfrac{x}{r}}{\dfrac{y}{r}}=\dfrac{x}{r}\times\dfrac{r}{y}=\dfrac{x}{y}=\cot \theta$

3. What is the value of $\cot \theta$?

If $\cos \theta =\dfrac{7}{25}$ and $\sin \theta =\dfrac{24}{25}$, what is the value of $\cot \theta$?

$\cot \theta =\dfrac{7}{24}$

$\cot \theta =\dfrac{\cos \theta}{\sin \theta}=\dfrac{\dfrac{7}{25}}{\dfrac{24}{25}}=\dfrac{7}{25}\times \dfrac{25}{24}=\dfrac{7}{24}$

Example $\PageIndex{3}$

If $\sin \theta =\dfrac{63}{65}$ and $\cos \theta =\dfrac{16}{65}$, what is the value of $\tan \theta$?

Solution

$\tan \theta =\dfrac{63}{16}$. We can see this from the relationship for the tangent function:

$\tan \theta =\dfrac{\sin \theta}{\cos \theta}=\dfrac{\dfrac{63}{65}}{\dfrac{16}{65}}=\dfrac{63}{65}\times \dfrac{65}{16}=\dfrac{63}{16}$

Example $\PageIndex{4}$

If $\tan \theta =\dfrac{40}{9}$ and $\cos \theta =\dfrac{9}{41}$, what is the value of $\sin \theta$?

Solution

$\sin \theta =\dfrac{40}{41}$. We can see this from the relationship for the tangent function:

$\begin{aligned} \tan \theta &= \dfrac{\sin \theta}{\cos \theta} \\ \sin \theta &=(\tan \theta )(\cos \theta ) \\ \sin \theta&=\dfrac{40}{9}\times \dfrac{9}{41} \\ \sin \theta &=\dfrac{40}{41}\end{aligned}$

Review

Fill in each blank with a trigonometric function.

If $\cos \theta =\dfrac{1}{2}$ and $\cot \theta =\dfrac{\sqrt{3}}{3}$, what is the value of $\sin \theta $?
If $\tan \theta =0$ and $\cos \theta =−1$, what is the value of $\sin \theta$?
If $\cot \theta =−1$ and $\sin \theta =−\dfrac{\sqrt{2}}{2}$, what is the value of $\cos \theta $?

Vocabulary

Term	Definition
Quotient Identity	The quotient identity is an identity relating the tangent of an angle to the sine of the angle divided by the cosine of the angle.

Additional Resources

Video: The Reciprocal, Quotient, and Pythagorean Identities

Cofunction Identities

A cofunction identity is a relationship between one trig function of an angle and another trig function of the complement of that angle.

In a right triangle, you can apply what are called "cofunction identities". These are called cofunction identities because the functions have common values. These identities are summarized below.

$\begin{array}{rr}
\sin \theta=\cos \left(90^{\circ}-\theta\right) & \cos \theta=\sin \left(90^{\circ}-\theta\right) \\
\tan \theta=\cot \left(90^{\circ}-\theta\right) & \cot \theta=\tan \left(90^{\circ}-\theta\right)
\end{array}$

Example $\PageIndex{1}$

Find the value of $\sin 45^{\circ}$ using a cofunction identity.

Solution

The sine of $45^{\circ}$ is equal to $\cos\left(90^{\circ} −45^{\circ} \right)=\cos 45^{\circ} =\dfrac{\sqrt{2}}{2}$.

Example $\PageIndex{2}$

Find the value of $\cos 45^{\circ}$ using a cofunction identity.

Solution

The cosine of $45^{\circ}$ is equal to $\sin\left(90^{\circ} −45^{\circ} \right)=\sin 45^{\circ} =\dfrac{\sqrt{2}}{2}$.

Example $\PageIndex{3}$

Find the value of $\cos 60^{\circ}$ using a cofunction identity.

Solution

The cosine of $60^{\circ}$ is equal to $\sin\left(90^{\circ} −60^{\circ} \right)=\sin 30^{\circ} =.5$.

Review

Find a value for $\theta$ for which $\sin\theta =\cos15^{\circ}$ is true.
Find a value for $\theta$ for which $\cos\theta =\sin55^{\circ}$ is true.
Find a value for $\theta$ for which $\tan\theta =\cot80^{\circ}$ is true.
Use the sine and cosine cofunction identities to prove that $\tan(90^{\circ} −\theta )=\cot\theta$.

Vocabulary

Term	Definition
Cofunction Identity	A cofunction identity is a relationship between one trig function of an angle and another trig function of the complement of that angle.

Additional Resources

Video: Cofunctions