6.2: Graphing Basic Polar Equations
( \newcommand{\kernel}{\mathrm{null}\,}\)
Learning Objectives
- Graph polar equations.
- Graph and recognize limaçons and cardioids.
- Determine the shape of a limaçon from the polar equation.
Keplar's First Law of Planetary Motion argues that the planets move through space in elliptical, periodic orbits about the sun, as shown in Figure

Testing Polar Equations for Symmetry
Just as a rectangular equation such as
Symmetry is a property that helps us recognize and plot the graph of any equation. If an equation has a graph that is symmetric with respect to an axis, it means that if we folded the graph in half over that axis, the portion of the graph on one side would coincide with the portion on the other side. By performing three tests, we will see how to apply the properties of symmetry to polar equations. Further, we will use symmetry (in addition to plotting key points, zeros, and maximums of
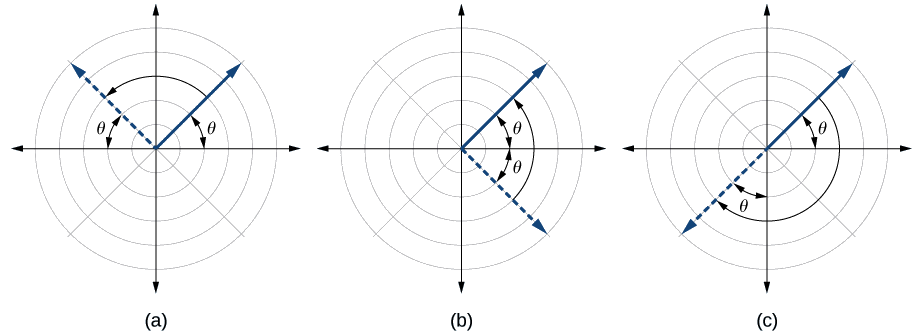
In the first test, we consider symmetry with respect to the line
This equation exhibits symmetry with respect to the line
In the second test, we consider symmetry with respect to the polar axis (
The graph of this equation exhibits symmetry with respect to the polar axis.
In the third test, we consider symmetry with respect to the pole (origin). We replace
The equation has failed the symmetry test, but that does not mean that it is not symmetric with respect to the pole. Passing one or more of the symmetry tests verifies that symmetry will be exhibited in a graph. However, failing the symmetry tests does not necessarily indicate that a graph will not be symmetric about the line
Note: SYMMETRY TESTS
A polar equation describes a curve on the polar grid. The graph of a polar equation can be evaluated for three types of symmetry, as shown in Figure
How to: Given a polar equation, test for symmetry.
- Substitute the appropriate combination of components for
- If the resulting equations are equivalent in one or more of the tests, the graph produces the expected symmetry.
Example
Test the equation
Solution
Test for each of the three types of symmetry.
|
1) Replacing |
Passed |
|
2) Replacing |
Failed |
|
3) Replacing |
Failed |
Analysis
Using a graphing calculator, we can see that the equation

Exercise
Test the equation for symmetry:
- Answer
-
The equation fails the symmetry test with respect to the line
Graphing Polar Equations by Plotting Points
To graph in the rectangular coordinate system we construct a table of
Finding Zeros and Maxima
To find the zeros of a polar equation, we solve for the values of
For many of the forms we will encounter, the maximum value of a polar equation is found by substituting those values of
Similarly, the maximum value of the sine function is
Example
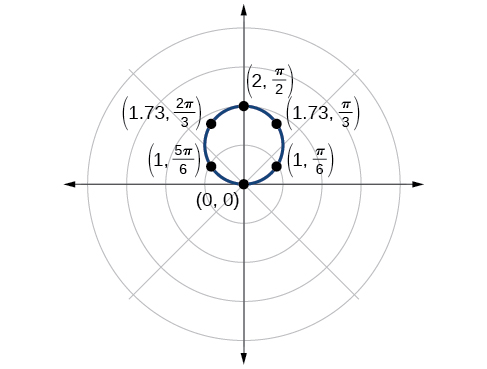
Using the equation in Example
Solution
To find the zeros, set
Substitute any one of the
The points
To find the maximum value of the equation, look at the maximum value of the trigonometric function
Analysis
The point
Exercise
Without converting to Cartesian coordinates, test the given equation for symmetry and find the zeros and maximum values of
- Answer
-
Tests will reveal symmetry about the polar axis. The zero is
Investigating Circles
Now we have seen the equation of a circle in the polar coordinate system. In the last two examples, the same equation was used to illustrate the properties of symmetry and demonstrate how to find the zeros, maximum values, and plotted points that produced the graphs. However, the circle is only one of many shapes in the set of polar curves.
There are five classic polar curves: cardioids, limaҫons, lemniscates, rose curves, and Archimedes’ spirals. We will briefly touch on the polar formulas for the circle before moving on to the classic curves and their variations.
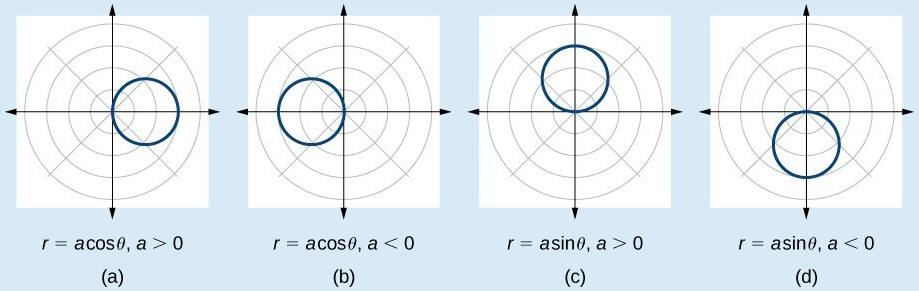
FORMULAS FOR THE EQUATION OF A CIRCLE
Some of the formulas that produce the graph of a circle in polar coordinates are given by
Example
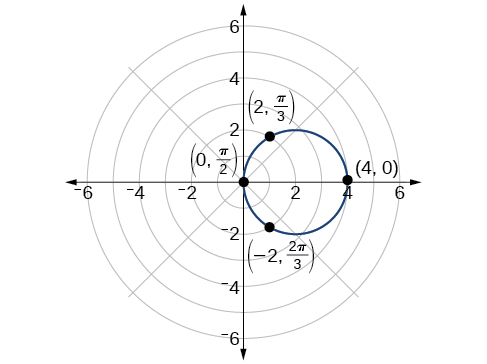
Sketch the graph of
Solution
First, testing the equation for symmetry, we find that the graph is symmetric about the polar axis. Next, we find the zeros and maximum
To find the maximum value of
The maximum value of the equation is
As
Investigating Cardioids
While translating from polar coordinates to Cartesian coordinates may seem simpler in some instances, graphing the classic curves is actually less complicated in the polar system. The next curve is called a cardioid, as it resembles a heart. This shape is often included with the family of curves called limaçons, but here we will discuss the cardioid on its own.
FORMULAS FOR A CARDIOID
The formulas that produce the graphs of a cardioid are given by
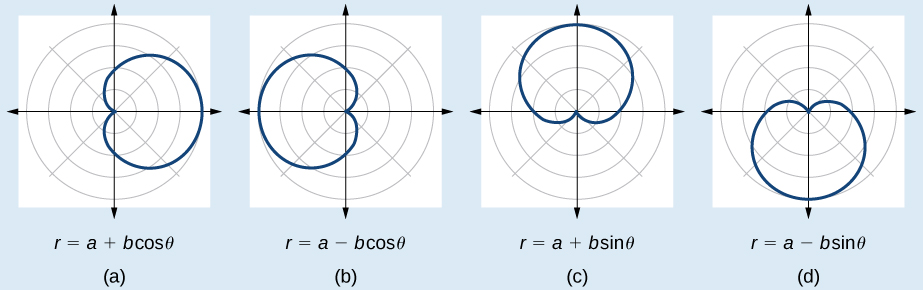
How to: Given the polar equation of a cardioid, sketch its graph
- Check equation for the three types of symmetry.
- Find the zeros. Set
- Find the maximum value of the equation according to the maximum value of the trigonometric expression.
- Make a table of values for
- Plot the points and sketch the graph.
Example
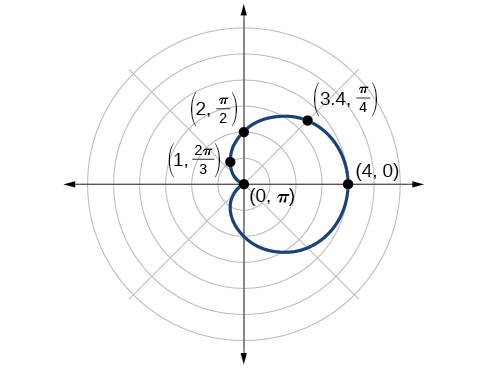
Sketch the graph of
Solution
First, testing the equation for symmetry, we find that the graph of this equation will be symmetric about the polar axis. Next, we find the zeros and maximums. Setting
The maximum value of
The point
We found that the polar equation is symmetric with respect to the polar axis, but as it extends to all four quadrants, we need to plot values over the interval
| θ | 0 | ||||
|---|---|---|---|---|---|
| r | 4 | 3.41 | 2 | 1 | 0 |
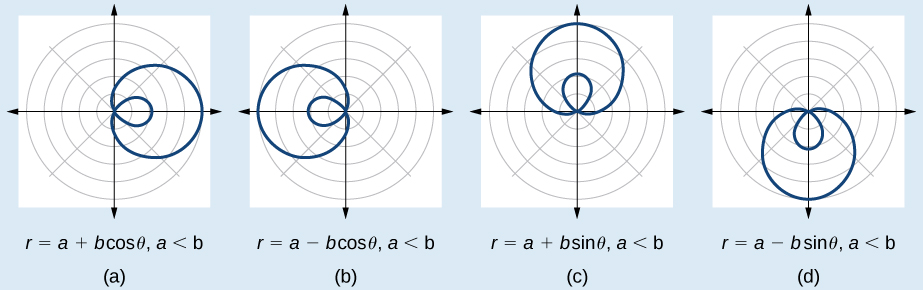
Investigating Limaçons
The word limaçon is Old French for “snail,” a name that describes the shape of the graph. As mentioned earlier, the cardioid is a member of the limaçon family, and we can see the similarities in the graphs. The other images in this category include the one-loop limaçon and the two-loop (or inner-loop) limaçon. One-loop limaçons are sometimes referred to as dimpled limaçons when
FORMULAS FOR ONE-LOOP LIMAÇONS
The formulas that produce the graph of a dimpled one-loop limaçon are given by
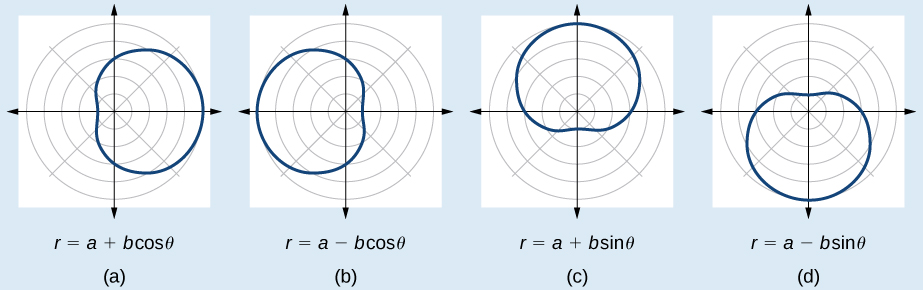
How to: Given a polar equation for a one-loop limaçon, sketch the graph
- Test the equation for symmetry. Remember that failing a symmetry test does not mean that the shape will not exhibit symmetry. Often the symmetry may reveal itself when the points are plotted.
- Find the zeros.
- Find the maximum values according to the trigonometric expression.
- Make a table.
- Plot the points and sketch the graph.
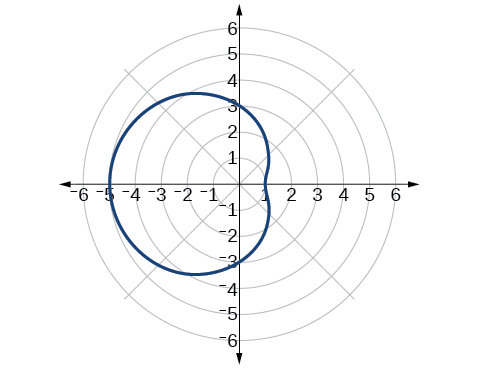
Example
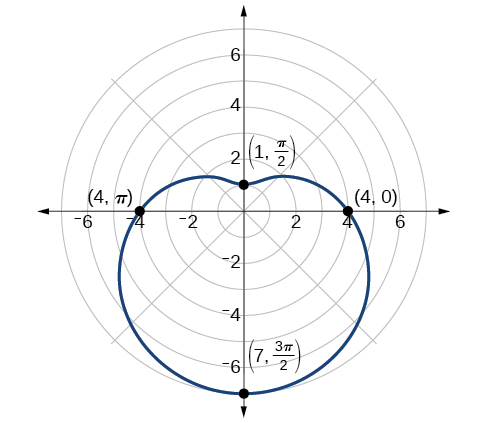
Graph the equation
Solution
First, testing the equation for symmetry, we find that it fails all three symmetry tests, meaning that the graph may or may not exhibit symmetry, so we cannot use the symmetry to help us graph it. However, this equation has a graph that clearly displays symmetry with respect to the line
Next, we find the zeros and maximum, and plot the reflecting points to verify any symmetry. Setting
So, there is at least one polar axis intercept at
Next, as the maximum value of the sine function is
Make a table of the coordinates similar to Table
The graph is shown in Figure
Analysis
This is an example of a curve for which making a table of values is critical to producing an accurate graph. The symmetry tests fail; the zero is undefined. While it may be apparent that an equation involving
Exercise
Sketch the graph of
- Answer
-
Figure
Another type of limaçon, the inner-loop limaçon, is named for the loop formed inside the general limaçon shape. It was discovered by the German artist Albrecht Dürer(1471-1528), who revealed a method for drawing the inner-loop limaçon in his 1525 book Underweysung der Messing. A century later, the father of mathematician Blaise Pascal, Étienne Pascal(1588-1651), rediscovered it.
FORMULAS FOR INNER-LOOP LIMAÇONS
The formulas that generate the inner-loop limaçons are given by
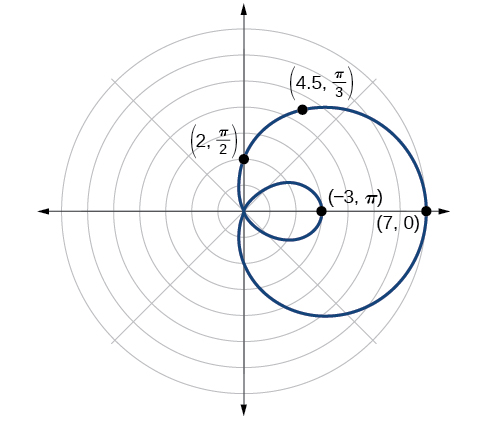
Example
Sketch the graph of
Solution
Testing for symmetry, we find that the graph of the equation is symmetric about the polar axis. Next, finding the zeros reveals that when
Even though we have found symmetry, the zero, and the maximum, plotting more points will help to define the shape, and then a pattern will emerge. See Table
As expected, the values begin to repeat after
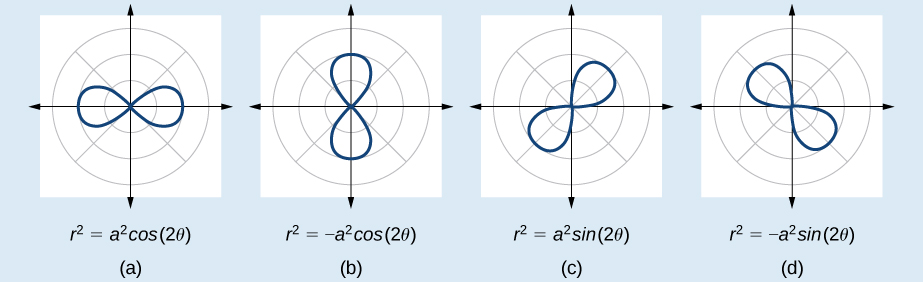
Investigating Lemniscates
The lemniscate is a polar curve resembling the infinity symbol
FORMULAS FOR LEMNISCATES
The formulas that generate the graph of a lemniscate are given by
Example
Sketch the graph of
Solution
The equation exhibits symmetry with respect to the line
Let’s find the zeros. It should be routine by now, but we will approach this equation a little differently by making the substitution
So, the point
Now let’s find the maximum value. Since the maximum of
We have a maximum at
Make a table similar to Table
Plot the points on the graph, such as the one shown in Figure
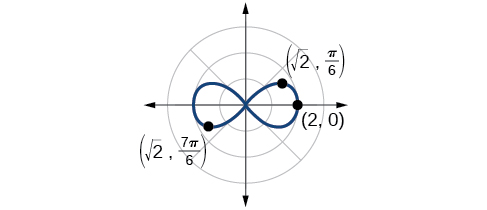
Analysis
Making a substitution such as
Some of the points on this graph may not show up using the Trace function on the TI-84 graphing calculator, and the calculator table may show an error for these same points of
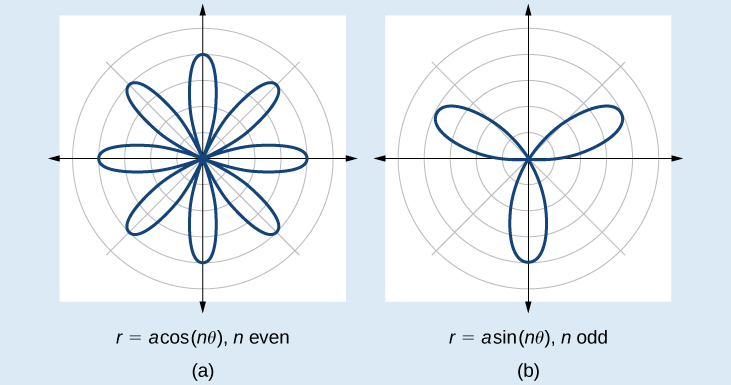
Investigating Rose Curves
The next type of polar equation produces a petal-like shape called a rose curve. Although the graphs look complex, a simple polar equation generates the pattern.
ROSE CURVES
The formulas that generate the graph of a rose curve are given by
Example
Sketch the graph of
Solution
Testing for symmetry, we find again that the symmetry tests do not tell the whole story. The graph is not only symmetric with respect to the polar axis, but also with respect to the line
Now we will find the zeros. First make the substitution
The zero is
Next, we find the maximum
The point
The graph of the rose curve has unique properties, which are revealed in Table
As
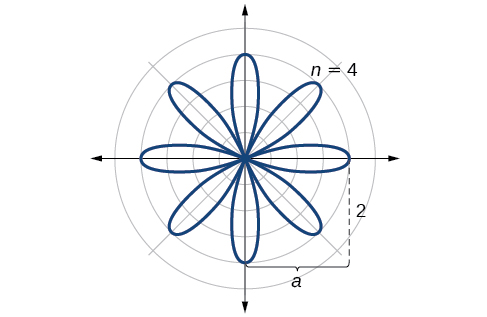
Analysis
When these curves are drawn, it is best to plot the points in order, as in the Table
Exercise
Sketch the graph of
- Answer
-
The graph is a rose curve,
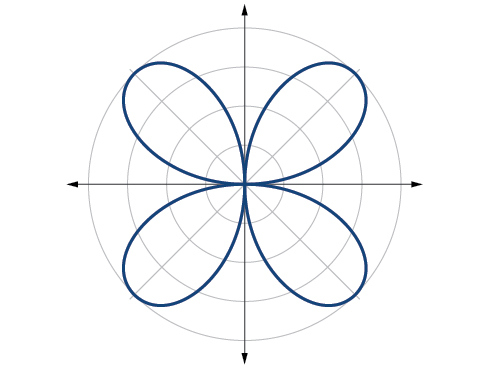
Figure
Example
Sketch the graph of
Solution
The graph of the equation shows symmetry with respect to the line
The maximum value is calculated at the angle where
Thus, the maximum value of the polar equation is
Create a table of values similar to Table
| \(0\0 |
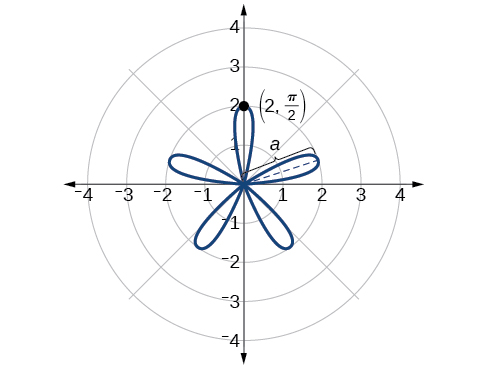
Exercise
Sketch the graph of
- Answer
-
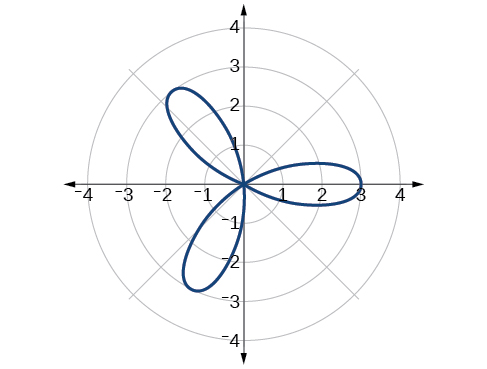
Figure Rose curve,
Investigating the Archimedes’ Spiral
The final polar equation we will discuss is the Archimedes’ spiral, named for its discoverer, the Greek mathematician Archimedes (c. 287 BCE - c. 212 BCE), who is credited with numerous discoveries in the fields of geometry and mechanics.
ARCHIMEDES’ SPIRAL
The formula that generates the graph of the Archimedes’ spiral is given by
![Two graphs side by side of Archimedes' spiral. (A) is r= theta, [0, 2pi]. (B) is r=theta, [0, 4pi]. Both start at origin and spiral out counterclockwise. The second has two spirals out while the first has one.](https://math.libretexts.org/@api/deki/files/7445/CNX_Precalc_Figure_08_04_020new.jpg?revision=1)
How to: Given an Archimedes’ spiral over
- Make a table of values for
- Plot the points and sketch the graph.
Example
Sketch the graph of
Solution
As
Create a table such as Table
Notice that the r-values are just the decimal form of the angle measured in radians. We can see them on a graph in Figure
![Graph of Archimedes' spiral r=theta over [0,2pi]. Starts at origin and spirals out in one loop counterclockwise. Points (pi/4, pi/4), (pi/2,pi/2), (pi,pi), (5pi/4, 5pi/4), (7pi/4, pi/4), and (2pi, 2pi) are marked.](https://math.libretexts.org/@api/deki/files/7446/CNX_Precalc_Figure_08_04_021F.jpg?revision=1)
Analysis
The domain of this polar curve is
Exercise
Sketch the graph of
- Answer
-
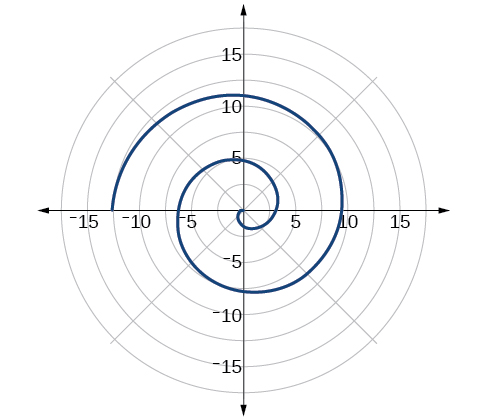
Figure
Summary of Curves
We have explored a number of seemingly complex polar curves in this section. Figure


Extra Practice
- For the following exercises, test each equation for symmetry.
- Sketch a graph of the polar equation
- Sketch a graph of the polar equation
- Sketch a graph of the polar equation
Key Concepts
- It is easier to graph polar equations if we can test the equations for symmetry with respect to the line
- There are three symmetry tests that indicate whether the graph of a polar equation will exhibit symmetry. If an equation fails a symmetry test, the graph may or may not exhibit symmetry. See Example
- Polar equations may be graphed by making a table of values for
- The maximum value of a polar equation is found by substituting the value
- The zeros of a polar equation are found by setting
- Some formulas that produce the graph of a circle in polar coordinates are given by
- The formulas that produce the graphs of a cardioid are given by
- The formulas that produce the graphs of a one-loop limaçon are given by
- The formulas that produce the graphs of an inner-loop limaçon are given by
- The formulas that produce the graphs of a lemniscates are given by
- The formulas that produce the graphs of rose curves are given by
- The formula that produces the graph of an Archimedes’ spiral is given by
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.

