6.3: Converting Between Systems

Learning Objectives

• Convert rectangular coordinates to polar coordinates.
• Convert equations given in rectangular form to equations in polar form and vise versa.

Transforming Equations between Polar and Rectangular Forms

We can now convert coordinates between polar and rectangular form. Converting equations can be more difficult, but it can be beneficial to be able to convert between the two forms. Since there are a number of polar equations that cannot be expressed clearly in Cartesian form, and vice versa, we can use the same procedures we used to convert points between the coordinate systems. We can then use a graphing calculator to graph either the rectangular form or the polar form of the equation.

How to: Given an equation in polar form, graph it using a graphing calculator

1. Change the MODE to POL, representing polar form.
2. Press the Y= button to bring up a screen allowing the input of six equations: $r_1$, $r_2$,..., $r_6$.
3. Enter the polar equation, set equal to $r$.
4. Press GRAPH.

Example $\PageIndex{1A}$: Writing a Cartesian Equation in Polar Form

Write the Cartesian equation $x^2+y^2=9$ in polar form.

Solution

The goal is to eliminate $x$ and $y$ from the equation and introduce $r$ and $\theta$. Ideally, we would write the equation $r$ as a function of $\theta$. To obtain the polar form, we will use the relationships between $(x,y)$ and $(r,\theta)$. Since $x=r \cos \theta$ and $y=r \sin \theta$, we can substitute and solve for $r$.

$$\begin{align*} {(r \cos \theta)}^2+{(r \sin \theta)}^2 &= 9 \\[4pt] r^2 {\cos}^2 \theta + r^2 {\sin}^2 \theta &= 9 \\[4pt] r^2({\cos}^2 \theta + {\sin}^2 \theta) &= 9 \\[4pt] r^2(1) &= 9 && \text {Substitute } {\cos}^2 \theta+{\sin}^2 \theta=1\\[4pt] r &= \pm 3 && \text {Use the square root property.} \end{align*}$$

Thus, $x^2+y^2=9$, $r=3$, and $r=−3$ should generate the same graph. See Figure $\PageIndex{1}$.

Figure $\PageIndex{1}$: (a) Cartesian form $x^2+y^2=9$ (b) Polar form $r=3$

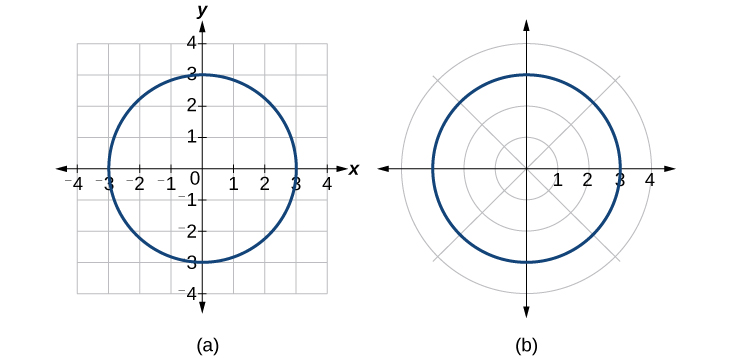
To graph a circle in rectangular form, we must first solve for $y$.

$$\begin{align*} x^2+y^2&= 9\\ y^2&= 9-x^2\\ y&= \pm \sqrt{9-x^2} \end{align*}$$

Note that this is two separate functions, since a circle fails the vertical line test. Therefore, we need to enter the positive and negative square roots into the calculator separately, as two equations in the form $Y_1=\sqrt{9−x^2}$ and $Y_2=−\sqrt{9−x^2}$. Press GRAPH.

Example $\PageIndex{1B}$: Rewriting a Cartesian Equation as a Polar Equation

Rewrite the Cartesian equation $x^2+y^2=6y$ as a polar equation.

Solution

This equation appears similar to the previous example, but it requires different steps to convert the equation.

We can still follow the same procedures we have already learned and make the following substitutions:

$\begin{array}{ll} r^2=6y & \text{Use }x^2+y^2=r^2. \\ r^2=6r \sin \theta & \text{Substitute }y=r \sin \theta. \\ r^2−6r \sin \theta=0 & \text{Set equal to }0. \\ r(r−6 \sin \theta)=0 & \text{Factor and solve.} \\ r=0 & \text{We reject }r=0 \text{, as it only represents one point, }(0,0). \\ \text{or }r=6 \sin \theta \end{array}$

Therefore, the equations $x^2+y^2=6y$ and $r=6 \sin \theta$ should give us the same graph. See Figure $\PageIndex{2}$.

Figure $\PageIndex{2}$: (a) Cartesian form $x^2+y^2=6y$ (b) polar form $r=6 \sin \theta$

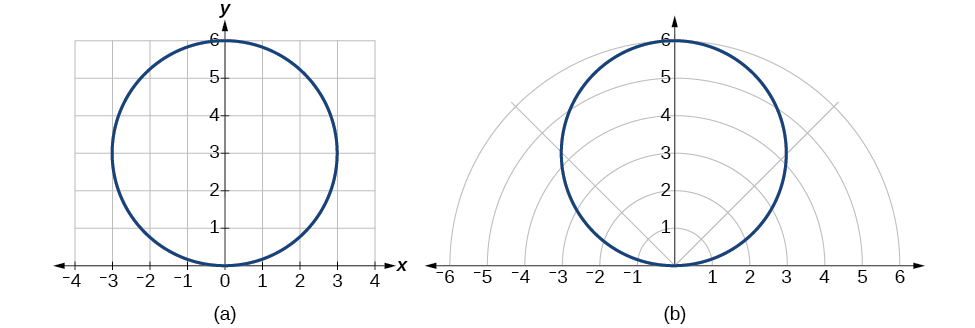
The Cartesian or rectangular equation is plotted on the rectangular grid, and the polar equation is plotted on the polar grid. Clearly, the graphs are identical.

Exercise $\PageIndex{1A}$: Rewriting a Cartesian Equation in Polar Form

Rewrite the Cartesian equation $y=3x+2$ as a polar equation.

Answer

We will use the relationships $x=r \cos \theta$ and $y=r \sin \theta$.

$$\begin{align*} y &=3x+2 \\[4pt] r \sin \theta &= 3r \cos \theta + 2 \\[4pt] r \sin \theta−3r \cos \theta &=2 \\[4pt] r(\sin \theta−3 \cos \theta) &=2 && \text{Isolate }r. \\[4pt] r&=\dfrac{2}{\sin \theta−3\cos \theta} && \text{Solve for }r. \end{align*}$$

Exercise $\PageIndex{1B}$:

Rewrite the Cartesian equation $y^2=3−x^2$ in polar form.

Answer

$r=\sqrt{3}$

Identify and Graph Polar Equations by Converting to Rectangular Equations

We have learned how to convert rectangular coordinates to polar coordinates, and we have seen that the points are indeed the same. We have also transformed polar equations to rectangular equations and vice versa. Now we will demonstrate that their graphs, while drawn on different grids, are identical.

Example $\PageIndex{2A}$: Graphing a Polar Equation by Converting to a Rectangular Equation

Covert the polar equation $r=2 \sec \theta$ to a rectangular equation, and draw its corresponding graph.

Solution

The conversion is

$$\begin{align*} r &=2 \sec \theta \\ r &= \dfrac{2}{\cos \theta} \\ r \cos \theta &=2 \\ x &=2 \end{align*}$$

Notice that the equation $r=2 \sec \theta$ drawn on the polar grid is clearly the same as the vertical line $x=2$ drawn on the rectangular grid (see Figure $\PageIndex{14}$). Just as $x=c$ is the standard form for a vertical line in rectangular form, $r=c \sec \theta$ is the standard form for a vertical line in polar form.

Figure $\PageIndex{3}$: (a) Polar grid (b) Rectangular coordinate system

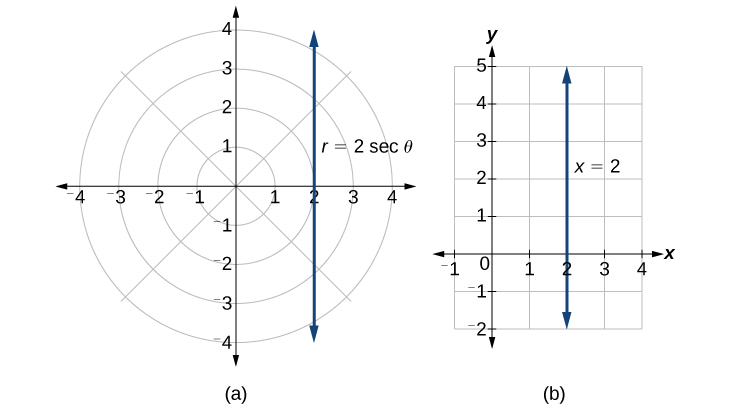
A similar discussion would demonstrate that the graph of the function $r=2 \csc \theta$ will be the horizontal line $y=2$. In fact, $r=c \csc \theta$ is the standard form for a horizontal line in polar form, corresponding to the rectangular form $y=c$.

Example $\PageIndex{2B}$: Rewriting a Polar Equation in Cartesian Form

Rewrite the polar equation $r=\dfrac{3}{1−2 \cos \theta}$ as a Cartesian equation.

Solution

The goal is to eliminate $\theta$ and $r$, and introduce $x$ and $y$. We clear the fraction, and then use substitution. To replace $r$ with $x$ and $y$, we must use the expression $x^2+y^2=r^2$.

$$\begin{align*} r &=\dfrac{3}{1−2 \cos \theta} \\[4pt] r(1−2 \cos \theta) &=3 \\[4pt] r\left(1−2\left(\dfrac{x}{r}\right)\right) &=3 && \text{Use }\cos \theta=\dfrac{x}{r} \text{ to eliminate }\theta. \\[4pt] r−2x &=3 \\[4pt] r &=3+2x && \text{Isolate }r. \\[4pt] r^2 &={(3+2x)}^2 && \text{Square both sides.} \\[4pt] x^2+y^2 &={(3+2x)}^2 && \text{Use }x^2+y^2=r^2. \end{align*}$$

The Cartesian equation is $x^2+y^2={(3+2x)}^2$. However, to graph it, especially using a graphing calculator or computer program, we want to isolate $y$.

$$\begin{align*} x^2+y^2 &= {(3+2x)}^2 \\ y^2 &= {(3+2x)}^2-x^2 \\ y &= \pm \sqrt{{(3+2x)}^2-x^2} \end{align*}$$

When our entire equation has been changed from $r$ and $\theta$ to $x$ and $y$, we can stop, unless asked to solve for $y$ or simplify. See Figure $\PageIndex{4}$.

Figure $\PageIndex{4}$

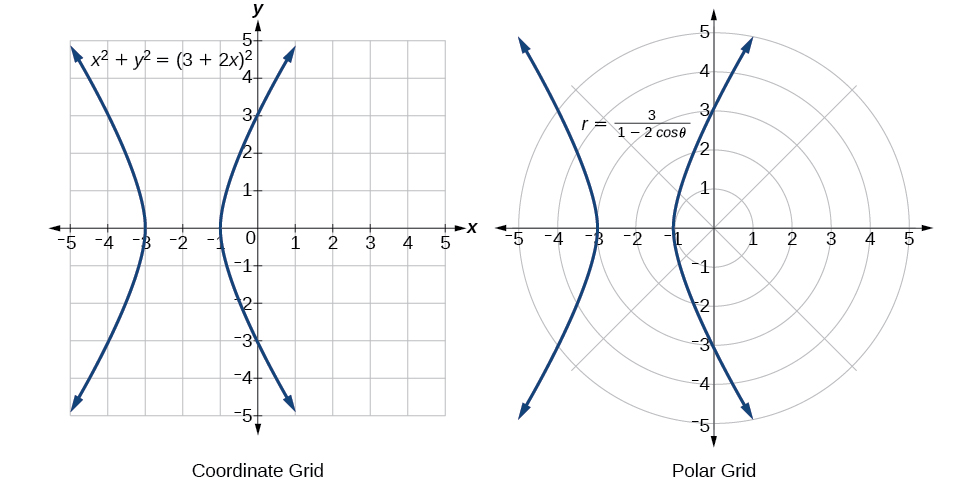
The “hour-glass” shape of the graph is called a hyperbola. Hyperbolas have many interesting geometric features and applications, which we will investigate further in Analytic Geometry.

Analysis

In this example, the right side of the equation can be expanded and the equation simplified further, as shown above. However, the equation cannot be written as a single function in Cartesian form. We may wish to write the rectangular equation in the hyperbola’s standard form. To do this, we can start with the initial equation.

$$\begin{align*} x^2+y^2 &= {(3+2x)}^2 \\[4pt] x^2+y^2−{(3+2x)}^2 &=0 \\[4pt] x^2+y^2−(9+12x+4x^2) &=0 \\[4pt] x^2+y^2−9−12x−4x^2 &=0 \\ −3x^2−12x+y^2 &=9 && \text{Multiply through by }−1. \\[4pt] 3x^2+12x−y^2 &= −9 \\[4pt] 3(x^2+4x)−y^2 &=−9 && \text{Organize terms to complete the square for }x. \\[4pt] 3(x^2+4x+4)−y^2 &= −9+12 \\[4pt] 3{(x+2)}^2−y^2 &=3 \\[4pt] {(x+2)}^2−\dfrac{y^2}{3} &=1 \end{align*}$$

Exercise $\PageIndex{2}$

Rewrite the polar equation $r=2 \sin \theta$ in Cartesian form.

Answer

$x^2+y^2=2y$ or, in the standard form for a circle, $x^2+{(y−1)}^2=1$

Example $\PageIndex{3}$: Rewriting a Polar Equation in Cartesian Form

Rewrite the polar equation $r=\sin(2\theta)$ in Cartesian form.

Solution

$$\begin{aligned} r &=\sin(2\theta) && \text{Use the double angle identity for sine.} \\[4pt] r &=2 \sin \theta \cos \theta && \text{Use }\cos \theta=\dfrac{x}{r} \text{ and } \sin \theta =\dfrac{y}{r}. \\ r&=2 \left(\dfrac{x}{r}\right)\left(\dfrac{y}{r}\right) && \text{ Simplify.} \\[4pt] r &= \dfrac{2xy}{r^2} && \text{Multiply both sides by }r^2. \\[4pt] r^3 &=2xy \\[4pt] {(x^2+y^2)}^3 &=2xy && \text{As }x^2+y^2 =r^2, r=\sqrt{x^2+y^2}. \end{aligned}$$

This equation can also be written as

${(x^2+y^2)}^{\frac{3}{2}}=2xy \text{ or }x^2+y^2={(2xy)}^{\frac{2}{3}}$

Extra Practice

For the following exercises, convert the given Cartesian equation to a polar equation.

1. $x=-2$
2. $x^{2}+y^{2}=64$
3. $x^{2}+y^{2}=-2 y$

For the following exercises, convert the given polar equation to a Cartesian equation.

1. $r=7 \cos \theta$
2. $r=\frac{-2}{4 \cos \theta+\sin \theta}$

For the following exercises, convert to rectangular form and graph.

1. $\theta=\frac{3 \pi}{4}$
2. $r=5 \sec \theta$

Key Equations

Conversion formulas

$\cos \theta=\dfrac{x}{r} \rightarrow x=r \cos\theta$ $\sin \theta=\dfrac{y}{r} \rightarrow y=r \sin \theta$ $r^2=x^2+y^2$ $\tan \theta=\dfrac{y}{x}$

Key Concepts

• Transforming equations between polar and rectangular forms means making the appropriate substitutions based on the available formulas, together with algebraic manipulations. See Example $\PageIndex{1}$.
• Using the appropriate substitutions makes it possible to rewrite a polar equation as a rectangular equation, and then graph it in the rectangular plane. See Example $\PageIndex{2}$ and Example $\PageIndex{3}$.

Contributors and Attributions

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.