5.2: Area of a Triangle

Last updated
Save as PDF

Page ID: 61266

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Apply the area formula to triangles where you know two sides and the included angle.
Apply the area formula to triangles where you know all three sides, Heron’s Formula.
Use the area formulas in real-world and applied problems.

Area of a Triangle

We will now develop a few different ways to calculate the area of a triangle. Perhaps the most familiar formula for the area is the following:

The triangles in Figure $\PageIndex{1}$ illustrate the use of the variables in this formula.

The area $A$ of a triangle is \[A = \dfrac{1}{2}bh.\]

where $b$ is the length of the base of a triangle and $h$ is the length of the altitude that is perpendicular to that base.

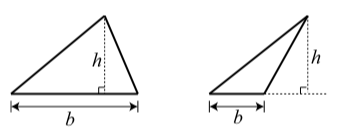
$3.19.png$

Figure $\PageIndex{1}$: Diagrams for the Formula for the Area of a Triangle

Exercise $\PageIndex{1}$

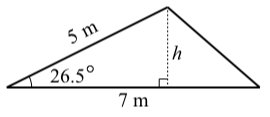
$pc3.21.png$

Suppose that the length of two sides of a triangle are $5$ meters and $7$ meters and that the angle formed by these two sides is $26.5^\circ$. See the diagram on the right.

For this problem, we are using the side of length $7$ meters as the base. The altitude of length $h$ that is perpendicular to this side is shown.

Use right triangle trigonometry to determine the value of $h$.
Determine the area of this triangle.

Answer

Using the right triangle, we see that $\sin(26.5^\circ) = \dfrac{h}{5}$. So $h = 5\sin(26.5^\circ)$, and the area of the triangle is

\[A = \dfrac{1}{2}(7)[5\sin(26.5^\circ)] = \dfrac{35}{2}\sin(26.5^\circ) \approx 7.8085\]

The area of the triangle is approximately $7.8085$ square meters.

If we know the length of two sides of a triangle and the angle formed by these two sides, then we can determine the area of that triangle.

The Area of a Triangle

The area of a triangle equals one-half the product of two of its sides times the sine of the angle formed by these two sides.

Exercise $\PageIndex{2}$

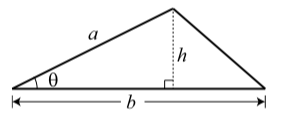
$pc3.22.png$

In the diagram on the right, $b$ is the length of the base of a triangle, $a$ is the length of another side, and $\theta$ is the angle formed by these two sides. We let $A$ be the area of the triangle.

Prove that \[A = \dfrac{1}{2}ab\sin(\theta)\]

Explain why this proves the formula for the area of a triangle.

Answer: Using the right triangle, we see that $\sin(\theta) = \dfrac{h}{a}$. So $h = a\sin(\theta)$, and the area of the triangle is \[A = \dfrac{1}{2}b(a\sin(\theta)) = \dfrac{1}{2}ab\sin(\theta)\]

Example $\PageIndex{1}$: Finding the Area of an Oblique Triangle

Find the area of a triangle with sides $a=90$, $b=52$, and angle $\gamma=102°$. Round the area to the nearest integer.

Solution

Using the formula, we have

\[\begin{align*} Area&= \dfrac{1}{2}ab \sin \gamma\\ Area&= \dfrac{1}{2}(90)(52) \sin(102^{\circ})\\ Area&\approx 2289\; \text{square units} \end{align*}\]

Exercise $\PageIndex{3}$

Find the area of the triangle given $\beta=42°$, $a=7.2 ft$, $c=3.4 ft$. Round the area to the nearest tenth.

Answer: about $8.2$ square feet

There is another common formula for the area of a triangle known as Heron’s Formula named after Heron of Alexandria (circa 75 CE). This formula shows that the area of a triangle can be computed if the lengths of the three sides of the triangle are known.

Heron’s Formula

The area $A$ of a triangle with sides of length $a$, $b$, and $c$ is given by the formula

\[A = \sqrt{s(s - a)(s - b)(s - c)} \label{Heron}\]

where $s = \dfrac{1}{2}(a+ b + c)$.

For example, suppose that the lengths of the three sides of a triangle are $a = 3ft$, $b = 5ft$, and $c = 6ft$. Using Heron’s Formula (Equation \ref{Heron}), we get

\[s = \dfrac{1}{2}(a+ b + c)\]

\[s = 7\]

\[A = \sqrt{s(s - a)(s - b)(s - c)}\]

\[A = \sqrt{7(7 - 3)(7 - 5)(7 - 6)}\]

\[A = \sqrt{42}\]

This fairly complex formula is actually derived from the previous formula for the area of a triangle and the Law of Cosines. We begin our exploration of the proof of this formula in Progress Check

Exercise $\PageIndex{4}$

Suppose we have a triangle as shown in the diagram below.

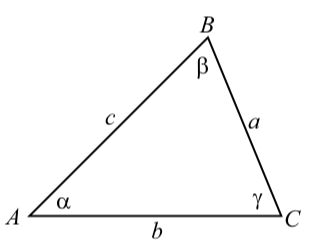
$pc3.23.png$

Use the Law of Cosines that involves the angle $\gamma$ and solve this formula for $\cos(\gamma)$. This gives a formula for $\cos(\gamma)$ in terms of $a$, $b$, and $c$.
Use the Pythagorean Identity $\cos^{2}(\gamma) + \sin^{2}(\gamma) = 1$ 1 to write $\sin(\gamma)$ in terms of $\cos^{2}(\gamma)$. Substitute for $\cos^{2}(\gamma)$ using the formula in (1). This gives a formula for $\sin(\gamma)$ in terms of $a$, $b$, and $c$. (Do not do any algebraic simplification.)
We also know that a formula for the area of this triangle is $A = \dfrac{1}{2}ab\sin(\gamma)$

Substitute for $\sin(\gamma)$ using the formula in (2). (Do not do any algebraic simplification.) This gives a formula for the area $A$ in terms of $a$, $b$, and $c$.

The formula obtained in Progress Check 3.23 was \[A = \dfrac{1}{2}ab\sqrt{1 - (\dfrac{a^{2} + b^{2} - c^{2}}{2ab})^{2}}\]

This is a formula for the area of a triangle in terms of the lengths of the three sides of the triangle. It does not look like Heron’s Formula, but we can use some substantial algebra to rewrite this formula to obtain Heron’s Formula. This algebraic work is completed in the appendix for this section.

Answer

1. Using the Law of Cosines, we see that \[c^{2} = a^{2} + b^{2} - 2ab\cos(\gamma)\] \[2ab\cos(\gamma) = a^{2} + b^{2} - c^{2}\] \[\cos(\gamma) = \dfrac{a^{2} + b^{2} - c^{2}}{2ab}\]

2. We see that

\[\sin^{2}(\gamma) = 1 - \cos^{2}(\gamma).\]

Since $\gamma$ is between $0^\circ$ and $180^\circ$, we know that $\sin(\gamma) > 0$ and so

\[\sin(\gamma) = \sqrt{1-(\dfrac{a^{2} + b^{2} - c^{2}}{2ab})^{2}}\]

3. Substituting the equation in part (2) into the formula $A = \dfrac{1}{2}ab\sin(\gamma)$, we obtain

\[A = \dfrac{1}{2}ab\sin(\gamma) = \dfrac{1}{2}ab\sqrt{1 - (\dfrac{a^{2} + b^{2} - c^{2}}{2ab})^{2}}\]

Appendix – Proof of Heron’s Formula

The formula for the area of a triangle obtained in Progress Check 3.23 was \[A = \dfrac{1}{2}ab\sqrt{1 - (\dfrac{a^{2} + b^{2} - c^{2}}{2ab})^{2}}\]

We now complete the algebra to show that this is equivalent to Heron’s formula. The first step is to rewrite the part under the square root sign as a single fraction.

\[A = \dfrac{1}{2}ab\sqrt{1 - (\dfrac{a^{2} + b^{2} - c^{2}}{2ab})^{2}}\]

\[= \dfrac{1}{2}ab\sqrt{\dfrac{(2ab)^{2} - (a^{2} + b^{2} - c^{2})^{2}}{(2ab)^{2}}}\]

\[= \dfrac{1}{2}ab\dfrac{\sqrt{(2ab)^{2} - (a^{2} + b^{2} - c^{2})^{2}}}{2ab}\]

\[= \dfrac{\sqrt{(2ab)^{2} - (a^{2} + b^{2} - c^{2})^{2}}}{4}\]

Squaring both sides of the last equation, we obtain \[A^{2} = \dfrac{(2ab)^{2} - (a^{2} + b^{2} - c^{2})^{2}}{16}\]

The numerator on the right side of the last equation is a difference of squares. We will now use the difference of squares formula, $x^{2} - y^{2} = (x - y)(x + y)$ to factor the numerator.

\[A^{2} = \dfrac{(2ab)^{2} - (a^{2} + b^{2} - c^{2})^{2}}{16}\]

\[= \dfrac{(2ab - (a^{2} + b^{2} - c^{2}))(2ab + (a^{2} + b^{2} - c^{2}))}{16}\]

\[= \dfrac{(-a^{2} + 2ab - b^{2} + c^{2})(a^{2} + 2ab + b^{2} - c^{2})}{16}\]

We now notice that $-a^{2} + 2ab - b^{2} = -(a - b)^{2}$ and $a^{2} + 2ab + b^{2} = (a + b)^{2}$. So using these in the last equation, we have

\[A^{2} = \dfrac{(-(a - b)^{2} + c^{2})((a + b)^{2} - c^{2})}{16}\]

\[= \dfrac{(-[(a - b)^{2} - c^{2}])((a + b)^{2} - c^{2})}{16}\]

We can once again use the difference of squares formula as follows:

\[(a - b)^{2} - c^{2} = (a - b - c)(a - b + c)\]

\[(a + b)^{2} - c^{2} = (a + b - c)(a + b + c)\]

Substituting this information into the last equation for $A^{2}$, we obtain \[A^{2} = \dfrac{-(a - b - c)(a - b + c)(a + b - c)(a + b + c)}{16}\]

Since $s = \dfrac{1}{2}(a + b + c)$, $2s = a + b + c$ Now notice that

\[-(a - b - c) = -a + b + c = a + b + c - 2a = 2s - 2a\]

\[a - b + c = a + b + c -2b = 2s - 2b\]

\[a + b + c = a + b + c -2c = 2s - 2c\]

\[a + b + c = 2s\]

\[A^{2} = \dfrac{-(a - b - c)(a - b + c)(a + b - c)(a + b + c)}{16}\]
\[= \dfrac{(2s - 2a)(2s - 2b)(2s - 2c)(2s)}{16}\]
\[= \dfrac{16s(s - a)(s - b)(s - c)}{16}\]
\[= s(s - a)(s - b)(s - c)\]
\[A = \sqrt{s(s - a)(s - b)(s - c)}\]

This completes the proof of Heron’s formula.

Summary

In this section, we studied the following important concepts and ideas:

Three ways to determine the area $A$ of a triangle.

$A = \dfrac{1}{2}bh$, where $b$ is the length of the base and $h$ is the length of the altitude.

$A = \dfrac{1}{2}ab\sin(\theta)$, where $a$ and $b$ are the lengths of two sides of the triangle and $\theta$ is the angle formed by the sides of length $a$ and $b$.

Heron’s Formula. If $a$, $b$, and $c$ are the lengths of the sides of a triangle and $s = \dfrac{1}{2}(a + b + c)$, then \[A = \sqrt{s(s - a)(s - b)(s - c)}.\]