13.3: Automata, Finite-State Machines
- Last updated
- Sep 29, 2021
- Save as PDF
- Page ID
- 86187
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we will introduce the concept of an abstract machine. The machines we will examine will (in theory) be capable of performing many of the tasks associated with digital computers. One such task is solving the recognition problem for a language. We will concentrate on one class of machines, finite-state machines (finite automata). And we will see that they are precisely the machines that are capable of recognizing strings in a regular grammar.
Given an alphabet
The typical abstract machine includes an input device, the read head, which is capable of reading the symbol from the segment of the input tape that is currently in the read head. Some more advanced machines have a read/write head that can also write symbols onto the tape. The movement of the input tape after reading a symbol depends on the machine. With a finite-state machine, the next segment of the input tape is always moved into the read head after a symbol has been read. Most machines (including finite-state machines) also have a separate output tape that is written on with a write head. The output symbols come from an output alphabet,
Definition
A finite-state machine is defined by a quintet
Example
Many mechanical devices, such as simple vending machines, can be thought of as finite-state machines. For simplicity, assume that a vending machine dispenses packets of gum, spearmint (S), peppermint (P), and bubble (B), for
and the state set to be
Example
The following machine is called a parity checker. It recognizes whether or not a string in
The input alphabet is
Note how the value of the most recent output at any time is an indication of the current state of the machine. Therefore, if we start in the even state and read any finite input tape, the last output corresponds to the final state of the parity checker and tells us the parity of the string on the input tape. For example, if the string 11001010 is read from left to right, the output tape, also from left to right, will be 10001100. Since the last character is a 0, we know that the input string has even parity.
An alternate method for defining a finite-state machine is with a transition diagram. A transition diagram is a directed graph that contains a node for each state and edges that indicate the transition and output functions. An edge
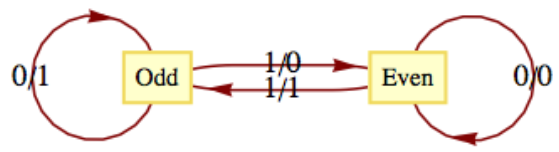 Figure
Figure One of the most significant features of a finite-state machine is that it retains no information about its past states that can be accessed by the machine itself. For example, after we input a tape encoded with the symbols 01101010 into the parity checker, the current state will be even, but we have no indication within the machine whether or not it has always been in even state. Note how the output tape is not considered part of the machine's memory. In this case, the output tape does contain a “history” of the parity checker's past states. We assume that the finite-state machine has no way of recovering the output sequence for later use.
Example
Consider the following simplified version of the game of baseball. To be precise, this machine describes one half-inning of a simplified baseball game. Suppose that in addition to home plate, there is only one base instead of the usual three bases. Also, assume that there are only two outs per inning instead of the usual three. Our input alphabet will consist of the types of hits that the batter could have: out (O), double play (DP), single (S), and home run (HR). The input DP is meant to represent a batted ball that would result in a double play (two outs), if possible. The input DP can then occur at any time. The output alphabet is the numbers 0, 1, and 2 for the number of runs that can be scored as a result of any input. The state set contains the current situation in the inning, the number of outs, and whether a base runner is currently on the base. The list of possible states is then 00 (for 0 outs and 0 runners), 01, 10, 11, and end (when the half-inning is over). The transition diagram for this machine appears in Figure
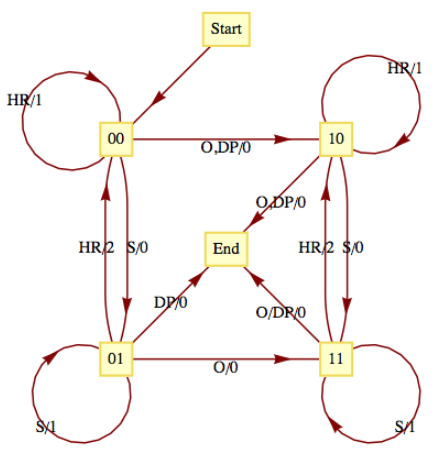 Figure
Figure Let's concentrate on one state. If the current state is 01, 0 outs and 1 runner on base, each input results in a different combination of output and next-state. If the batter hits the ball poorly (a double play) the output is zero runs and the inning is over (the limit of two outs has been made). A simple out also results in an output of 0 runs and the next state is 11, one out and one runner on base. If the batter hits a single, one run scores (output = 1) while the state remains 01. If a home run is hit, two runs are scored (output = 2) and the next state is 00. If we had allowed three outs per inning, this graph would only be marginally more complicated. The usual game with three bases would be quite a bit more complicated, however.
Example
As we mentioned at the outset of this section, finite-state machines can recognize strings in a regular language. Consider the language
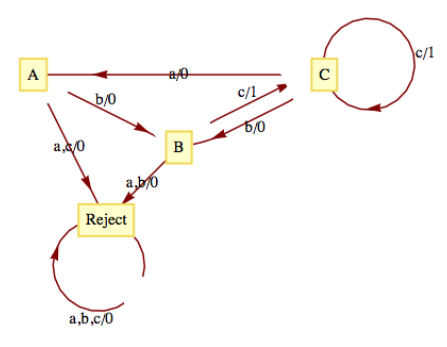 Figure
Figure The construction of this machine is quite easy: note how each production rule translates into an edge between states other than Reject. For example,
A finite-state machine can be designed to add positive integers of any size. Given two integers in binary form,
Notice the special input 111 at the end. All possible inputs except the last one must even parity (contain an even number of ones). The output sequence is the sum of
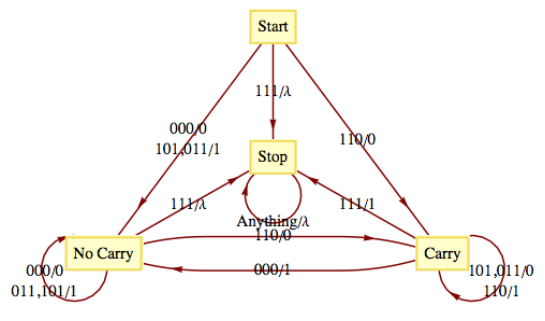 Figure
Figure 14.3.1: Exercises
Exercise
Draw a transition diagram for the vending machine described in Example
- Answer
-
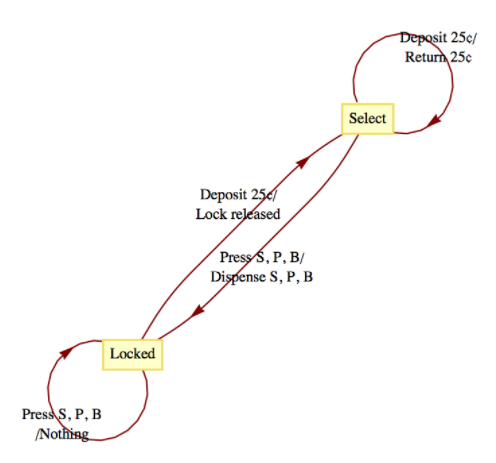 Figure
Figure
Exercise
Construct finite-state machines that recognize the regular languages that you identified in Section 14.2.
Exercise
What is the input set for the binary adding machine in Example
- Answer
-
Exercise
What input sequence would be used to compute the sum of 1101 and 0111 (binary integers)? What would the output sequence be?
Exercise
The Gray Code Decoder. The finite-state machine defined by the following figure has an interesting connection with the Gray Code.
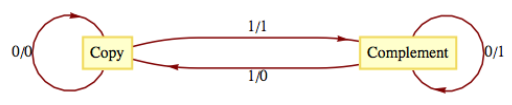 Figure
Figure Given a string
- In what positions
- Prove that the Gray Code Decoder always works.
- Answer
-
-
- Input: 10110, Output: 11011
- Input: 00100, Output: 00111
- Input:11111, Output: 10101
- Input: 10110, Output: 11011
- Let
If
If
-


