12.4: Ejercicios

Last updated
Save as PDF

Page ID: 127669

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

1. Clasifica el ángulo de abajo como agudo, obtuso o derecho.

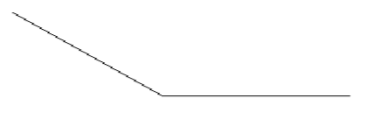
$clipboard_ea48ccb13e941befbd2514bbc79d4cc9b.png$

2. Clasifica el ángulo de abajo como agudo, obtuso o derecho.

$clipboard_e235838468eb6c298b4ad1aa77c0ee428.png$

3. Clasificar el ángulo mostrado como Agudo, Obtuso o Derecho

$clipboard_ebc186a3bcf36db228d1c241ee08a2491.png$

4. Usa la imagen de abajo para responder las siguientes preguntas. Tenga en cuenta que COD es un ángulo recto.

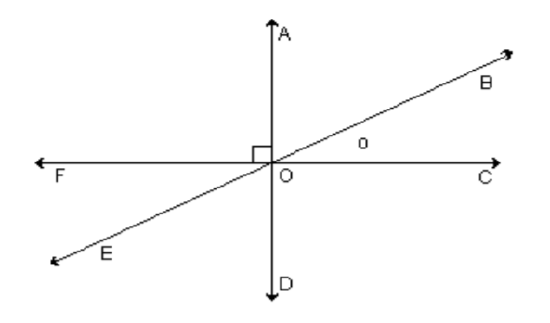
$clipboard_e6387442895240094d68bc05f07439e3f.png$

a) ¿Qué ángulo es complementario a BOC?

b) ¿Qué ángulo es complementario a BOC?

c) ¿Cuál es la medida de EOf?

d) ¿Cuál es la medida de AOE?

e) ¿Cuál es la medida de BOF?

5. Encuentra la medida de ángulo desconocida.

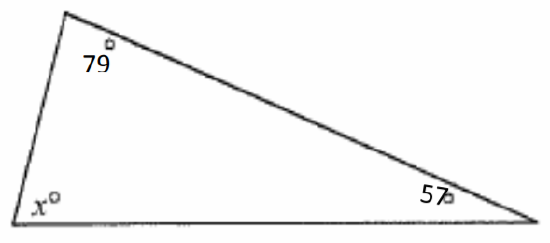
$clipboard_e7c47560535ebea783537bc5c2b4a87b6.png$

6. Encuentra la medida de ángulo desconocida.

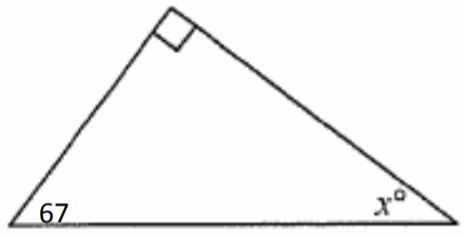
$clipboard_e96ad887a484844449f3c3fb2bb87b2d6.png$

7. Encuentra la medida de ángulo desconocida.

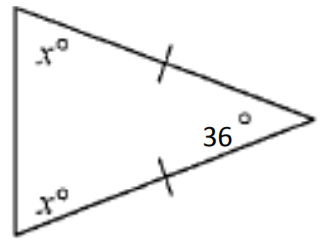
$clipboard_e52a2458dda7a98fb443dcd0c7fc72b2c.png$

8. Encuentra la medida de ángulo desconocida.

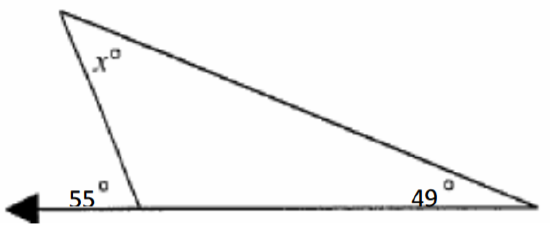
$clipboard_e2e0e98562bd4605cb192192ffda31863.png$

9. Encuentra las medidas de ángulo desconocidas.

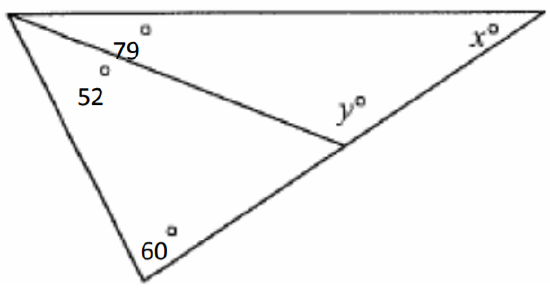
$clipboard_e7f07e49345e1049790c529a2a443aca0.png$

10. Encuentra la medida de ángulo desconocida.

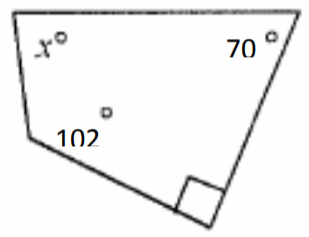
$clipboard_ef1763d273ab3d9f5a1b5d1981dcb6454.png$

11. Encuentra la longitud de la hipotenusa del triángulo rectángulo dado que se muestra a continuación. Redondear a dos decimales.

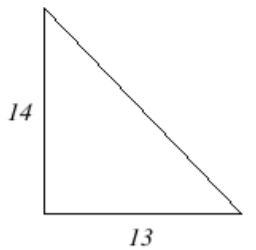
$clipboard_e140963f309a15b859842e57f7b2232ce.png$

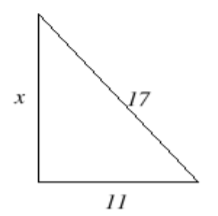
12. Encuentra la longitud de la pierna$x$. Ingresa el valor exacto, no una aproximación decimal.

$clipboard_e56fe15ceef9a1fc945f9a13b74cc303a.png$

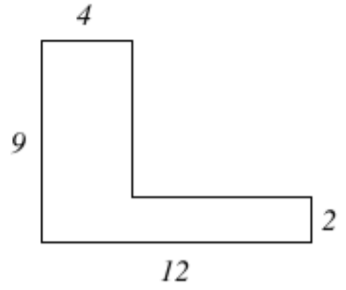
13. Encuentra el perímetro de la figura que se muestra a continuación.

$clipboard_e4aefdfbeb68951c9330644097190bb28.png$

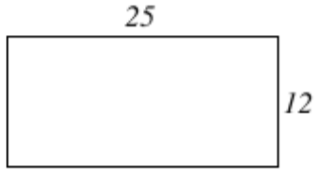
14. Encuentra el perímetro del rectángulo que se muestra a continuación.

$clipboard_e56c02341f1a23097a7ef27fb8ab287bd.png$

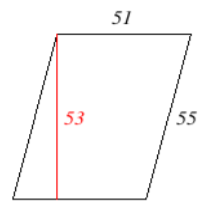
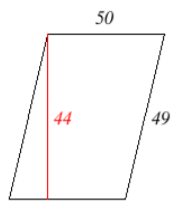
15. Encuentra el perímetro del paralelogramo que se muestra a continuación.

$clipboard_eee5ffb951d769773aa62a1a289600ba0.png$

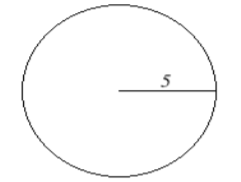
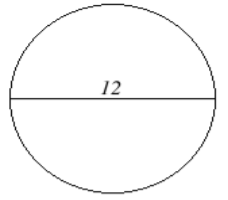
16. Encuentra la circunferencia del círculo que se muestra a continuación. Redondee su respuesta a la centésima más cercana.

$clipboard_e11b3602b9f83f1d21bf3f12d984a2f69.png$

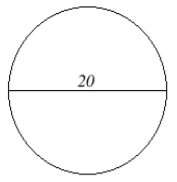
17. Encuentra la circunferencia del círculo que se muestra a continuación. Redondee su respuesta a la centésima más cercana.

$clipboard_e9c52cbd8dc39d1ab1c113968e5bb5dce.png$

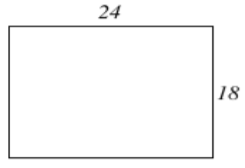
18. Encuentra el área del rectángulo que se muestra a continuación.

$clipboard_ef3cfdf2bf62e1b71b5bfb83430037f13.png$

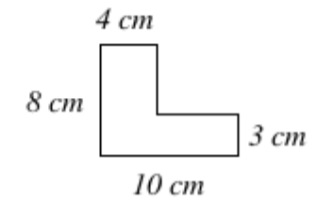
19. Encuentra el área de la figura que se muestra a continuación e indica las unidades correctas.

$clipboard_e82856fe51e9b0790ce910f6df9258272.png$

20. Encuentra el área del paralelogramo que se muestra a continuación.

$clipboard_ee5fe00dae28c99bc4a18207e5a70499d.png$

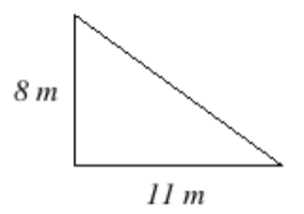
21. El área de un triángulo se puede encontrar usando la fórmula:$\text{Area } = \dfrac{1}{2} \cdot \text{base} \cdot \text{height}$. Encuentra el área del triángulo que se muestra a continuación, donde las medidas se dan en metros (m).

$clipboard_e878643b7bbd30f45e5bb56cd27e2bcf0.png$

22. Encuentra el área del círculo que se muestra a continuación. Redondee su respuesta a la centésima más cercana.

$clipboard_e1b68fe322566ffc2f5c28b62cdc356b5.png$

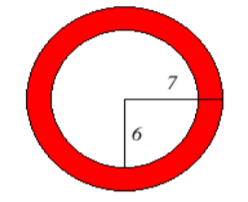
23. Encuentra el área del área sombreada. Redondee su respuesta a la décima más cercana.

$clipboard_e7453e7fbef849482225c4a3610761329.png$

24. Haga coincidir la fórmula para cada volumen con la figura a la que se aplique.

Figura Volumen

________ Cilindro Circular Derecho A.$V = \pi r^2 h$

________ Rectangular Sólido B.$V = \dfrac{4}{3} \pi r^3$

________ Esfera C.$V = l$

25. El volumen de un cilindro con altura$h$ y radio se$r$ puede encontrar usando la fórmula$V = \pi r^2 h$.

Esboce un cilindro con$7$ pies de radio y$4$ pies de altura, luego busque el volumen y seleccione las unidades correctas. Redondee su respuesta a la décima más cercana.

26. El volumen de un cono con altura$h$ y radio se$r$ puede encontrar usando la fórmula$V = \dfrac{1}{3} \pi r^2 h$.

Esboza un cono con$9$ pies de radio y$3$ pies de altura, luego encuentra el volumen y selecciona las unidades correctas. Redondee su respuesta a la décima más cercana.

27. Una pelota deportiva tiene un diámetro de$26 \text{ cm}$. Encuentra el volumen de la bola y selecciona las unidades correctas. Redondee su respuesta a 2 decimales.

Search

Text Color

Text Size

Margin Size

Font Type