18.3: Ecuaciones
- Page ID
- 127715
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Ecuaciones
Una ecuación es una declaración de que dos expresiones algebraicas son iguales
Una ecuación se compone de tres partes.
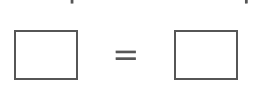
Cada una de las casillas representa una expresión algebraica. Una ecuación consiste en dos expresiones separadas por un signo igual. El signo igual hace la afirmación de que las dos expresiones son equivalentes, es decir, representan el mismo valor. Por ejemplo:
\(f = 32a\)
La ecuación expresa la relación entre las variables\(f\) y\(a\). Afirma que el valor de\(f\) es siempre\(32\) veces el de\(a\).
\(y = 6x + 8\)
La ecuación expresa la relación entre las variables\(x\) y\(y\). Afirma que el valor de\(y\) es siempre\(8\) más que\(6\) veces el valor de\(x\).
Evaluación Numérica
La evaluación numérica es el proceso de determinar un valor sustituyendo números por letras.
Fórmulas
En diversas áreas (negocios, estadística, física, química, astronomía, sociología, psicología, etc.), las ecuaciones particulares ocurren con bastante frecuencia. Tales ecuaciones se llaman fórmulas. La evaluación numérica se utiliza frecuentemente con fórmulas.
Conjunto de Muestras A
\(f = 32a\). Determinar el valor de\(f\) es\(a = 2\)
\(f = 32(2)\). Reemplazar\(a\) por\(2\).
\( = 64\)
\(p = \dfrac{10,000}{v}\).
Esta ecuación química expresa la relación entre la presión\(p\) de un gas y el volumen\(v\) de un gas.
Determinar el valor de\(p\) if\(v = 500\).
\(p = \dfrac{10,000}{500}\)Reemplazar\(v\) por\(500\)
\(z = \dfrac{x-u}{s}\).
Esta ecuación estadística expresa la relación entre las variables\(z, x, u\), y\(s\). Determinar el valor de\(z\) is\(x = 41\),\(u = 45\), y\(s = 1.3\). Redondear a dos decimales.
\(\begin{aligned} z &=\dfrac{41-45}{1.3} \\ &=\dfrac{-4}{1.3} \\ &=-3.08 \end{aligned}\)
\(p = 5w^3 + w^2 - w - 1\).
Esta ecuación expresa la relación entre\(p\) y\(w\). Determinar el valor de\(p\) if\(w = 5\).
\(\begin{aligned} p &=5(5)^{3}+(5)^{2}-(5)-1 \\ &=5(125)+25-(5)-1 \\ &=625+25-5-1 \\ &=644 \end{aligned}\)
Conjunto de práctica A
\(f = 32a\). Determinar el valor de\(f\) if\(a = 6\).
- Contestar
-
\(192\)
\(p = \dfrac{10,000}{v}\). Determinar el valor de\(p\) is\(v = 250\).
- Contestar
-
\(40\)
\(F = \dfrac{9}{5}C + 32\). Determinar el valor de\(F\) si\(C = 10\)
- Contestar
-
\(50\)
\(y = -9x - 14\). Determinar el valor de\(y\) if\(x = -3\).
- Contestar
-
\(13\)
\(m = 5p^3 - 2p + 7\). Determinar el valor de\(m\) if\(p = -2\).
- Contestar
-
\(-29\)
Ejercicios
Para los siguientes problemas, observar las ecuaciones y exponer la relación que se está expresando.
\(x = 6y\)
- Contestar
-
El valor de\(x\) es igual a seis veces el valor de\(y\).
\(y = x + 4\)
\(e = g - 9\)
- Contestar
-
\(e\)es igual a\(9\) menos que el valor de\(g\).
\(y = x - 7\)
\(3t = 6s\)
- Contestar
-
El valor de tres veces\(t\) es igual a seis veces\(s\).
\(u = v^5\)
\(r = \dfrac{2}{9}s\)
- Contestar
-
El valor de\(r\) es igual a dos novena veces el valor de\(s\).
\(b = \dfrac{3}{4}a\)
\(f = 0.97k + 55\)
- Contestar
-
El valor de\(f\) es igual a\(55\) más de\(\dfrac{97}{100}\) veces el valor de\(k\).
\(w = 4z^3 - 21\)
\(q^2 = 9x^8 + 2y\)
- Contestar
-
El valor de\(q^2\) es igual a nueve veces el valor de\(x^8\) más dos veces el valor de\(y\).
\(I = m^2qb^5 + 3.115p\)
Utilizar la evaluación numérica de las ecuaciones para los siguientes problemas.
Geometría (circunferencia de un círculo)
\(C = 2\pi r\). Buscar\(C\) si\(\pi\) se aproxima por\(3.14\) y\(r = 5\)
- Contestar
-
\(31.4\)
Geometría (área de un rectángulo)
\(A = lw\). Encuentra\(A\) si\(l = 15\) y\(w = 9\).
Electricidad (corriente en un circuito)
\(I = \dfrac{E}{R}\). Encuentra\(I\) si\(E = 21\) y\(R = 7\).
- Contestar
-
\(3\)
Electricidad (corriente en un circuito)
\(I = \dfrac{E}{R}\). Encuentra\(I\) si\(E = 106\) y\(R = 8\).
Negocios (interés simple)
\(I = prt\). Encuentra\(I\) si\(p = 3000\),\(r = 0.12\), y\(t = 1\).
- Contestar
-
\(360\)
Negocios (interés simple)
\(I = prt\). Encuentra\(I\) si\(p = 250\),\(r = 0.07\), y\(t = 6\).
Geometría (área de un paralelogramo)
\(A = bh\). Encuentra\(A\) si\(b = 16\) y\(h = 6\).
- Contestar
-
\(96\)
Geometría (área de un triángulo)
\(A = \dfrac{1}{2}bh\). Encuentra\(A\) si\(b = 25\) y\(h = 10\).
Geometría (perímetro de un rectángulo)
\(P = 2l + 2w\). Encuentra\(P\) si\(l = 3\) y\(w = 1\).
- Contestar
-
\(8\)
Geometría (perímetro de un rectángulo)
\(P = 2l + 2w\). Encuentra\(P\) si\(l = 74\) y\(w = 16\).
Geometría (perímetro de un rectángulo)
\(P = 2l + 2w\). Encuentra\(P\) si\(l = 8\dfrac{1}{4}\) y\(w = 12\dfrac{8}{9}\).
- Contestar
-
\(42\dfrac{5}{18}\)
Física (fuerza)
\(F = 32m\). Encuentra\(F\) si\(m = 6\).
Física (fuerza)
\(F = 32m\). Encuentra\(F\) si\(m = 14\).
- Contestar
-
\(448\)
Física (fuerza)
\(F = 32m\). Encuentra\(F\) si\(m = 14\).
- Responder
-
\(448\)
Física (fuerza)
\(F = 32m\). Encuentra\(F\) si\(m = 6.42\).
- Responder
-
\(205.44\)
Física (momentum)
\(p = mv\). Averiguar\(p\) si\(m = 18\) y\(v = 5\)
Física (momentum)
\(p = mv\). Averiguar\(p\) si\(m = 44\) y\(v = 9\)
- Responder
-
\(396\).
Física (momentum)
\(p = mv\). Averiguar\(p\) si\(m = 9.18\) y\(v = 16.5\)
Física (energía)
\(E = \dfrac{1}{2}mv^2\). Encuentra\(E\) si\(m = 12\) y\(v = 5\).
- Responder
-
\(150\)
Física (energía)
\(E = \dfrac{1}{2}mv^2\). Encuentra\(E\) si\(m = 8\) y\(v = 15\).
Física (energía)
\(E = \dfrac{1}{2}mv^2\). Encuentra\(E\) si\(m = 24.02\) y\(v = 7\).
- Responder
-
\(588.49\)
Astronomía (ley de Kepler del movimiento planetario)
\(P^2 = ka^3\). Encuentra\(P^2\) si\(k = 1\) y\(a = 4\).
Astronomía (ley de Kepler del movimiento planetario)
\(P^2 = ka^3\). Encuentra\(P^2\) si\(k = 8\) y\(a = 31\).
- Responder
-
238,328
Astronomía (ley de Kepler del movimiento planetario)
\(P^2 = ka^3\). Encuentra\(P^2\) si\(k = 4\) y\(a = 5.1\).
Astronomía (ley de Kepler del movimiento planetario)
\(P^2 = ka^3\). Encuentra\(P^2\) si\(k = 53.7\) y\(a = 0.7\).
- Responder
-
\(18.4191\)
Negocios (ganancias, ingresos y costos)
\(P = R - C\). Encuentra\(P\) si\(R = 3100\) y\(C = 2500\).
Negocios (ganancias, ingresos y costos)
\(P = R - C\). Encuentra\(P\) si\(R = 4240\) y\(C = 3590\).
- Responder
-
\(650\)
Geometría (área de un círculo)
\(A = \pi r^2\). Encuentra\(A\) si\(\pi\) es aproximadamente\(3.14\) y\(r = 3\).
Geometría (área de un círculo)
\(A = \pi r^2\). Encuentra\(A\) si\(\pi\) es aproximadamente\(3.14\) y\(r = 11\).
- Responder
-
\(379.94\)
\(t = 21x + 6\). Encuentra\(t\) si\(x = 3\)
\(t = 21x + 6\). Encuentra\(t\) si\(x = 97\)
- Responder
-
\(2,043\)
\(E = mc^2\). Encuentra\(E\) si\(m = 2\) y\(c = 186,000\).
\(E = mc^2\). Encuentra\(E\) si\(m = 5\) y\(c = 186,000\).
- Responder
-
\(1.7298 \times 10^{11}\).
Un objeto viaja en una línea horizontal. La distancia que recorre se representa\(d\) y se mide en metros. La ecuación que relaciona el tiempo de viaje\(t\), y la distancia de viaje\(d\),, es
\(d=t2−4t+20\)
Determinar la distancia recorrida por el objeto si ha estado en movimiento durante\(6\) segundos.
En medicina, existen varias reglas generales utilizadas por los médicos para determinar la dosis de un niño,\(D_c\), de un medicamento en particular. Una de esas reglas, la Regla de Young, relaciona la dosis de un medicamento para un niño con la dosis de un adulto de ese medicamento,\(D_a\). La regla de Young es
\(D_c = \dfrac{t}{t+12} \cdot D_a\)
donde\(t\) es la edad del niño en años. ¿Qué se debe administrar a un niño de 8 años si la dosis correspondiente para adultos es de 15 unidades?
- Responder
-
6 unidades
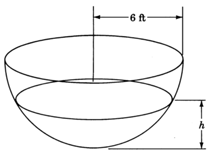
Un tanque de agua hemisférico de\(6\) pies de radio tiene agua goteando en él. La ecuación que relaciona el volumen\(V\),, de agua en el tanque en cualquier momento es\(V=6\pi h^2−\pi 3h^3\), donde\(h\) representa la profundidad del agua. Utilizando\(3.14\) para aproximar el número irracional\(\pi\), determinar el volumen de agua en el tanque cuando la profundidad del agua es\(3\) pies.
La ecuación\(W=3.51L−192\) ha sido establecida por la Comisión Ballenera Internacional para relacionar el peso,\(W\) (en toneladas largas), de una ballena azul madura con su longitud,\(L\) (en pies). La ecuación sólo se usa cuando\(L \ge 70\). Cuando las ballenas
\(0<L<70\)
azules son consideradas inmaduras. Al nacer, una ballena azul mide aproximadamente\(24\) pies de largo. Determinar el peso de una ballena azul que mide\(83\) pies de longitud.
- Responder
-
\(99.33\)toneladas
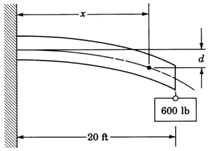
Existe una relación entre la longitud de una viga en voladizo y la cantidad que se desvía cuando se fija un peso a su extremo. Si una viga en voladizo de\(20\) pies de largo tiene un peso en\(600\) libras unido a su extremo, la ecuación que relaciona la longitud de la viga y la cantidad de deflexión es
\(d = \dfrac{60x^2-x^3}{16,000}\)
donde\(d\) es la cantidad de deflexión medida en pulgadas y\(x\) es la longitud desde la parte soportada de la viga hasta algún punto de la viga en el que se mide la cantidad de deflexión. Encuentra la cantidad de deflexión de los\(17\) pies de la viga desde el extremo soportado.
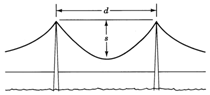
Existe una relación entre la longitud de un cable de puente colgante que se asegura entre dos soportes verticales y la cantidad de pandeo del cable. Si representamos la longitud del cable por\(c\), la distancia horizontal entre los soportes verticales por\(d\), y la cantidad de pandeo por\(s\), la ecuación es\(c=d + \dfrac{8s^2}{3d} - \dfrac{32s^4}{5d^3}\). Si la distancia horizontal entre los dos soportes verticales es\(190\) pies y la cantidad de pandeo en un cable que está suspendido entre los dos soportes es\(20\) pies, ¿cuál es la longitud del cable?
- Responder
-
\(195.46474\)
Ejercicios para revisión
Simplificar\((4x^3y^8)(3x^2y)\)
Simplificar\(-|-8|\)
- Responder
-
\(-8\)
Encuentra el valor de\(4^{-2} \cdot 8^2 - 3^2\).
Para la expresión\(5(a + b) + 2x^2\), escribir el número de términos que aparecen y luego escribir los términos ellos mismos.
- Responder
-
\(2; 5(a + b), 2x^2\)
¿Cuántos\(xy^3\) hay adentro\(5x^2y^5\)?


