4.8: Antiderivatives
( \newcommand{\kernel}{\mathrm{null}\,}\)
At this point, we have seen how to calculate derivatives of many functions and have been introduced to a variety of their applications. We now ask a question that turns this process around: Given a function
We answer the first part of this question by defining antiderivatives. The antiderivative of a function
The Reverse of Differentiation
At this point, we know how to find derivatives of various functions. We now ask the opposite question. Given a function
Definition: Antiderivative
A function
for all
Consider the function
General Form of an Antiderivative
Let
- for each constant
- if
In other words, the most general form of the antiderivative of
We use this fact and our knowledge of derivatives to find all the antiderivatives for several functions.
Example
For each of the following functions, find all antiderivatives.
Solution:
a. Because
then
b. Let
For
Therefore,
Thus,
c. We have
so
d. Since
then
Exercise
Find all antiderivatives of
- Hint
-
What function has a derivative of
- Answer
-
Indefinite Integrals
We now look at the formal notation used to represent antiderivatives and examine some of their properties. These properties allow us to find antiderivatives of more complicated functions. Given a function
The symbol
Definition: Indefinite Integrals
Given a function
is the most general antiderivative of
The expression
Given the terminology introduced in this definition, the act of finding the antiderivatives of a function
For a function
The collection of all functions of the form
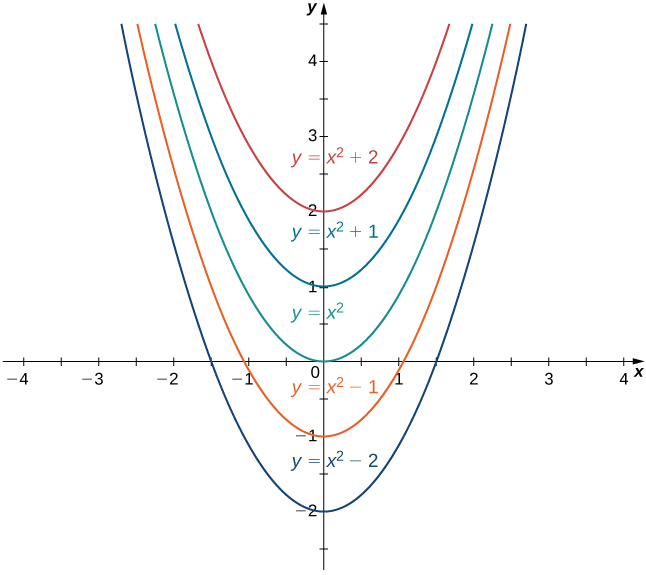
Figure
For some functions, evaluating indefinite integrals follows directly from properties of derivatives. For example, for
which comes directly from
This fact is known as the power rule for integrals.
Power Rule for Integrals
For
Evaluating indefinite integrals for some other functions is also a straightforward calculation. The following table lists the indefinite integrals for several common functions. A more complete list appears in Appendix B.
| Differentiation Formula | Indefinite Integral |
|---|---|
From the definition of indefinite integral of
if and only if
it is important to check whether this statement is correct by verifying that
Example
Each of the following statements is of the form
Solution:
a. Since
the statement
is correct.
Note that we are verifying an indefinite integral for a sum. Furthermore,
b. Using the product rule, we see that
Therefore, the statement
is correct.
Note that we are verifying an indefinite integral for a product. The antiderivative xex−ex is not a product of the antiderivatives. Furthermore, the product of antiderivatives,
In general, the product of antiderivatives is not an antiderivative of a product.
Exercise
Verify that
- Hint
-
Calculate
- Answer
-
In Table, we listed the indefinite integrals for many elementary functions. Let’s now turn our attention to evaluating indefinite integrals for more complicated functions. For example, consider finding an antiderivative of a sum
Therefore,
Similarly,
In addition, consider the task of finding an antiderivative of
for any real number
These properties are summarized next.
Properties of Indefinite Integrals
Let
Sums and Differences
Constant Multiples
From this theorem, we can evaluate any integral involving a sum, difference, or constant multiple of functions with antiderivatives that are known. Evaluating integrals involving products, quotients, or compositions is more complicated (see Exampleb. for an example involving an antiderivative of a product.) We look at and address integrals involving these more complicated functions in Introduction to Integration. In the next example, we examine how to use this theorem to calculate the indefinite integrals of several functions.
Example
Evaluate each of the following indefinite integrals:
Solution:
a. Using Note, we can integrate each of the four terms in the integrand separately. We obtain
From the second part of Note, each coefficient can be written in front of the integral sign, which gives
Using the power rule for integrals, we conclude that
b. Rewrite the integrand as
Then, to evaluate the integral, integrate each of these terms separately. Using the power rule, we have
c. Using Note, write the integral as
Then, use the fact that
d. Rewrite the integrand as
Therefore,
Exercise
Evaluate
- Hint
-
Integrate each term in the integrand separately, making use of the power rule.
- Answer
-
Initial-Value Problems
We look at techniques for integrating a large variety of functions involving products, quotients, and compositions later in the text. Here we turn to one common use for antiderivatives that arises often in many applications: solving differential equations.
A differential equation is an equation that relates an unknown function and one or more of its derivatives. The equation
is a simple example of a differential equation. Solving this equation means finding a function
are given by
Sometimes we are interested in determining whether a particular solution curve passes through a certain point
with the additional condition
is an example of an initial-value problem. The condition
and the initial condition
is an example of an initial-value problem. Since the solutions of the differential equation are
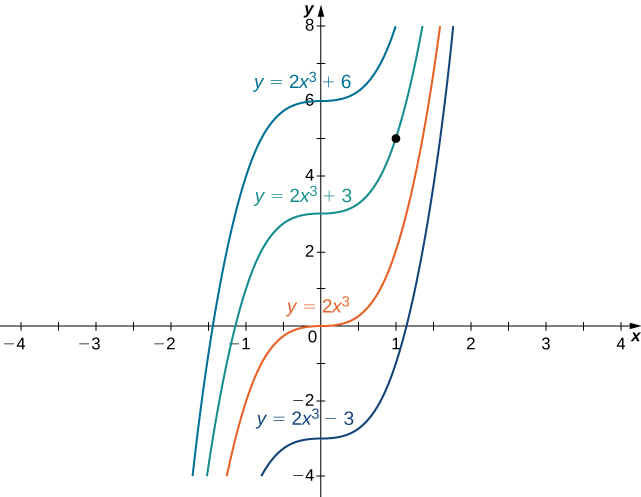
Figure
Example
Solve the initial-value problem
Solution
First we need to solve the differential equation. If
Next we need to look for a solution
The solution of the initial-value problem is
Exercise
Solve the initial value problem
- Hint
-
Find all antiderivatives of
- Answer
-
Initial-value problems arise in many applications. Next we consider a problem in which a driver applies the brakes in a car. We are interested in how long it takes for the car to stop. Recall that the velocity function
Example
A car is traveling at the rate of
- How many seconds elapse before the car stops?
- How far does the car travel during that time?
Solution
a. First we introduce variables for this problem. Let
The car is traveling at a rate of
The acceleration is the derivative of the velocity,
Therefore, we have an initial-value problem to solve:
Integrating, we find that
Since
To find how long it takes for the car to stop, we need to find the time t such that the velocity is zero. Solving
b. To find how far the car travels during this time, we need to find the position of the car after
Integrating, we have
Since
After
Exercise
Suppose the car is traveling at the rate of
- Hint
-
- Answer
-
Key Concepts
- If
- Solving the initial-value problem
- requires us first to find the set of antiderivatives of
Glossary
- antiderivative
- a function
- indefinite integral
- the most general antiderivative of
- initial value problem
- a problem that requires finding a function
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

